Enhancing von Neumann entropy by chaos in spin–orbit entanglement*

Chen-Rong Liu(劉郴榮), Pei Yu(喻佩), Xian-Zhang Chen(陳憲章),Hong-Ya Xu(徐洪亞), Liang Huang(黃亮),?,and Ying-Cheng Lai(來穎誠),3

1School of Physical Science and Technology,and Key Laboratory for Magnetism and Magnetic Materials of MOE,Lanzhou University,Lanzhou 730000,China

2School of Electrical,Computer,and Energy Engineering,Arizona State University,Tempe,AZ 85287,USA

3Department of Physics,Arizona State University,Tempe,AZ 85287,USA

Keywords:spin–orbit entanglement,chaos,von Neumann entropy,spin decoherence

1.Introduction

Quantum entanglement,the intercorrelation among different subsystems or distinct degrees of freedom of a system,is foundational to quantum mechanics and fundamental to quantum information science and technology.[1]From the point of view of quantum–classical correspondence,entanglement has no classical counterpart. However,the nature of the classical dynamics can still have some impact on quantum entanglement.[2–16]While vast knowledge has been accumulated in the field of quantum chaos that studies the manifestations of classical chaos in the corresponding quantum system,[19–21]the interplay between chaos and quantum entanglement remains to be a fundamental and fascinating topic in contemporary physics.[2–16]Typically,entanglement is referred to the intercorrelation among different subsystems,e.g.,between two particles(electrons or photons)of an entangled pair.Meanwhile,the entanglement of distinct degrees of freedom of a single particle has also been discussed and demonstrated experimentally.[7,22–27]The purpose of this paper is to investigate the interplay between chaos and intraparticle quantum entanglement that can be characterized,e.g.,by the von Neumann entropy between the spin and the orbital degrees of freedom of a single electron. This problem is highly relevant to spintronics and spin-based quantum computing/communication technologies.Our finding is that chaos can enhance intra-particle quantum entanglement.

Historically, the concept of quantum entanglement was originated from the Einstein–Podolsky–Rosen (EPR)paradox[28]and Schr?dinger’s cat.[29]The phenomenon of quantum entanglement is counterintuitive as it entails nonlocal properties of physical processes[8,11,30–33]and plays an important role in the foundation of quantum mechanics. Various aspects of quantum entanglement such as characterization,detection,and control have been actively investigated,[32]with significant applications in quantum teleportation,[34]quantum searching algorithms,[35]quantum communication[32,36,37]and computing.[32]

Quantum entanglement is intimately related to the concept of quantum coherence based on the principle of superposition of quantum states.[11,31,38]When a state ψ is composed by two coherent states ψ1and ψ2:ψ=ψ1+ψ2,one haswhere the cross term characterizes the coherence and can be observed through interference.The presence of a detector of certain resolution[11,38]will degrade and even destroy the interference pattern and,consequently,coherence.Remarkably,the detector can generate entanglement between the detecting and the object systems,[8,11,30–32]leading to decoherence of the state of the object systems.[8,11,31,39–42]Indeed,the study of decoherence and entanglement constitutes an important branch of modern quantum mechanics.[8,11,30,33,43–45]

There were some previous studies of the role of classical chaos in entanglement and decoherence.[2,5–8,10–13,17,18]For example, the issue of decoherence in classically chaotic systems was investigated in terms of the Lyapunov exponent,[5,6,10,12]where an implicit relation between the purity or coherence of the quantum state and the Lyapunov exponent was obtained in the semiclassical limit.[12]The exponent was shown[12]to be effectively the decay rate of the degree of coherence,i.e.,chaos is more effective at reducing coherence,suggesting that the nature of the classical dynamics plays a determining role in decoherence,regardless of the environment. The inter-relation between decoherence and entanglement then suggests that chaos might be able to enhance entanglement.[3,4,9,13]For a classically chaotic system,the simultaneous loss of coherence of certain degree of freedom and the gain of its entanglement with other degrees of freedom of the system were demonstrated.[11]In optomechanics,it was shown that complicated nonlinear dynamical behaviors can enhance quantum entanglement.[14]

Our investigation of the interplay between chaos and spin–orbit entanglement was motivated by two considerations.Firstly,manipulating the spin degree of freedom is the base of spintronics(a major class of energy efficient electronics[46,47]),the development of which often relies on a good understanding of spin transport[46–48]in mesoscopic solid state devices such as quantum dots.[49]In the mesoscopic regime,both classical and quantum behaviors are relevant,and previous works showed that different types of classical dynamics can have characteristically different effects on the electronic transport phenomena such as conductance fluctuations.[50–62]Thus,while spin is a quantum variable with no classical counterpart,in mesoscopic systems the nature of classical dynamics would have effects on quantum behaviors that involve spin due to the spin–orbit interaction.[63]Secondly,while there were previous studies on the role of classical chaos in spin transport[63–67]and entanglement between the spin and orbital degrees of freedom,[23,25,31,32,68]the interplay between chaos and intraparticle entanglement has not been investigated.Addressing this issue may lead to insights into spin-based quantum computing or quantum information technologies.

In this paper,we study spin–orbit entanglement in twodimensional mesoscopic systems with a focus on the role of classical chaos in intra-particle entanglement. For simplicity,we study entanglement between the spin and orbital degrees of freedom of an electron in quantum-dot systems that can be chaotic in the classical limit. The underlying physical mechanism for the spin–orbit entanglement is Rashba spin–orbit coupling.[68–75]The two-dimensional quantum dot is chosen to be a cosine cavity whose classical dynamical properties can be controlled by continuously varying its length parameter.[56]To be systematic,we study nine system configurations with various degrees of chaos as characterized by the phase space structure and the maximum Lyapunov exponent. The main finding is that,in the weakly Rashba spin–orbit coupling regime,chaos can significantly enhance the spin–orbit entanglement.Because of the potential role of such intra-particle entanglement in,e.g.,quantum teleportation and communication,[76,77]our result points at the advantage of exploiting classical chaos in these applications.[25,27]

It is worth emphasizing the difference between the present work and our previous works on the role of chaos in spin transport.In particular,in Ref.[67],we studied graphene quantum dots subject to unpolarized injection and examined how chaos can induce spin polarization.In Ref.[63],we considered semiconductor two dimensional electron gas(2DEG)cavities with polarized injection and investigated the circumstances under which classical chaos would preserve or destroy spin polarization. In the present work,we address the role of chaos in spin–orbit entanglement,a kind of entanglement between the internal degrees of freedom of a single particle,which can be exploited to enhance the transmission bandwidth in quantum communication. This type of intraparticle entanglement has been studied but mostly in photonic systems.[7,22–27]In solid state systems,one relevant work[68]treated the interplay among time-reversal symmetry,entanglement,and weak-(anti)localization quantum correction to conductance.While the setting of this work is chaotic quantum dots,the issue of the effect of chaos on intra-particle entanglement is not touched.The results in our present work reveal that chaos is capable of distributing scattering electrons into different transmission channels(transverse modes),leading to an enhancement of the spin–orbit entanglement at the expense of spin polarization.To the best of our knowledge,our work has uncovered the beneficial role of chaos in enhancing intraparticle entanglement.

2.Classical dynamics and Rashba Hamiltonian

We consider two-dimensional mesoscopic quantum dot type of systems. An exemplary system consists of a central cavity(scattering region)and a number of electronic waveguides(or leads)connected to the cavity.To generate a wide range of classical dynamical behaviors,we choose the cavity to have a cosine shape,[56,58,78,79]in which the whole spectrum of classical dynamics from integrable to mixed dynamics and finally to fully developed chaos can be arisen through continuous tuning of a geometric parameter of the system.In particular,the cavity region D is defined by the boundaries x=0,x=L,y=0,and y=W+(M/2)[1?cos(2πx/L)]. To be concrete,we assume there are two leads attached to the cavity:one on the left and the other on the right side.The nature of the classical dynamics is determined by the values of the parameter ratios[56]M/L and W/L.For example,for M/L=0.11 and W/L=0.18,the classical phase space is mixed with the coexistence of Kolmogorov–Arnold–Moser(KAM)tori and chaotic regions. For M/L=0.22 and W/L=0.36,there is fully developed chaos without any stable periodic orbit.

Fig.1.Lyapunov exponent of the chaotic component in the cosine cavity.The dashed curve is the maximal Lyapunov exponent λ1 versus the length L of the cavity.The insets are two representative Poincaré surfaces of section of the closed billiard system without leads attached to it:mixed dynamics for L=1.8μm(upper right)and chaotic dynamics for L=0.5μm(lower left).Altogether nine cases of different values of L are shown:L=0.5,0.55,0.6,0.67,0.8,1.0,1.33,1.5,1.8μm.Other parameters are M=0.15μm and W=0.24μm.

In our simulations,we fix M=0.15μm,W=0.24μm(also the width of the leads),and vary L in the range from 0.5μm to 2.0μm so as to generate classical dynamics with different degrees of chaos.In particular,for a closed cosine billiard system,as the length L is altered,the degree of chaos in the classical dynamics can be modulated in a continuous fashion.There are two aspects in the evolution of chaos:the chaotic component in the phase space that can increase in size(accompanied by a simultaneous decrease in the regular KAM component)and the maximum Lyapunov exponent λ1that can be calculated conveniently in the Birkhoff coordinates.[80]Figure 1 shows λ1versus L and representative phase space structures revealed on the Poincaré surface of section.For the four cases with L ≤0.67,there is fully developed chaos without any stable periodic orbit in the phase space.For the five cases with L ≥0.67,the phase space is mixed.[56]

To activate the Rashba spin–orbit interaction,we apply an electrical field perpendicular to the cavity plane.The Hamiltonian of the system is given by[81]

where σ0is the 2×2 unit matrix,are the Pauli matrices,m*is the electron’s effective mass,and α is the strength of Rashba spin–orbit coupling.The confinement potential isandotherwise.

3.Characterization of spin–orbit entanglement and role of classical chaos in enhancing entanglement

For the open billiard system with leads attached to it,propagating or conducting channels will be activated when the electron Fermi energy εfis larger than the cut-off energy of the dispersion relation.[49]Consider the case of two symmetric leads,one on the left and the other on the right side of the scattering region,where the transport direction is from left to right.Suppose there are a number of channels in the left lead,each associated with spin-up states.The incoming orbital and spin states in the left lead are denoted asand,respectively.The outgoing states are in the right lead.In general,the incoming and outgoing states can be written as[82]

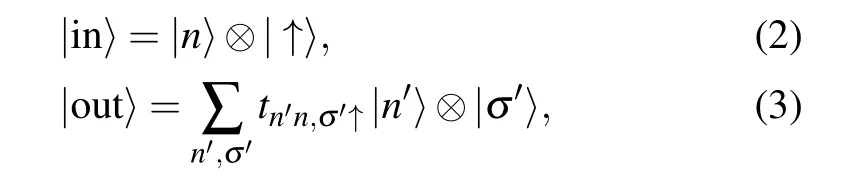
where the square modulus of the expansion coefficientsgives the probability for a spin-up incoming channelfrom the left lead to scatter into a spin-σ′channelstate in the right lead.That is,for any incoming state as defined in Eq.(2),equation(3)gives the corresponding state after scattering.The resulting outgoing state in the right lead is a pure but nonseparable,entangled state.[8,11,30,32,33,41–43]Associated with the outgoing state,the quantum spin and orbital degrees of freedom are thus entangled.[32,41,42,76]

When N channels are activated in the left lead,the incoming state vector can be written as the following superposition state:

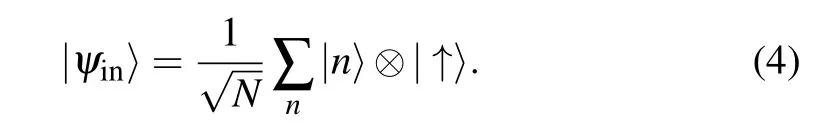
The corresponding state in the right channel after scattering is

With the normalization conditionwe obtain the normalization coefficient as

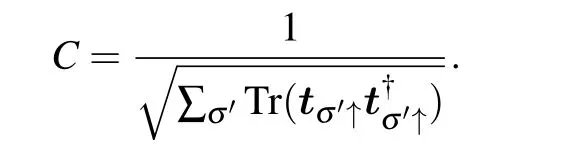
And the outgoing state can be written as

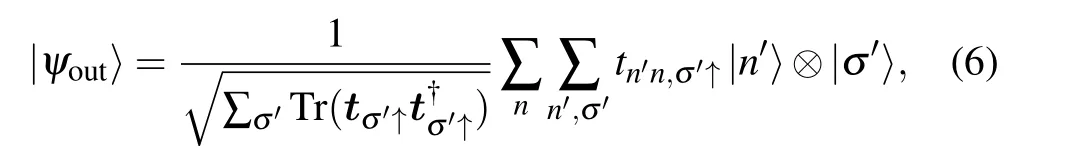
The density matrix associated with the outgoing state is

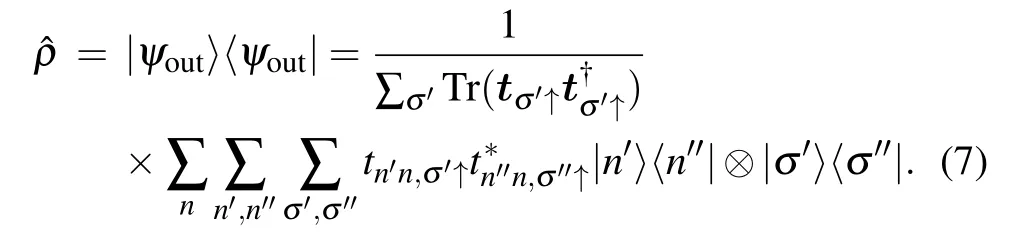
The reduced density matrix for the spin degree of freedom can be obtained by averaging out the total density matrix over the orbital subspace,leading to the spin density matrix that describes the spin subspace from which an observer can get the information about the system including entanglement.[11,30,32,33]Specifically,the spin density matrix is given by[8,81–84]

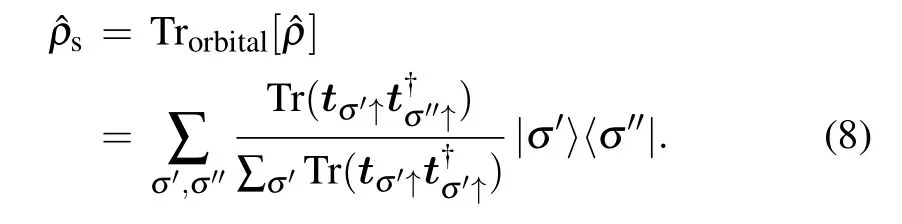
Note that,the reduced spin density matrix no longer corresponds to a pure state,[8,31,83]with which the degree of mixture or reduction in coherence[11]of the remained spin state can be quantified by the puritya measure of the pureness of the state.The amount of spin–orbit entanglement can be quantified by the von Neumann entropy[8,11,30–33]

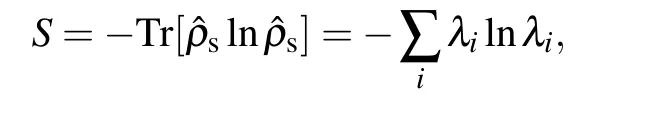
where λi’s are the eigenvalues of the reduced density matrix.

For a spin-1/2 particle,the spin density matrix can be expressed[31,81–83]in terms of the spin polarization vectorThe reduced density matrix in Eq.(8)can thus be expressed as

We then have

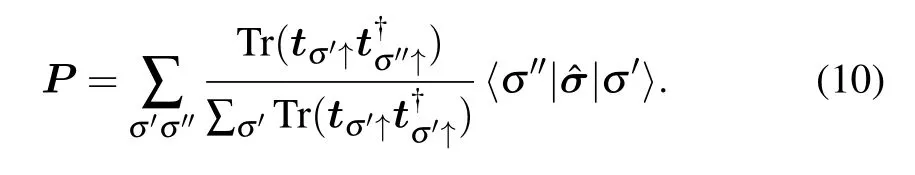
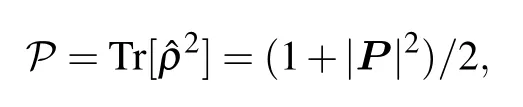
The spin density matrix in Eq.(9)is obtained by tracing over the orbital part of the composite spin-orbit stateBecause the spin density matrix possesses positive eigenvalues(due to the non-negativeness of probability),the positive determinant det[ρs]≥0 leads to the conditionSince the purity associated with Eq.(9)is information about the coherent motion of the spin state is encoded into the rotation ofand the decay of spin coherence will lead to<1.[82,83]This means thatmagnitudecan be effectively an indicator of the purity or the coherence of the spin state.In particular,indicates that this spin state is completely polarized and pure andis a vector on the Bloch sphere,the limit at the other endmeans that this spin state is totally unpolarized.While the intermediate caseindicates that this spin state is partially polarized and incompletely mixed.[11,31]Note that in generalcould be a better indicator of spin coherence as they correspond to the off-diagonal element of the reduced density matrix. While as illustrated in Ref.[82],for spin transport with multi-transmitting modes,the quantitywhich describes the spin polarization of the charge current,could serve the purpose better.Furthermore,we have calculatedthe results are consistent withThus from now on,we shall useas an indicator of spin coherence.

That chaos can enhance spin–orbital entanglement can be argued,heuristically,as follows.The pair of eigenvalues of the spin density matrix can be obtained aswith which the van Neumann entropy can be expressed in terms of the magnitude ofas[86]

The degree of spin–orbit entanglement as characterized by the van Neumann entropy S is thus directly connected withproviding an explicit relation between coherence and entanglement.The orbital degree of freedom is thus responsible for spin decoherence,providing a mechanism through which the spin polarization is reduced.

4.Results

We employ the tight-binding approximation and the recursive scattering matrix method[87–89]to calculate the spinresolved transmission matrixand the spin polarization vectorIn particular,we discretize the scattering region using a square lattice with the nearest hopping energywhere a is the side length of the unit cell.The Rashba spin–orbit interaction strength is tso=α/2a.For convenience,we setso that t0=1 and tsobecomes dimensionless.If the cavity is simply a ribbon,the spin polarization in the perpendicular z direction,denoted as Pz,exhibits periodic oscillations[90–92]with tso.The periodic behavior persists even for a ribbon cavity with rough edges in the regime of weak spin–orbit interaction,although the oscillatory behavior tends to deteriorate as the interaction strength becomes strong.[63]It is thus convenient to normalize tsoby,whereis the specific value of the spin–orbit interaction strength at which the phase of spin polarization ratio Pzchanges by π,e.g.,from spin up prior to entering the cavity to spin down after exiting it.

Figure 2 shows the indicators of spin coherence and the entanglement degree versus the Fermi energy εfand spin–orbit coupling strength tso,where panels(a)and(c)are for a completely chaotic dot as marked byin Fig.1,while panels(b)and(d)display the corresponding results but for the case of mixed classical dynamics specified byin Fig.1.We see that for the fully chaotic cavity,there is a large decrease in coherence as characterized byand simultaneously a marked enhancement of the entanglement degree as quantified by the entropyas compared with the case with mixed dynamics.This suggests that,while both sub-band mixture and spin–orbit coupling reduce the coherence,[82]classical chaos can lead to a larger loss of coherence,as shown explicitly in Fig.2(e).And simultaneously,there is significant enhancement of spin–orbit entanglement by chaos,as shown in Fig.2(f).

Fig.2.Dependence of the indicators of spin coherence and the degree of entanglement on Fermi energy and spin–orbit coupling strength.(a)and(c)Three-dimensional display of the magnitude of the spin polarization vectorand van Neumann entropy S versus the Fermi energy εf and the spin–orbit coupling strength tso for the cavity shape marked asin Fig.1,where the classical dynamics are fully chaotic.(b)and(d)Similar 3D plot but for the case marked as in Fig.1,where the classical dynamics are of the mixed type.(e)The value ofaveraged over a relatively large interval of the Fermi energy versus tso for case (solid curve)and case(dashed curve).(f)The corresponding average value of entropy S versus tso for the cases in(e).Both εf and tso are measured in units of t0,the hopping energy of any pair of nearest sites in the square lattice as a result of discretization of the two-dimensional Schr?dinger equation.

Fig.3.Indicators of spin coherence and the degree of entanglement averaged over the Fermi energy versus the spin–orbit coupling strength.(a)–(d)Averaged magnitude of the polarization vectorand(e)–(h)averaged van Neumann entropy S versus the normalized value tso of spin–orbit interaction strength for four different intervals of energy averaging:[0.016,0.0624],[0.0632,0.140],[0.1408,0.2472],and[0.248,0.3816],corresponding to regimes with one to four transmission modes,respectively.In each panel,the five dot-dashed curves are for mixed dynamics while the four solid curves correspond to chaotic dynamics.

To gain more insights into the phenomenon of enhancement of spin–orbit entanglement by classical chaos,we show in Figs.3(a)–3(d)the value ofaveraged over four different energy intervals,each corresponding to a distinct transport regime. The corresponding behaviors of the entropy S are shown in Figs.3(e)–3(h),respectively. In particular,in Figs.3(a)and 3(e),there is only one activated channel so we haveand S=0 because,in this case,the whole state in Eq.(6)is separable,

where there is no entanglement between the spin and orbital degrees of freedom and consequently,no loss of coherence.In Figs.3(b)–3(d)and 3(f)–3(h),more than one channel are activated.As a result,the value ofis reduced from the unity value,indicating a loss of coherence of the spin state and a simultaneous increase in the entropy. Indeed,insofar as the weak coupling regimeis concerned,the patterns of decrease in coherence and increase in the entanglement degree withas a result of classical chaos persist.If the spin–orbit interaction is too strong,the phenomena of chaos enabled coherence reduction and entanglement enhancement may not hold and the corresponding patterns may even reverse,as in this case chaos can result in enhanced spin sub-band intermixing,but with even bigger fluctuations.[63]That chaos tends to reduce coherence and directly enhances spin–orbit entanglement is consistent with previous results.[8,11,40–42]From the measurement point of view,the loss of coherence is intimately related to entanglement.Actually,the entanglement between the spin and orbital degrees is the direct reason leading to the loss of coherence of the spin state for the class of systems studied here.

5.Conclusion

For a composite quantum bipartite system with subsystems or sub-degrees of freedom,[8,11,30–33]decoherence of a subsystem and entanglement between the subsystems are intimately related.[8,11,30,33]In general,coherence is an important measure characterizing a quantum state that is the superposition of other states.When a detector is present,the quantum properties may be destroyed and the system can approach a state describable by a classical probability distribution. Our work presents an explicit demonstration of this general principle underlying coherence and entanglement in terms of spin and orbital degrees of freedom in mesoscopic electronic/spin systems with distinct types of classical dynamics.In particular,scattering into different orbital subspace leads to a nonseparable state described by a spin density matrix and loss of coherence.The entanglement for this composite system can then be studied based on the coherence of the spin subspace.For this system,reduced coherence and enhanced entanglement are thus two coexisting aspects of the same composite system.

Intuitively,classical chaos can reduce coherence in the spin polarized state through enhanced interaction between different degrees,especially through scattering into different orbital states. A question is then whether chaos can enhance entanglement.While there were previous efforts in this topic,[2,5–8,10–13]we focus on the spin–orbit entanglement,a kind of intra-particle entanglement. Using two-dimensional quantum dot systems with Rashba spin–orbit interactions as a prototypical setting,for which classical dynamics of different degrees of chaos can be readily generated,we calculate the measures of coherence and entanglement for a number of systematic cases and obtain the confirmation that,in the weakly coupling regime,chaos can significantly enhance the spin–orbit entanglement. Our result provides insights into the effect of chaos on orbital–spin hybrid entangled state,which may have potential advantages in enhancing the capacity of quantum communication based on intra-particle entanglement.[76,77,93,94]

Acknowledgment

YCL and HYX are supported by the Pentagon Vannevar Bush Faculty Fellowship program sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering and funded by the Office of Naval Research through Grant No.N00014-16-1-2828.