基于分?jǐn)?shù)階微積分PDλ比例導(dǎo)引的無人機(jī)自動避撞方法

賈耀強(qiáng),孫雪

基于分?jǐn)?shù)階微積分PD比例導(dǎo)引的無人機(jī)自動避撞方法

賈耀強(qiáng),孫雪*

東北林業(yè)大學(xué) 機(jī)電工程學(xué)院, 黑龍江 哈爾濱 150040

為了進(jìn)一步改善無人機(jī)自動避撞方法，本文首先給出了基于碰撞錐檢測方法，然后設(shè)計了分?jǐn)?shù)階微積分PDλ比例導(dǎo)引方法，最后采用簡單迭代法實(shí)現(xiàn)了避撞時間在線估計。仿真結(jié)果表明：該方法參數(shù)較少，計算簡單。相比較傳統(tǒng)比例導(dǎo)引方法而言，該方法過載需求小和較快的收斂速度，且能夠較好地抑制風(fēng)擾動，具有較強(qiáng)抗干擾性。

無人機(jī);自動避撞

隨著無人機(jī)在世界范圍內(nèi)的廣泛應(yīng)用，無人機(jī)的感知與避撞已成為至關(guān)重要的問題。目前，無人機(jī)尚缺乏必要的感知與避撞能力，因此，無法實(shí)現(xiàn)與有人機(jī)共享同一片空域。

在無人機(jī)避撞方面，主要包括導(dǎo)引方法[1]和路徑規(guī)劃方法。由于導(dǎo)引方法計算簡單，實(shí)施性強(qiáng)，研究的主要思路是首先通過碰撞檢測方法檢測可能發(fā)生的碰撞，然后采取合適的避撞方法，在一定的性能指標(biāo)和約束下進(jìn)行避撞飛行。

近年來國內(nèi)外學(xué)者對導(dǎo)引方法進(jìn)行了大量的研究。在無人機(jī)非協(xié)同避撞領(lǐng)域，將導(dǎo)彈攔截控制中的導(dǎo)引方法[2]應(yīng)用于無人機(jī)避撞飛行控制是一類有效的方法，主要有基于比例導(dǎo)引、微分幾何導(dǎo)引、非線性動態(tài)逆導(dǎo)引、智能導(dǎo)引的避撞方法等。傳統(tǒng)的比例導(dǎo)引方法只針對靜態(tài)障礙或者非機(jī)動障礙，當(dāng)存在較大的擾動時，無人機(jī)避撞的安全性能得不到保證。文獻(xiàn)[3]采用最優(yōu)比例導(dǎo)引律實(shí)現(xiàn)無人機(jī)三維避撞并推導(dǎo)出了最優(yōu)比例導(dǎo)引系數(shù)的計算方法。雖然簡化了導(dǎo)引指令的計算，但這類以視線角為基礎(chǔ)的導(dǎo)引指令仍然是非線性的。每一時刻的導(dǎo)引指令需要計算當(dāng)前無人機(jī)飛行狀態(tài)信息，造成避撞時間的估計模型沒有解析解。

避撞時間是無人機(jī)避撞過程中一個非常重要的參數(shù)。當(dāng)采用不同的導(dǎo)引指令時，相對速度跟蹤到碰撞錐邊界的時間不同，導(dǎo)致避撞機(jī)追蹤避撞點(diǎn)的時間也不同。因此需要對避撞時間進(jìn)行估計。通過對避撞時間的限制，可以估計避撞機(jī)需要機(jī)動的范圍。多種改進(jìn)的比例導(dǎo)引方法均依賴于精確的避撞時間估計。

無人機(jī)避撞時間與導(dǎo)彈攔截控制中的攔截時間有相似的地方。在導(dǎo)彈攔截領(lǐng)域，Ghose提出一種精確求解傳統(tǒng)比例導(dǎo)引下的導(dǎo)彈攔截時間[4]。利用存儲的基本解以及多項式系數(shù)通過數(shù)值插值的方法計算不同比例導(dǎo)引系數(shù)下的攔截時間。2016年他又提出了一種統(tǒng)一的適用于傳統(tǒng)比例導(dǎo)引和負(fù)比例導(dǎo)引的時間估計方法，這種估計方法將時間估計分為兩部分，第一部分計算視線角收斂到零的時間，第二部分是攔截器攔截目標(biāo)的時間。

相比較傳統(tǒng)的比例導(dǎo)引方法[5]和PID導(dǎo)引方法，分?jǐn)?shù)階微積分導(dǎo)引方法控制更加靈活，具有更強(qiáng)的抗干擾性。文獻(xiàn)[6]提出一種分?jǐn)?shù)階修正比例導(dǎo)引方法用來解決導(dǎo)彈攔截點(diǎn)過載突變的問題。文獻(xiàn)[7]提出一種基于分?jǐn)?shù)階微積分PDλ比例導(dǎo)引制導(dǎo)律，具有攔截精度高、參數(shù)不敏感、魯棒性強(qiáng)等優(yōu)點(diǎn)。但是以上分?jǐn)?shù)階微積分導(dǎo)引方法均在導(dǎo)彈攔截領(lǐng)域應(yīng)用，并不能直接用于無人機(jī)避撞領(lǐng)域。目前在無人機(jī)避撞領(lǐng)域相關(guān)文獻(xiàn)較少。因此，本文提出一種基于分?jǐn)?shù)階比例微分導(dǎo)引的無人機(jī)自動避撞方法，用來提高避撞系統(tǒng)的靈活性以及魯棒性能，來保證避撞的安全。

1 碰撞檢測方法

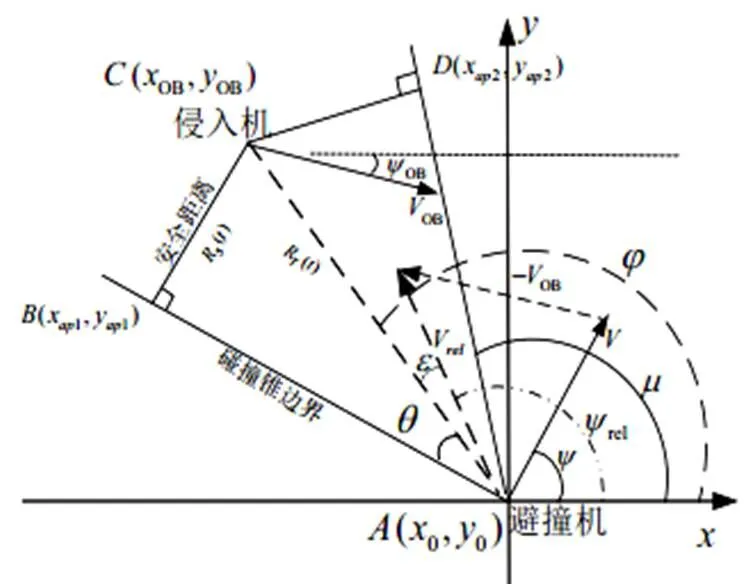
圖1 碰撞錐相對幾何關(guān)系圖

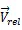
|-Ψ|<(1)

式中，為視線角(LOS)，為避撞機(jī)與侵入機(jī)相對航向角。為碰撞錐的半頂角。因此，只要式(1)滿足，在未來飛行的某一時刻，兩無人機(jī)的間距將小于給定的安全距離，避撞機(jī)與侵入機(jī)可能發(fā)生碰撞，則無人機(jī)需執(zhí)行避撞策略進(jìn)行避撞飛行。

根據(jù)避撞機(jī)與侵入機(jī)相對運(yùn)動以及式(1)可得到無人機(jī)避撞成功的條件為，在避撞機(jī)到達(dá)避撞點(diǎn)B點(diǎn)或者D點(diǎn)之前，式(2)成立。

|-Ψ|≥(2)

避撞機(jī)避撞成功意味著在避撞機(jī)到達(dá)避撞點(diǎn)之前，避撞機(jī)與侵入機(jī)的相對速度向量V至少要跟蹤并收斂到碰撞錐邊界。如果V落在碰撞錐外，避撞一定是成功的。

2 分?jǐn)?shù)階PDλ導(dǎo)引律設(shè)計

2.1 避撞系統(tǒng)總體設(shè)計

當(dāng)檢測到避撞機(jī)與侵入機(jī)可能發(fā)生碰撞之后，避撞機(jī)執(zhí)行合適的避撞策略進(jìn)行避撞。本文主要采用基于分?jǐn)?shù)階PDλ導(dǎo)引律的自動避撞方法。自動避撞系統(tǒng)控制框圖如圖2所示。

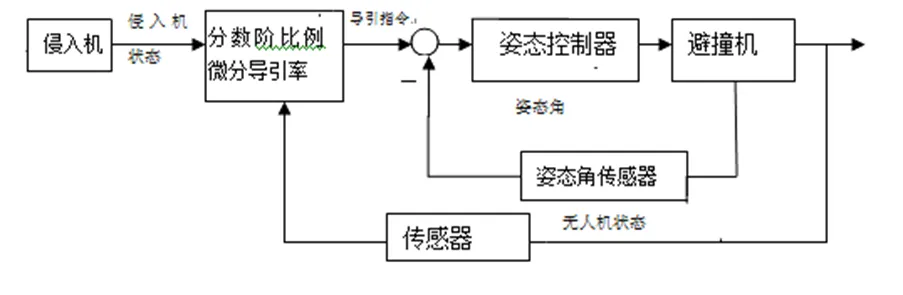
圖2 自動避撞系統(tǒng)控制框圖

圖2中，利用機(jī)載傳感器可以獲得避撞機(jī)與侵入機(jī)的飛行狀態(tài)信息，例如無人機(jī)位置、速度以及航向角等。以這些飛行狀態(tài)信息為輸入，經(jīng)過導(dǎo)引控制環(huán)可得到導(dǎo)引指令，作為姿態(tài)控制環(huán)的給定值，以無人機(jī)橫側(cè)向為例，無人機(jī)得到導(dǎo)引指令繼而得到給定滾轉(zhuǎn)角，通過調(diào)整無人機(jī)航向角實(shí)現(xiàn)協(xié)調(diào)轉(zhuǎn)彎。

2.2 分?jǐn)?shù)階PDλ導(dǎo)引律設(shè)計

首先給出分?jǐn)?shù)階微積分基本操作算子的表達(dá)式：

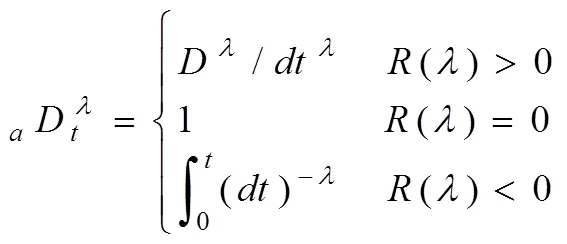
式中，，是微積分的上下限，為微積分的階次。

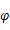
因此，我們定義誤差如下：

=-(5)

其中：

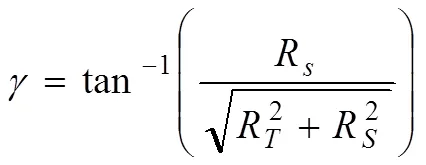
式中，R為兩無人機(jī)間距。采用分?jǐn)?shù)階比例微分控制，可以得到微分方程如下：

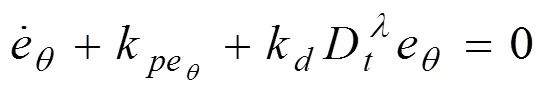
式中，k和k為分?jǐn)?shù)階比例微分導(dǎo)引系數(shù)。e為誤差e的分?jǐn)?shù)階次微分。將式(5)代入式(7)中可得：

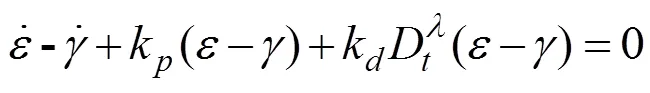
根據(jù)圖1的幾何關(guān)系可得：

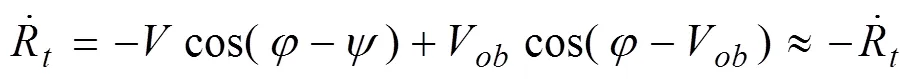
式中，和V分別為避撞機(jī)與侵入機(jī)的速度，和Ψ分別為避撞機(jī)與侵入機(jī)的航向角。

式(9)對時間求導(dǎo)可得：

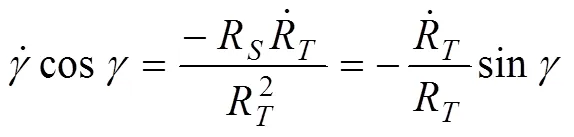
整理式(11)可得：

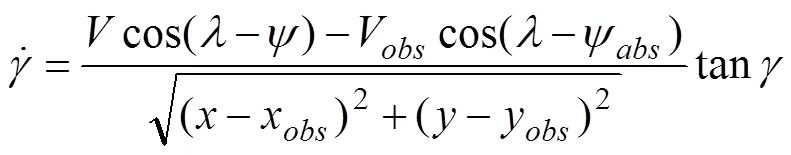
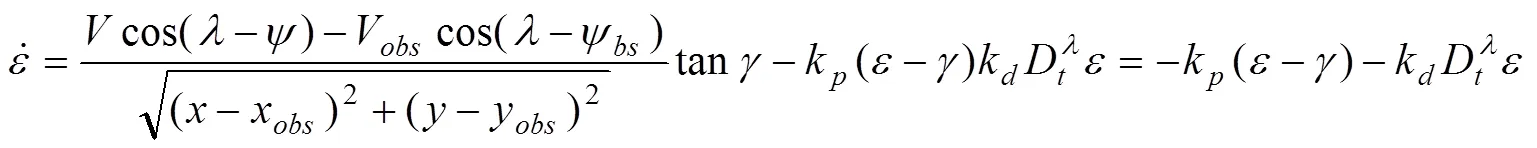
分?jǐn)?shù)階PDλ導(dǎo)引律設(shè)計如下：

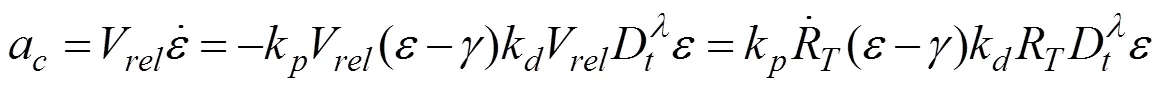
分?jǐn)?shù)階PDλ導(dǎo)引律中包含3個設(shè)計參數(shù)，比例導(dǎo)引系數(shù)k、微分導(dǎo)引系數(shù)k、分?jǐn)?shù)階微分階次。

相比較傳統(tǒng)的比例導(dǎo)引方法和PD型的導(dǎo)引方法，具有較靈活的控制，參數(shù)選擇范圍更廣，參數(shù)適應(yīng)性更強(qiáng)，具有較強(qiáng)的魯棒性。目前，對于分?jǐn)?shù)階PID控制器參數(shù)整定的方法，基于遺傳算法和粒子群算法的參數(shù)整定和優(yōu)化方法已經(jīng)比較成熟[8]，在這里不多加敘述。

3 避撞時間估計

避撞時間是無人機(jī)避撞過程中非常關(guān)鍵的參數(shù)。精確的避撞時間估計可以提高無人機(jī)避撞精確度，減小無人機(jī)機(jī)動范圍。當(dāng)自抗擾導(dǎo)引方法的參數(shù)確定后，避撞時間可以通過以下方法進(jìn)行估計。

控制量簡化為：

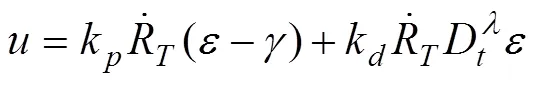
避撞時間分為兩部分：一部分是相對速度跟蹤碰撞錐邊界時間1，一部分是無人機(jī)跟蹤避撞點(diǎn)時間2。無人機(jī)通過改變橫側(cè)向滾轉(zhuǎn)角改變無人機(jī)航向，因此無人機(jī)橫側(cè)向動態(tài)模型可簡化為：

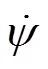
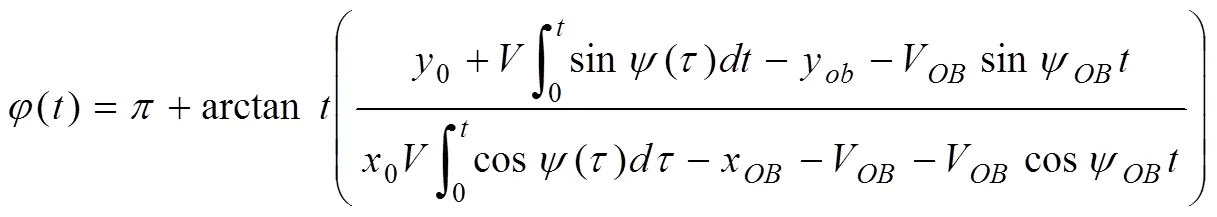
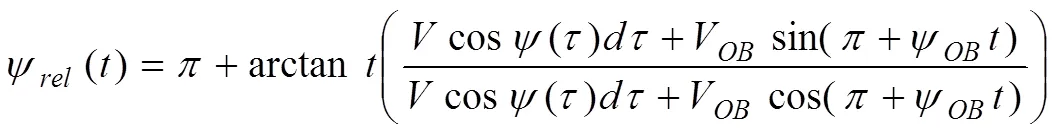
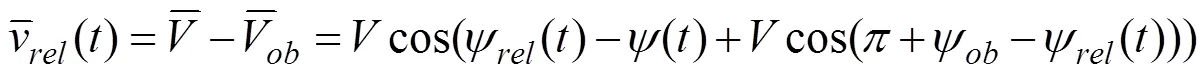
當(dāng)無人機(jī)相對速度跟蹤到碰撞錐邊界時，可得到：

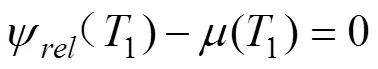
將式(15-19)代入方程式(20)中，通過簡單迭代方法即可求解避撞時1。第二部分無人機(jī)避撞的路徑為保持1時刻航向角勻速飛行的直線。避撞點(diǎn)的坐標(biāo)可通過式(21)求解。

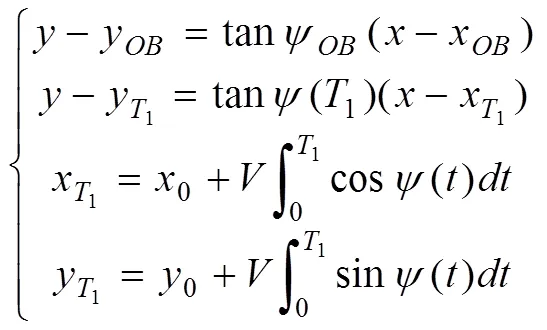
第二部分的避撞時間2可通過式(22)求解：

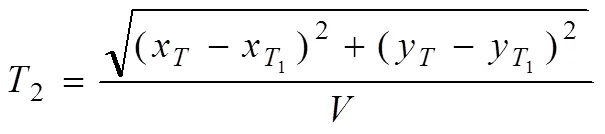
4 仿真驗證

4.1 仿真驗證初始條件

為了驗證提出的分?jǐn)?shù)階PDλ導(dǎo)引方法的性能，本文采用Matlab搭建六自由度無人機(jī)仿真實(shí)驗平臺。以橫側(cè)向無人機(jī)自動避撞為例，當(dāng)式(1)成立時，無人機(jī)開始避撞，避撞機(jī)高度和速度保持恒定，避撞機(jī)通過協(xié)調(diào)轉(zhuǎn)彎來改變避撞機(jī)航向角實(shí)現(xiàn)避撞。

避撞機(jī)副翼和方向舵動態(tài)特性如下：

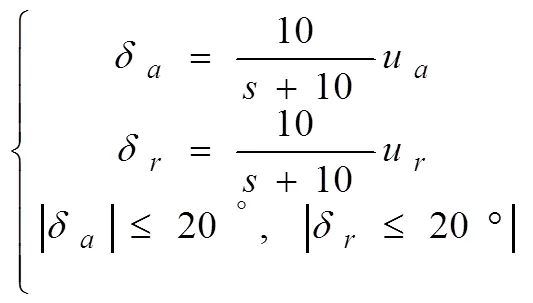
式中，δ和δ分別為副翼和方向舵偏角。μ和μ分別為副翼和方向舵的輸入。

設(shè)定安全距離為R=2 km避撞機(jī)與侵入機(jī)的初始高度為6 km。避撞機(jī)與侵入機(jī)仿真初始條件如表1和2所示。

表1 避撞的初始條件

表2 侵入機(jī)的初始條件

根據(jù)第三部分的避撞時間估計方法可得到兩個案例的避撞估計時間如表3所示。

表3 避撞完成時間估計

4.2 仿真案例

4.2.1 案例一此案例中，避撞機(jī)的速度與侵入機(jī)的速度相同。避撞機(jī)與侵入機(jī)初始航向夾角為5/6。通過和傳統(tǒng)的比例導(dǎo)引避撞方法比較，來驗證分?jǐn)?shù)階PDλ導(dǎo)引方法的性能。導(dǎo)引系數(shù)為k=3.3，k=1，=-1.1。避撞軌跡如圖3所示。

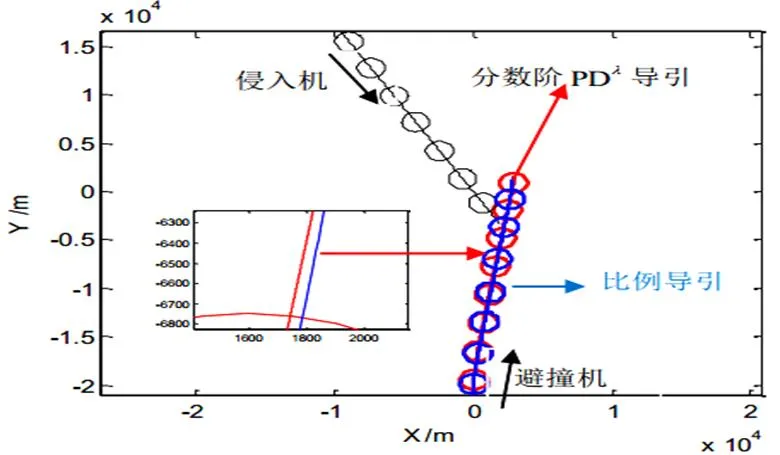
圖3 案例一避撞機(jī)與侵入機(jī)的避撞軌跡

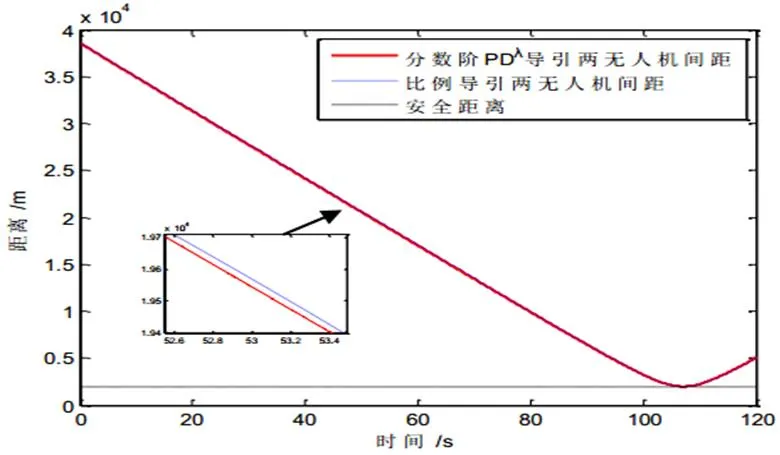
圖4 案例一避撞機(jī)與侵入機(jī)間距

圖3中，在第七個采樣圓時刻附近，兩采樣圓相切。避撞機(jī)與侵入機(jī)的間距到達(dá)最小。兩種導(dǎo)引方法均能避撞成功。采用基于分?jǐn)?shù)階PDλ導(dǎo)引方法的避撞機(jī)機(jī)動范圍要小于傳統(tǒng)比例導(dǎo)引方法的機(jī)動范圍。

從圖4中可以看出，在107 s時，避撞機(jī)與侵入機(jī)間距達(dá)到最小值，等于給定的安全距離。避撞成功。整個避撞過程中，采用基于分?jǐn)?shù)階PDλ導(dǎo)引方法的避撞機(jī)與侵入機(jī)間距始終小于傳統(tǒng)比例導(dǎo)引方法。

圖5中，分?jǐn)?shù)階PDλ導(dǎo)引方法的避撞機(jī)滾轉(zhuǎn)角以及導(dǎo)引指令要小于傳統(tǒng)比例導(dǎo)引方法，過載需求小。而且兩種方法的收斂速度相近。在107 s時避撞完成，與表3中估計的避撞時間104 s誤差為3 s。

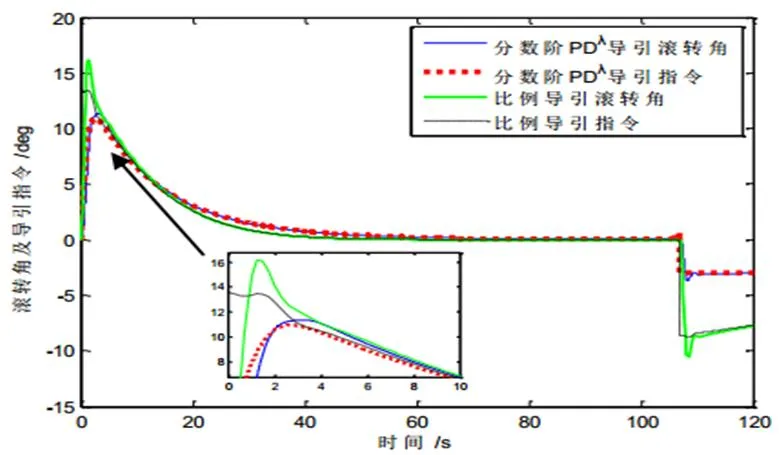
圖5 案例一避撞機(jī)滾轉(zhuǎn)角及導(dǎo)引指令

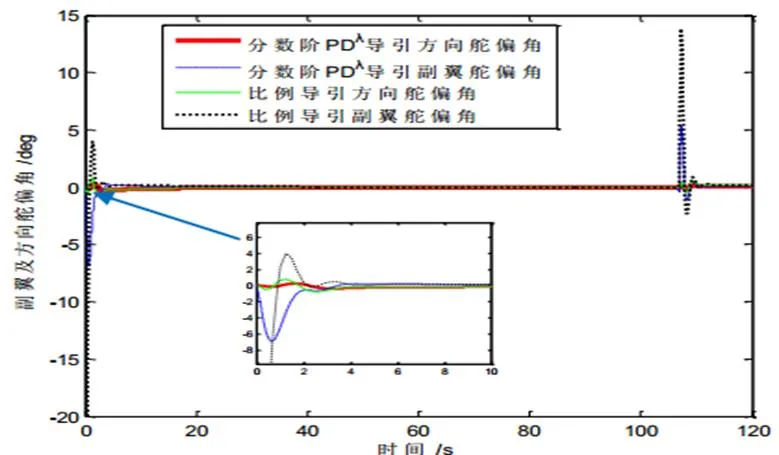
圖6 案例一避撞機(jī)副翼及方向舵偏角

圖6中，兩種方法中的方向舵偏均較小。基于分?jǐn)?shù)階PDλ導(dǎo)引方法的副翼舵偏要明顯小于傳統(tǒng)比例導(dǎo)引方法。兩種導(dǎo)引方法的舵面偏轉(zhuǎn)均小于舵偏的限幅值20°。

4.2.2 案例二案例二中，避撞機(jī)的速度要小于侵入機(jī)的速度。避撞機(jī)與侵入機(jī)初始航向夾角為π/2。在仿真時間30 s加入幅值為20 m/s的常值風(fēng)擾動。避撞軌跡如圖7所示。

圖7中，在第8個采樣圓時刻附近，避撞機(jī)與侵入機(jī)采樣圓相切，避撞機(jī)與侵入機(jī)間距達(dá)到最小值。盡管存在風(fēng)擾動，但同一時刻避撞機(jī)與侵入機(jī)采樣圓并未相交。避撞機(jī)避撞成功。

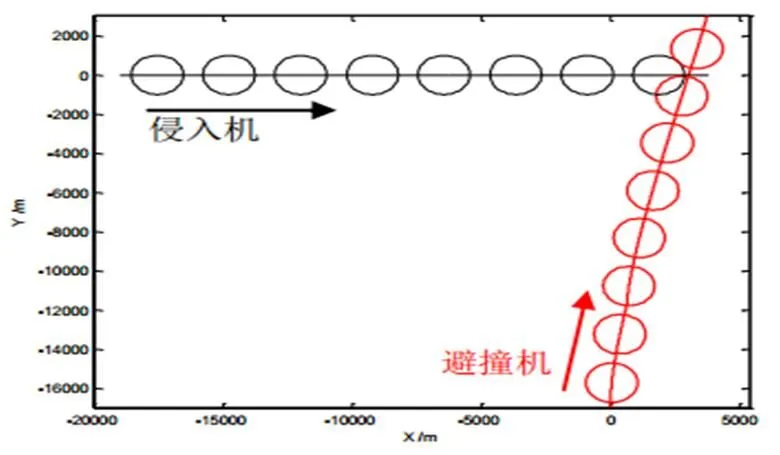
圖7 案例二避撞機(jī)與侵入機(jī)的避撞軌跡

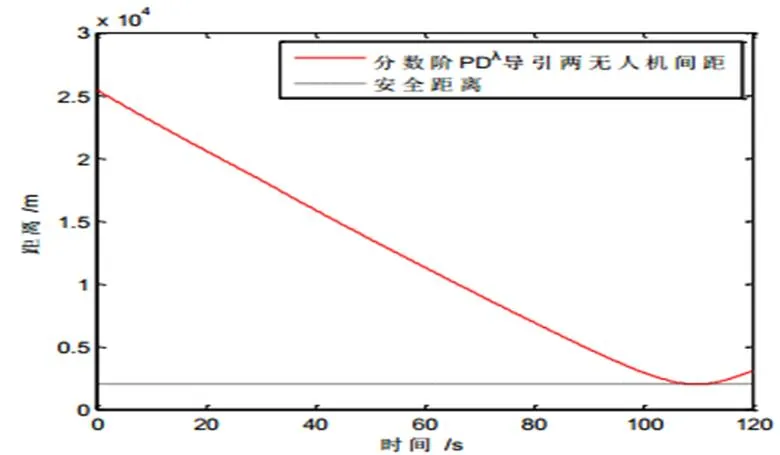
圖8 案例二避撞機(jī)與侵入機(jī)間距

圖8中，在存在風(fēng)擾動的情況下，避撞機(jī)與侵入機(jī)間距始終大于或等于給定的安全距離，避撞機(jī)避撞成功。避撞時間為110 s，與表3中估計的避撞時間110 s誤差為2 s。

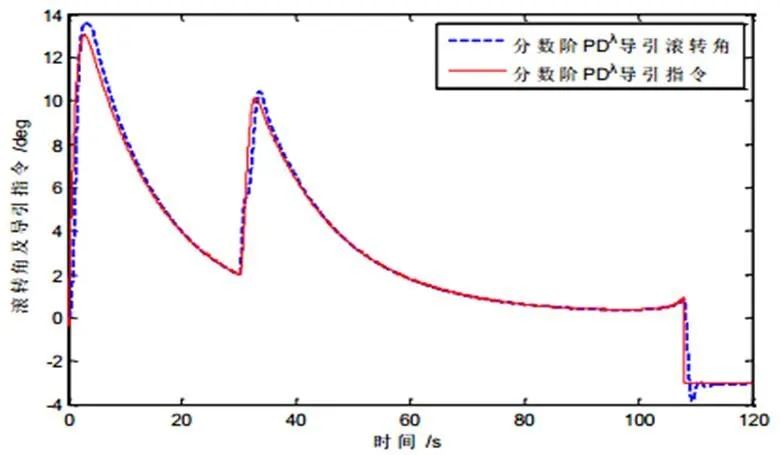
圖9 案例二避撞機(jī)滾轉(zhuǎn)角及導(dǎo)引指令

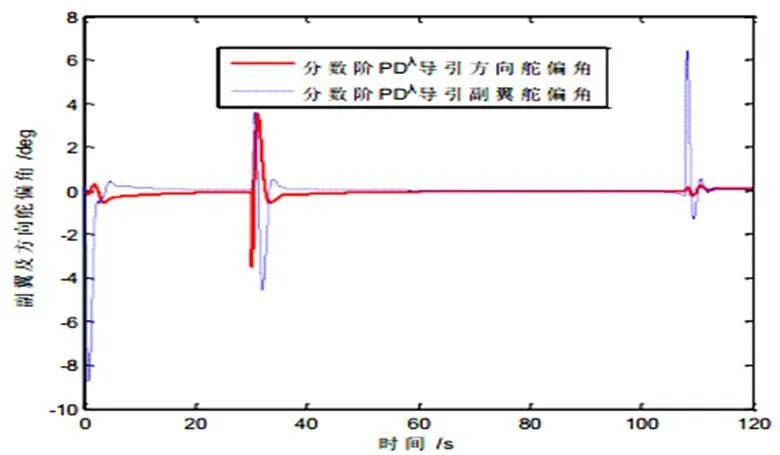
圖10 案例二避撞機(jī)副翼及方向舵偏角

圖9中，由于在30 s時加入常值風(fēng)擾動，根據(jù)分?jǐn)?shù)階PDλ導(dǎo)引方法計算出新的導(dǎo)引指令來抑制風(fēng)擾動。滾轉(zhuǎn)角峰值小于14°滿足無人機(jī)橫向過載要求。

圖10中，副翼舵偏峰值小于9°，明顯小于舵面偏轉(zhuǎn)的限幅值20°。在仿真時間30 s時，由于存在風(fēng)擾動，產(chǎn)生副翼舵面偏轉(zhuǎn)來抑制風(fēng)擾動。

5 結(jié)論

本文提出一種基于分?jǐn)?shù)階PDλ導(dǎo)引的無人機(jī)自動避撞方法并完成了仿真驗證，得到了以下結(jié)論。

（1）該無人機(jī)自動避撞方法所產(chǎn)生的導(dǎo)引指令計算簡單，在多種避撞初始條件下均能避撞成功。利用簡單迭代法實(shí)現(xiàn)了避撞時間的在線估計。

（2）相比較于傳統(tǒng)比例導(dǎo)引方法，分?jǐn)?shù)階PDλ導(dǎo)引具有過載要求小的優(yōu)勢，而且收斂速度相近。通過仿真分析可知該避撞方法具有較強(qiáng)的抗擾性能。能夠很好的應(yīng)對風(fēng)力干擾等擾動。

[1] Yu X, Zhang Y. Sense and avoid technologies with applications to unmanned aircraft systems: review and prospects[J]. Progress in Aerospace Sciences, 2015,74:152-166

[2] 呂永佳,張合新,李正文,等.自抗擾三維最優(yōu)比例滑模導(dǎo)引律設(shè)計[J].科學(xué)技術(shù)與工程,2011,11(12):2814-2818

[3] Han SC, Bang H, Yoo CS. Proportional navigation-based collision avoidance for UAVs[J]. International Journal of Control, Automation and Systems, 2009,7(4):553-565

[4] Dhananjay N, Ghose D. Accurate time-to-go estimation for proportional navigation guidance[J]. Journal of Guidance, Control, and Dynamics, 2014,37(4):1378-1383

[5] 葉繼坤,韋道知,李炯,等.基于分?jǐn)?shù)階微積分理論的新型三維末制導(dǎo)律[J].固體火箭技術(shù),2016(3):428-435

[6] 朱竹婷,廖增,彭程,等.一種分?jǐn)?shù)階修正比例導(dǎo)引律[J].控制理論與應(yīng)用,2012,29(7):945-948

[7] 王飛,雷虎民.基于分?jǐn)?shù)階微積分PDλ比例導(dǎo)引制導(dǎo)規(guī)律[J].控制理論與應(yīng)用,2010,27(1):126-130

[8] 閆璽.分?jǐn)?shù)階PID控制器及其參數(shù)整定的研究[D].西安:西安理工大學(xué),2014

A Method Auto-avoiding UAV Collision Based on Fractional Calculus PDλGuidance

JIA Yao-qiang, SUN Xue*

150040,

To further improve a method auto-avoiding UAV collision, firstly the detection method based on the collision cone was proposed, and then the fractional calculus PDλguidance method was designed, at last collision time estimation on line got by a simple iterative method. The simulation result showed the method had fewer parameters and a simple calculation. Compared with the traditional proportional guidance method, it required a small overload and faster convergence speed, and was able to control a wind disturbance and had a stronger anti-interference.

Unmanned aerial vehicle, UAV;automatic collision avoidance

V279+.2

A

1000-2324(2019)05-0855-06

10.3969/j.issn.1000-2324.2019.05.026

2018-03-25

2018-05-09

賈耀強(qiáng)(1997-),男,本科生,研究方向智能控制與智能系統(tǒng). E-mail:jiayaoqiangzq@foxmail.com

Author for correspondence. E-mail:xuesun@hit.edu.cn