人臉追蹤機械臂的運動學研究
崔 晨,李麗宏
(太原理工大學 電氣與動力工程學院, 太原 030600)
人機協作是工業機器人領域最熱門的研究方向之一,協作機器人已經成為一個新的研究熱點[1]。在協作機器人領域,鮮有人將人臉追蹤和機械臂結合。因此本研究設計了人臉追蹤機械臂,六軸機械臂由六個高集成度科爾摩根關節模組構成,末端連接顯示屏和Kinect視覺檢測裝置,用于將顯示屏實時跟隨人臉,協助人的日常工作,其原理如圖1所示。
人臉追蹤機械臂的工作流程如下(見圖2),首先是通過設計的上位機界面開啟Kinect視覺傳感器并使能機械臂,Kinect將實時捕捉的人臉位姿返回機械臂控制模塊。同時控制模塊通過關節模組編碼器采集電機當前位置。兩者在控制模塊中經過運動學解析得出各關節轉動量,控制機械臂運動到指定位姿。

圖1 人臉追蹤機械臂仿真原理示意圖
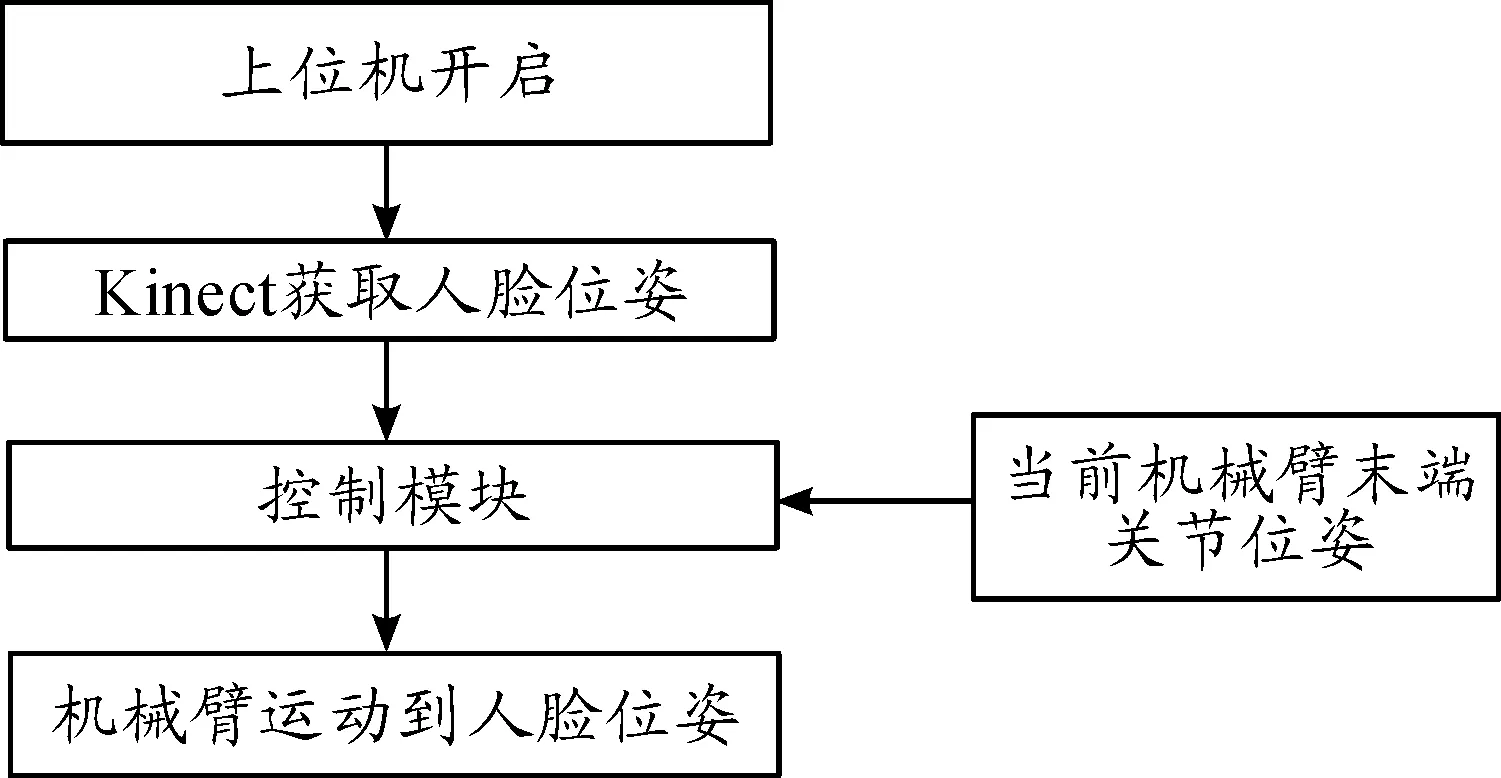
圖2 人臉追蹤機械臂工作流程框圖
而人臉追蹤機械臂的控制主要是對其末端執行器的位置和姿態進行控制,以使機械臂完成相應的動作。因此,對機械臂進行運動學分析是機械臂實現人臉追蹤必不可少的一個環節。
當前已有不少學者對六自由機械臂運動學進行了分析研究,例如:姜宏超等[2]對符合Pieper準則[3]的六自由度模塊化機械臂MT-ARM進行逆運動學分析;張化平等[4]針對MOTOMAN-MA1400安川弧焊工業機器人進行運動學分析,并運用Pro-E建立了機械臂運動仿真平臺;王立權等[5]針對6R關節型機器人推導了代數逆解結果,并研究了逆解的漏根、增根和多根問題;莫毅[6]對六自由度工業機器人建立D-H模型,通過對機器人本體的標定測量,驗證了D-H模型的正確性。
上述研究雖然都是針對六自由度的機械臂,但是機械臂機械結構均是末端三軸軸線相交于一點,符合Pieper法則之一,即3個相鄰關節交于一點;而本文后三軸軸線不相交于一點,如圖3,但是2、3、4軸軸線方向平行,如圖4,同樣滿足Pieper法則,即3個相鄰關節軸相互平行。雖然都是六自由度機械臂存在封閉解[7]的充分條件。但是因為現實中大多數機械臂符合前者相鄰三軸交于一點的條件,相應的其運動學研究也很豐富。鮮有滿足后者條件的機械臂,對應的其運動學研究較少。因此針對本機械臂,通過D-H法得到機械臂正解,而求逆解方法采用解析法[8],可以得到全部解。通過Matlab機器人工具箱檢驗正逆運動學,運用膠囊碰撞檢測算法設定約束條件選取最優解。本機械臂設定允許位置誤差范圍為10 mm,姿態角誤差范圍為0.02。
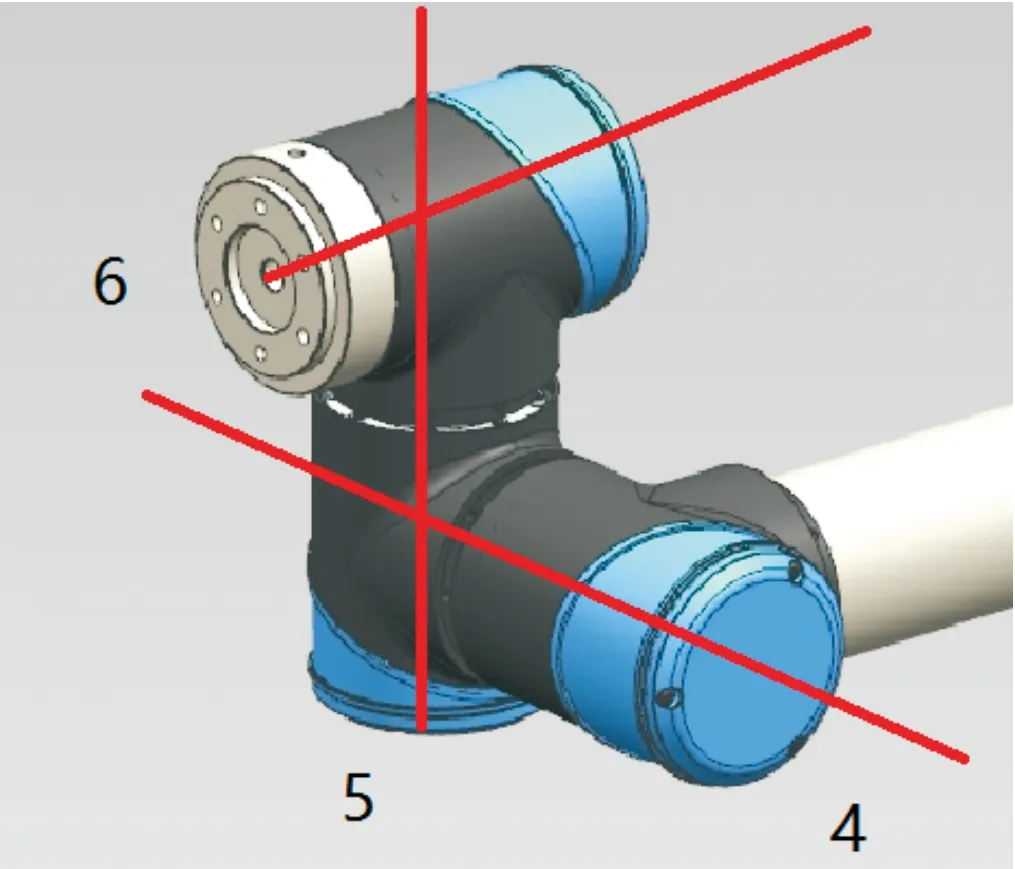
圖3 機械臂后三軸軸線示意圖
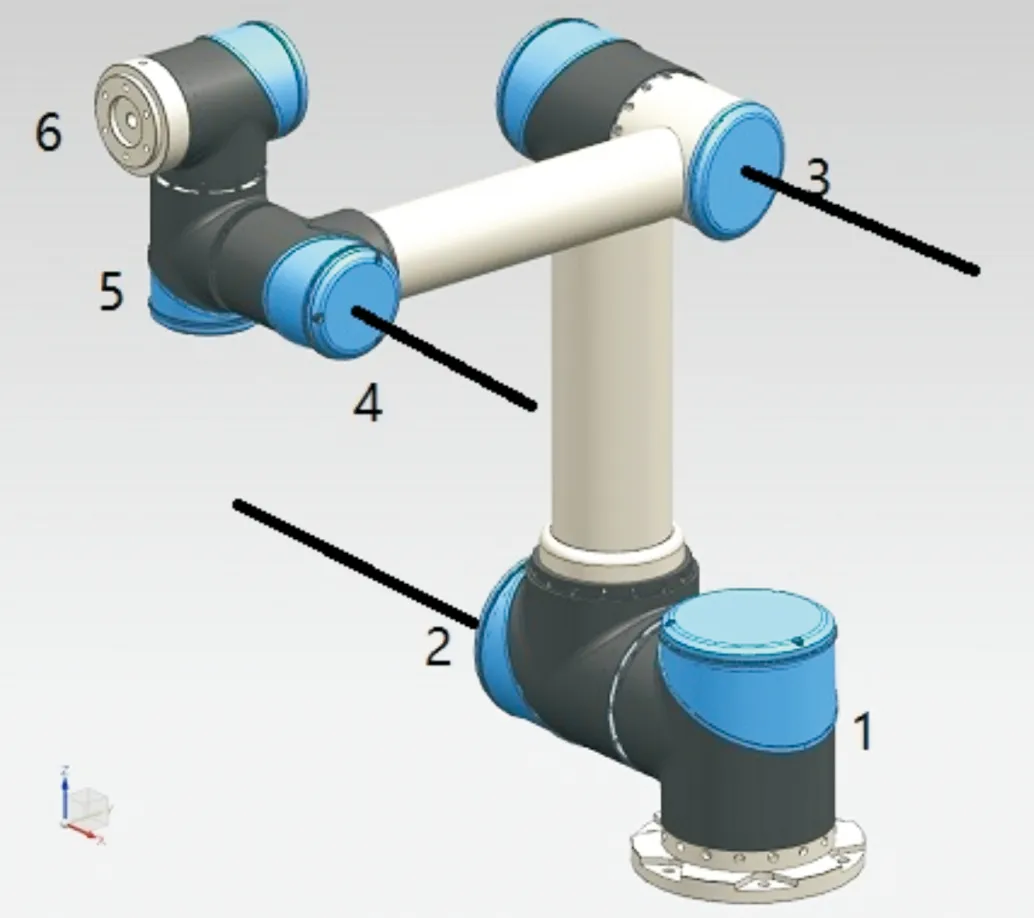
圖4 六自由度協作機械臂機械結構設計模型示意圖
1 六自由度機械臂的正運動學分析
機械臂機械結構仿照優傲公司UR系列,由六個科爾摩根RGM關節模組構成,六個關節均為轉動關節。分別為基座關節1,大臂關節2,小臂關節3,手腕關節4、5、6,分別控制俯仰角、偏航角、滾動角[9]。
采用D-H法建立連桿坐標系,分別給六個關節建立一個參考坐標系,實現任意相鄰兩個坐標系間的轉換,最后得出正運動學總變換矩陣。
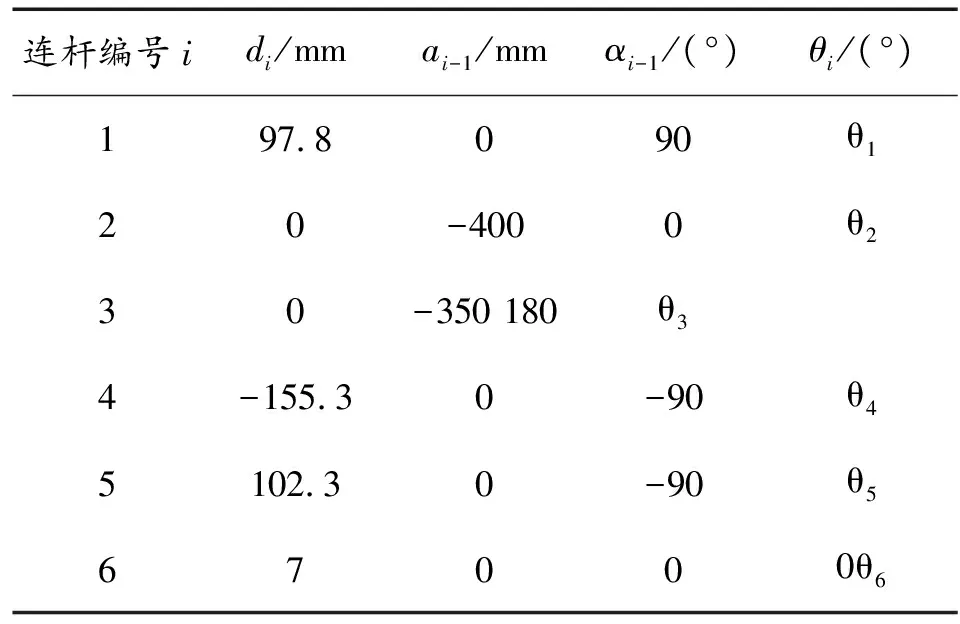
如圖5所示即為建立的六自由度協作機械臂的笛卡爾直角坐標系,表1為所建模型對應的參數值。

圖5 六自由度協作機械臂D-H坐標系
(1)
將D-H參數代入式(1),得到相鄰關節間的變換矩陣,最終得到足端坐標系相對于基座標的總變換矩陣為:
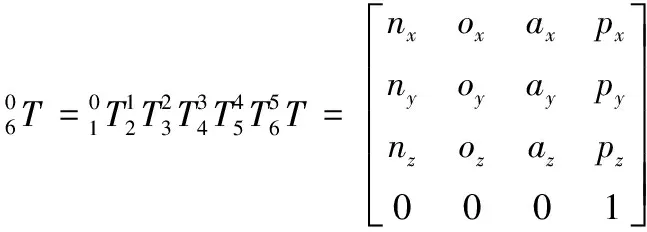
(2)
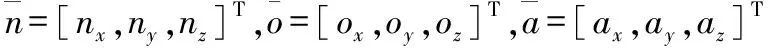
(3)
即式(3)為式(2)左上角元素構成的3維方陣。
2 六自由度機械臂的逆運動學分析
運動學逆解是已知末端位姿求解各關節角度,其解可能存在多重解,也可能無解。下面采用矩陣逆乘法[12]求解六自由度協作機械臂逆解。
2.1 首先求解θ1、θ5和θ6

(4)
由式(3)左右兩邊矩陣第三行元素相等得:
nxs1-nyc1=c6s5
(5)
oxs1-oyc1=-s5s6
(6)
axs1-ayc1=c5
(7)
pxs1-pyc1=70c5+155.3
(8)
由式(7)、式(8)得:
θ1=atan2(py-70ay,px-70ax)+
(9)
為使θ1有解,必須有(px-70ax)2+(py-70ay)2-155.32≥0,θ1有兩個解。
由等式(4)、式(5)得:
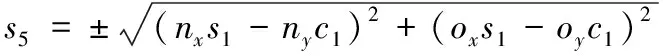
(10)
因為θ1有兩個解,所以θ5有4個解。
由式(7)、式(10)得:
(11)
當s5=0時,即θ5=nπ(n=0,1,2…),此時機構發生奇異,無法求出θ6。
當θ5≠0時,
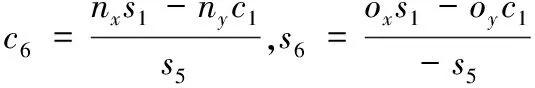
θ6=atan2(s6,c6)
(12)
將θ5代入式(12),θ6也有4個解。
式(1)等號兩端矩陣的(1,3),(2,3)元素對應相等,可得:
-c234s5=axc1+ays1
-s234s5=az
聯合求解可得:
(13)
2.2 求解θ2、θ3和θ4
(14)
令式(14)的(1,4),(2,4)元素對應相等,得:
-350c23-400c2=m1
(15)
-350s23-400s2=m2
(16)
其中,
m1=102.3s6(nxc1+nys1)-70axc1+pxc1-
70ays1+pys1+102.3c6(oxc1+oys1)
m2=pz-70az+102.3ozc6(oxc1+oys1)

(17)
θ23=atan2(400s2+m2,400c2+m1)
(18)
進而求得:
θ3=θ23-θ2
(19)
由式(13)、式(18)得:
θ4=θ234-θ23
(20)
因為m1、m2分別有4個值,所以θ2有8個解,繼而θ3和θ4也分別有8個解。
綜上所述,本研究所描述的六自由度協作機械臂最終可以得到8組逆解。
3 仿真驗證
為了驗證六自由度協作機械臂的正逆運動學的正確性,首先應用蒙特卡洛法分析了機械臂工作空間,在可達工作空間范圍內隨機選取姿態點,結合機械臂實例并利用Matlab中的機器人工具箱[13]進行驗證。下文選取一組工作空間內的位姿值闡述運動學正逆解相互驗證分析[14]的具體方法,統計出8組逆解計算精度,并進行理論分析和解釋。
3.1 六自由度機械臂工作空間分析
使用蒙特卡洛法[15]計算機械臂工作空間,基于運動學模型,通過計算機偽隨機算法,在各關節物理約束下生成關節變量,代入正解矩陣計算機械臂末端執行器的位置。
由圖6所示的三維工作空間示意圖得出,六自由度協作機械臂在X軸方向為:-882 mm到882 mm,Y軸方向:-882 mm到882 mm,Z軸方向:-363 mm到967 mm。
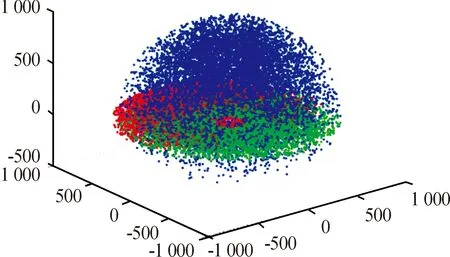
圖6 六自由度協作機械臂三維工作空間示意圖
3.2 六自由度協作機械臂正逆解驗證
選取的位姿值W=[-387.300 0、-204.600 0、487.300 0、-54°、30°、125°],位置值px、py、pz分別為:-387.300 0、-204.600 0、487.300 0和姿態角R、P、Y分別為:-54°、30°、125°。根據前文所述的逆解計算方法,運用Matlab編寫矩陣的逆解程序,將W代入編寫的Matlab逆解函數中得到8組逆解[16],如表2。
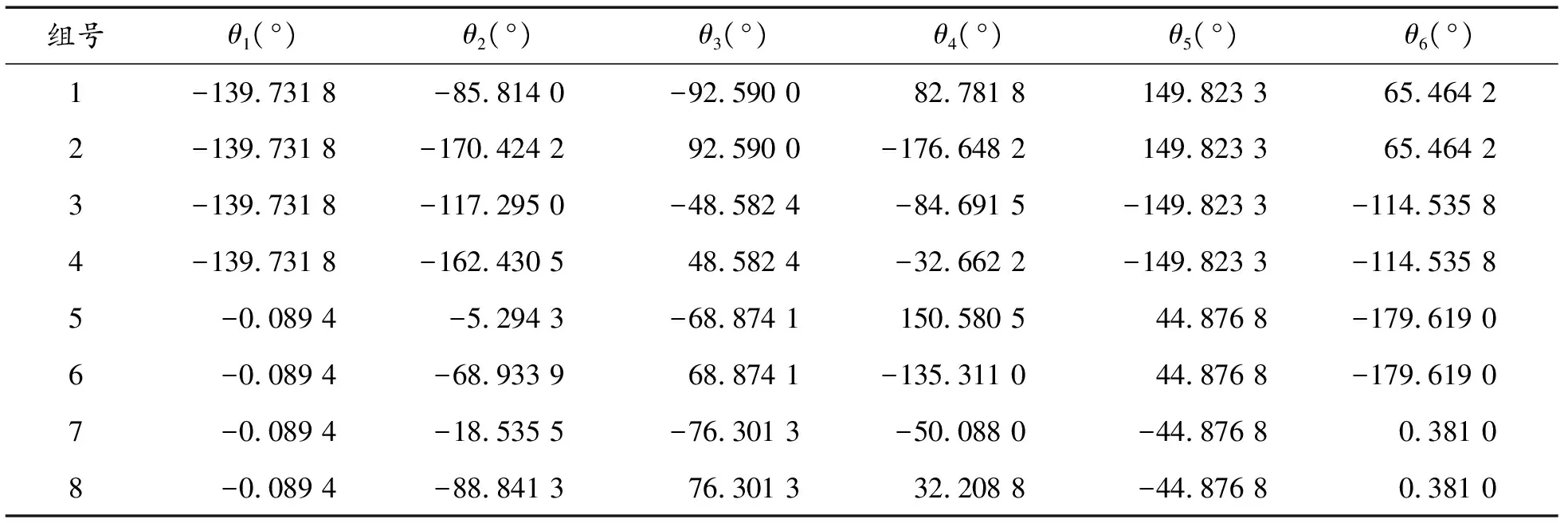
表2 8組逆解
將所得的8組逆解分別輸入機械臂控制器中,機械臂運行的最終狀態如圖7所示。

圖7 六自由度協作機械臂實際運行的最終狀態
將8組逆解依次代入正解齊次變換矩陣[17]式(2)得到8組正解矩陣。其中,T1為第一組逆解代入得到的正解矩陣。
(21)
隨后采用機器人工具箱Robotics Toolbox[17]中提供的函數對六自由度機器人建模,用表二中8組逆解中的第一組代入仿真程序得到如圖8所示的仿真結果,并得到仿真正解矩陣式(22)。
(22)

圖8 六自由度協作機械臂Matlab仿真結果
對比Matlab機器人工具箱仿真得出的正解矩陣(22)與前文正運動學建模得出的正解矩陣(21)T1。計算兩個矩陣之間的相對誤差,其余7組對比方法相同。
誤差分析分為姿態誤差和位置誤差,姿態誤差,由式(3)所示的姿態矩陣,即矩陣的左上角三維矩陣求得。位置誤差則有矩陣最后一列的位置值求得。
(23)
(24)
根據式(23)和式(24)可得全部8組誤差,如表3所示。
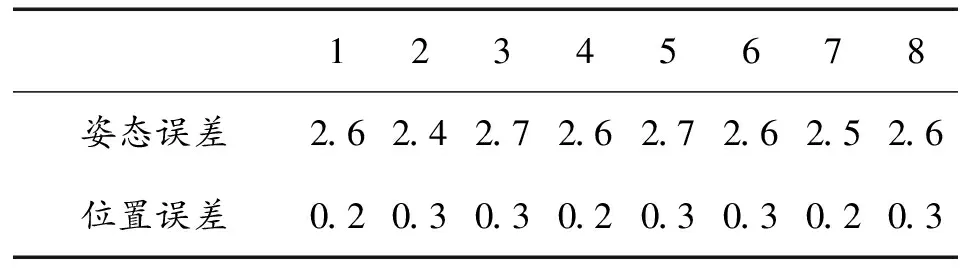
表3 誤差 ‰
由表3可得姿態誤差在2‰與3‰之間,位置誤差則保持在萬分位上,完全能夠滿足人臉追蹤機械臂得定位要求。
在機械臂可達工作空間范圍內另外選取5組位姿值,重復同樣的實驗步驟,得到的姿態誤差和位置精度與表3相符。
綜上,仿真結果均和正解矩陣得出的結果一致,證明運動學正解模型正確。
4 最優解的選取
針對六自由度協作機械臂最優解的選取經過三輪篩選,以表2的8組逆解為例進行說明。
第一輪篩選:基于機械臂物理關節約束條件,防止機械臂在運行過程中關節軸與連接桿間自身產生物理碰撞,根據機械臂機械結構得出本文六自由度協作機械臂物理關節約束如下:
-180°<θ1<180°, -180°<θ2<0
-130°<θ3<130°, -180°<θ4<180°
-160°<θ5<160°, -180°<θ6<180°
第二輪篩選:如圖7所示,機械臂安裝在工作臺上,為防止機械臂運行中觸碰工作臺,根基幾何位形,大臂和小臂的位姿形態應符合:兩者的垂直距離之和必須高于工作桌面。
因此θ2和θ3需滿足如下關系式:a3sin(-θ2-θ3)+a2sin(-θ2)<0。
經過前二輪篩選后,表2前四組解均滿足條件。
第三輪篩選:基于第二輪篩選,計算符合物理約束的每組逆解的關節轉角絕對值總和,計算結果越小,表示轉動角度和越小,轉動消耗的能量越小,第一組解計算結果最小,因此第一組解選為最優解。
5 結論
針對本研究的人臉追蹤機械臂,根據相鄰三個關節軸軸線方向平行存在封閉解這一充分條件,運用D-H法建立機械臂的關節坐標系,求得機械臂的運動學正解,采用解析法,通過矩陣逆乘求解各關節角度值。
運用蒙特卡洛法分析了機械臂工作空間,選取工作空間的位姿值,通過Matlab中的機器人工具箱,驗證了機械臂運動學正逆解的正確性,從而得到了該機械結構類型的六軸機械臂的一般性運動學逆解方法。

