電渣重熔過程電壓擺動的組合積分控制系統(tǒng)研究

李牟騰，任正云，陳安鋼，范智平，馮雪

(東華大學 信息科學與技術(shù)學院，上海 201620)

電渣重熔為特種冶金方式，屬于鋼錠的二次精煉[1]。在電渣重熔過程中，電流經(jīng)過電阻較大的電渣時會大量放熱，依靠該熱源熔化自耗電極，再通過冷凝結(jié)晶獲得質(zhì)量更高的電渣鋼。電渣重熔鋼具有純度高、含硫量低、成分均勻等優(yōu)點，廣泛應用于航天、軍工、石油、化工等領(lǐng)域[2]。因此，研究電渣重熔過程的控制系統(tǒng)對優(yōu)質(zhì)電渣鋼的生產(chǎn)有著重要意義。

電渣重熔技術(shù)的發(fā)展過程中，隨著科學技術(shù)的進步以及控制理論的發(fā)展，已有諸多學者在電渣重熔的過程控制方向取得了研究成果[3]。當前，中國的電渣爐多采用恒功率控制，而國外的電渣爐則采用更先進的恒熔速控制和渣阻控制。控制策略上，仍以常規(guī)的PID控制為主，而經(jīng)典的PID控制器對有大滯后環(huán)節(jié)的對象控制效果并不理想。雖然有些學者將模糊控制、神經(jīng)網(wǎng)絡(luò)等智能算法應用于電渣重熔的控制中，但仍存在一些缺點和不足[4]。因此，研究一種電渣重熔過程的先進控制系統(tǒng)就非常有必要，本文針對電渣重熔過程中比較先進的電壓擺動控制，設(shè)計了基于組合積分系統(tǒng)的控制器。

1 電渣重熔工藝流程

典型的電渣爐主要包括熔煉變壓器、電極夾持器、自耗電極、水冷結(jié)晶器等[5]，電渣爐結(jié)構(gòu)示意如圖1所示。熔煉過程中，通過驅(qū)動電極夾持器調(diào)整自耗電極的升降，而變壓器、電極、渣池、鋼錠等構(gòu)成了電流回路。由于渣池的電阻非常大，因此熔煉過程會大量放熱，熔化自耗電極。當金屬熔滴穿過渣池時發(fā)生的一系列物理和化學反應，去除了硫、磷等雜質(zhì)。隨著金屬熔滴的逐漸冷凝，形成了質(zhì)量高、質(zhì)地均勻的鋼錠。

圖1 電渣爐結(jié)構(gòu)示意

根據(jù)先后順序，電渣重熔過程包括起弧化渣階段、穩(wěn)定熔煉階段和熱封頂階段。起初的起弧化渣階段主要是為了使電渣充分熔化，形成穩(wěn)定熔池；最后的熱封頂階段是為了減少鋼錠的縮孔、偏析等冶金缺陷[6]。電渣重熔過程中，穩(wěn)定熔煉階段是最重要的階段，該階段熔煉過程的控制效果直接決定了最后出產(chǎn)的鋼錠質(zhì)量。因此，本文主要關(guān)注的就是電渣重熔在穩(wěn)定熔煉階段的控制。

在穩(wěn)定熔煉階段，控制熔速的穩(wěn)定是產(chǎn)出高質(zhì)量鋼錠的關(guān)鍵，渣阻大小對保持熔速的穩(wěn)定有很大影響，而自耗電極插入渣池的深度決定了渣阻的大小，因此在熔煉中需要維持電極插入渣池深度的恒定。Consarc公司在生產(chǎn)實踐中發(fā)現(xiàn)，在熔煉過程中，如果自耗電極能夠穩(wěn)定在渣池的淺層區(qū)域，則渣池的熱運動和熔融狀態(tài)的金屬液滴滴落將會導致熔渣液面產(chǎn)生微小的波動，進而引起爐口電壓有規(guī)律地波動，也就是電壓擺動[7]。由于電壓擺動的幅度可以非常靈敏地反映電極的插入深度，考慮到電極插入渣池的深度和渣阻都較難測量，因此采用壓擺控制，即控制爐口電壓在一定范圍內(nèi)擺動，即為壓擺控制的核心思路。

2 組合積分系統(tǒng)

2.1 組合積分對象的定義

組合積分對象是現(xiàn)代工業(yè)生產(chǎn)過程中的一類開環(huán)穩(wěn)定對象，常見于鋼鐵、石油化工、食品加工等[8]，式(1)給出了組合積分對象的定義：

(1)

式中：P(s)——不含積分環(huán)節(jié)的穩(wěn)定多項式。

組合積分對象的傳遞函數(shù)通常由2個或2個以上的積分時滯對象組成，在實際工業(yè)過程中，普遍存在的組合積分對象有以下五類[9]：

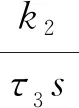
(2)

2.2 組合積分對象的本質(zhì)

假設(shè)信號f(u)的拉普拉斯變換為F(s)，當該信號經(jīng)過式(3)所示的組合積分對象X(s)：

(3)

可得傳遞函數(shù)Y(s)：

(4)

再對傳遞函數(shù)Y(s)做拉普拉斯反變換：

y(t)=L-1[Y(s)]=

(5)

從式(5)不難看出，當信號f(u)經(jīng)過組合積分對象X(s)時，相當于計算了信號f(u)在[t-τ，t]內(nèi)的均值，再乘以k，即起到均值濾波的作用。k是組合積分對象的增益，而在均值濾波過程中則可以理解為加權(quán)系數(shù)。換言之，組合積分對象本質(zhì)上是1個均值濾波器[10]。

2.3 組合積分控制器

以式(2)中的第二類組合積分對象為例，推導設(shè)計組合積分控制器。若控制系統(tǒng)具有類似圖2的單位負反饋結(jié)構(gòu)，假設(shè)系統(tǒng)的閉環(huán)傳遞函數(shù)為

(6)

那么，不難反推出控制器Gc(s)的傳遞函數(shù)為

(7)

式中：λ，τ10，τ20——控制器整定參數(shù)。

假定λ=1，τ10=τ1，τ20=τ2，則有：

(8)

進一步可以得出控制器的輸入輸出關(guān)系：

(9)

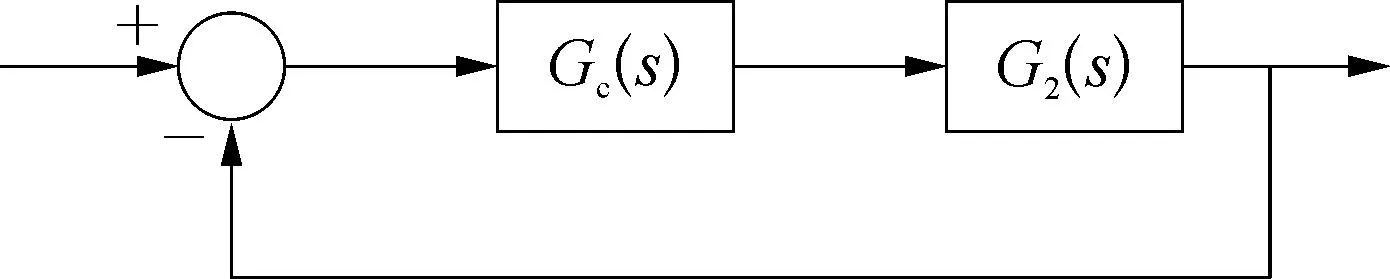
圖2 組合積分單位負反饋結(jié)構(gòu)系統(tǒng)示意

類似地，按上述過程不難推出五種組合積分對象的控制器傳遞函數(shù)，見表1所列。

表1 五種組合積分控制器傳遞函數(shù)

注： 1)M(s)=k1τ3(1-e-τ1s)+k2τ1(1-e-τ3s)e-(τ4-τ2)s。

3 電渣重熔過程建模

因為電壓擺動的大小與電極插入渣池的深度有關(guān)，所以電渣重熔過程的建模主要分為兩部分： 電極進給位置的模型和電壓擺動的模型。

3.1 電極進給位置模型

電渣爐的電極進給通常可以采用液壓驅(qū)動系統(tǒng)，而整個液壓驅(qū)動系統(tǒng)主要包括比例放大器、電液比例調(diào)速閥、液壓缸和位置反饋4個環(huán)節(jié)[11]。電極進給系統(tǒng)框圖如圖3所示。

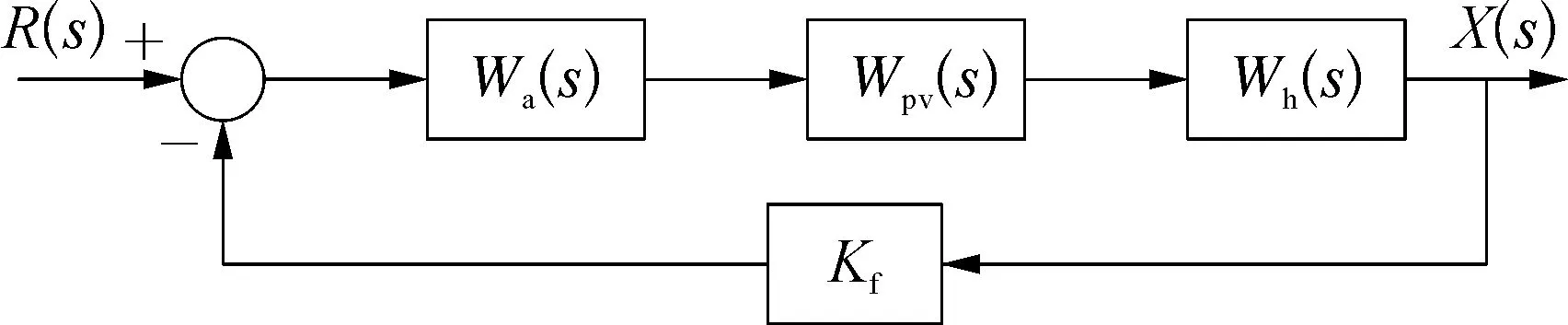
圖3 電極進給系統(tǒng)框圖示意

根據(jù)文獻[11]可以得出液壓驅(qū)動系統(tǒng)4個環(huán)節(jié)的傳遞函數(shù)，其中比例放大、位置反饋環(huán)節(jié)皆可簡化為1個比例環(huán)節(jié)，電液比例調(diào)速閥是1個二階加純滯后環(huán)節(jié)，而液壓缸則近似為1個積分環(huán)節(jié)加1個二階環(huán)節(jié)。各環(huán)節(jié)傳遞函數(shù)見表2所列。

表2 電極進給部分傳遞函數(shù)

由表2可以得出電極進給位置模型的開環(huán)傳遞函數(shù)為

Gp0(s)=Wa(s)Wpv(s)Wh(s)=

(10)

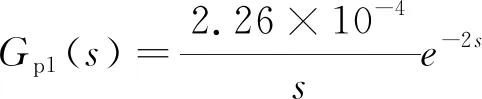
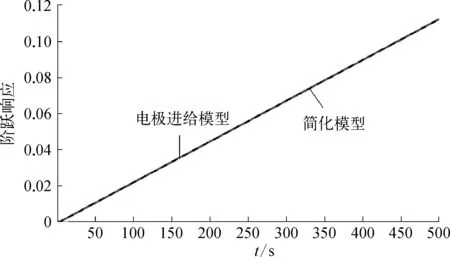
圖4 電極進給位置模型與簡化模型階躍響應對比示意

從圖4中不難看出兩者的階躍響應誤差很小，因此可將電極進給位置模型簡化為積分加純滯后環(huán)節(jié)。

3.2 電壓擺動模型

在獲得了電極進給位置模型以后，要做的就是建立從電極位置到電壓擺動的模型。由于電壓的擺動只是一個定性的描述，尚需1個量化指標描述擺動的大小。在統(tǒng)計學中，標準差可以描述數(shù)據(jù)的離散程度，因此本文在電壓擺動模型中采用爐口電壓在一段時間內(nèi)的標準差用于描述電壓的波動情況。顯然，該值越大，說明爐口電壓的波動程度越劇烈。

因此，電壓擺動模型演變?yōu)閺碾姌O進給位置到爐口電壓在一段時間內(nèi)的標準差的模型：

1)根據(jù)實際經(jīng)驗，電極進給位置與爐口電壓之間可以近似為1個比例關(guān)系，比例系數(shù)Kpv的值取10 V/m。

2)為了表現(xiàn)爐口電壓的擺動，可將爐口電壓乘以1個均值為0、方差為1的擾動信號；如果這2個信號的乘積越大，說明爐口電壓的波動越大。

信號標準差的計算，通常采用寄存器存取一段時間內(nèi)的信號值再做數(shù)學運算的方法，但該方法不利于分析被控對象的特性。因此，本文利用組合積分環(huán)節(jié)的均值濾波器的本質(zhì)，實現(xiàn)求爐口電壓標準差的過程。

信號的標準差可以使用統(tǒng)計學中的公式來計算，對于含有N個數(shù)據(jù)的信號xi={x1，x2，x3， ...，xN}，其均值μ和標準差σ可由式(11)計算得出：

(11)

對于均值的計算，可以直接用式(3)的組合積分對象來實現(xiàn)，其中k取值為1，而計算方差又可以理解為對(xi-μ)2計算均值再開根號，因此可以再串聯(lián)1個組合積分對象來實現(xiàn)。基于組合積分對象的標準差計算如圖5所示。

至此，被控對象的模型建立完畢，電壓擺動系統(tǒng)的結(jié)構(gòu)如圖6所示。

圖5 基于組合積分的標準差計算框圖示意

圖6 電壓擺動控制系統(tǒng)框圖示意

4 組合積分控制器設(shè)計

針對上述電渣重熔過程的電壓擺動模型，設(shè)計其組合積分控制器實現(xiàn)電壓擺動的先進控制系統(tǒng)。控制器是2個閉環(huán)串聯(lián)的形式，內(nèi)環(huán)控制器采用雙組合積分控制電極進給位置對象，外環(huán)的主控制器再對整個過程進行控制，從而構(gòu)成了1個串級的控制系統(tǒng)。

4.1 電極進給控制器

由于電極進給位置模型可以視作1個積分加純滯后的過程，傳遞函數(shù)為

(12)

假設(shè)期望的閉環(huán)傳遞函數(shù)為

(13)

由于被控對象的純滯后過程控制器無法調(diào)節(jié)，因此期望的閉環(huán)傳遞函數(shù)中純滯后部分的參數(shù)τ1=τ0=2，則反推控制器傳遞函數(shù)為

(14)

進一步地，控制器輸入輸出關(guān)系為

(1-e-λ1s)e-τ1sU1(s)=

(15)

根據(jù)式(15)的控制器輸入輸出關(guān)系，搭建Simulink模型，同時在第200 s時，在控制器輸出的后面加入擾動，運行并仿真控制效果，電極進給組合積分控制階躍響應如圖7所示。

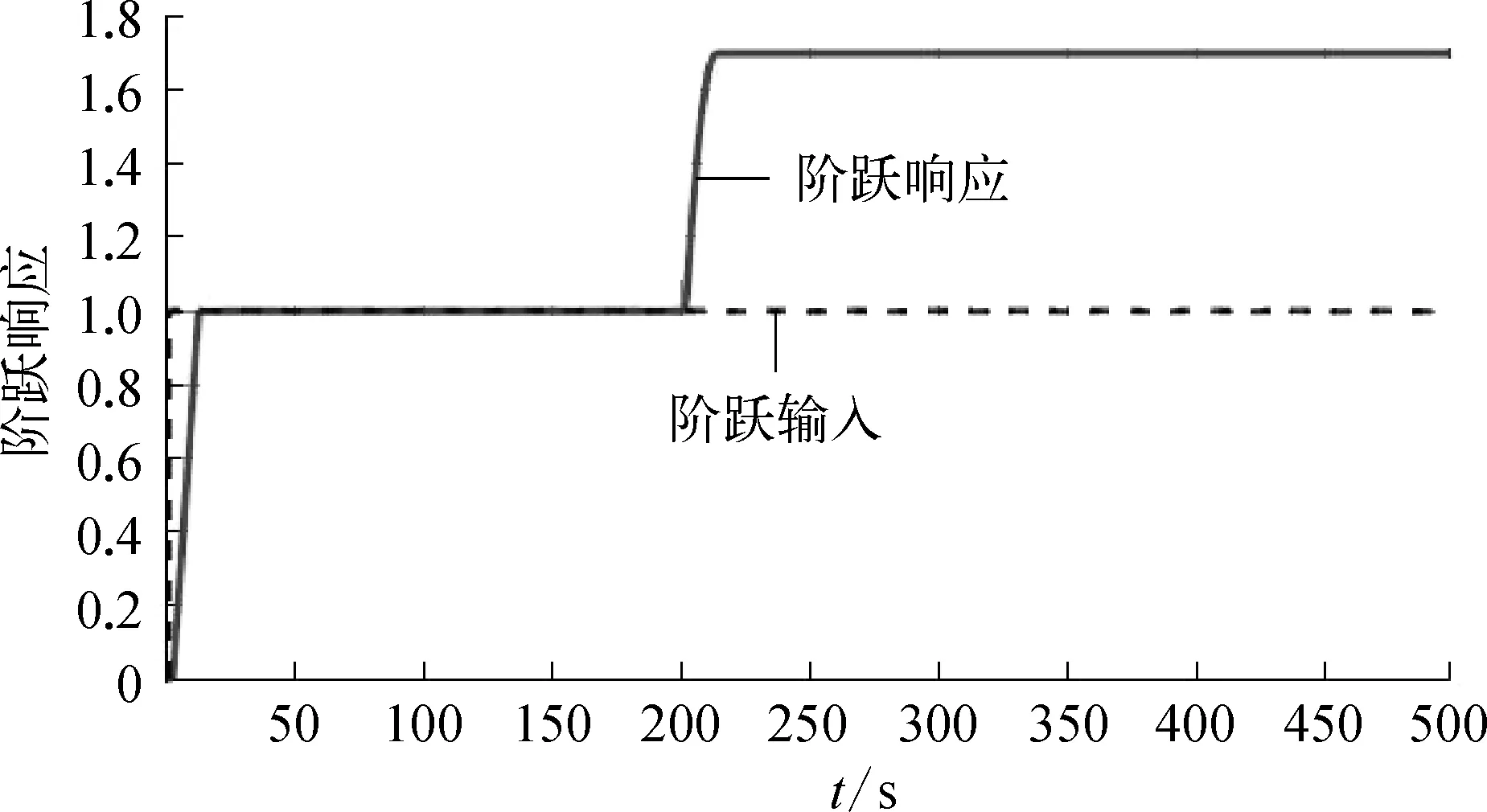
圖7 電極進給組合積分控制階躍響應示意

從圖7中可以看到，控制器跟蹤效果較好，但是當控制器輸出的后面有擾動時，存在穩(wěn)態(tài)誤差。為了解決該問題，將控制器Gc1和被控對象看作整體，再設(shè)計1個組合積分控制器，構(gòu)成雙組合積分控制器來抑制擾動。類似地，此時被控對象為

(16)

假定期望的閉環(huán)傳遞函數(shù)為

(17)

令τ2=τ1=2，反推控制器傳遞函數(shù)和控制器輸入輸出關(guān)系為

(18)

(1-e-λ2s)e-2sU2(s)

(19)

再次搭建Simulink模型，加入擾動并運行仿真后，得到圖8所示的電極進給雙組合積分控制階躍響應仿真結(jié)果。

圖8 電極進給雙組合積分控制階躍響應示意

從圖8中可以看出，通過調(diào)節(jié)參數(shù)λ1和λ2，控制器不僅控制效果好，而且可以很快地抑制擾動。

4.2 電壓擺動控制器

進給控制器設(shè)計完成后，電極進給過程的閉環(huán)傳遞函數(shù)就成為了1個組合積分過程。該過程再加上電壓擺動模型就構(gòu)成了控制系統(tǒng)外環(huán)的廣義被控對象。在設(shè)計電壓擺動的主控制器之前，先對該廣義被控對象做階躍響應測試，觀察其對象特性。調(diào)節(jié)電極進給控制器的參數(shù)，使λ1=10，λ2=20，再做階躍輸入后，得到圖9所示的電壓擺動模型階躍響應曲線。

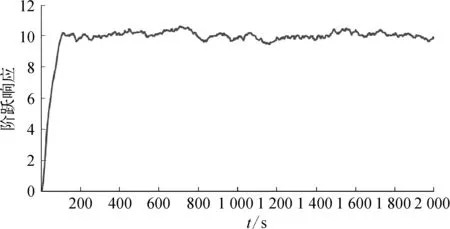
圖9 電壓擺動模型階躍響應示意

根據(jù)圖9可以看出，電壓擺動模型又可以近似為1個組合積分過程。利用最小二乘辨識法，可以得到辨識出的被控對象傳遞函數(shù)為

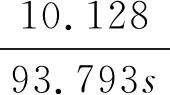
(20)

圖10對比了原被控對象與辨識對象的階躍響應曲線，可以看出階躍響應特性基本一致。

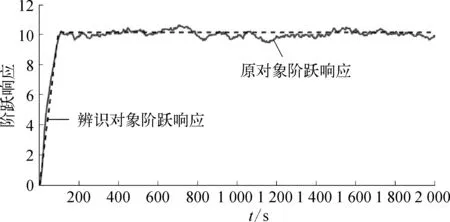
圖10 電壓擺動原模型與辨識模型階躍響應對比示意

由此，又可以根據(jù)組合積分控制器的設(shè)計思路，針對被控對象Gp3(s)設(shè)計電壓擺動的主控制器。假定期望的閉環(huán)傳遞函數(shù)為

(21)

令τ3=τ′=1.992，反推控制器傳遞函數(shù)以及控制器輸入輸出關(guān)系為

(22)

(23)

根據(jù)控制器輸入輸出關(guān)系，搭建Simulink模型。運行仿真，同時與常規(guī)PID控制方法做比較。電壓擺動組合積分與常規(guī)PID控制效果如圖11所示。

圖11是組合積分控制器和常規(guī)PID控制器的電壓標準差的響應曲線，從中可以看出組合積分控制器的響應速度要比常規(guī)PID控制器快。組合積分控制器階躍響應的調(diào)節(jié)在100 s左右，而PID控制器的調(diào)節(jié)時間則大于200 s。

圖11 電壓擺動組合積分與常規(guī)PID控制效果示意

5 結(jié)束語

本文針對帶有大慣性、大滯后特性的電渣重熔過程，基于工業(yè)過程中常見的組合積分系統(tǒng)，建立了從電極進給到電壓擺動的數(shù)學模型。針對電極進給和電壓擺動設(shè)計了串級結(jié)構(gòu)的組合積分控制器，內(nèi)環(huán)使用雙組合積分控制器控制電極進給過程，外環(huán)近似為組合積分過程后，設(shè)計了組合積分主控制器。與常規(guī)PID控制器相比較，證明了組合積分控制器具有良好的控制效果。