計算思維教育的困惑與博弈

史文崇 劉茂華 楊大志

【摘要】? ?? 在周以真的倡導下，國內外一些教育機構積極推進計算思維教育，其教學工具、測量工具得到發展，同時也暴露出各種教育活動之間差異較大、教育效果實證不足等問題。從對計算思維內涵的認識、計算思維教學內容、教學工具、教學策略、測量工具、測量結果、遷移效果等方面對國際社會計算思維教育活動現狀進行了分析，認為目前計算思維教育研究與實踐成果不足以有效支持計算思維教育，存在許多困惑和博弈;計算思維教育不能速成，反對零基礎的計算思維教育，應從知識傳遞入手，結合學習者的認知基礎，遵從思維發展規律開展教學活動;不贊成分離式教育，提倡融入式教育;建議形成研究團隊開展多項研究和實驗，形成逐層遞進的教學體系，注重教師隊伍建設，反對將計算思維教育簡單化。

【關鍵詞】? 周以真;計算思維;教學內容;教學工具;測評;遷移;皮亞杰;斯騰伯格

【中圖分類號】? G40-032? ? ? ?【文獻標識碼】? A? ? ? ?【文章編號】? 1009-458x（2019）8-00059-09

引言

周以真提出計算思維（Wing， 2006）后，一場計算思維教育改革運動在全球悄然興起。美洲、歐洲、亞洲、大洋洲的許多國家在開始傳授計算機知識之前紛紛開展K—12年級的計算思維教育;美國哈佛大學、耶魯大學、麻省理工學院、普渡大學和中國九校聯盟加盟校等高校專門開設了計算思維課程;我國在2017年推出的《普通高中信息技術課程標準（2017年版）》已將計算思維作為學科核心素養。

周以真倡導計算思維的初衷起源于計算機學科生源質量下降，有其潛在的商業目的，其更高追求則在于“讓學習者像計算機科學家一樣思考”（Wing， 2006）。但她后來又撰文，只提及國家和社會組織大量投資，生源急速上升，開設計算思維課程的教學機構增多（Wing， 2014），聲稱“取得了巨大進步”，同時也承認仍有一些“有趣的”問題值得研究（Wing， 2016），而對學習者是否能“像計算機科學家一樣思考”只字未提。那么，開展計算思維教育究竟是為了商業目的、轟動效應，還是改善學習者的思維？

關于計算思維有兩種態度：一種是絕對肯定、夸大的態度。認為計算思維“無處不在”（Bundy， 2007），是“人人必備的工具”（Barr， Harrison， & Conery， 2011），“沒有計算思維就不可能在任何學科開展研究”，倡導“將計算思維廣泛用于改善人們的生活”（CMUCCT， 2011）。另一種是質疑、反對的態度。有學者認為計算思維不適于倫理、道德、文學、美學等領域（Jones， 2011）。中國計算機教育家譚浩強認為，計算思維的發展路徑尚不明晰，主張高校計算機基礎教育應面向應用（譚浩強， 2012）;有益的思維方式很多，不應過分強調計算思維（譚浩強， 2014）。ACM前主席皮特·丹寧反對推行計算思維，擔心對計算思維的迷戀會把我們帶回曾試圖逃離的陷阱（Denning， 2009）;指責“那些狂熱者所倡導的模糊定義和未經證實的主張”“提高了無法達到的期望”，讓教師處于尷尬境地（Denning， 2017）。

在這樣的背景下，計算思維教育應何去何從？是否應該好好總結和反思？

一、計算思維定義的多樣性與理解的相對性

周以真關于計算思維的最初解釋是“利用計算學科的基礎概念求解問題、設計系統和理解人類行為”，“computational thinking，意即think computaionaly”（Wing， 2006），可將計算思維理解為一種思維風格，文中也列舉了一些特征性術語。后來她多次撰文，卻互有不同（Wing， 2008; Cuny， Snyder， & Wing， 2010; Wing， 2017），最終計算思維演變為“一個思維過程”。美國ISTE/CSTA在2011年、2013年、2015年、2016年以“計算思維的操作性定義”等形式多次給出計算思維的定義或解釋;英國皇家學會、計算機學會Computing At School分會，我國教育部高等學校大學計算機課程教學指導委員會和《普通高中信息技術課程標準（2017年版）》也都曾給出計算思維的定義或解釋，但彼此互不相同、差異極大。計算思維的倡導者和權威教育機構如此，學術界給出的計算思維的定義也一直處于發展變化之中（Selby & Woollard， 2013）。歸納起來，目前大致有思維過程說、思維風格說、學科思維說、能力要素說、知識體系說等幾類說法（史文崇， 2018; 陳鵬， 等， 2018; 范文翔， 等， 2018; 陳國良， 等， 2013; 戰德臣， 等， 2013），許多文獻已述及，這里恕不贅述。

此外，關于計算思維的定義還有另類提法。有研究者認為（Hu， 2011）計算思維是混合物，能否準確地定義計算思維并不重要;有研究者（Snow， Katz， Tew， & Feldman， 2012）認為計算思維涉及寬泛的領域，不必尋求一致定義，只要在自己的教學活動中給出清晰的定義就夠了;有研究者（史文崇， 2014）認為，理解計算思維不能靠定義，關鍵是把握其思維的計算特征與計算的思維屬性，熟練運用其典型思想。這些言論看似“另類”，但并非無稽之談，應該看到其積極、實用的一面。因為我們解析計算思維是為了開展計算思維教育，其定義不僅關系到對計算思維的理解，而且關系到其教育運作。每種定義自有其優勢或不足。即使有了全球統一的定義，因知識結構和關注焦點不同，大家對它的理解也未必相同（Aho， 2012）。學科思維、風格說有助于對計算思維的宏觀理解，但太籠統，不便開展教學，不便測量和評價;能力要素說有助于測評工具的設計和實現，但可能導致以偏概全，不能體現學科特點;過程說則既不利于理解，也不便于測評，因為處理兩種不同的事務不會有完全相同的思維過程;知識體系說則很難面向非計算機專業或中小學生實施教學。

客觀地說，計算學科具有龐大的知識體系，計算思維內涵豐富且難以窮盡，希望用一個定義、有限的要素概括其內涵，難免顧此失彼。教育者只能根據自己的理解、基于學習者的特點和教學資源，從計算學科的某些領域、特定的教學目標出發開展教學和測評。這決定了計算思維的教學和測評只能是相對的。但這種相對性如果不能概括計算學科的主旨與核心，必然偏離計算思維教育的初衷。于是，如何根據計算思維的內涵掌控計算思維教育的目標和重點就成為計算思維教育的基本困惑和博弈。

二、關于計算思維教學活動的實施

2016年周以真所謂“值得研究”的“有趣的”問題——“沒有足夠的K—12教師進行計算機科學培訓……何時教、如何教，如何衡量學習進步、學習成果和隨時間遷移的留存率”（Wing， 2016），恐怕都是教學中必須面對、又必須妥善解決的最基本的問題。美國國家研究委員會（National Research Council， NRC）關于計算思維教學的專門報告屬于總結性文件，沒有提出任何教學建議;美國CSTA在2016年年底給出的《過渡性K—12計算機科學標準》、國內的《普通高中信息技術課程標準（2017年版）》指出了蘊含計算思維的教學內容，但它們旨在規范課程教學，并非完全針對計算思維訓練，所以沒有提及用怎樣的工具、形式、測評手段開展計算思維訓練。我國教育部高等學校大學計算機課程教學指導委員會至今沒有給出其內容和目標框架體系。所以，計算思維應該教什么，應該怎么教，一直是教育者的自主行為，沒有官方依據。

（一）教學內容

教學內容是計算思維教育的載體。對計算思維內涵的理解不同，則教育者對其知識載體的選擇必有不同。目前，關于計算思維的教學內容有幾種做法：

1. 教編程

這是最普遍的做法。程序設計是計算機行業最常規的業務，此類軟件歷史最久、影響深遠，師資來源廣闊。首先想到由此入手訓練計算思維是很自然的。但編程訓練能夠改善學生的思維嗎？30多年前，皮等人（Pea， Kurland， & Hawkinsand， 1987， pp. 120-129）的研究表明，通過LOGO編程訓練不能有效改善學生的思維;有許多學者（González， González， & Fernández， 2016; Yadav， Mayfield， Zhou， Hambrusch， & Korb， 2014）將問題解決作為計算思維的核心能力之一，但賽查理斯等人（Psycharis & Kallia， 2017）最近的研究表明，編程不會明顯提高學生的問題解決能力。

程序設計雖然蘊含計算思維，但數據庫設計、網站開發、圖像處理等分支領域也同樣蘊含計算思維。如今，計算機學科有計算機科學、計算機工程、軟件工程、信息技術等多個分支，程序設計已淡出計算機學科的核心地位。以程序設計活動傳授計算思維，既缺乏全面性，又缺乏足夠的理論和實踐依據，更多的是主觀臆想。許多學者（Christopher， 2011; Lu & George， 2009; Shute， Sun， & Clarke， 2017; Grover & Pea， 2017）已認識到基于程序設計訓練計算思維的狹隘性，認為不應該在基礎計算機科學中過分強調編程技能，更不應將其作為計算思維訓練的唯一載體。

2. 教算法

自2012年起，國內一些高校以“計算思維導論”課程取代常規的計算機基礎教學，在不教授程序設計課程的情況下，試圖以算法理論為載體訓練計算思維。這實際上是將計算思維武斷地歸結為算法思維，認為普及算法知識就是培養計算思維。但算法是比程序設計更為狹小的一個子集，而且算法作為解決某一類（個）問題的工具針對性很強而普適性較差，工具論意味明顯。我們傳播計算思維旨在強化一種普遍適用的認識論。因此“計算思維就是算法思維”的觀點是一種狹隘的計算思維觀。況且，在不學習任何計算機課程的情況下直接傳授枯燥的算法知識能否被學生理解和接受？如果不能，怎能改善思維？

3. 教手工制作

有研究者（Kotsopoulos， et al.， 2017）基于建構主義和社會建構主義提出了計算思維的教學框架，包括不插電的計算機活動、手工修補、制造活動等，卻不涉及具體的計算機知識和操作;有研究者（Wojcicki， 2015）甚至提倡用玩具培養計算思維，據說適用于低齡兒童。一些機構一度曾借此培養創造性思維，如今又改頭換面用以培養計算思維，很難說沒有商業動機。這些活動遠離計算學科，充其量可以培養動手能力，至于是否包含計算思維、含有哪些計算思維則有待探討。即使蘊含某些計算思維，真的可以在低齡兒童中、在計算學科知識零基礎的情況下傳授嗎？認知心理學指出，思維的形成需經歷原塊→感塊→記塊→憶塊→思塊幾個階段，沒有感知和認知基礎，沒有知識和經驗積累，不會形成思維（Solso， MacLin， & MacLin， 2010， p. 126）。這決定了思維是不能（零基礎）直接傳授的，總是從傳授知識和間接經驗開始的。計算思維作為一種學科思維，必須從傳授計算學科知識和技能開始。而且，根據皮亞杰（Piaget， 1972， p. 186）認知發展階段理論，低齡兒童處于前運算階段晚期或具體運算階段早期，思維活動缺乏抽象性，基于遠離計算學科的手工活動，連對計算學科的具體感知都不會產生，何談理解或產生以抽象為主要特征的計算思維？

海斯（Hayes， 1985）曾把知識教學作為思維教學的一個難題，因為傳授任何一種思維方式都必須首先傳授大量的知識。可見，計算思維不能速成。急功近利不會取得好結果。前期的計算學科知識教學非常重要，必須科學選擇教學內容。

那么，計算思維應該教什么？哈佛大學、麻省理工學院、普渡大學等高校的“計算思維導論課”內容涉及程序設計、算法、網站開發、模擬等，實際上是主張全面傳播計算學科知識的。盧等人（Lu， et al.， 2009）提出應將計算思維語言（CTL）滲透到教學中。計算思維螺旋提出了一種從中學到大學有序實施的知識結構（Ioannidiou， Bennett， Repenning， Koh， & Basawapatna， 2011， pp. 82-86）。美國2014年開發了面向學生計算思維能力的“高中計算機科學原理課程框架”（Yadav， et al.， 2014）。CSP“大學預修計算機科學原理”框架大學版提出了六種計算思維實踐（College Board， 2014）。2015年，英國計算機學會計算在學校（Computing at School， CAS）分會也提出了教師指南（CAS， 2015）。孔（Kong， 2016）提出了一種指導K—12計算思維開發課程設計的七原則框架。國內學者（龔沛曾， 等， 2012）則提出，計算思維教學課程體系由大學計算機基礎課程、程序設計課程和若干門應用課程組成。各門課程應該統籌考慮、聯動改革，但內容需要充實和重組。總之，計算思維應該教什么，理論界對此見仁見智。國際上計算思維教育課程標準既不統一，又存在缺口，教學內容選擇面臨困惑和博弈。

（二）教學工具

中、英等國教育部門倡導的融入STEM或信息技術基礎課程的計算思維教育，除教材外沒有特定教學工具。目前流行的計算思維教學工具主要是一些基于編程的，在個人電腦、網絡或手機環境下使用的3D可視化編程軟件，如Scratch、Alice等，主要用于小學高年級和中學的分離式計算思維教學。這些程序設計軟件的3D可視化環境比30多年前的LOGO語言更直觀、生動，面向事件的編程環境可使學生不學習計算機語言即可利用計算機解決一些簡單問題。但他們能就此理解計算的隱喻，形成新的思維習慣或思維方式嗎？實際上，基于這種界面的訓練不過是直觀、具體的對象操作訓練。周以真（Wing， 2006）和許多學者將“抽象”作為計算思維的重要特征之一，這種直觀、具體的對象操作訓練有助于形成抽象思維嗎？答案有待考量。

國內學者也對計算思維教學工具做了探索，提出利用App Inventor程序設計平臺開展教學（梁艷瑞， 2015）、借助FunCode游戲編程平臺培養計算思維等（宋晏， 等， 2018）。但有研究者（趙姝， 等， 2012; 趙國慶， 2013）早就注意到，一些時新的教育技術并不會帶來教育教學質量或效果的本質提升。為此，加拿大教師網絡服務平臺“布魯姆板”（BloomBoard， 2014）提出計算思維工具必須結合學生的能力、學習目標和學生發展，但“這項工作還遠未完成”（Blikstein， 2015）。這無疑是計算思維教學最大的缺憾。瑞本寧等人（Repenning， Webb， & Ioannidou， 2010， pp. 102-122）指出計算思維教學工具必須滿足六個條件：低門檻、高頂棚、為心流（flow）搭起腳手架、能夠遷移、消除性別和種族歧視以及系統而可持續。其中，第一、第二、第五這三個條件最容易滿足，特別是第一個條件，低到似乎沒有門檻。為滿足第三個條件，一些教學活動在可視化、趣味性方面做了不少努力，但如果超越了學生的認知水平，仍然不會有好結果。在第四、第六個條件方面仍有較大缺口，特別是第六個條件幾乎是空白。稍加分析可知，所謂低門檻、高頂棚是指在各學段的學習中都應該有相應的教學工具。依據前述認知理論，低門檻不是沒門檻。那么，門檻應該設多高？另外，為心流搭腳手架旨在掌控學生的心理活動、激發其學習興趣和動力。那么，如何掌控和激發？如何保證實現遷移？如何保證其系統性和可持續性？這些在教學實踐中都將面臨困惑和博弈。

另外，教學工具也未必都是電子平臺或軟件。國內張錦東（2017）做了利用傳統的思維可視化工具（圓圈圖、思維導圖、雙氣泡圖）培養小學生計算思維的嘗試。斯騰伯格（Sternberg & Swerling， 1996， p.106）也提出，基于思考的提問（Thinking-based Questioning Approach）最適于思維教學。選擇科學有效的教學手段就是選擇教學工具。目前計算思維教育在這方面任重道遠。

（三）關于組織形式、教學模式

思維教學必須傳授基礎知識，但傳授知識不等于傳授思維。計算思維教育不同于傳統教學，澤爾考斯基（Czerkawski， 2013， pp. 10-17）提出計算思維課程需要更具體的教學設計策略。有些學者（李芳， 等， 2014）傾向于分離式的計算思維教學。基于上文的分析，計算思維作為學科思維必須以計算學科知識為基礎產生而不能直接傳授。即使是基于某3D可視化編程軟件的教學，無論效果如何，也是希望學生通過直觀的編程體驗獲得計算思維。所以真正的完全分離式的計算思維教學是不存在的，它只能是融入式的。從國家教育部門制定的標準看，也是倡導在課程中融入計算思維教育。哈佛大學、普渡大學的實踐是以傳播計算機學科知識為主的，實際上國內通過算法來傳播計算思維也是一種融入式的教學，只是選擇的知識載體較單薄而已。

傳統的教學方式都是面向掌握學習（mastery learning）的，但掌握學習不適于任何思維教學，因為任何人都不能說掌握了思維（Sternberg & Swerling， 1996， pp. 98-100）。因此傳統的教學和測評方式都不適于計算思維教學。國內學者梁艷瑞（2015）主張以微課程形式、唐培和等人（2018）主張以MOOC形式組織教學，牟琴等還提出了計算思維的探究教學模式（牟琴， 等， 2010）、網絡自主學習（牟琴， 等， 2011a）、任務驅動式教學模式等（牟琴， 等， 2011b）形式化的概念模型，鮑宇等（2015）提出“階梯式”引導的計算思維自主養成模式。可惜至今未見教育實驗對比結果，無法說明哪一個模式更有效或更適宜某個學段的學習者。但無論哪種教學設計，都必須基于學習者的認知基礎，符合計算思維發展規律。在計算思維教學實踐中，國內有研究者（顧堅， 2018）曾注意到“學生對老師精心設計的探究問題絲毫不感興趣，只熱衷于模仿樣例”，恰恰說明超越了學生思維能力的思維教學不會取得好的結果。有學者（趙姝， 等， 2012）提出思維訓練分隱性思維顯性化、顯性思維工具化、高效思維自動化三個階段。但這在計算思維教育中如何實踐有待研究。國外有學者（Ioannidiou， et al.， 2011）將計算思維的學習看作一種從基本的計算思維模式入手的螺旋式漸進的過程。國內有學者（牟連佳， 等， 2015）將計算思維分為信息處理、認知和元認知三個層次，并給出了層次結構模型，也有學者（史文崇， 2017）提出了計算思維的三維、四層次演進模型。這些理論有待實驗證實，但也說明學術界已注意了計算思維培養的層次性和漸進性，應該在此基礎上加大研究和探索。缺乏教育學、教育心理學理論支持，是計算思維教育研究的短板。目前尚未發現可直接推廣的計算思維教育的成功經驗。

三、關于計算思維教學的監控

——計算思維的測評

（一）評價工具

有學者（Repenning， et al.， 2010）將計算思維測量工具分為五類：總結性工具、形成性交互評價、技能-遷移工具、觀念態度量表、詞匯評估。目前，國內計算思維評價的專用工具未見文獻述及，國外計算思維工具較多。較知名的測評工具或方案有：BebrasTasks（Valentina & Futschek， 2008）、Dr. Scratch（León， Robles， & Román， 2015）、《計算思維能力水平量表》（Korkmaz， ?akir， & ?zden， 2015; Korkmaz， ?akir， & ?zden， 2017）、《計算思維模式分析（CTPA）》（Ioannidou， Bennett， Repenning， & Han， 2011）、計算思維測評軟件CTt（González， 2015; González， 2017）、三維測試框架（Brennan & Resnick， 2012）、Functional Understanding Navigator！（FUN！）（Brasiel， Close， Soojeong， Kevin， Phil， & Taylor， 2017）、計算思維實時測評系統REACT（Koh， 2017）、Ninja Code Village（NCV）（Ota， Morimoto， & Kato， 2016）、計算思維語言（computational thinking language， CTL）（Lu， et al.， 2009）、PECT（Korucu， Gencturk， & Gundogdu， 2017）、計算思維實踐評價設計模型ADPCT（Snow， Tate， Rutstein， & Bienkowski， 2017）等。其中，Bebras Tasks是基于機器人科學、面向問題解決的多任務測試;Dr. Scratch是與3D可視化程序設計軟件Scratch有關的程序設計能力測試;《計算思維量表》（CTS）是由5個大項（創造力、協作、算法思維、批判性思維、問題解決）、29個子項指標構成的五級李克特量表，是內容固定的問卷測試;《計算思維模式分析（CTPA）》是對11個計算思維模式掌握情況的測試;西班牙測試軟件CTt是基于三個維度（涉及的計算概念、答案風格、要求的任務）、由28個子項構成的測試;三維測試框架基于項目組合分析、大量訪談和手工制品考評計算思維概念和實踐;FUN！基于Scratch，由麻省理工學院媒體實驗室開發;REACT是基于心流和最近發展區理論和CPTA的實時測試;NCV建構了一種對全面學習Scratch等可視化編程語言提供支持的環境，并在此環境下開展測試，檢測程序設計常規概念、函數的使用、抽象、建模和分解方面的能力;CTL是對于計算學科常用詞匯術語記憶理解的評估測試;PECT基于CSTA關于計算思維的表述和Scratch軟件，由13個證據變量、6個設計模式變量、5個計算思維概念來打分評判，分基礎、發展、能手三個等級。ADPCT基于ECS（計算機科學探索）課程的四個單元（人機交互、問題解決、網頁設計、編程簡介），列出了以證據為中心的設計和關鍵計算思維實體五個層次（領域分析、領域建模、概念化的評估框架、評估的實施、評估交付）。上述各測評工具的特點如表1所示。

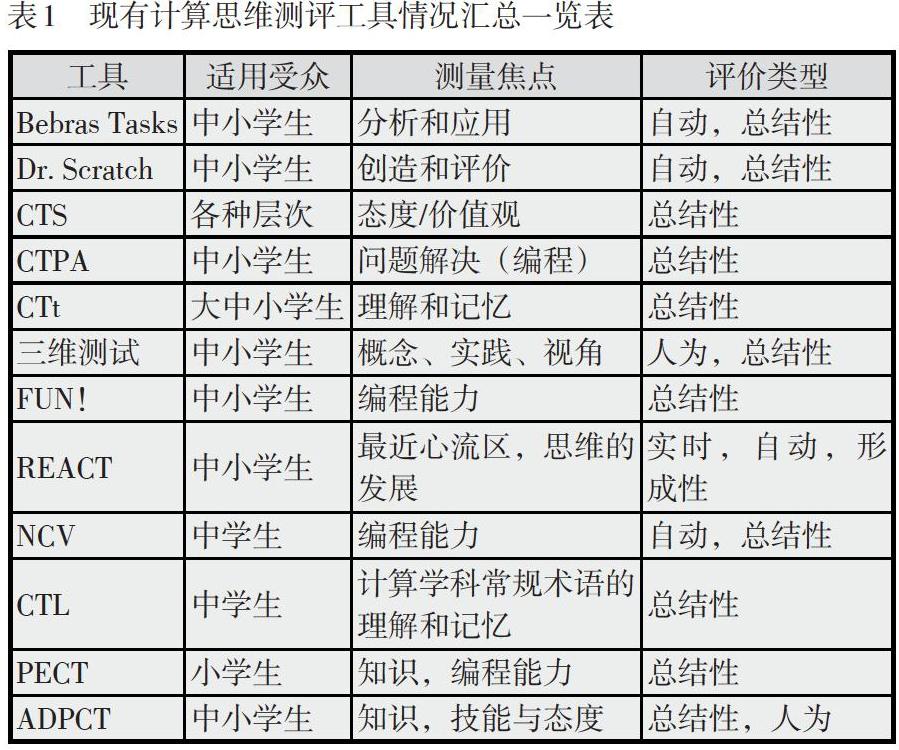
表1 現有計算思維測評工具情況匯總一覽表

[工具 適用受眾 測量焦點 評價類型 Bebras Tasks 中小學生 分析和應用 自動，總結性 Dr. Scratch 中小學生 創造和評價 自動，總結性 CTS 各種層次 態度/價值觀 總結性 CTPA 中小學生 問題解決（編程） 總結性 CTt 大中小學生 理解和記憶 總結性 三維測試 中小學生 概念、實踐、視角 人為，總結性 FUN！ 中小學生 編程能力 總結性 REACT 中小學生 最近心流區，思維的發展 實時，自動，形成性 NCV 中學生 編程能力 自動，總結性 CTL 中學生 計算學科常規術語的理解和記憶 總結性 PECT 小學生 知識，編程能力 總結性 ADPCT 中小學生 知識，技能與態度 總結性，人為 ]

由表1不難發現，在現有測評工具中，偏重低層次思維（知識、記憶）的評價工具較多，側重高層次思維（分析、評價、創造）的較少;缺乏教育心理學依據的主觀性評價多，基于教育心理學理論的客觀評價少;總結性評價工具多，形成性評價工具少;適用于中小學生的評價工具多，適用于大學生的評價工具少;側重編程能力的評價多，全面性的評價少;測試目標單一的測評工具多，綜合性的測評工具少。這種“六多六少”的局面直接影響了這些工具的科學性和實用性。其實，思維訓練測評應著眼于分析、評價、創造等高階思維能力（趙姝， 等， 2012）。有學者（唐培和， 等， 2018）不贊成用機器考試系統來檢驗學生的計算思維學習效果，主張以多種形式或途徑進行考核;郁曉華等人（2018）在分析了國際上常用的多種計算思維評價方式后認為，它們各有利弊，優劣難辨，要從中選擇完全適用且科學有效的評價工具并不容易。

（二）測評工具的完善和一致性

在測評實踐中，上述測評工具的研發者往往自己就能指出存在的問題和不足。2015年，考科莫茲等人（Korkmaz， et al.， 2015）使用《計算思維量表》（CTS）后認為，雖然中學生的計算思維能力處于較高水平，但他們解決問題的能力卻處于較低水平。這似乎是說計算思維與解決問題能力無關甚至負相關。但如果真的如此，顯然有悖于計算思維教育的初衷。那么，究竟是樣本特殊，還是測量方案存在不足？

REACT的原創者（Koh， 2017）承認，如何為焦慮和無聊區設定門檻或者為最近心流區（ZPF區域）設定閾值的問題還沒有徹底解決，這本身就是一大缺憾，勢必影響其有效性。進一步研究發現，其11種計算思維模式（CTP）源自一種游戲設計項目SGD，測評也是基于SGD項目完成的，如果離開SGD項目環境，這些CTP是否具有普適性，是否可以拓展應用于其他事務，值得商榷。如果其實用價值僅限于SGD活動，顯然與計算思維教育的本意相去甚遠。

布仁南等（Brennan， et al.， 2012）提出的計算思維三維（計算概念、計算實踐、計算視角）測試方案承認思維的形成受多種因素影響，單一的方法有其相對性，指出“沒有一種方法在理解計算思維視角的變化方面特別有效”，實際上只實現了對前兩個維度的測評。但要“讓學生像計算機專家那樣思考”，實際上就是讓他們盡可能充分地以計算（學科）視角思考。要測評計算思維教學成果，這一維度恰恰最為關鍵。關鍵維度測評方法的缺失導致該測評工具已嚴重偏離了其測試初衷。

早期（小學生）計算思維理解與評價進級模型（PECT）的研發者（Seiter & Foreman， 2013）也指出，雖然“處理技能”（process skills， 指去除bug、測試等）“在計算思維中是非常突出和重要的”，但卻“超出了研究范圍”，實際上該測評工具也缺失了原本很關鍵的測評內容。

思維的測評向來是困難的，因而一些測評項目首先測評相對容易的測評因子，這雖可以理解，但最容易評估的東西對學習者而言未必是最有價值的（Brennan， et al.， 2012）。更糟糕的是“在不同的研究中，測量結果差異很大”（Shute， Sun， & Clarke， 2017）。如，在性別差異研究中，考如庫等人（Korucu， et al.， 2017）基于CTS的測量和鐘柏昌等人（Zhong， Wang， Chen， & Li， 2016）基于三維測量框架的測量結果認為小學生的計算思維沒有顯著的性別差異，而沃呢爾等人（Werner， Denner， Campe， & Kawamoto， 2012）基于卡內基·梅隆大學計算思維中心提供的計算思維測評方案（通過算法思考，并有效地利用抽象和建模），結果認為有性別差異。亞達夫小組（Yadav， et al.， 2014）的研究結果表明，男性對計算機的興趣明顯高于女性，但又說性別不是決定計算思維的顯著因素。這說明至少有一個測評結果是錯誤的，孰是孰非？該相信誰？

可見，避重就輕、莫衷一是嚴重降低了一些計算思維測評工具的實用價值。

（三）關于知識遷移的測量

計算思維能不能遷移到其他領域？如何遷移？這關系到計算思維教育的必要性和基本路徑。海斯（Hayes， 1985）曾把知識遷移當作思維教學的一大難題;認知心理學家皮亞杰（Piaget， 1972）認為思維強化訓練不能導致思維結構的內源性變化，從根本上否認思維教育的有效性。20世紀80年代通過LOGO語言訓練兒童思維的失敗（Linn， Fisherand， & Dolbey， 1983; Pea， et al.， 1987）也為我們敲響了警鐘。客觀地說，目前關于計算思維遷移的測量研究文獻很少，知識遷移測量工具更鮮見陳述。據悉，BebrasTasks可測量向真實生活的遷移（Valentina， et al.， 2008），而CTP-Quiz可評價向科學模擬環境的遷移（Basawapatna， Koh， Repenning， Webb， & Marshall， 2011），但未見面向個人或群體的量化指標統計結果，計算學科知識遷移規律亟待探索。舒特等人（Shute， et al.， 2017）曾分析了2011——2015年的5份關于計算思維遷移的文獻中的研究成果，發現其中任一案例的遷移效果都有待進一步證實。一些計算思維典型教學案例并沒有給出有關計算知識遷移測評結果的有力證據（陳麗婷， 等， 2015），其有效性令人質疑。CTPA的研究者（Koh， 2017）聲稱“看到了遷移效果”，但分析后發現，其所謂“遷移效果”是指最近心流區（ZFP）的變化，只能說明學生能夠理解和運用某些計算思維模型了，不能說明由此形成了一種新的思維習慣或風格，更不能揭示計算思維發展規律。有些學者僅憑幾十個學生的小樣本在一段時期教學后的問卷調查結果就肯定其教學方案可行、有效（劉君亮， 2014; 葛明珠， 2014; 范帥帥， 2018），甚至就此認為學生的計算思維“正在形成”或“已經初步形成”（顧堅， 2018），未免武斷和牽強，恐怕還需更多科學的佐證材料。

總之，現有的計算思維測評工具測評焦點分散，教育心理學理論依據不足，沒有反映問題的實質，科學性和實用性亟待提高。

四、對我國開展計算思維教育的建議

綜上所述，國際社會在計算思維的內涵、教學內容、教學工具、測評工具等方面做了許多積極探索。但現有理論研究沒有得出可信的確定性的結論，實踐探索也沒有獲得成功的普遍適用的經驗，計算思維教育仍面臨許多挑戰、困惑和博弈。反對者的觀點不無警示意義。為此，本文對我國開展計算思維教育提出如下建議：

首先，要以理性、科學的態度開展計算思維教育，教學設計要有充分的理論和實踐依據，不能僅憑個人主觀愿望行事。計算思維教育是一個系統工程，不能只有計算機教師參與，應由計算學科專家、教育心理學家、思維學家形成團隊，開展多項計算思維教育實驗，就計算思維在不同學段學生中的表現形式、發展規律、測評依據、培養目標等開展研究。可以先做一些理論假設并逐一進行嘗試和驗證，但不宜大規模地普及計算思維教育。我國各地教育資源分布極不均衡，目前尤其不宜在小學及以下層次開展。

其次，切忌急功近利、將計算思維教育簡單化。思維的形成受很多因素影響，計算思維訓練是一個長期的過程，教育效果不會在短期內凸顯。不應苛求通過一門課或一項活動一蹴而就。要警惕商業性宣傳，完全指望某個教育工具軟件完成計算思維教育是不現實的，也不要過度看中某種（次）測評的結果。重在使學習者產生頓悟，實現由此及彼的認識遷移，這需要教育者更多地提供激發這種頓悟的環境或機會。教學形式、內容、測評手段應該多元化。

再次，要隨著年齡的增長，在不同階段按照學習者的思維發展規律，不斷拓展深度和廣度，明確各階段的目標，不能出現斷檔或脫節。我國教育部門劃分了高中信息技術課的計算思維等級，而大學階段卻沒有相應的等級劃分。應該努力形成從低層次向高層次逐級過渡的教學內容和評價體系。

最后，計算思維教育需要教師提高對計算思維教育的認識和工作能力。如果教師一直在誤解、困惑和博弈中煎熬，就不能搞好計算思維教育。因此，應開展各層次的教師培訓，就計算思維的內涵、價值、教學案例及其效果展開交流，明確計算思維教育旨在提升高階思維;灌輸一些事實性知識、陳述性知識不是計算思維教育;必須融入足夠的程序性知識和策略性知識，通過大量測評驗證形成科學有效的教學設計。嚴防計算思維教育陷入一些學者擔心的尷尬局面是計算思維教師的最大挑戰。

[參考文獻]

鮑宇，孟凡榮，張艷群. 2015. “階梯式”引導的計算思維自主養成模式[J]. 電化教育研究（6）：87-91.

陳國良，董榮勝. 2013. 計算思維的表述體系[J]. 中國大學教學（12）：22-26.

陳麗婷，徐曉東. 2015. 基于計算思維教育的國外小學教學案例研究[J]. 教育信息技術（9）：12-20.

陳鵬，黃榮懷，梁躍，張進寶. 2018. 如何培養計算思維[J]. 現代遠程教育研究（2）：98-112.

范帥帥. 2018. 基于Scratch培養小學生計算思維的教育實踐研究[D]. 山東：聊城大學.

范文翔，張一春，李藝. 2018. 國內外計算思維研究與發展綜述[J]. 遠程教育雜志（2）：3-17.

葛明珠. 2014. 基于計算思維的協作學習模式在中學信息技術課程中的實踐與研究[D]. 西安：陜西師范大學.

龔沛曾，楊志強. 2012. 大學計算機基礎教學中的計算思維培養[J]. 中國大學教學（5）：51-54.

顧堅. 2018. 計算思維在初中信息科技課程中的實踐研究[D]. 上海：上海師范大學.

李芳，張欣. 2014. 分離式計算思維教學探究[J]. 現代教育技術（3）：24-28.

梁艷瑞. 2015. 基于AppInventor的高職學生計算思維培養研究[D]. 成都：四川師范大學.

劉君亮. 2014. 基于計算思維的混合式學習模型研究[D]. 北京：北京交通大學.

牟連佳，李丕賢，邵洪艷. 2015. 計算思維融入信息技術教育的研究框架[J]. 科技創新導報（25）：20-23.

牟琴，譚良，吳長城. 2011. 基于計算思維的網絡自主學習模式的研究[J]. 電化教育研究（5）：51-60.

牟琴，譚良，周雄峻. 2011. 基于計算思維的任務驅動式教學模式的研究[J]. 現代教育技術（6）：44-49.

牟琴，譚良. 2010. 基于計算思維的探究教學模式研究[J]. 中國遠程教育（11）：40-45.

史文崇. 2017. 計算思維進化規律研究[J]. 河套學院論壇，14（3）： 75-82.

史文崇. 2014. 思維的計算特征與計算的思維屬性[J]. 計算機科學（2）：11-14.

史文崇. 2018. 全球計算思維研究與實踐綜述[J]. 計算機工程與應用（4）：31-36.

宋晏，姚琳，張敏，李莉. 2018. 結合FunCode游戲編程平臺的計算思維培養模式研究[J]. 計算機教育（8）：25-28.

譚浩強. 2012. 研究計算思維，堅持面向應用[J]. 計算機教育（21）： 45-49.

譚浩強. 2014. 計算機應用與科學思維能力培養——關于計算機基礎教育深化改革的思考[J]. 計算機教育（7）：4-8.

唐培和，秦福利，唐新來. 2018. 計算思維教育面臨的問題及其改革實踐[J]. 高教論壇（3）：12-14.

郁曉華，肖敏，王美玲. 2018. 計算思維培養進行時：在K-12階段的實踐方法與評價[J]. 遠程教育雜志（2）：18-28.

戰德臣，聶蘭順，徐曉飛. 2013. 計算之樹——一種表述計算思維知識體系的多維框架[J]. 工業與信息化教育（6）：9-15.

張錦東. 2017. 思維可視化工具在小學信息技術學科計算思維培養中的應用研究[J]. 教育觀察（8）：50-52.

趙國慶. 2013. 經典思維教學程序的分類、比較與整合[J]. 開放教育研究（6）：62-72.

趙姝，趙國慶，吳亞濱. 2012. 思維訓練：技術有效促進學習的催化劑[J]. 現代遠程教育研究（4）：28-34.

Aho， A. V. （2012）. Computation and computational thinking. Computer Journal， 55（7）：832-835.

Barr， D.， Harrison， J.， & Conery L. （2011）. Computational thinking： A digital age skill for everyone. Learning & Leading with Technology，38（6）：20-23.

Basawapatna， A.， Koh， K. H.， Repenning， A.， Webb， D. C. & Marshall， K. S. （2011）. Recognizing computational thinking patterns. Paper presented at the the 42nd ACM technical symposium on computer science education （SIGCSE）， Dallas， TX， USA.

Blikstein， P. （2015）. Computationally enhanced toolkits for children： Historical review and a framework for future design. Foundations and Trends in Human-Computer Interaction， 9（1），1-68.

Bloomboard. （2014， Febrary 16）. Selecting appropriate tools for computational thinking. Retrieved from https：//microcredentials-static.s3.am azonaws.com/402/SelectingAppropriateToolsforCT.pdf

Brasiel， S.， Close， K.， Soojeong J.， Kevin L.， Phil， J.， & Taylor， M. （2017）. Measuring computational thinking development with the FUN！ tool. Emerging Research， Practice and Policy on Education， （4）：36-48.

Brennan， K.， & Resnick M. （2012）. New frameworks for studying and assessing the development of computational thinking. Mark. J. eds. Procedings of AERA 2012. Vancouver， BC， Canada.

Bundy， A. （2007）. Computational thinking is pervasive. Journal of Scientific and Practical Computing， （1）：67-69.

Carnegie Mellon University Center for Computational Thinking. （2011， October 20）. Computational Thinking For Everyone. Retrieved from http：//www.cs.cmu.edu/CompThink/CTforeve.html

Christopher， H. C. （2011）. Assessing the impact of computer programming in understanding limits and derivatives in a secondary mathematics classroom. Middle-Secondary Education and Instructional Technology， （12）：70-79.

College Board. （2014， March 18）. AP computer science principles draft curriculum framework. Retrieved from https：//advancesinap.collegeboard.org/stem/computerscienceprinciples/AP computer science principles.html

Computing at School. （2015， June 8）. Computational thinking： A guide for teachers. Retrieved from https：//community.computingatschool.org.uk/resources/2324/Computa-tional_Thinking_A_Guide_for_Teachers.html

Cuny， J.， Snyder L.， & Wing J. M. （2010， Feburary 18）. Demystifying CT for noncomputer scientists. Retrieved from http：//www.cs.cmu.edu/comp think/resources/wing.pdf

Czerkawski， B. （2013）. Instructional design for computational thinking. In R. McBride & M. Searson （Eds.）， Proceedings of Society for Information Technology & Teacher Education International Conference 2013（pp. 10-17）. Chesapeake， VA：AACE.

Denning， P. J. （2009）. The profession of it beyond computational thinking. Communications of the ACM，52（6）：28-30.

Denning， P. J. （2017）. Remaining trouble spots with computational thinking， Communications of the ACM，60（6）：33-39.

González， M. R. （2015）. Computational thinking test： Design guidelines and content validation //Proceedings of EDULEARN15 conference， 2015：4203-4329.

González， M. R. （2017）. Complementary tools for computational thinking assessment. In macard， H. Ed. Proceedings of International Conference on Computational Thinking Education，（7）：228-242.

González， M. R.， González， J. C. P.， Fernández， C. J. （2016）. Which cognitive abilities underlie computational thinking？ Criterion validity of the Computational Thinking Test. Computers in Human Behavior，10（8）：47-59.

Grover， S.， Pea， R. D. （2017， December 10）. Computational thinking： A competency whose time has come. Retrieved from https：//www.researchgate.net/322.html

Hayes， J. R. （1985）. Three problems in teaching general skills. In S. F. Chipman， J. W. Segal， & R. Glaser （Eds.）， Thinking and learning skills： Research and open questions， 2， 391-406. Hillsdale， NJ： Erlbaum.

Hu， C. （2011）. Computational thinking： What it might mean and what we might do about it. Proceedings of the 16th annual joint conference on innovation and technology in computer science education. Darmstadt， Germany： ACM.

Ioannidou， A.， Bennett， V.， Repenning A.， Han K. K.， & Basawapatna， A. （2011）. Computational thinking patterns. Division C of proceedings of AERA 2011， Colorado America.

Jones， E. （2011， October 28）. The trouble with computational thinking. Retrieved from http：//www.creader.com/news/trouble.html

Koh， K. H. （2017， June 12）. Real time assessment of computational thinking. Retrieved from http：//www.academia.edu

Kong， S. C. （2016）. A framework of curriculum design for computational thinking development in K-12 education. Journal of Computers in Education，3（4），377-394.

Korkmaz， ?.， ?akir， R. M.， & ?zden， Y. （2015）. Computational Thinking Levels Scale （Ctls） adaptation for secondary school level. Gazi Journal of Education Sciences，1（2）：143-162.

Korkmaz， ?.， ?akir， R. M.， & ?zden， Y. （2017）. A validity and reliability study of the computational thinking scales. Computers in Human Behavior. Volume 72 Issue C，（7）：558-569.

Korucu， A. T.， Gencturk， A. T.， & Gundogdu， M. M. （2017）. Examination of the computational thinking skills of students， Journal of Learning and Teaching in Digital Age，2（1），11-19.

Kotsopoulos， D.， Floyd， L.， Khan， S.， Namukasa， I. K.， Somanath， S.， Weber， J. & Yiu， C. （2017）. A pedagogical framework for computational thinking. Digital Experiences in Mathematics Education，3（2），154-171.

León， M.， J.， Robles， G.， & Román， M. （2015）. Dr. Scratch： Automatic analysis of scratch projects to assess and foster computational Thinking. Revista de Educación a Distancia，（6）：30-46.

Linn， M. C.， Fisherand， C. W.， & Dolbey， J. The effects of learning to program and learning from cognitively demanding software [R]. Berkeley， C. A. ： University of California，1983.

Lu， J. J.， & George， H. L. （2009）. Thinking about computational thinking. SIGCSE09， March 3-7， 2009， Chattanooga， Tennessee， USA.

Ota， G.， Morimoto， Y.， & Kato， H. （2016）. Ninja code village for scratch： Function samples/function analyser and automatic assessment of computational thinking concepts. In VL/HCC， 2016 IEEE Symposium on （pp. 238-239）.

Pea， R. D.， Kurland， D. M.， & Hawkinsand， J. （1987）. LOGO and the development of thinking skills. Norwood N. J.， USA：Ablex Publishing Corp.

Piaget， J. （1972）. Psychology and epistemology： Towards a theory of knowledge. London： Oxford University Press.

Psycharis， S.， & Kallia， M. （2017）. The effects of computer programming on high school students reasoning skills and mathematical self-efficacy and problem solving. Instructional Science， 45（7）：583-602.

Repenning， A.， Webb， D.， & Ioannidou， A. （2010）. Scalable game design and the development of a checklist for getting computational thinking into public schools. Papers presented at the To appear in the proceedings of the 2010 ACM SIGCSE conference， Milwaukee， WI.

Seiter， L.， & Foreman， B. （2013）. Modeling the learning progressions of computational thinking of primary grade students. Proceedings of the ninth annual international ACM conference on international computing education research， Pages 59-66 ， San Diego， San California， USA.

Selby， C.， & Woollard， J. （2013， October 18）. Computational thinking： The developing definition. University of Southampton. Retrieved from https：//eprints.soton.ac.uk/356481/ddus.html

Shute， V. J.， Sun， C.， & Clarke， J. A. （2017）. Demystifying computational thinking. Educational Research Review，（9）：1-17.

Snow， E.， Katz， I.， Tew， A. E.， & Feldman， J. （2012）. Assessing computational thinking. NSF-CE21 community meeting， Washington， D. C. February 2-3， 2012.

Snow， E.， Tate C.， Rutstein D.， & Bienkowski， M. （2017， October 12）. Assessment design patterns for computational thinking practices in exploring computer science. Menlo Park， CA： SRI International. Retrieved from http：//pact.sri.com/resources.html

Solso， R. L.， MacLin， M. K.， & MacLin， O. H.. （2010）. Cognitive psychology. Washingtown： Wadsworth Publishing.

Sternberg， R. J.， & Swerling L. S. （1996）. Teaching for thinking： Becoming smart learner. Newyork： American Psychological Association.

Valentina， D.， & Futschek， G. （2008）. Bebras international contest on informatics and computer literacy： Criteria for good tasks. Informatics Education Supporting Computational Thinking， （7）：19-30.

Werner， L.， Denner， J.， Campe， S.， & Kawamoto， D. C. （2012）. The fairy performance assessment： Measuring computational thinking in middle school. In Proceedings of the 43rd ACM technical symposium on computer science education. ACM， pp. 215-220.

Wing， J. M. （2006）. Computational thinking. Communications of the ACM， 28（9）：23-28.

Wing， J. M. （2008）. Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society， 10（4）：3717-3725.

Wing， J. M. （2014， January 10）. Computational thinking benefits society. Retrieved from http：//socialissues.cs.toronto.edu/D29.html

Wing， J. M. （2016， March 24）. Computational thinking， 10 years later. Retrieved from https：//www.Microsoft.Com/Res/CT.html

Wing， J. M. （2017）. Computational thinkings influence on research and education for all. Italian Journal of Educational Technology， 25（2），7-14.

Wojcicki， E. （2015， January 2）. Dash and dot： The best toy to teach computational thinking. Retrieved from https：//www.huffingtonpost.com/esther-wojcicki/dash-and-dot.html

Yadav， A.， Mayfield， C.， Zhou， N.， Hambrusch， S.， & Korb， J. T. （2014）. Computational thinking in elementary and secondary teacher education. ACM Transactions on Computing Education， 14（1）：1-16.

Zhong， B.， Wang， Q.， Chen， J.， & Li， Y. （2012）. An exploration of three-dimensional integrated assessment for computational thinking. Educational Research Review， （10）：18-27.

收稿日期：2018-08-18

定稿日期：2019-01-10

作者簡介：史文崇，碩士，副教授;劉茂華，博士研究生，講師;楊大志，博士研究生，講師。河北科技師范學院數學與信息科技學院（066004）。

責任編輯 單 玲