回歸與矩陣分解的業務過程時間預測算法

李帥標,趙海燕,陳慶奎,曹 健

1(上海理工大學 光電信息與計算機工程學院 上海市現代光學系統重點實驗室 光學儀器與系統教育部工程研究中心,上海 200093) 2(上海交通大學 計算機科學與技術系,上海 200030)E-mail:2609215537@qq.com

1 引 言

為了在這個競爭激烈的社會環境中生存,企業必須實現高效的工作流程.時間作為業務流程中的重要因素,在近幾年得到了越來越多的關注,企業對時間方面的要求也越來越苛刻[1].幸運的是,在信息技術快速發展的前提下,越來越多的企業正在使用業務流程信息系統(Process-Aware Information Systems,PAISs)來支持他們的業務[2].系統將業務流程執行的蹤跡和已執行活動的信息或屬性記錄在稱為事件日志的文件中,使企業積累大量數據信息.近些年來,很多學者開始研究如何對業務過程的執行時間進行預測的問題.

對具有復雜性和靈活性的業務過程來說,準確的時間預測并不容易,因為其執行方案和性能隨時間會發生變化,所以準確的預測結果取決于當前活動上下文環境[3].上下文環境對預測的結果和精確度有很大的影響,如時間、位置以及場景等信息.例如,對于快遞業務而言,即使運送的路線相同,也會因為不同的季節導致的交通狀況不同從而使得時間具有很大差別.因此考慮上下文環境對業務過程進行時間預測是極其重要的.

近年來,矩陣分解算法(Matrix Factorization,MF)的應用越來越廣泛,傳統矩陣分解技術主要包括奇異值分解(Singular Value Decomposition,SVD)[4]、非負矩陣分解(Non-negative Matrix Factorization,NMF)[5]和概率矩陣分解(Probabilistic Matrix Factorization,PMF)[6]等.上述模型的共同特性是將高維矩陣轉換為多個低維矩陣乘積來達到降維的目的,其中以概率矩陣分解應用最為廣泛[7].基于矩陣分解的算法是假設最終結果受到多個隱特征的影響,通過隱特征空間將用戶與物品聯系起來.又因存在的隱特征無法準確的歸納為某些具體特征,故矩陣分解模型也被稱為隱語義模型.因此,在假設結果受到隱特征或不可列舉因子影響的前提下,我們結合矩陣分解思想提出一種基于回歸與聯合概率矩陣分解(Regression and Collective Probabilistic Matrix Factorization,RCPMF)的算法用于業務過程時間的預測.在該算法中,對于可觀測的特征部分,我們使用回歸模型進行學習;對于不可觀測的特征部分(隱因子或潛在特征),我們使用聯合概率矩陣分解模型進行學習;最后將兩部分的結果相結合作為最終的預測結果.

2 相關工作

目前很多學者在對業務過程時間方面進行預測時都考慮了上下文環境因素,其實驗結果表明考慮上下文信息對預測效果有積極影響[12].

文獻[8]中,Polato等人使用了一種ε-SVR機器學習算法對業務過程進行剩余執行時間的預測.該方法使用業務過程的歷史蹤跡活動屬性信息訓練ε-SVR模型,并通過編碼技術將部分蹤跡的特征轉換為適合模型輸入的格式,輸出的值即為估計的剩余執行時間.文獻[9,10]中,Folino等人根據上下文特征對日志蹤跡進行聚類,然后,對于每個聚類創建剩余活動時間預測模型.為了對新的業務過程進行預測,首先根據其特征將其聚類,然后使用屬于特定集群的模型進行預測.在文獻[11]中,作者利用事件日志的上下文信息生成決策樹用來發現業務流程特征之間相關性.并在此基礎上想對業務過程剩余時間進行預測.由于決策樹需要將數值離散化,降低了方法準確性,故作者沒有提供相關的預測示例.在文獻[12]中,Polato等人考慮事件的附加屬性以改進時間預測質量.該方法利用了在標記變遷系統(An Annotated Transition System)添加樸素貝葉斯分類器和支持向量回歸器的想法,實驗結果表明考慮附加屬性能夠對預測結果產生積極影響.另外,Leitner 等人[13]根據記錄的歷史數據,使用WEKA 機器學習框架來構建回歸模型.對于正在運行的業務過程,將可用的特征信息輸入預測回歸模型,輸出服務水平協議(Service Level Agreement,SLA)值,即時間預測值.通過與規定的SLA值比較判斷該業務過程是否會超時.

以上是對業務過程活動時間方面的相關預測方法的介紹,上述方法雖然考慮活動的附加屬性,但沒有考慮業務過程受到了許多因素的影響,雖然有些因素是明確的,但是還有許多難以明確建模的隱因素對業務過程時間具有很大的影響.針對這一特點,我們將回歸模型與聯合概率矩陣分解模型應用于業務過程活動的時間預測.實驗結果表明,該算法考慮了更多的上下文環境特征,具有更高的預測精度.

3 基于回歸與聯合概率矩陣分解的業務過程時間預測算法

3.1 算法思想介紹

本文所提出的算法是為了解決在不同上下文環境下可觀測特征與不可觀測特征對結果有所影響的問題.該算法不只是局限于某種特定的上下文環境,其上下文環境可根據具體的業務過程背景有所不同,例如時間上下文或位置上下文等,故該算法在一定程度上滿足靈活性與通用性.

該算法假設結果受到可觀測特征與不可觀測特征的影響,在確定上下文環境類型后,對于可觀測特征部分,使用回歸模型進行學習,對于不可觀測特征部分,使用聯合概率矩陣分解進行學習.

3.2 問題的定義

為了方便進行形式化描述,本文所使用的符號標記如表1所示.

表1 符號表Table 1 Notations

表1中US表示不同隱特征矩陣所對應的用戶數目集合,E表示不同用戶隱特征矩陣與物品隱特征矩陣的時間偏差矩陣集合.

3.3 概率矩陣分解模型

目前,以概率方式預測用戶對物品的喜愛程度的矩陣分解模型被大部分的研究人員使用.在本文中,我們使用概率矩陣分解的思想預測業務活動的時間偏差.在假設用戶隱特征向量、物品隱特征向量以及活動時間偏差服從高斯分布的前提下,首先利用貝葉斯公式推導用戶隱特征向量與物品隱特征向量的后驗概率,然后利用隨機梯度下降法(Stochastic Gradient Descent,SGD)進行求導[14].

已知時間偏差數據的條件概率分布函數如公式(1)所示.式中U表示n=1時,U的用戶隱特征矩陣集合,即U=U1;E表示n=1時,E的時間偏差矩陣集合,即E=E1:

(1)

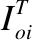
(2)

(3)

根據貝葉斯推理,隱特征向量U和V的后驗概率分布函數:

(4)

根據公式(4),通過用戶物品時間偏差矩陣,我們能夠學習用戶和物品的隱特征向量,相應的概率模型圖如圖1所示.

3.4 RCPMF模型框架

本文提出一種回歸與聯合概率矩陣分解的業務過程時間預測算法,該算法主要有以下幾個部分組成:

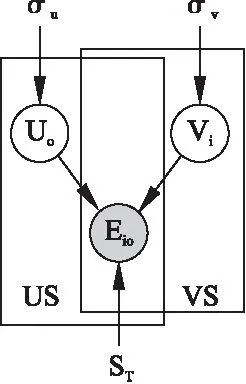
圖1 概率矩陣分解圖模型Fig.1 Graph model for probabilistic matrix factorization

1)獲取可觀測特征.根據已有的事件日志文件,通過數據預處理、特征篩選、特征提取等步驟獲取對時間有影響的活動特征.

2)求取時間偏差.根據可觀測特征,使用普通最小二乘法求取最優的回歸系數,通過回歸模型預測活動執行時間,最后將預測時間與活動真實執行時間之差作為回歸模型預測所產生的時間偏差.

3)學習隱特征矩陣.在假設時間偏差受到不同隱特征矩陣影響的前提下,將時間偏差矩陣集合E中不同的偏差矩陣融入到概率矩陣分解中,將最大化聯合后驗概率設定為目標函數,通過隨機梯度下降算法學習最優的用戶隱特征矩陣集合與物品隱特征矩陣集合.

4)預測時間偏差.根據不同部分的用戶隱特征矩陣和物品隱特征矩陣計算得到在其對應部分所預測的時間偏差.

5)業務活動持續時間預測結果.將回歸模型預測時間與聯合概率矩陣分解預測不同部分的時間偏差相結合作為最終的時間預測結果.

3.4.1 回歸模型

本文所使用的回歸模型為線性回歸模型,我們假設在回歸模型中所使用的上下文特征已經消除特征多重共線性,線性回歸表示每個特征對整體預測結果所做的貢獻,通過加權求和的方式預測最終結果.假定輸人特征數據存放在矩陣Χ中,而回歸系數存放在向量w中,通過利用平方誤差求出向量w使得預測時間值和真實時間y值之間的差值最小.平方誤差公式如下:

(5)

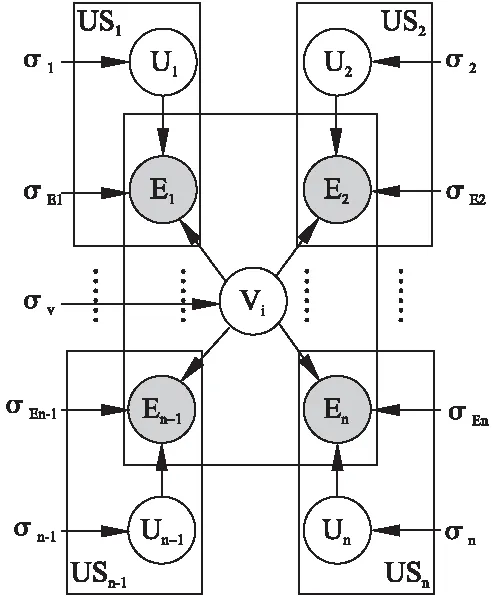
圖2 聯合概率矩陣分解圖模型Fig.2 Graph model of collective probabilistic matrix factorization

通過對(5)式使用普通最小二乘法(ordinary least squares)即可求出最優系數向量.

3.4.2 聯合概率矩陣分解模型

在不確定上下文環境時,我們不知道其結果受到多少種因素或場景的影響,因此將影響因素數目或場景數目設置為n,場景集合S={S1,S2,…,Sn},故所提出的聯合概率矩陣分解部分的圖模型如圖2所示.

根據模型得用戶數目集合US={US1,US2…USn},用戶隱特征矩陣集合U={U1,U2,…,Un},時間偏差矩陣集合E={E1,E2,…,En}.為了便于理解推導過程,在此處將影響結果的場景數目設置為2進行推導,即S={S1,S2}.

聯合概率矩陣分解圖模型基于以下假設:

1)假設物品隱特征矩陣Vi,場景S1中用戶隱特征矩陣U1的先驗概率服從高斯分布且相互獨立,則滿足下列公式.

(6)

(7)

其中N(x|μ,σ2)表示均值為μ,方差為σ2的高斯分布概率密度函數,I為單位矩陣.同理可得場景S2中用戶隱特征矩陣U2滿足公式(8).

成分不同，安全劑量不同。對乙酰氨基酚的日常最大用量為每4小時1次，每次15mg/kg，如孩子體重超過44千克，可參考成人劑量1000mg/次或4000mg/日。布洛芬的日常最大用量為每6小時1次，每次10mg/kg，如孩子體重超過44千克，可參考成人劑量600mg/次或2400mg/日。

(8)

(9)

(10)

用戶與物品之間存在的時間偏差受不同場景的影響,所以聯合概率矩陣分解部分將不同場景中用戶與物品的關系矩陣的分解結合起來.由圖2可以推出U1,U2,V的后驗概率分布函數.后驗分布函數的對數函數滿足公式(11):

(11)

其中,C是一個獨立于參數的常量.最大化方程(11)等價于最小化方程(12):

(12)

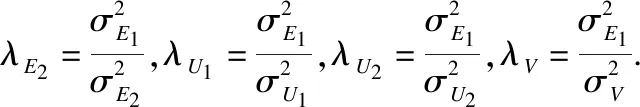
根據隨機梯度下降法,如下所示:

(13)

(14)

(15)

公式(13)-公式(15)在算法中用于更新各個隱特征向量值.

4 實驗和結果分析

4.1 實驗數據

為了驗證模型,本文使用兩種不同業務過程的數據集.第一個實驗數據集來自國內某服裝企業2015年1月-2018年4月在面料采購環節所記錄的真實數據,該數據集反應了不同面料供應商在生產不同類型的面料時所花費時間的真實情況.原始數據集包括133個供應商,7337種面料類型,11219條供應商生產面料所需時間的記錄.第二個實驗數據集來自福特GoBike自行車2017年6月-2018年6月所記錄騎行時間的真實數據,該數據集反應不同年齡的用戶在行駛不同路徑所需時間的真實情況.原始數據集包括53種用戶年齡等級,10895條行駛路徑,35658條不同年齡等級用戶騎行不同路徑所需時間的記錄.

4.2 場景分析

對數據集1與數據集2中過程持續時間分析如圖3所示.

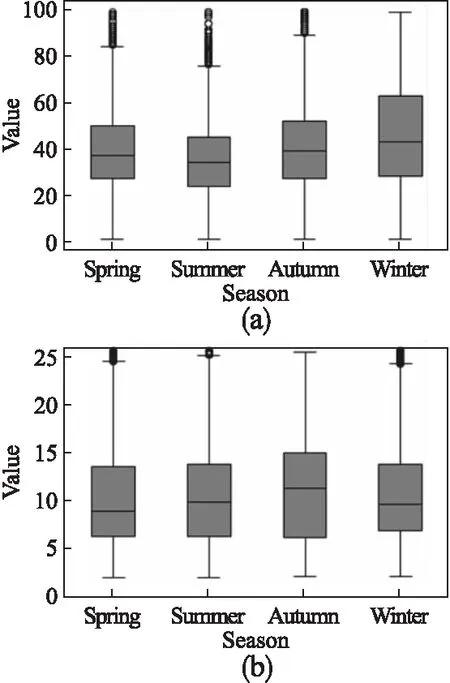
圖3 業務過程活動持續時間分析Fig.3 Business process activity duration analysis

圖3(a)表示企業在不同季節采購面料的時間分布,圖3(b)圖表示用戶在不同季節騎行的時間分布.從圖中可粗略估計,數據集1中,冬季訂購面料所需要的時間比夏季要多;數據集2中,秋季騎行時間比冬季要長.通過對數據集的分析與探索,我們發現活動時間隨著不同季節呈現出季節性變動規律;另一方面,根據經驗所得,在不同季節中,這兩種活動時間都會受到一定影響.因此在本文中考慮上下文場景為時間因素,且主要研究季節因素的影響.

根據季節效應的特性,我們將n取值為4,得US={US1,US2,US3,US4},U={U1,U2,U3,U4},E={E1,E2,E3,E4},令A=U1,B=U2,C=U3,D=U4,E=E1,F=E2,G=E3,H=E4,σE=σE1,σF=σE2,σG=σE3,σH=σE4,其中ABCD表示四季所對應的用戶隱特征矩陣,EFGH表示四季所對應的時間偏差矩陣.

假設用戶與物品之間存在的時間偏差受不同季節的影響,通過3.4.2小節中聯合概率矩陣分解模型推導過程將不同季節的用戶與物品的關系矩陣的分解、夏季用戶與物品的關系矩陣的分解、秋季用戶與物品的關系矩陣的分解以及冬季用戶與物品的關系矩陣的分解結合起來,取后驗分布函數的對數函數滿足公式(16).

(16)

最大化方程(16)并根據SGD得各部分隱特征向量迭代公式:

(17)

(18)

(19)

(20)

(21)

4.3 評價指標

本文使用均方根誤差(Root Mean Squared Error,RMSE)作為評測指標.RMSE計算實際觀測值與預測值之間的標準差,其值越小表示模型預測的結果要好.計算公式如下:

(22)

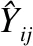
4.4 方法比較

為了驗證RCPMF方法的預測精度,將該方法與一些時間預測方法進行比較.在本文中使用歷史平均值(Mean Value,MV)方法、移動平均(Moving Average,MA)方法、指數平滑(Exponential Smoothing,ES)方法、K近鄰(k-Nearest Neighbour,KNN)方法、線性回歸(Linear Regression,LR)以及支持向量回歸(Support Vector Regression,SVR)方法與所提出RCPMF模型進行比較.為了驗證模型的效果,我們將訓練集與測試集分別按照8:2、6:4、4:6以及2:8進行劃分[15].另外,實驗過程部分放置在GitHub(1)https://github.com/woyaogithub/Collective-probabilistic-matrix-factorization.git.

4.5 迭代次數分析

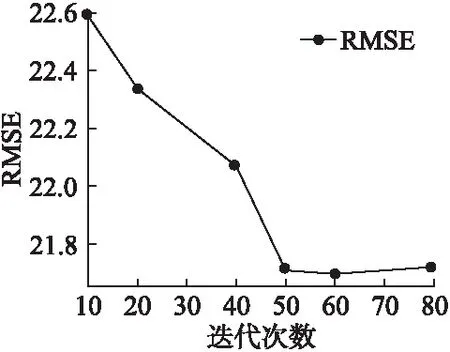
圖4 不同迭代次數的RMSE值(數據集1)Fig.4 RMSE values for different iterations(data set 1)

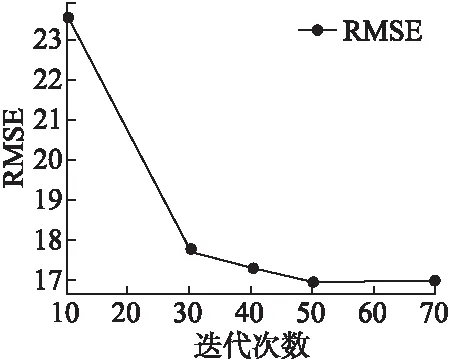
圖5 不同迭代次數的RMSE值(數據集2)Fig.5 RMSE values for different iterations(data set 2)

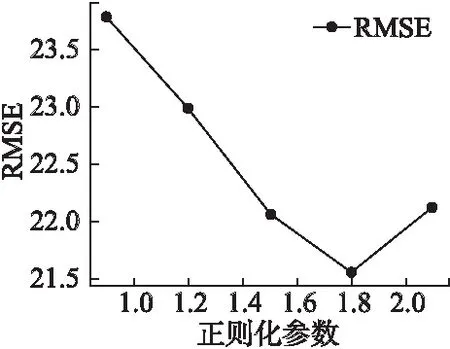
圖6 不同正則化參數值的RMSE值(數據集1)Fig.6 RMSE values for different regularization parameter values(data set 1)

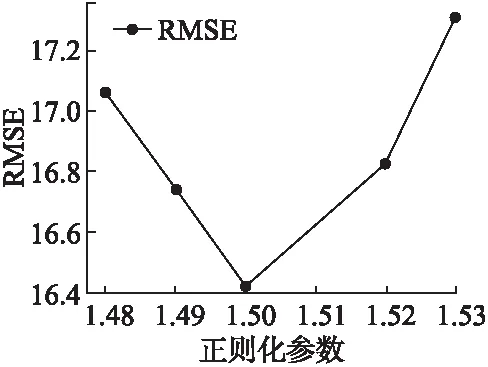
圖7 不同正則化參數值的RMSE值(數據集2)Fig.7 RMSE values for different regularization parameter values(data set 2)

在聯合概率矩陣分解部分,本文使用SGD對目標函數進行求解,因此在本節分析迭代次數對RCPMF模型的影響.為了實驗方便,在后續實驗中設置λF、λG、λH、λA、λB、λC、λD與λ值相同.

在數據集1中,我們將訓練集與測試集按照8:2進行劃分.通過多次實驗,設置學習速率α=0.001,潛在特征向量維數d=5,參數λ設置為由4.5小節得到的實驗結果.迭代次數對預測精度的影響如圖4所示.

如圖4所示,橫坐標表示算法迭代的次數,縱坐標表示RMSE值.由圖可知,隨著迭代次數的增加,算法的RMSR值下降并趨于平穩,說明我們的算法達到了收斂狀態.故在后面的實驗,我們均選擇迭代次數的值為50.

在數據集2中,我們同樣將訓練集與測試集按照8:2進行劃分.通過多次實驗,設置學習速率α=0.0005,潛在特征向量維數d=5,參數λ設置為由4.5小節得到的實驗結果.迭代次數對預測精度的影響如圖5所示.

如圖5所示,橫坐標表示算法迭代的次數,縱坐標表示RMSE值.由圖可知,隨著迭代次數的增加,算法的RMSE值下降并趨于平穩,說明我們的算法達到了收斂狀態.同樣,我們也選擇50作為后面實驗的迭代次數值.

4.6 正則化參數分析

正則化參數用來防止模型過擬合,所以正則化參數值的選擇對模型預測的精度具有很大影響.在數據集一中,我們選擇與4.4小節中相同的的數據集與參數值.正則化參數λ的對預測精度的影響,如圖6所示.

根據圖6觀察可知,正則化參數λ的值對預測時間的精度有著一定的影響.在[0.9,1.8]范圍內,隨著λ值的增加,模型預測的RMSE值呈下降趨勢,但是,當λ的值超過1.8以后,模型預測時間的RMSE值開始增加.因此,在第一個數據集中,我們將正則化參數λ設置為1.8.

同樣,在第二個數據集中,我們選擇與4.4小節中相同的的數據集與參數值.正則化參數λ的對預測精度的影響,如圖7所示.

根據圖7觀察可知,正則化參數λ的值對預測時間的精度有著一定的影響.在[1.48,1.5]范圍內,隨著λ值的增加,模型預測的RMSE值呈下降趨勢,但是,當λ的值超過1.5以后,模型預測時間的RMSE值呈上升趨勢.因此,在第二個數據集中,我們將正則化參數λ設置為1.5.

4.7 對比實驗分析

本節主要比較本文所提出的RCPMF算法與對比算法的預測效果,從實驗數據隨機抽取20%、40%、60%以及80%的訓練集對算法進行實驗.數據集1實驗結果如表2所示,數據集2實驗結果如表3所示.

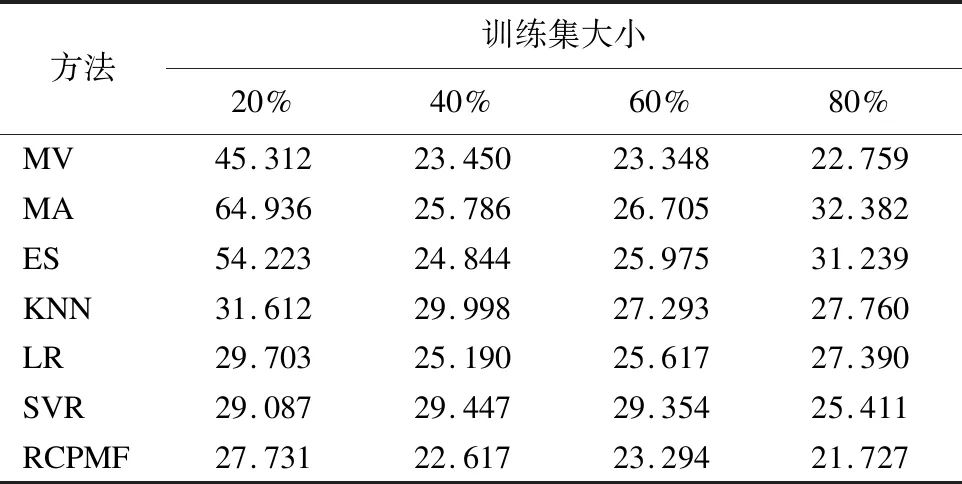
表2 不同預測方法的RMSE值(數據集1)Table 2 RMSE values for different prediction methods(data set 1)

由表2和表3所示,隨著訓練集的增大,本文所提出的方法在兩個數據集中均比其對比算法的的精度高.另外,隨著訓練集的數目增大,訓練模型預測的效果的精度呈上升趨勢.其中,在數據集1中,模型預測最好的情況下,其RMSE值比其他方法降低了1.032～10.654;在數據集2中,模型預測最好的情況下,其RMSE值比其他方法降低了4.305～13.336.通過上述分析,模型在數據集1中所取的最好結果參數組合為:訓練集與測試集比例為8:2,迭代次數值為50,學習速率值為0.001,正則化參數值為1.8;模型在數據集2中所取的最好結果參數組合為:訓練集與測試集比例為8:2,迭代次數值為50,學習速率值為0.0005,正則化參數值為1.5.

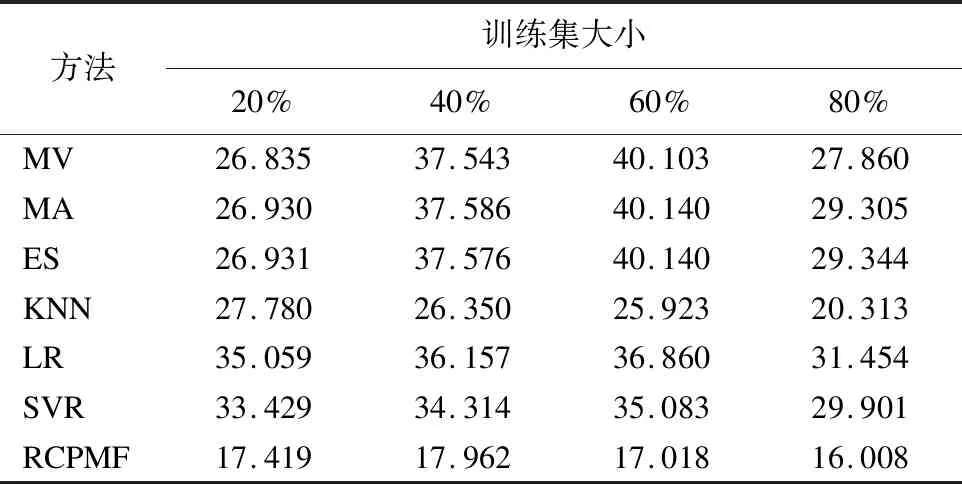
表3 不同預測方法的RMSE值(數據集2)Table 3 RMSE values for different prediction methods(data set 2)

5 總結與展望

本文結合回歸技術與聯合概率矩陣分解模型提出了一種應用于不同上下文場景下的時間預測方法.在考慮上下文場景為時間因素且分析季節因素影響的條件下,結合業務過程活動在執行過程中可觀測特征部分與不可觀測特征部分進行時間預測.通過對數據集不同程度的劃分并將本文提出的算法與相關業務活動時間預測方法進行比較,在以RMSE作為評價指標的前提下,發現該算法具有更高的預測精度.本文所提出的模型為預測活動的執行時間,所以下一步我們會考慮以該模型為基礎,將當前預測的活動時間及其自身屬性添加到特征信息列表中,在此基礎上對該業務過程的下一個活動執行時間進行預測,通過此方法以達到預測業務過程的剩余執行時間的目的.