EXCEL在配送路徑優化中的應用

何明宇

摘要：配送運輸由于目標客戶多，一般城市交通路線又較復雜，如何安排最佳配送路線是非常有挑戰性的一項工作，配送路徑優化的基本問題往往可以簡化為旅行商問題。本文的目的是展示如何在MS Excel中使用VLOOKUP和INDEX函數，結合“規劃求解”工具中的Alldifferent約束建立旅行商問題型的配送路徑優化求解模型的一種方法，并用實例說明了方法的操作過程及有效性。

Abstract： ?Due to the large number of target customers and the complicated urban traffic routes， how to arrange the best delivery route is a very challenging task. The basic problems of distribution route optimization can often be simplified to the traveling salesman problem. The purpose of this paper is to show a method to use the VLOOKUP and INDEX functions in MS Excel to establish a traveling salesman problem-based distribution path optimization solution model by combining the Alldifferent constraint in the "Solver" tool， and illustrate the operation and effectiveness of the method with examples.

關鍵詞：配送;旅行商問題;Alldifferent

Key words： distribution;traveling salesman problem;Alldifferent

中圖分類號：F253.9 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1006-4311（2019）27-0216-03

0 ?引言

王之泰教授從資源配置的角度定義“配送是以現代送貨形式實現資源的最終配置的經濟活動。”這一定義認為是配送的主要經濟活動是以現代生產力、勞動手段支撐的，依靠科技進步的，使“配”和“送”有機結合的一種送貨方式。

在配送過程中，由于配送客戶多，城市交通道路縱橫交錯，相當復雜，配送路線安排是否得當，不僅影響物流成本和車輛的運行時間，還與城市交通壓力息息相關。以往配送員大抵是依據經驗和城市布局安排的配送路線，缺乏系統的科學理論和技術指導，配送效率和經濟性都還有非常大的提升空間。

城市配送的基本問題可以簡化為一輛車從一個配送中心出發為若干需求點的客戶送貨，在現有的城市路網中，選擇合適的線路，安排一個最恰當的順序完成所有客戶的送貨，從而達到既能按時完成任務，同時總成本最小，因此配送路徑優化的基本問題又可以簡化為旅行商問題。

1 ?旅行商問題（Traveling salesman problem，TSP）

旅行商問題（TSP）是運籌學領域的一道經典名題。其一般描述為：有一名旅行推銷商人，從某個城市出發，要訪遍若干城市各一次且僅一次，最后返回到原出發城市，已知從城市i到j的旅費為Cij，問這名旅行推銷商人應該如何安排旅行路線使總旅費最少？

2 ?TSP模型的數學描述

若僅考慮前三個約束條件簇，則是類似于指派問題的模型。對TSP模型只是必要條件，并不是充分。例如，六個城市的旅行路線若為2-1-6-2和5-4-3-5，則該路線雖然滿足前三個約束條件，但是不構成整體巡回路線，它含有兩個子巡回，因此需要增加“不含子巡回”的約束條件。

3 ?文獻綜述

TSP模型是一個重要的組合優化問題，屬于NP-完全問題。迄今為止，仍然沒有找到求解它的多項式時間算法，文獻[1，2]認為，TSP不能用精確算法得到最優解，甚至得到其近似解也是不容易的。

縱觀近幾年的研究成果，研究人員解決TSP的研究方法可以歸為以下幾類，如圖1所示。

這些解法都需要在專門的軟件平臺中編程，對一般管理人員來講有一定的難度，文獻[3]基于TSP的混合整數規劃模型，并用EXCEL軟件來求解，該方法的優點是不需要專門的商業軟件和高深的編程知識，但是為了避免形成子回路引入虛擬變量ui，uj構建約束條件簇：ui-uj+nxijn-1（1i≠jn），ui，uj為常數（i，j=1，…，n）。一方面，對于大多數人來說都難以理解它的數學原理。另外，在建模時，這一約束條件也不容易被表示，且隨著模型節點數的增加，約束條件數增加非常快，大大增加模型的復雜度。

本文的目的是展示如何在MS Excel中應用VLOOKUP和INDEX函數，結合規劃求解工具中的Alldifferent約束建立旅行商問題（TSP）的模型并求出最優解，該方法的實際意義是可以為目前城市配送路線的優化問題提供一種快速有效的求解方法。

4 ?利用Excel求解器優化城市配送路徑

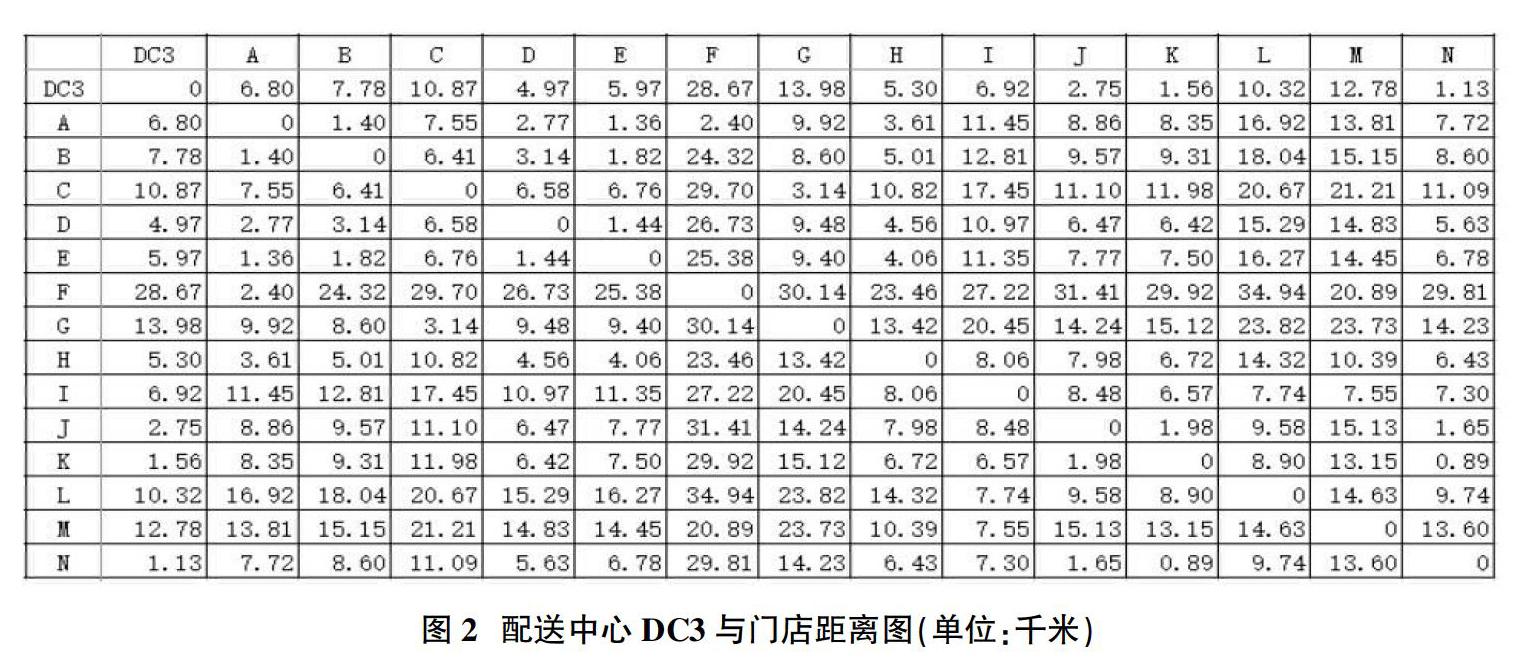
案例：HQ便利連鎖超市是四川省內的一家A股上市公司。公司現建有三座配送中心，為全市2900家連鎖超市統一配送貨物。根據門店需求信息，第三配送中心DC3需要安排一輛車為周邊14家門店進行補貨，DC3與14家門店的距離矩陣如圖2所示，如何設計配送路線才能使得車輛從配送中心DC3出發，配送完畢后返回到DC3所經過的路程最短？

4.1 EXCEL建模知識準備

4.1.1 VLOOKUP

VLOOKUP 是 Excel 中最常用且最有用的函數之一，用于在表格或區域中按行查找項目。VLOOKUP 的語法如下：

VLOOKUP（lookup_value，table_array，col_index_num，[range_lookup]）

其中：

lookup_value：必需。查閱值;

table_array：必需。包含查閱值的區域;

col_index_num：必需。包含返回值的區域中的列號;

range_lookup：可選。TRUE為近似匹配，FALSE為精確匹配。

4.1.2 INDEX

INDEX 函數返回表格或區域中的值或值的引用。使用 INDEX函數有兩種方法：數組形式和引用形式。本文的模型需要返回指定單元格或單元格數組的值，故選用數組形式。其語法如下：

INDEX（array， row_num， [column_num]）

其中：

array：必需。單元格區域或數組常量;

row_num：必需。選擇數組中的某行，函數從該行返回數值;

column_num：可選。選擇數組中的某列，函數從該列返回數值。

4.1.3 Alldifferent

一種特殊類型的整數約束（稱為“不同”約束），其中n個決策變量的值必須是從1到n的整數排列。主要應用于涉及確定最佳排序類問題。

4.2 建立配送路徑優化的EXCEL模型，如圖3所示

步驟1：對配送中心及門店進行順序編號，即D3：R3，B5：B19區域中的數字。輸入配送中心DC3與14家門店的距離矩陣。

步驟2：確定決策變量和初始可行解。

從配送中心DC出發，因為可行的次序都要求要訪遍所有門店各一次且僅一次，最后返回原出發地，因此，我們選擇編號為0的配送中心DC作為起點。

C23：C36區域為決策變量，顯示途中的旅程，以數字的次序對配送中心和門店進行排序。當我們抵達第n-1個節點時，必須要回到編號為0的配送中心，所以單元格C37并不是決策變量。

我們設單元格B23為0，無論你選擇那一家門店，從編號為0的配送中心到它之間的距離就是C23中的變量，由于要確保這家門店變成下一行程中的“起始”門店，所以在單元格B24中設置公式“=C23”，向下復制填充至B37單元格。

步驟3：建立目標函數。

在單元格D23中輸入公式“=INDEX（$D$5：$R$19，B23+1，C23+1）”，該公式的目的是從距離表中查詢出從一個節點i出發去到另一節點j走過的路程，然后向下復制填充至D37單元格。

在單元格D38中輸入公式“=SUM（D14：D19）”，用于計算走完全部門店后回到配送中心的總路程，它將作為規劃求解的目標單元格。

步驟4：將這些節點編號的數值轉換成配送中心或門店名稱。在單元格F23中輸入公式“=VLOOKUP（B23，$B$5：$C$19，2）”，然后向下復制填充至單元格F37。在單元格G23中輸入公式“=VLOOKUP（C23，$B$5：$C$19，2）”，然后向下復制填充至單元格G37。

4.3 設置規劃求解參數

選中D38單元格，點擊數據|規劃求解，打開“規劃求解參數”對話框，在“設置目標”文本框中輸入D38，選中“最小值”單選按鈕，在“可變單元格”文本框中輸入C23：C36。

單擊“添加”按鈕，打開“添加約束”對話框添加約束條件，本例中所包含的約束條件如下：

條件1：C23：H36=ALLDifferent（不含子巡回）

因為模型為非光滑規劃求解問題，故求解方法應選擇“演化”，規劃求解參數全部設置完畢，如圖4所示。

4.4 求解模型

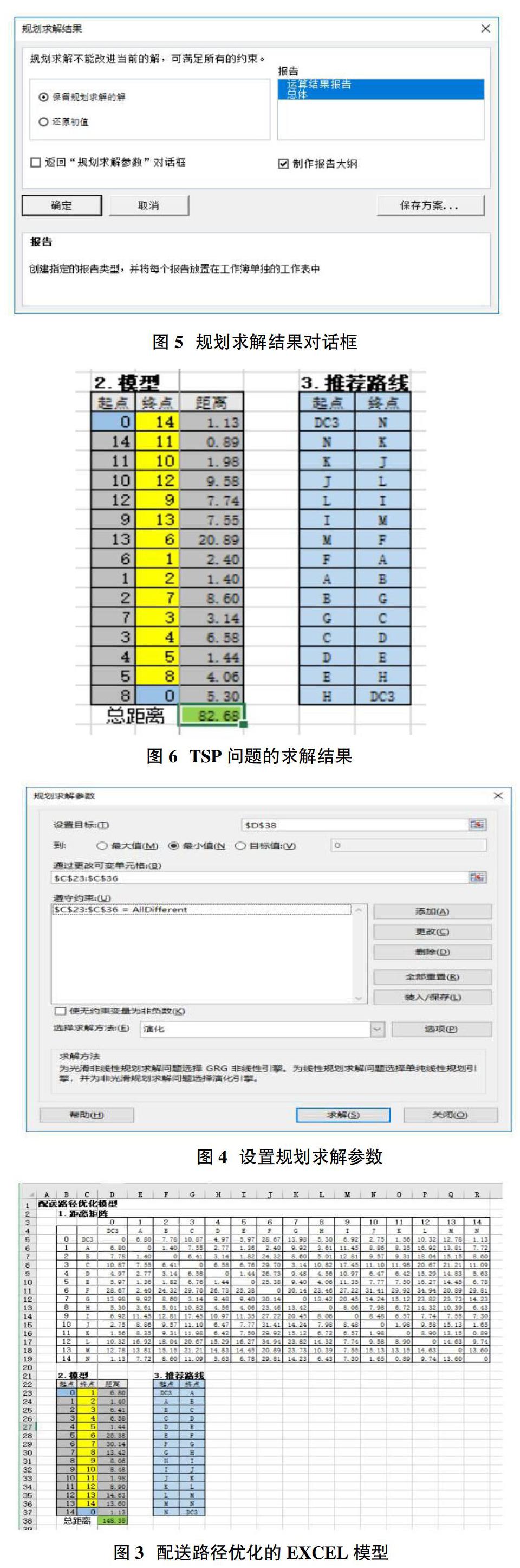
單擊“規劃錄解參數”對話框中的“求解”按鈕開始求解運算。在“規劃求解結果”對話框中并顯示找到一個最優結果，如圖5所示。

單擊的“確定”按鈕可以保存求出的最優結果，如圖6所示。

通過圖5中的可以看出，求得的最優路徑為：DC3→N→K→J→L→I→M→F→A→B→G→C→D→E→H→DC3，配送車輛行駛的總里程為82.68千米。

5 ?結論

①盡管有許多學者利用專業軟件對旅行商問題建立了較為系統的算法模型，但是，實際應用中經常遇到許多問題，如需要專業軟件環境支持，軟件費用昂貴，操作員專業化程度要求很高等。

②靈活運用Excel結合其強大計算能力建立了配送管理中路線優化決策中的基本問題——TSP的ECXCEL模型，為該類問題的求解提供了一種有效的思路。該方法在配送和運輸物流領域具有重要的實際意義。

③模型求解花費時間： 89.187 秒。表明使用該模型求解一般的路線優化問題快速且高效。需求地的增加成倍地增加了（尋找最佳行走路線）任務的復雜性，使用MS Excel 規劃求解工具可以很容易地解決TSP類型的配送路徑優化問題，而不用擔心客戶的數量。

參考文獻：

[1]徐麗蕊.城市配送TSP問題的LINGO求解[J].電子設計工程，2015，23（13）：62-64.

[2]嚴晨，王直杰.以TSP為代表的組合優化問題研究現狀與展望[J].計算機仿真，2007，24（6）：171-174.

[3]張敏，金琴玲.旅行商問題的一種新解法[J].重慶職業技術學院學報，2008（1）：153-154.

[4]戴宗瑞.TSP問題在物流配送車輛運行路線中的應用分析[J].軟件導刊，2012，11（6）：93-95.

[5][美]Michael R.Middleton.使用Microsoft Excel進行數據分析[M].北京：中國水利水電出版社，1997.

[6]ExcelHome. Excel 2010數據處理與分析實戰技巧精粹[M].北京：人民郵電出版社，2014，1.

[7]王劍文，戴光明，謝柏橋，張全元.求解TSP問題算法綜述[J].計算機工程與科學，2008，30（2）：72-74.

[8]潘正君，康立山，陳毓屏.演化計算[M].北京：清華大學出版社，1997.