高精度引信的LMS 濾波與WVD 算法實現(xiàn)

張鳳萍, 劉亞奇, 梁 影, 倪 亮

(上海無線電設(shè)備研究所,上海201109)

0 引言

引信處理對象的信噪比會隨著探測距離的增加而降低,因此需要對引信目標信號進行濾波降噪。自從Windrow等人提出自適應(yīng)信號處理方法后,自適應(yīng)技術(shù)就廣泛應(yīng)用在通信、雷達等領(lǐng)域[1-2]。相對于諸如維納濾波器等的傳統(tǒng)濾波器,自適應(yīng)濾波器通過自動迭代調(diào)節(jié)自身的參數(shù),實現(xiàn)較好的濾波性能[3-6]。本文將自適應(yīng)濾波技術(shù)引入到引信接收機信號預(yù)處理系統(tǒng)中。

數(shù)字信號處理系統(tǒng)通常使用快速傅立葉變換(FFT)獲取信號的頻域信息。然而,傅立葉變換不能判斷出任意時刻信號的頻率信息變化。而實時系統(tǒng)中的信號一般會隨著時間的變化而變化,系統(tǒng)需要根據(jù)任意時刻的信號時頻信息及時地做出相應(yīng)的反應(yīng)。時頻分析是一種非平穩(wěn)信號的處理手段,可求出任意信號時間和頻率的聯(lián)合函數(shù),描述信號在不同時間的頻率和幅度信息變化[7-9]。

本文以引信接收機輸出信號的實時濾波與幅頻定距為研究內(nèi)容。為了改善引信定距精度,提出了一種自適應(yīng)濾波處理與時頻特征提取的引信信號處理方案。

1 FPGA+DSP的結(jié)構(gòu)設(shè)計

考慮到現(xiàn)場可編程邏輯門陣列(FPGA)的并行處理速度快,算法結(jié)構(gòu)簡單等特點,底層信號預(yù)處理模塊使用FPGA實現(xiàn)。數(shù)字信號處理器(DSP)算法設(shè)計較靈活,能實現(xiàn)較復(fù)雜的數(shù)字信號處理,高層信號特征提取模塊使用DSP實現(xiàn)。引信信號處理實時性要求高,算法實現(xiàn)較復(fù)雜,本文提出基于DSP+FPGA結(jié)構(gòu)的信號處理方案。在算法實現(xiàn)效率和運算速度等方面具有優(yōu)勢,DSP+FPGA的結(jié)構(gòu)十分適合引信信號處理部分的實現(xiàn)。

FPGA+DSP結(jié)構(gòu)的引信幅頻定距框圖如圖1所示。為了實現(xiàn)更高的定距精度,需要對取樣積分處理后的接收機信號進行放大濾波和特征提取。圖中采用FPGA實現(xiàn)最小二乘法(LMS)自適應(yīng)濾波算法,完成信號濾波;采用DSP實現(xiàn)維格納-威利時頻分布(WVD)算法,完成信號的時頻分析;“幅頻定距控制”給出系統(tǒng)下一級的啟動信號。

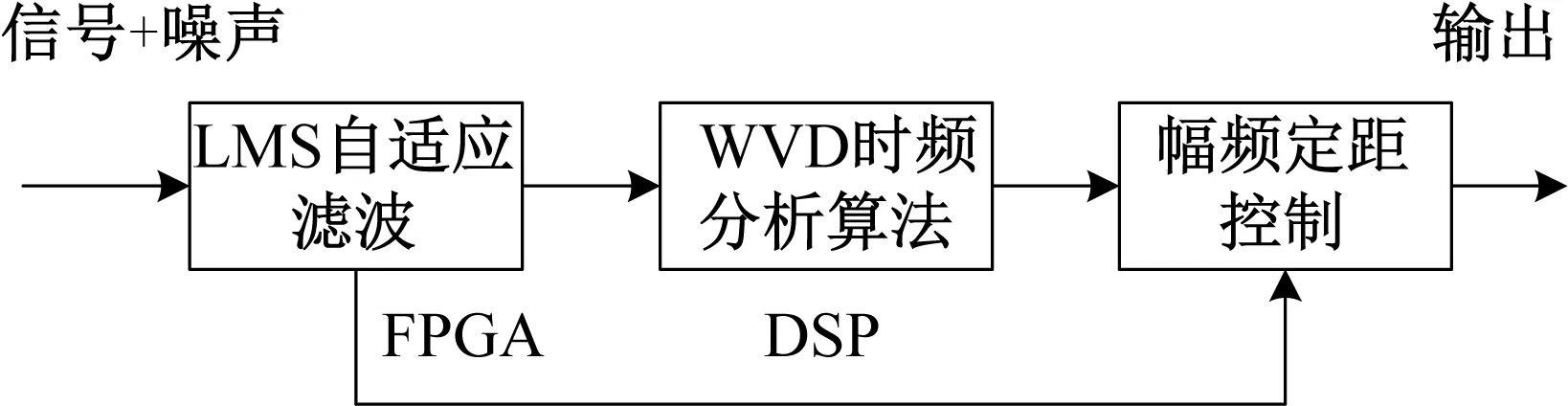
圖1 FPGA+DSP結(jié)構(gòu)的幅頻定距框圖

基于FPGA對自適應(yīng)濾波算法進行實現(xiàn)時,濾波結(jié)構(gòu)系數(shù)的量化會引起一定誤差。為了滿足系統(tǒng)頻率的辨識精度,盡可能減少計算資源的消耗,系數(shù)被量化為12位,系統(tǒng)頻率響應(yīng)的偏移不大于60 d B。計算階次越大,所需乘法次數(shù)越多,乘法運算的舍入誤差對輸出影響越大,該LMS濾波算法采用的計算結(jié)構(gòu)只有七階。信號處理時,輸入輸出數(shù)據(jù)一律進行了16位的數(shù)字量化,必要時可實施字擴展和字截取,滿足系統(tǒng)精度要求。

在WVD算法實現(xiàn)時,為了對信號進行不同時間點的特征提取,需要對信號序列進行分段截取。每等待一定的時間,進行一次數(shù)據(jù)采集。而等待的時間點數(shù)多少會影響信號特征提取的反應(yīng)速率。設(shè)計每次截取長度為256個點,每等待64個點截取一次數(shù)據(jù)進行WVD變換。

2 LMS自適應(yīng)濾波處理

使用MATLAB R2014a(32-bit)數(shù)值仿真軟件和ModelSim ALTERA 10.1 d硬件功能仿真軟件,對固定系數(shù)有限沖擊響應(yīng)FIR濾波器和系數(shù)自動調(diào)整的自適應(yīng)濾波器進行了性能仿真對比。對比結(jié)果表明,固定系數(shù)的FIR濾波器在改善濾波效果時需要人工調(diào)整系數(shù)。最優(yōu)系數(shù)確定比較困難,調(diào)整效率低。而自適應(yīng)濾波器能適應(yīng)不同的輸入信號,較快地實現(xiàn)輸入信號的理想濾波。

采集21組引信輸入信號,分別進行LMS自適應(yīng)濾波仿真與硬件實現(xiàn)。式(1)引入了參數(shù)Is,用來度量算法對信號的濾波程度,該參數(shù)值越小,則算法的濾波效果越強。式(2)引入了歸一化均方誤差(NMSE),同樣地度量算法對信號波形的改變程度,其值越大表示波形改變越大,最小為0,表示算法對波形沒有改變。

濾波系數(shù)Is與歸一化均為誤差e分別為

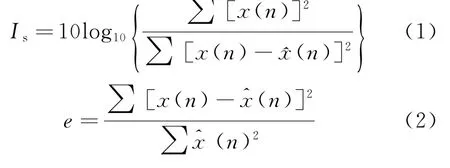
式(1)與式(2)中：x(n)為輸入信號;^x(n)為濾波后輸出信號。將濾波后輸出信號^x(n)近似為理想信號,輸入與輸出的差值x(n)-^x(n)近似為噪聲。

濾波結(jié)果如圖2所示。由圖2(a)可以看出,根據(jù)MATLAB仿真結(jié)果與FPGA實測結(jié)果計算得到的Is參數(shù)曲線基本重合,表明硬件能較好地實現(xiàn)該LMS自適應(yīng)濾波,Is保持在3 dB左右。

同樣,圖2(b)中 MATLAB的仿真計算與FPGA的自適應(yīng)濾波得到的NMSE也基本一致,濾波算法能較好地完成信號雜波的去除,NMSE參數(shù)可達0.45。Is與NMSE參數(shù)值均波動較小,濾波算法針對不同的引信信號性能表現(xiàn)穩(wěn)定。

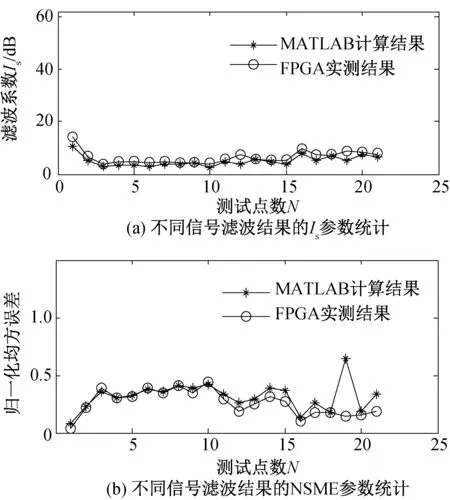
圖2 21組引信信號濾波效果

3 WVD時頻特征提取

傳統(tǒng)的FFT算法,對時頻特征引入柵欄效應(yīng),導(dǎo)致時頻分布模糊。對引信接收機輸出分別進行短時傅立葉(STFT)和WVD時頻變換。無論是仿真結(jié)果還是實測結(jié)果,STFT算法的頻譜泄漏較嚴重。WVD時頻分布中,諧波分布比較集中,計算結(jié)果在時間和頻率軸上的定位都比較準確。相對于STFT算法,WVD算法更能準確進行時頻特征識別。

圖3是采用DSP實現(xiàn)的WVD時頻分布結(jié)果。可以看出,從0.143 s到0.154 s,信號在1 k Hz～5 k Hz頻率范圍內(nèi)的諧波幅度逐漸增強到最大,并趨于穩(wěn)定。在回波信號強度達到最大時,WVD時頻分析的1 k Hz～5 k Hz諧波強度最高,能保證幅度最高點定距起爆條件。以MATLAB仿真計算結(jié)果為參照,采用DSP能較好地實現(xiàn)WVD算法。硬件處理引入的系統(tǒng)誤差對定距控制的影響在可接受范圍內(nèi)。對引信信號來說,DSP實現(xiàn)的WVD時頻分析算法可以較好地反應(yīng)輸入信號的幅頻變化趨勢,有利于對精確定距的控制。

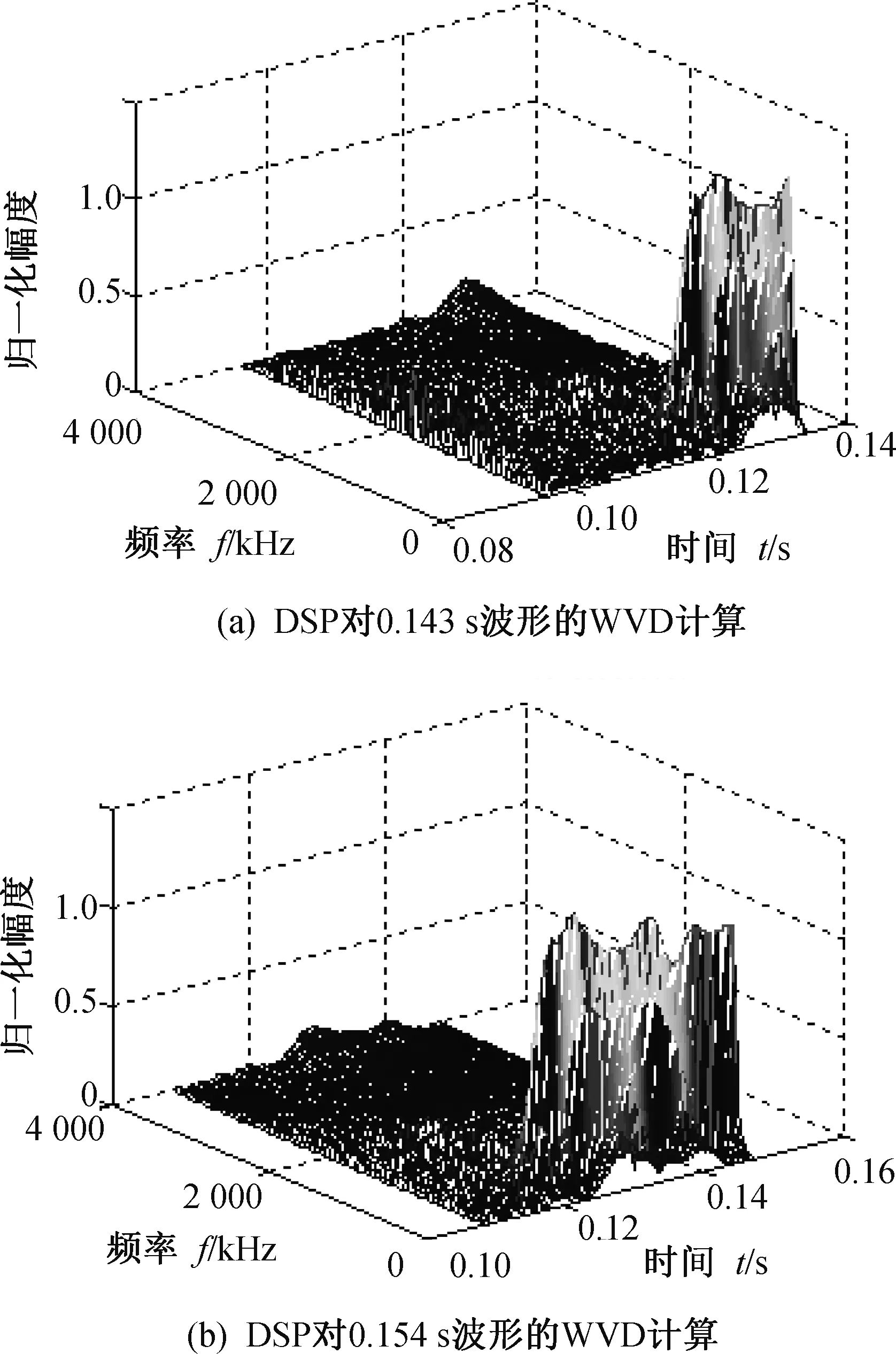
圖3 定距前后采樣波形的WVD時頻分析

4 引信信號的幅頻定距測試

能量檢測算法不考慮信號的波形參數(shù),通過計算信號在一段時間內(nèi)的能量累積進行定距判別。本文計算了自適應(yīng)濾波后的信號平均功率與總能量,并根據(jù)當前時刻的信號大小與之前信號幅度波動的標準差,自適應(yīng)地調(diào)整平均功率判別閾值。然后綜合WVD算法計算得到的信號幅頻特征,進行信號時域與頻域的聯(lián)合定距判別。預(yù)處理模塊對引信測試信號進行自適應(yīng)濾波,給出第一個定距判定結(jié)果。采用DSP完成信號時頻計算,判別當前時刻波形的幅頻特性是否滿足定距要求,滿足則給出第二個定距判定結(jié)果。只有兩個定距判定結(jié)果都滿足起爆條件時,才啟動下級電路。

由于彈體飛行速度可以根據(jù)經(jīng)驗由引信信號頻率得出,定距精度則可以由定距時間誤差與信號周期的比值求出。對算法進行定距精度測試時,通過統(tǒng)計定距啟動時刻的定距標準差與信號周期的百分比,間接度量定距算法的定距精度。對不同組引信信號進行定距測試時,每組信號分別添加不同強度的高斯白噪聲,多次重復(fù)完成測試。計算結(jié)果見表1。

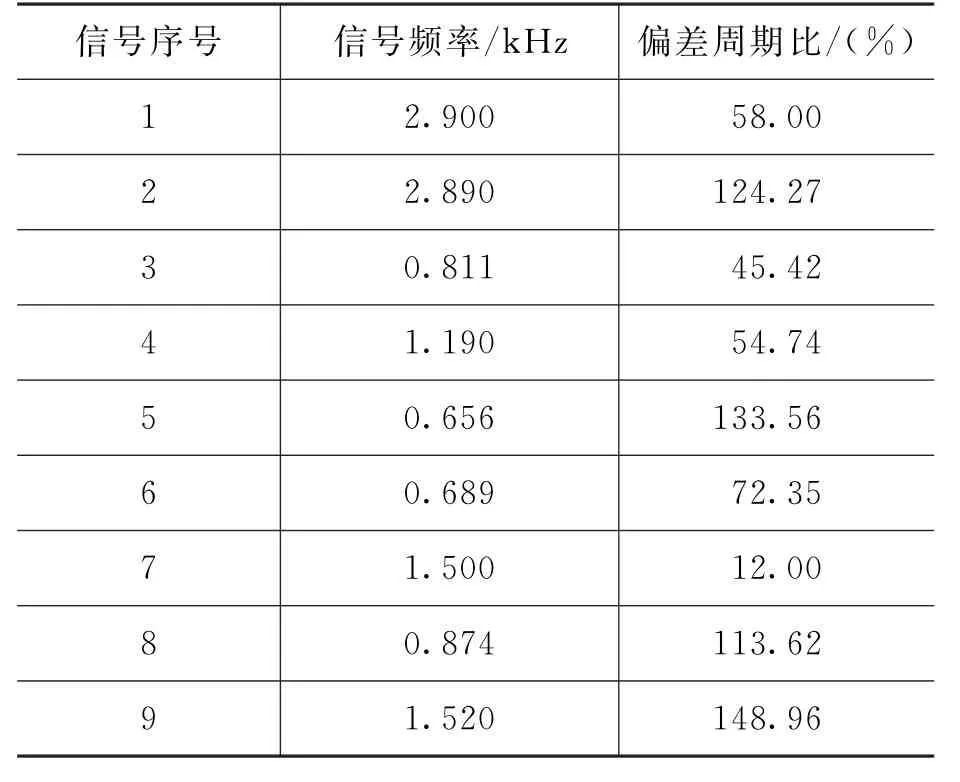
表1 九組信號定距測試統(tǒng)計

偏差周期比越大,噪聲強度不同時,算法對同一信號的定距偏差越大。定距偏差周期比最大約150%,即定距時間誤差最大是信號周期的1.5倍。由經(jīng)驗公式計算可知,當前算法的定距精度小于10 cm,甚至更高。對不同組信號進行定距測試,定距結(jié)果穩(wěn)定。

5 結(jié)論

采用FPGA實現(xiàn)的自適應(yīng)濾波算法性能穩(wěn)定,濾波后信號信噪比明顯改善,雜波分量減少,有利于幅度峰值的定距判別。采用DSP實現(xiàn)的WVD時頻分析能較好地完成引信信號的時頻域特征提取,有利于幅頻定距算法從頻域上給出定距判定結(jié)果。幅頻定距測試結(jié)果顯示,算法在最大幅度值處給出定距啟動信號,并保證信號的定距偏差是信號周期的10%～150%之間,定距精度高于10 cm。