基于GANPSOBP神經網絡的糧情預測模型研究

郭平飛 甄彤

摘 ?要： 在使用BP神經網絡構建糧情溫度預測模型時，因其存在誤差高、穩定性差等缺陷，借鑒遺傳算法和粒子群的思想，提出一種GANPSO?BP神經網絡來預測糧食溫度。首先為驗證GANPSO算法的可用性，將該算法與PSO算法和IPSO算法在測試函數上利用Matlab軟件進行模擬測試，結果得出GANPSO算法效果相對與其他兩種算法有著明顯提高;然后再對BP，PSO?BP和GANPSO?BP三種神經網絡進行測試，得出BP的均方誤差為0.021 79，PSO?BP的均方誤差為0.017 65， GANPSO?BP的均方誤差為0.013 30;從而得到GANPSO?BP神經網絡相對于其他兩種有著較好的穩定性，能夠很好地預測糧食溫度的變化情況。

關鍵詞： 糧食溫度; 回歸預測; GANPSO?BP神經網絡; 仿真模擬; 預測分析; 權重優化

中圖分類號： TN711?34; TP301.6 ? ? ? ? ? ? ? ? ? ? 文獻標識碼： A ? ? ? ? ? ? ? ? ?文章編號： 1004?373X（2019）20?0021?05

Research on grain situation prediction model based on GANPSO?BP neural network

GUO Pingfei， ZHEN Tong

（College of Information Science and Engineering， Henan University of Technology， Zhengzhou 450001， China）

Abstract： Since the grain temperature prediction model constructed with the BP neural network has some shortcomings such as high error and poor stability， a GANPSO?BP neural network is proposed to predict the grain temperature by means of the genetic algorithm and particle swarm thought. The simulation testing of GANPSO algorithm， PSO algorithm and IPSO algorithm are conducted for their testing functions by means of MATLAB software to verify the availability of GANPSO algorithm. The results show that the predicting effect of GANPSO algorithm is improved more significantly in comparison with other two algorithms. The BP neural network， BP?GANP neural network and GANPSO?BP neural network were tested， and the mean square errors of 0.021 79， 0.017 65 and 0.013 30 were obtained respectively for PSO?BP neural network， BP neural network and GANPSO?BP neural network. ?The results show that， in comparison with other two algorithms， the GANPSO?BP neural network has better stability， and can predict the change of grain temperature much better.

Keywords： grain temperature; regression prediction; GANPSO?BP neural network; analogue simulation; predictive analysis; weight optimization

0 ?引 ?言

在糧食儲藏的過程中，糧堆中糧食受到的影響因子較多，再加上儲藏周期很長，如何提高糧食儲藏的品質和降低在儲存過程中造成的損失就顯得尤為重要。在糧食儲藏中對糧食品質有影響的因素很多[1]，如溫度、濕度、害蟲、霉菌[2]和氣體[3]等，但在這些因素中對其影響最大的是溫度。若能利用這些已測數據對糧堆內溫度進行預測就可以提前發現問題，減少糧食損失。

近些年，有很多學者對糧庫中糧食的溫度方面有所研究。如李祥利等發現利用“F”型通風道對房型倉底輸送冷風可以使倉內溫度分布均勻，減少通風死角[4]。Jian F等發現害蟲運動的速度和方向受溫度、溫度梯度、地形起伏以及溫度梯度與地形的相互作用影響[5]。張燕君等以響應面模型理論為基礎，采用有限元數值模擬的方法對大型糧倉冬夏兩季溫度分布反演了多項式的數學模型[6]。通過對這些研究現狀的了解，為建立一種新的研究思路，引入一種前饋神經網絡的方法，利用糧倉中諸多影響糧堆溫度的因素對糧堆中溫度進行分析研究。因BP神經網絡的自身缺陷，所以在對神經元的權值和閾值初始化的過程中使用GANPSO算法對其神經元的權值和閾值進行優化。

1 ?基于GANPSO?BP的糧情預測模型

1.1 ?BP神經網絡

BP（Back Propagation）神經網絡是將訓練出的所有信息以神經元節點閾值和權值的形式存放在訓練網絡中，從而使該網絡有較好的自學習效果和泛化能力。

式中：[xi]為第i個輸入;[ω]為連接權值;[α]和[β]為閾值;[Ij]為第j個隱層輸出;M和N為隱層和輸出層神經元個數;[yk]為第k個輸出層神經元的輸出;[ek]為第k個輸出層神經元的誤差值。

1.2 ?標準PSO原理

粒子群算法（PSO）是通過群體智慧來尋覓目標的最優解。在PSO算法中最為核心的就是群體中個體的位置和速度的更新，通過它們的有效更新才能完整運行整個算法。粒子第k+1次的主要更新公式如下：

式中：[ω]為慣性權重;[c1]，[c2]為加速度因子，通常情況下，加速因子為非負數;[Xin]為粒子位置;[Vin]為粒子速度;[r1]，[r2]是[0，1]之間的隨機數。

1.3 ?GANPSO算法

在面對PSO算法的尋求中，許多專家和學者都對其尋優有著自己獨特的更新方法。如吳沖等提出了一種動態調整加速因子和慣性權重的PSO算法[7];張世欽提出在慣性因子和種群拓撲這兩方面對PSO算法進行改進[8];肖理慶等提出使用區間算法、輪盤賭的方法和改進精英策略來改進PSO[9]等。

針對PSO算法的缺點，提出了新的慣性權重函數來對其進行優化，同時借助遺傳算法思想來優化PSO算法的尋優過程，從而使問題盡快得到最優。

1.3.1 ?慣性權重優化

前文已提到PSO算法可以通過對粒子的更新來尋找目標空間的最優，但是在標準PSO算法中仍舊存在著一些缺陷。針對這些問題，對粒子的慣性權重進行優化。對慣性權重[ω]改進公式為：

式中：[ωmin]和[ωmax]值分別為0.4和0.9;T為最大迭代次數;i為當前迭代次數。

1.3.2 ?遺傳算法優化

除了對慣性權重進行優化外，還可以利用遺傳算法對其尋優過程進行優化，在優化前，需要先初始化位置和速度，然后在計算適應度值（FIT值）后，才可以對粒子進行優化操作。在該算法中，適應度函數為平均絕對誤差值。

在計算出各個粒子的FIT值后，對其排序，取前一半粒子新建粒子群，并在該群中隨機取出兩個不同粒子，再對選好粒子進行交叉。若操作失敗，則放棄此次結果。交叉公式為：

除此之外，在粒子種群更新中，先隨機一個[0，1]之間的隨機數，若該隨機數大于給定的某一個值，那么決定對循環中的該粒子進行變異。變異時只變異該粒子的全部元素。同時若最優解的粒子位置數次未變，也可以變異該粒子。

當然為防止該算法再次陷入局部最優，又對其FIT值在4次未改變時，對該次的全局最優值進行變異。若變異后的FIT值不如以前，則返回先前的全局最優值。變異公式如下：

1.4 ?GANPSO?BP神經網絡

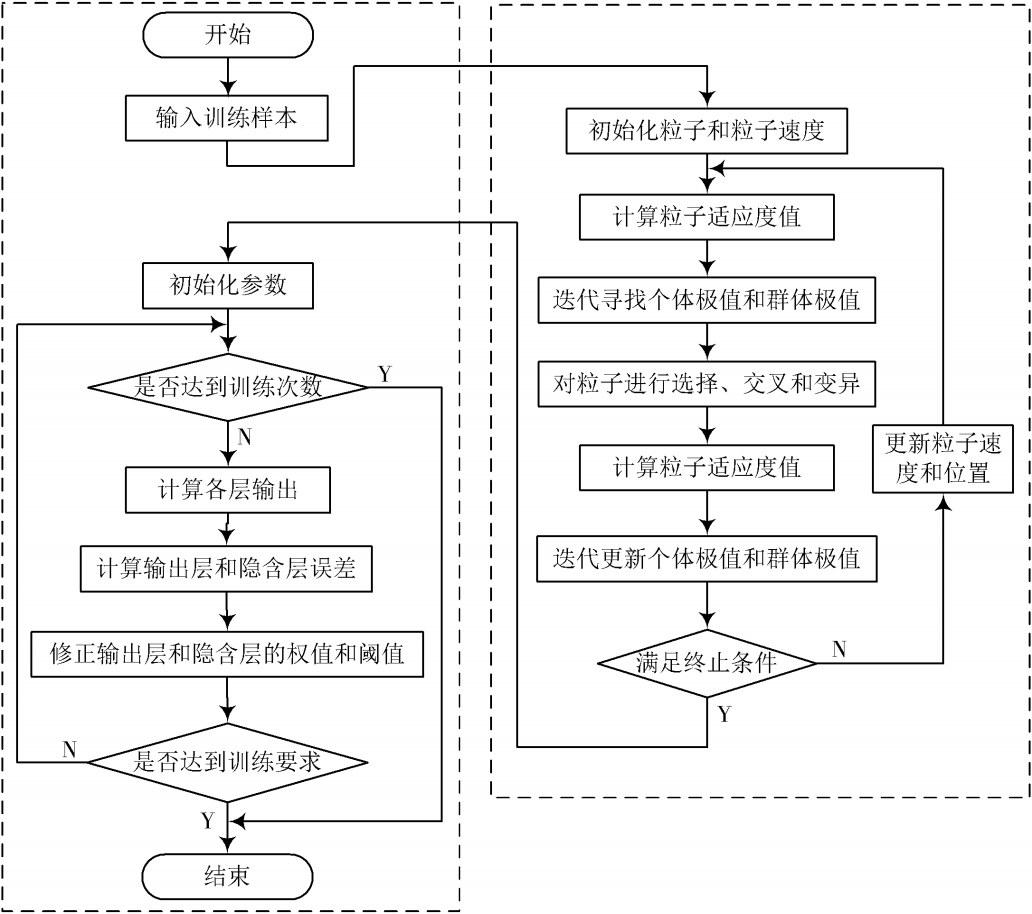
BP神經網絡在對非線性系統建模時，其初始閾值和權值都是隨機生成的，生成值不同會導致不一樣的預測結果。因此可以使用粒子群算法對其權值和閾值進行優化。在對其優化前，還需確定BP神經網絡各層的神經元數量，以便于定下PSO算法的粒子維度。在優化過程中，粒子群的適應度函數為BP神經網絡，適應度值為訓練數據的平均誤差值。GANPSO?BP算法的流程圖如圖1所示。

圖1 ?GANPSO?BP算法的流程圖

2 ?建模與仿真

2.1 ?GANPSO算法測試

2.1.1 ?測試函數

為比較PSO算法、IPSO[10]算法和GANPSO算法的性能效果，本文在CEC2014的PSO算法標準測試函數中，選取3個極值為零的測試函數。測試函數的表達式和粒子收索空間如表1所示。

2.1.2 ?算法參數選擇及測試環境

對于PSO算法和IPSO算法[10]中具體參數可以參考其文獻中設置的相應值。在GANPSO算法中，交叉操作和變異操作的概率分別為0.5和0.4。本文的測試環境是Windows 10系統，測試軟件為Matlab R2016a。

2.1.3 ?測試結果

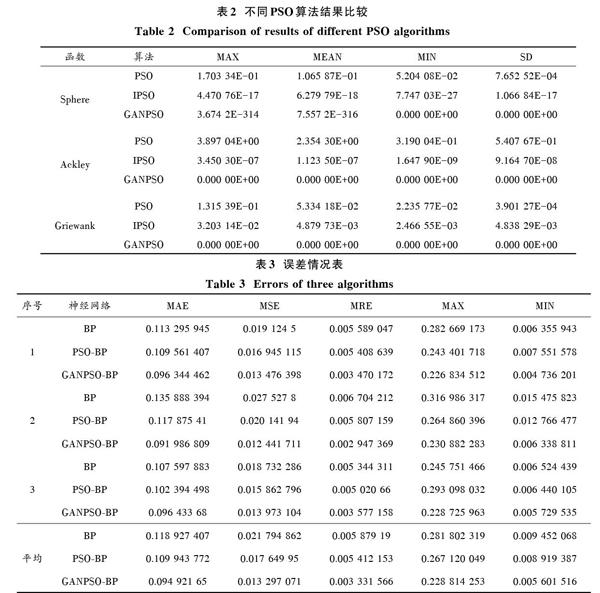
為了保證測試結果有效性和可靠性，對于每個測試這三種算法均運行50次，最后FIT的絕對值中最大值（MAX）、最小值（MIN）、平均值（MEAN）和方差（SD）的平均值作為判斷這三種算法的性能指標。不同算法比較結果如表2所示。

表1 ?測試函數

對于表2的數據，可以明顯看出在Sphere，Ackley和Griewank三個函數中，GANPSO算法要明顯強于PSO算法和IPSO算法的效果。表2中GANPSO算法的部分結果為零，并不是真的為零，而是因其值太小，軟件顯示結果為零。如在Ackley函數中，GANPSO算法在運行到146次左右時其適應度值為3.552 7×10-15。

2.2 ?糧情預測結果測試

2.2.1 ?測試數據

該算法模型的實驗樣本來自華東地區的某個糧庫，以2016年前11個月的糧倉數據來預測后1個月的溫度數據。用于預測的輸入數據有糧倉外部溫度、糧倉外部濕度、糧倉內部溫度、糧倉內部濕度和糧堆溫度。由于在本次實驗中主要預測為糧倉中糧堆的底層溫度點的平均溫度，因此期望輸出數據設置為該平均溫度3天后的溫度值。

2.2.2 ?算法參數選擇及測試環境

由于在不同輸入的參數中間可能存在著數量級的差別，所以在對實驗數據訓練前，需要對該實驗數據進行歸一化。在本文中使用的歸一化公式為：

式中：[xk]為第k個訓練數據;[xmax]為訓練參數中的最大值;[xmin]為訓練參數中最小值。

在BP神經網絡中，隱層只有一層，神經元節點數按照經驗得到節點數為3時較好。BP神經網絡的激勵函數根據實際訓練情況，發現將隱含層激勵函數設置為tan?sigmoid函數，同時將輸出層為線性函數purelin時，訓練函數為trainscg，預測效果較好。

在對糧溫的預測誤差方面主要用均方誤差（MSE）、平均絕對誤差（MAE）和平均相對誤差（MRE）來表示。

2.2.3 ?測試結果

對測試數據使用BP，PSO?BP和GANPSO?BP這三種神經網絡分別進行預測。為保證其有效性，對于每一個序號內的預測值，均為該三種神經網絡運行10次后不同誤差值的平均值。

其預測結果如表3所示。

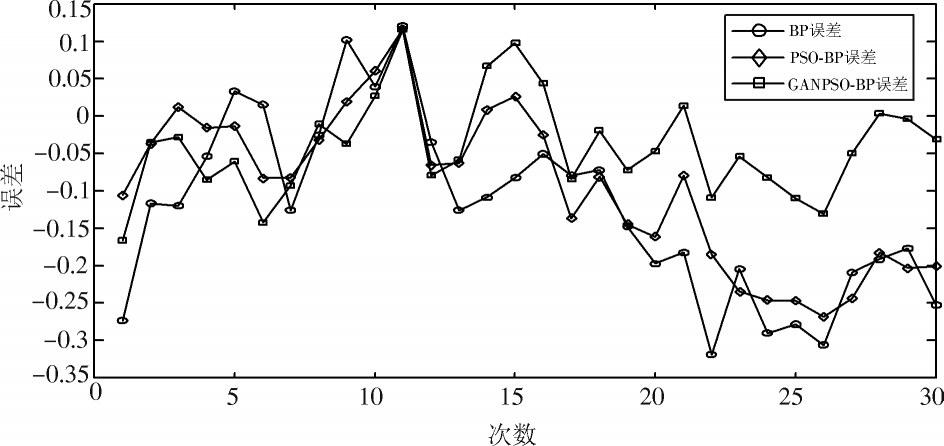
從表1中不同公式計算出來的誤差值可以看出，BP神經網絡中各項誤差值均大于通過其他方法得到的誤差值，由此可知BP神經網絡的預測效果相對較差。而使用GANPSO?BP算法的數據預測結果相對于其他方法較為理想，其誤差數值相對較小，數據變化程度較低，可信度較高。為了更能清晰地看出預測結果的不同，選取其中一次的預測溫度和誤差，用Matlab畫圖見圖2、圖3。

從圖2和圖3可以看出，使用遺傳算法和對慣性權重改進后的GANPSO?BP相對于其他兩種神經網絡，預測效果較好，絕對預測誤差值較低。GANPSO?BP較BP和PSO?BP神經網絡的預測結果最大偏差較小，穩定性較高。

圖2 ?預測溫度圖

3 ?結 ?語

對于PSO算法的優化問題，通過改變其慣性權重，而后在此基礎上使用遺傳算法中變異和交叉方法來優化其粒子更新過程。同時利用三個常用測試函數對其性能進行測試，發現GANPSO算法比IPSO算法和PSO算法的得出結果有明顯的提高。

對于糧食溫度預測問題，使用BP神經網絡、PSO?BP神經網絡和GANPSO?BP神經網絡分別預測糧倉中糧食溫度。實驗對比結果顯示，改進后GANPSO?BP比BP神經網絡和PSO?BP神經網絡測試數據的預測溫度誤差相對較小，預測穩定性更好，預測溫度精度更高。

圖3 ?預測誤差圖

參考文獻

[1] 鄧永學，趙志模，李隆術.環境因子對儲糧害蟲影響的研究進展[J].糧食儲藏，2003，32（1）：5?12.

DENG Yongxue， ZHAO Zhimo， LI Longshu. Research advance of environmental factors on stored grain insects [J]. Food storage， 2003， 32（1）： 5?12.

[2] 黃淑霞，蔡靜平，田海娟.主要糧食品種儲藏期間霉菌活動特性研究[J].中國糧油學報，2010，25（1）：99?102.

HUANG Shuxia， CAI Jingping， TIAN Haijuan. Mould development characters of different stored grains [J]. Journal of the Chinese cereals and oils association， 2010， 25（1）： 99?102.

[3] 余磊.糧倉有害氣體檢測系統的研究[D].鄭州：河南工業大學，2014.

YU Lei. Study on detection system for harmful gas in granary [D]. Zhengzhou： Henan University of Technology， 2014.

[4] 李祥利，王雙鳳，王遠成.房式倉糧堆溫度和水分變化的模擬研究[J].糧油食品科技，2012，20（3）：53?56.

LI Xiangli， WANG Shuangfeng， WANG Yuancheng. Numerical simulation of temperature and moisture in grain heap in large warehouse [J]. Science and technology of cereals， oils and foods， 2012， 20（3）： 53?56.

[5] JIAN F， JAYAS D S， WHITE N D G. Movement of adult rusty grain beetles， cryptolestes ferrugineus （coleoptera： cucujidae）， in wheat in response to 5 ℃/m temperature gradients at cool temperatures [J]. Journal of stored products research， 2003， 39（1）： 87?101.

[6] 張燕君，謝曉偉，黃寶凱，等.大型糧倉溫度分布反演數學模型的研究[J].光學技術，2012，38（3）：288?294.

ZHANG Yanjun， XIE Xiaowei， HUANG Baokai， et al. The application of fiber Bragg grating temperature testing system in the barn [J]. Optical technique， 2012， 38（3）： 288?294.

[7] 吳沖，劉佳明，郭志達.基于改進粒子群算法的模糊聚類?概率神經網絡模型的企業財務危機預警模型研究[J].運籌與管理，2018（2）：106?132.

WU Chong， LIU Jiaming， GUO Zhida. Use of hybrid fuzzy c?means and probabilistic neural network based on improved particle swarm optimization in the prediction of financial distress [J]. Operations research and management science， 2018（2）： 106?132.

[8] 張世欽.基于改進粒子群算法的風光水互補發電系統短期調峰優化調度[J].水電能源科學，2018（4）：208?212.

ZHANG Shiqin. Short?term peak shaving for wind?photovoltaic?hydro system optimization based on improved particle swarm optimization [J]. Water resources and power， 2018（4）： 208?212.

[9] 肖理慶，王化祥.利用改進粒子群算法優化ERT有限元模型[J].計算機應用研究，2017，34（5）：1581?1584.

XIAO Liqing， WANG Huaxiang. Optimization of ERT finite element model by improved particle swarm optimization algorithm [J]. Application research of computers， 2017， 34（5）： 1581?1584.

[10] 梁昔明，陳富，龍文.基于動態隨機搜索和佳點集構造的改進粒子群優化算法[J].計算機應用，2011，31（10）：2796?2799.

LIANG Ximing， CHEN Fu， LONG Wen. Improved particle swarm optimization based on dynamic random search technique and good?point set [J]. Journal of computer applications， 2011， 31（10）： 2796?2799.