基于旋轉基線的仿生學測向研究
卓欣然,王思佳,竇修全
(1.電子科技大學,四川 成都 611731;(2.中國電子科技集團公司第五十四研究所,河北 石家莊 050081)
0 引言
新世紀的戰爭已發展成為電子戰和信息戰,掌握即時信息就掌握了戰爭的主導權。無線電測向與定位是電子偵察的重要內容,首次應用于第一次世界大戰,特別是在第二次世界大戰期間,用于發現敵方潛艇艦隊方位,引導武器轟炸特定目標。隨著新型作戰樣式的出現,測向設備需要搭載到有人機、無人機等有限空間[1]。機動平臺有限的空間導致天線陣基線長度無法滿足半波長要求,按照常規測向理論,無法實現對偵察目標的有效測向。文獻[2-3]論述了仿生學的發展及應用,為其他學科帶來了解決科研生產的新思路。文獻[4-5]提供了仿生學應用于機械動力學的方法和思路,仿生學主要運用類比、模擬和模型方法,在理解生物系統工作原理的基礎上以實現其特定功能。
自然界中存在一種寄生蠅,能夠精確地定位寄主蟋蟀以繁衍后代。寄主蟋蟀叫聲頻率成分單一,約為4.8 kHz,波長約7 cm[6]。奧米亞棕蠅兩側耳蝸距離大約為450~520 μm,整個聽覺結構跨度僅為1.2 mm,約為聲源頻率波長的0.017倍[7]。陣列間距與聲源波長幾何尺度嚴重失配,但是寄生蠅能夠在極短時間(約500 ms)內準確探測蟋蟀位置,比人類快1 000倍,不論聲源在何方,都能調整身體方向以正對蟋蟀,甚至能察覺到2°的變化[8],這種卓越的聲源定位功能得益于聽覺結構的耦合放大機制。考慮將生物的優異特性應用于工程實踐中,那么首先需要研究它的運動機理。在前人建立的生物聽覺結構的簡化模型基礎上,文獻[9-10]研究了其物理本質并與工程實踐結合,達到超短基線測向的目的。
本文將仿生學耦合處理進行量化,結合旋轉干涉儀體制,既完成了測向解模糊,可以同時獲得高測向精度和寬測角范圍。通過對旋轉中陣列采樣,相當于利用兩根天線積累了多元均勻圓陣上的多組數據,提高了陣元利用率,突破了傳統陣列間距限制和天線數量限制,獲得較高精度和分辨率。
1 簡化力學模型分析
生物模型是基礎,技術模型是研究的目的,數學模型是二者之間的橋梁。微分方程是系統最基本的數學模型,系統的微分方程可以通過反映具體系統內在運動規律的物理學原理來獲取。首先建立對技術系統具備有益因素的生物模型,將膜間橋等效成通過剛度k3和阻尼c3連接的2個硬桿,膜間橋兩側鼓膜的動態特性和周圍結構等效成剛度k1,k2和阻尼c1,c2。鼓膜、鼓膜間橋與鼓膜連接的表皮內突、球狀聽神經及聽覺器官考慮成2個集中質量m1,m2。考慮奧米亞棕蠅兩側耳對稱性[11],k1=k2=k,c1=c2=c,m1=m2=m,建立簡化力學模型如圖1所示。根據牛頓第二定律,建立力學方程式。用物理學基本定理建立系統的微分方程是微分方程建模法中最重要的一種方法。
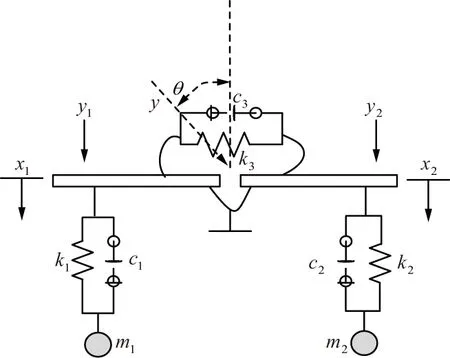
圖1 簡化力學模型
(1)
由簡化力學模型和公式初步推斷:模型的輸出取決于兩輸入的耦合作用,使得輸出響應與聲壓的入射方位等因素有關[12]。為了進一步揭示運動機理,求解其數學本質。
2 頻域分析
2.1 頻域響應
頻域響應是將時域響應進行傅里葉變換得到的,以頻率為變量的函數,也稱為譜函數。頻域振動響應更能揭示響應差異與耦合參數、入射角、陣列間距和聲音頻率的關系。對于粘性阻尼系統,可分為比例阻尼系統和一般阻尼系統。通常阻尼較小的結構可認為是比例阻尼系統,假設為比例阻尼系統[13]。
設Y(ω)是激勵信號y(t)的傅里葉變換,X(ω)是x(t)的傅里葉變換,對式(1)進行傅里葉變換,整理得:
(2)
式中,
D(w)=m(jw)2+j(c+c3)w+k+k3;
N(w)=jwc3+k3;
P(w)=D2(w)-N2(w)。
(3)
令Z1(w)表示兩激勵信號傅里葉變換的和,Z2(w)為兩傅里葉變換的差,有:
(4)
則:
(5)
將式(3)和式(5)代入式(2),整理得:
(6)
為得到頻域響應和振蕩頻率的直接關系,需要求出剛性系數、阻尼系數和振蕩頻率的關系。對于奧米亞棕蠅聽覺結構的運動力學方程,其自由度為2,所以1≤i≤2和1≤j≤2,設奧米亞棕蠅聽覺結構的模態陣型為:
(7)
則有:
(8)
(9)
由結構力學理論得到一階、二階模態的自由振蕩頻率(或稱為自然頻率)和阻尼比:
(10)
將式(10)代入式(6)得:
(11)
由式(11)可以看出,兩側響應是兩部分響應的疊加,機械耦合使得一側鼓膜不僅受到外部聲壓的作用,還受到另一側振動響應的影響,使得與聲壓同側的振動增強,另一側減弱,其結果是響應差異與聲壓有關,那么就可以根據差異與聲源的函數關系實現聲源定位。
2.2 響應幅度差和相位差
由聲壓信號y1=y(t+τ/2)和y2=y(t-τ/2),根據歐拉公式和傅里葉變換可得:
Y1(w)=Y(w)[cos(wt/2)+jsin(wt/2)],
Y2(w)=Y(w)[cos(wt/2)-jsin(wt/2)]。
(12)
則式(4)可寫為:
Z1(w)=2Y(w)cos(wt/2),
Z2(w)=2jY(w)sin(wt/2)。
(13)
式(11)可以寫為:
(14)
令:
(15)
則式(14)可以變成:
X1(w)=R2(w)+R1(w),
X2(w)=R2(w)-R1(w)。
(16)
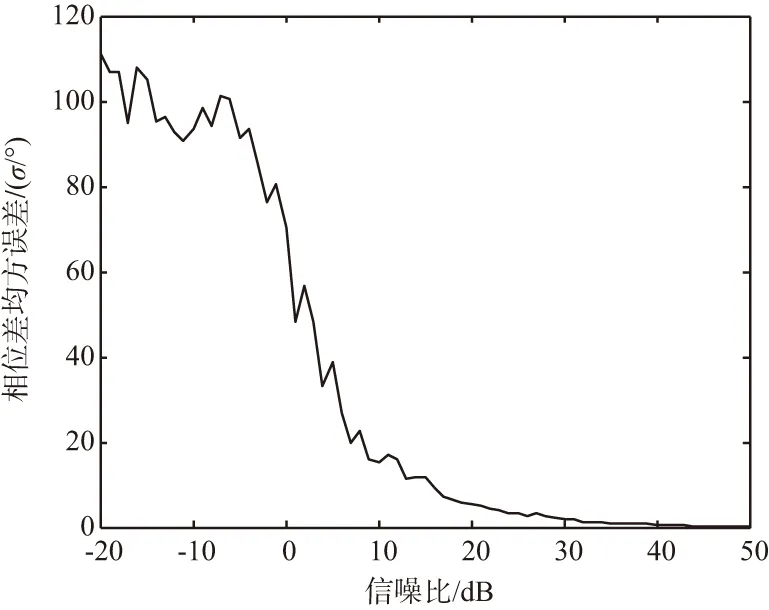
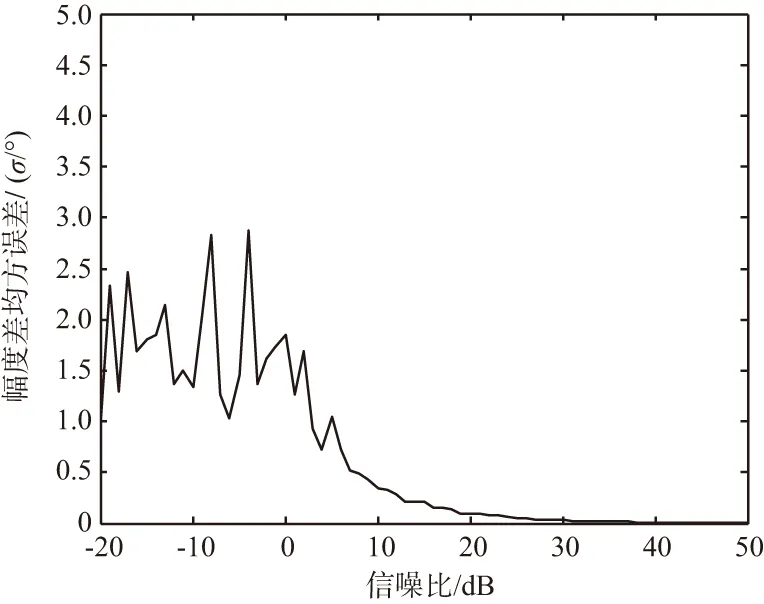
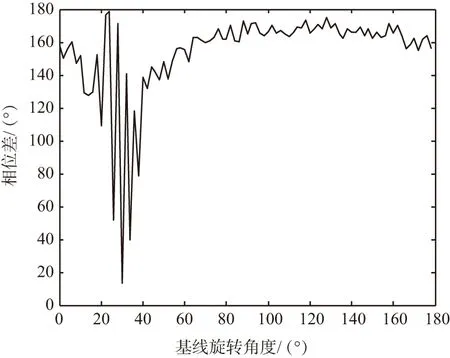
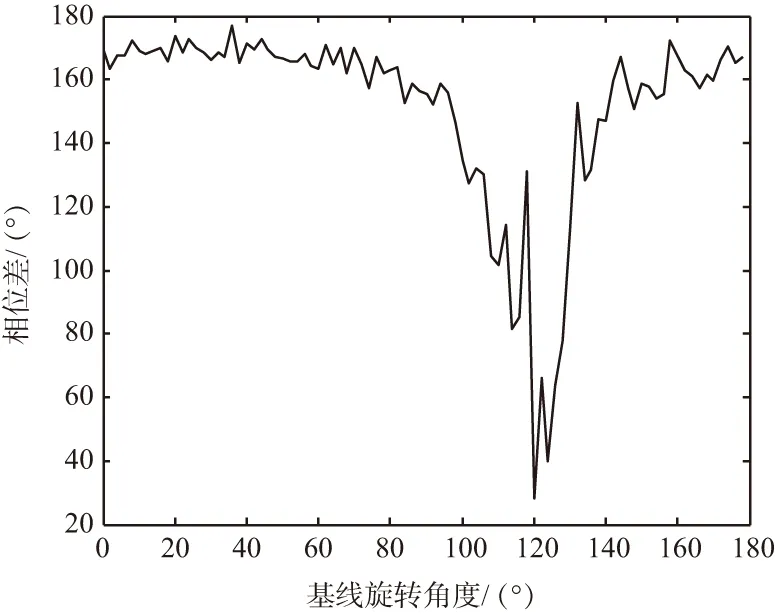
式(16)的響應合成可由圖2表示,設R1(w)和R2(w)的相位差分別是φ1和φ2,φ12=φ1-φ2表示R1(w)和R2(w)的相位差,φ0是兩側響應Y1(w)和Y2(w)的相位差。當聽覺結構不存在相互耦合,k3=c3=0,此時w1=w2,wt絕對值極小,所以|R2(w)|>>|R1(w)|,φ12為90°,此時不存在幅度差,但有較小的相位差。當存在耦合連接,w1 圖2 響應合成 根據勾股定理,可求得兩側響應幅度: (17) 將其展開整理得: (18) 幅度比為: (19) 幅度比取對數,以dB為單位的響應幅值差: (20) 式中, (21) cos(φ12)=cos(φ1-φ2)=cosφ1cosφ2+sinφ1sinφ2= (22) 式中,η1=w1/w,η2=w2/w。 根據圖2可得兩側響應相位差: (23) 將機械耦合處理機制與旋轉基線相結合,達到增強有效基線長度[14]的目的,首先仿真高斯噪聲對耦合處理機制的影響。 輸入振幅是1、頻率為5 kHz的單頻正弦波,設置參數為標準耦合參數,且聲源以45°入射,信噪比設置為-20~50 dB之間,仿真分析相位差和幅度差均方誤差隨信噪比的變化[10],如圖3和圖4所示。 圖3 相位差均方誤差隨信噪比的變化 圖4 幅度差均方誤差隨信噪比的變化 仿真結果可以看到,仿生耦合處理相位差響應和幅度差響應精度在20 dB時逐漸趨于穩定。那么設定信噪比為20 dB,與基線旋轉結合,測試定位效果。根據標準耦合參數優化參數設置如表1所示。 表1 耦合參數 參數值m/kg8×10-18k/(N·m-1)0.567k3/(N·m-1)5.18c/(N·s·m-1)1.92×10-9c3/(N·s·m-1)4.8×10-9 按表1設置耦合參數,信號頻率為30 MHz,波長λ=10 m,信號帶寬為0.6 MHz,載頻為300 MHz,采樣頻率為300 MHz,采樣間隔為1/300 MHz,樣本數1 024,角度饒基線旋轉自0°~180°,角度步長為1°,2PSK調制,陣元間距為d=0.1,λ=1 m,信噪比為20 dB,不同入射角下基線旋轉角度曲線如圖5~圖7所示。由仿真結果得到,結合耦合處理,旋轉基線測向與入射角度無關,在信噪比20 dB,陣列間距為信號波長的1/10情況下,仍能實現對信號源的有效測向,測向精度為2.110 5°。換言之,仿生耦合處理與傳統測向相結合,增加了有效基線長度。 圖5 信噪比為20 dB入射角為30°情況下的相位差響應 圖6 信噪比為20 dB入射角為60°情況下的相位差響應 圖7 信噪比為20 dB入射角為120°情況下的相位差響應 測向設備小型化是未來信息戰的發展趨勢,傳統測向理論認為,兼顧設備小型化與測向高精度是難以調和的矛盾[15]。本文研究了奧米亞棕蠅聲源定位機理,揭示了耦合參數和傳感器間距變化對耦合幅度差和相位差的影響及其函數關系。仿真驗證了高斯噪聲對實驗的影響,確定了噪聲門限,并與基線旋轉相結合,將陣列間距設置為0.1λ,即幾何尺寸嚴重不匹配的仿真環境下,實現了小基礎測向陣列的高精度定位。上述研究只針對力學模型的理想狀態,理論上能證明,仿真也得到了驗證,但實際應用環境復雜,存在各種干擾,運用到實際生產中還需要多番實際試驗和驗證。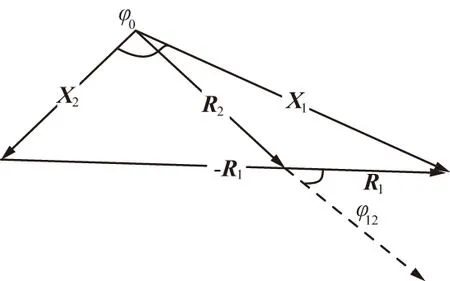
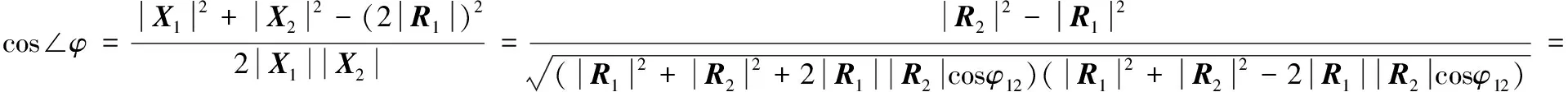
3 仿真分析


4 結束語

