基于干擾觀測器的球形移動機器人直線運動控制

于濤 王益博 孫漢旭 趙偉

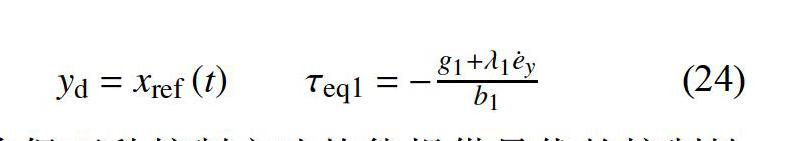
摘要：針對受擾球形移動機器人的直線運動控制問題，提出一種基于滑模干擾觀測器和雙冪次趨近律的分層滑模控制方法。該控制方法利用滑模干擾觀測器對未知擾動進行在線估計，并且采用基于滑模干擾觀測器的分層滑模控制器實現被控機器人系統的連續魯棒控制。首先設計被控系統的第一層和第二層滑動變量，然后基于第一層滑動變量定義系統的輔助滑動變量。基于所定義的輔助滑動變量設計滑模干擾觀測器，然后基于所設計的滑模干擾觀測器和第二層滑動變量，采用改進的雙冪次趨近律設計分層滑模控制器。從理論上分析所設計的分層滑模控制器作用下閉環系統的穩定性，并通過仿真實驗驗證所提控制方法的有效性。

關鍵詞：球形機器人;直線運動;分層滑模控制;干擾觀測器;雙冪次趨近律

中圖分類號：TP273 文獻標志碼：A 文章編號：1674-5124（2019）09-0123-07

收稿日期：2018-10-10;收到修改稿日期：2018-11-23

基金項目：遼寧省自然科學基金指導計劃項目（201602379）;遼寧省教育廳科學技術研究一般項目（L2015241）

作者簡介：于濤（1980-），男，天津市人，講師，博士，研究方向為機器人運動分析與控制、滑模控制理論與應用。

0 引言

隨著科技發展，移動機器人在不同的應用領域中發揮著日益重要的作用。球形移動機器人是一種具有球形外殼，并且通過滾動方式穿越地表環境的移動機器人。球形機器人移動時不需要借助任何可見的外部驅動，而且在工作空間中滾動時必須服從球——平面非完整約束。因此，球形移動機器人需要采用相對新穎的運動機構、巧妙復雜的動態分析方法和先進的控制算法[1-3]。球形外殼賦予球形移動機器人耐用、不會傾倒、與外界環境完全隔離的優點，在巡邏監視[4]、外星探測[5]、環境監測[6]、水下作業[7]，甚至兒童教育[8]等方面球形移動機器人都有著廣泛的應用。

球形移動機器人在工作空間內的滾動模式可以分為二維平面滾動模式和三維空間滾動模式。在二維平面滾動模式下，球形移動機器人進行典型的直線運動。從球形移動機器人直線運動控制方法的研究現狀[9-14]來看，大部分現有方法[9-13]采用被控對象的標稱模型[9-11]或標稱模型的線性化模型[12-13]來設計控制器;但由于實際對象中不可避免地存在著很多無法用數學模型精確描述的不確定性，并且在設計控制系統時忽略了這些不確定性對控制性能的不良影響，導致基于上述方法[9-13]的控制器在實際中很難實現預期的性能品質。由此可知，球形移動機器人直線運動的魯棒控制問題是目前該領域中亟待解決的重要問題之一。

針對球形移動機器人直線運動的魯棒控制問題，本文設計一種基于滑模干擾觀測器和雙冪次趨近律的分層滑模控制器。具體而言，首先基于第一層滑動變量設計球殼和單擺子系統的滑模干擾觀測器，然后提出一種改進的雙冪次趨近律以使第二層滑動變量快速收斂于零，最后基于改進的雙冪次趨近律和滑模干擾觀測器設計連續的分層滑模控制器。并通過理論分析與仿真實驗驗證本文所設計的分層滑模控制器確保閉環控制系統的魯棒穩定性。I球形機器人直線運動的動力學模型

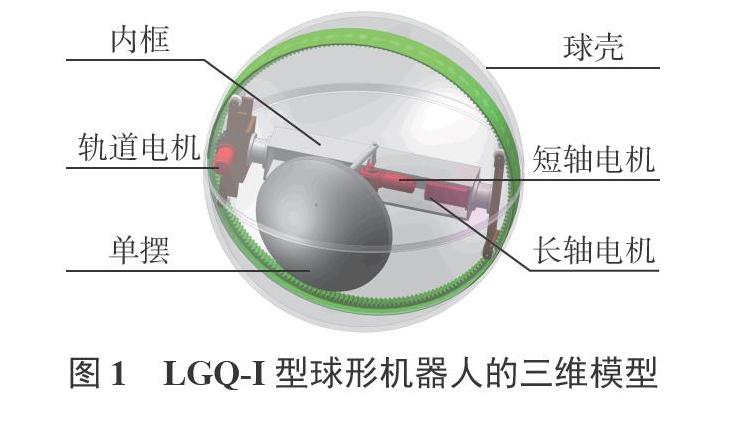
LGQ-I型三驅動球形機器人的三維模型如圖1所示，其本體結構主要包括球殼、內框、單擺和直流電機。與BYQ-XII型三驅動球形機器人[14]相比，LGQ-I型三驅動球形機器人內框的尺寸和質量較小，而單擺的質量和擺桿的長度較大。因此，LGQ-I型三驅動球形機器人的單擺質量相對總體質量的占比很高，因而能夠提供較大的偏心力矩，可以實現更迅速、更靈活的滾動運動。

當球殼內的長軸電機帶動內框和單擺相對球殼轉動時，球形機器人能夠進行向前或向后的直線滾動。當軌道電機帶動內框和單擺相對球殼轉動時，球形機器人能夠完成原地轉向動作。當短軸電機帶動單擺相對內框轉動時，球形機器人能夠在進行滾動運動時向左或向右轉向。由此可見，LGQ-I型三驅動球形機器人具有一定的容錯能力。當短軸電機或軌道電機出現故障時，球形機器人仍能實現全方位的滾動運動。

LGQ-I型三驅動球形機器人直線運動的簡化模型如圖2所示，在長軸電機輸出力矩：的作用下，球形機器人在XOZ平面內滾動。其中，球殼的質量為m₁，內框的質量為m₂，單擺的質量為m₃，球殼的半徑為r，單擺的擺桿長度為l，內框的轉動慣量為I，球殼的滾動角度為θ，球心的水平位移為x，單擺的擺動角度為φ。

基于拉格朗日法建立球形移動機器人直線運動的動力學模型，球形機器人系統的動能U為其中M=m₁+m₂+m₃，J=m₃l²+I。

球形機器人系統的勢能V為

V=-m₃9lcosφ（2）

利用含耗散函數的拉格朗日方程，由式（1）和式（2）可得球形移動機器人直線運動的運動方程為其中μ為粘滯摩擦系數;g為重力加速度。

假設球殼在地面滾動時不打滑，則有如下關系式成立：

θ=x/r θ=x/r（4）

將式砰）代入式（3），可得球形移動機器人直線運動的動力學模型為

M（q）q+N（q，q）=Fτ（5）

式中：

由動力學模型式（5），可得直線運動時球形機器人系統的非完整約束條件為

式中：

將球形移動機器人直線運動的動力學模型式（5）表示成如下形式：式中d₁（t）和d₂（t）表示包含外部干擾和模型不確定性的未知擾動。不失一般性，假設未知擾動dl₁t）和d₂（t）有界，即存在正常數L₁和L₂，使得|d₁（t）|≤L₁，|d₂（t）|≤L₂;f₁（x，φ，φ），f₂（x，φ，φ），b₁（φ），b₂（φ）的表達式分別為

2 基于干擾觀測器的分層滑模控制

2.1 問題描述

對于球形移動機器人，其直線運動的控制目標是：通過合理地設計控制律τ（t），使球心位置x（t）和單擺擺角φ（t）分別收斂至各自的期望值x_ref（t）和φ_ref（t）。不失一般性，假設球心和單擺擺角的期望軌跡x_ref（t）和φ_ref（t）關于時間t二階可導。根據被控機器人系統的控制目標，分別設計球殼子系統和單擺子系統的第一層滑動變量s₁（t）和s₂（t）為k2>0。

注1：由于球心的運動軌跡x（t）和單擺擺角的運動軌跡φ（t）滿足約束條件式（6），當給定球心的期望軌跡x_ref（t）時，可由式（6）相應地求得單擺擺角的期望軌跡φ_ref（t）。特別地，當球形移動機器人在地面上保持靜止或勻速前進時，即在球形移動機器人直線運動的位置控制問題或速度控制問題中，由式（6）可以推得單擺擺角的期望值為_ref=0。

由式（7）和式（8），進一步可得s₁（t）和s₂（t）為

s₁（t）=h₁+b₁τ+d₁s₂（t）=h₂+b₂τ+d₂（9）式中h₁=f₁+k₁ex-x_ref，h₂=f₂+k₂eφ-φ_ref。

基于所設計的第一層各滑動變量s₁（t）和s₂（t），進一步定義第二層滑動變量s₃（t）為

s₃（t）=c₁·s₁（t）+c₂·s₂（t）（10）式中c₁>0，c₂>0。

對式（10）求導并由式（9），可得s₃（t）為

s₃（t）=c₁s₁+c₂s₂=h₃+b₃τ+c₁d₁+c₂d₂（11）式中h₃=c₁h₁+c₂h₂，b₃=c₁b₁+c₂b₂。

至此，球形移動機器人直線運動的控制目標轉化為：在被控機器人系統式（7）存在未知擾動d₁（t）和d₂（t）的條件下，通過合理地設計控制τ（t）使式（11）所示的第二層滑動變量s₃（t）→0。

2.2 滑模干擾觀測器設計

首先采用滑模干擾觀測器對未知擾動dl（t）和d₂（t）進行在線估計，然后在此基礎上采用雙冪次趨近律設計分層滑模控制器以確保滑動變量s₃（t）快速趨近于零。

定義輔助滑動變量σ₁（t）和σ₂（t）為

σ_i（t）=s_i（t）+z_i（t），z_i（t）=-h_i-b_iτ-u_i，i=1，2

（12）式中z_i為滑模干擾觀測器i的內部變量，u_i為待設計的滑模干擾觀測器i的注入項。

由式（9）和式（12），可以得到

σ_i（t）=s_i+z_i=d_i-u_i（13）

基于式（13）所示的輔助滑動變量σ_i（t）的動態方程，設計滑模干擾觀測器i的注入項u_i（t）為

u_i（t）=ε_isign（σ_i），ε_i=L_i+ρ_i（14）式中ρ_i>0。很容易證明[15]，采用式（14）所示的滑模干擾觀測器注入項u_i（t），輔助滑動變量σ_i（t）能夠在有限時間t_ri≤|σ_i（0）|/ρ_i內收斂于零。

設滑模干擾觀測器i的注入項u_i（t）的等效控制為u_eq，i（t）。由等效控制原理和式（13）可知：在輔助滑動面σ_i（t）=0上，等效控制u_eq，i（t）能夠準確估計未知擾動d_i（t），即u_eq，i（t）=d_i（t），■t≥t_r，i。

實際中，采用干擾觀測器注入項u_i（t）的一階低通濾波平均值來計算其等效控制u_eq，i（t），即

γ_iu_eq，i（t）+u_eq，i（t）=u_i（t）（15）式中γ_i>0。

在式（15）中，選取很小的濾波時間常數γ_i，可使實際等效控制u_eq，i（t）足夠準確地逼近理想等效控制u_eq，i（t）a因此滑模干擾觀測器t可以通過式（15）所示的注入項等效控制u_eq，i（t）對未知擾動d_i（t）進行準確估計，即：

u_eq，i（t）=d_i（t），■t≥t_r，i（16）

2.3 分層滑模控制器設計

記t_r3=max（t_r1，t_r2）。由式（11）和式（16），可以得到：

s₃（t）=h₃+b₃τ+c₁u_eq1+c₂h_eq2，■t≥t_r3（17）

為使第二層滑動變量s₃（t）快速收斂于零，本文提出一種改進的雙冪次趨近律，然后基于改進的雙冪次趨近律設計分層滑模控制器。

基于文獻[16]提出的雙冪次趨近律，設計改進的雙冪次趨近律為式中λ₁>0，λ₂>0，λ₃>0，α>1，0<β<1。

注2：在改進的雙冪次趨近律式（18）中，前2項為冪次趨近項，第3項為指數趨近項。如果不考慮控制增益A_i的影響，當系統狀態遠離滑動面S3=0（即|s₃|>1）時，第1項起主導作用;當系統狀態接近滑動面S3=0（即|s₃|<1）時，第2項起主導作用;在系統狀態的趨近過程中，第3項的作用始終介于第1項和第2項之間。由此可見，改進后的雙冪次趨近律具有更快的趨近速度。由s₃=|s₃|sign（s₃）可見，指數趨近項-λ₃s₃實際上是冪指數為1的冪次趨近項。由此可知，改進的雙冪次趨近律式（18）實際上是一種特殊的三冪次趨近律。

由式（17）和式（1g），可得分層滑模控制器為

2.4 穩定性分析

分析1;對于式（7）所示的球形機器人系統，按式（8）和式（10）設計各層滑動變量，并按式（12）和式（14）設計滑模干擾觀測器，如果采用式（19）所示的分層滑模控制器，那么第二層滑動變量s₃（t）及其導數s₃（t）能夠在有限時間內收斂于零。

證明：將控制律式（19）代入式（11），可以得到

為便于分析，將第二層滑動變量s₃（t）的收斂過程分為兩個階段。第1階段為輔助滑動變量σ_i（t）的收斂階段（0r3

分析2：對于式（7）所示的球形機器人系統，按式（8）和式（10）設計各層滑動變量，并按式（12）和式（14）設計滑模干擾觀測器，如果采用式（19）所示的分層滑模控制器，那么第一層滑動變量s₁（t）和s₂（t）漸近收斂于零。

對于按式（8）設計的第一層各滑動變量，由文獻[18]定理4.2的證明可知，在分層滑模控制器式（19）的作用下，滑動變量s₁（t）和s₂（t）漸近收斂于零，即

3 仿真驗證

為驗證本文提出的控制方法的有效性，利用Matlab/Simulmk仿真環境進行球形移動機器人直線運動的速度控制實驗。LGQ-1型三驅動球形機器人的各參數分別為：m₁=1.45 kg，m₂=0.65kg，m₃=3.5kg，r=0.15m，1=7.63×10^-4kg·m²，l=0.107m，μ=0.02N·m/（rad/s）。

設球形移動機器人的初始狀態為：x（0）=0，x（0）=0，φ（0）=0，φ（0）=0。設球形移動機器人的期望速度為x_ref=1m/s，相應地選取球心的期望軌跡為x_ref（t）=t，單擺擺角的期望值為φ_ref=0。仿真實驗中，重力加速度取為g=9.81m/s²，長軸電機的最大輸出力矩設為|τ|_max=3.7N·m。設仿真時間為T=6s，采樣時間為t_s=0.001s。

為檢驗本文提出的控制方法的控制性能和魯棒性，假設實際球形機器人帶有10%的參數不確定性，在此基礎上與文獻[14]提出的控制方法進行對比分析。將文獻[14]提出的控制方法應用于直線運動的速度控制問題時，需要將球形移動機器人的期望軌跡y_d和滑動面s₁的等效控制τ_eq1相應地修改為

為確保兩種控制方法均能提供最優的控制性能，對基于兩種控制方法的控制器各參數進行充分整定。在進行仿真對比時，基于本文方法的控制器各參數分別為：k₁=0.64，k₂=5.9，c₁=7.1，c₂=2.6，ε₁=6.5，ε₂=28，λ₁=7.4，λ₂=9.2，λ₃=9.4，α=1.5，β=0.5。基于文獻[14]方法的控制器各參數分別為：λ₁=1.1，λ₂=7.5，α₁=7.1，α₂=1.6，ω（0）=2.3，σ=0.4，φ=0.1，k=8.3。

基于本文方法的控制器的控制效果如圖3至圖5所示。圖3為球心速度、單擺擺角和長軸電機輸出力矩的變化曲線，可見在基于本文方法的連續分層滑模控制器式（19）作用下，球心速度和單擺擺角分別于3.122s和3.039s收斂至各自的期望值。仿真實驗結果表明，本文方法能夠有效實現球形移動機器人直線運動的連續魯棒控制。圖4和圖5分別為各輔助滑動變量和各層滑動變量的變化曲線，可見各滑動變量均能快速地收斂于零。具體而言，由圖4可見輔助滑動變量的整體收斂時間為t_r3=0.149s，進而由式（22）可知第二層滑動變量的收斂時間估計為t_r4<0.637s;又圖5可見第二層滑動變量的實際收斂時間為t_r4=0.622s。由此可知，第二層滑動變量的實際收斂時間t_r4與式（23）所示的估算結果是相符的。

基于文獻[14]方法的控制器的控制效果如圖6所示。可以看出，在基于文獻[14]方法的控制器作用下，球心速度和單擺擺角分別于3.48s和2.891s收斂至各自的期望值。需要指出的是，雖然兩種控制方法均能實現被控球形機器人系統的連續魯棒控制，但本文方法采用的是連續的控制律，而文獻[14]方法采用的是連續化的控制律，這也是兩種控制方法的重要區別之一。此外，由仿真實驗結果可見：當球心速度趨于穩定后，長軸電機仍需提供一定的平衡力矩以補償內框與球殼之間的粘滯摩擦力。由動力學模型式（5）可以推得，長軸電機輸出的平衡力矩為τ_SS=μx_ref/r。考慮到參數不確定性的影響，由上式可以求得長軸電機實際輸出的平衡力矩為τ_SS=0.133N·m，所得結果與仿真實驗結果是一致的。

為評價球形機器人速度控制器的控制性能，分別定義球心速度平均跟蹤誤差E（x）和單擺擺角平均跟蹤誤差E（φ）為式中n為采樣點個數，t_i為第i個采樣時間點。

由式（25）可以分別求得在基于本文方法的控制器作用下和基于文獻[14]方法的控制器作用下，球心速度平均跟蹤誤差E（x）和單擺擺角平均跟蹤誤差E（φ）。以上兩種控制器作用下，各性能指標的計算結果如表1所示。

由表可以看出，相較于基于文獻[14]方法的控制器，在基于本文方法的控制器作用下，球心速度平均跟蹤誤差E（t）和單擺擺角平均跟蹤誤差E（φ）均較小。性能指標E（x）和E（φ）的對比結果表明，基于本文方法的控制器具有較好的控制性能。

4 結束語

本文探討了帶有未知擾動的球形移動機器人的直線運動控制問題，提出一種基于滑模干擾觀測器和改進的雙冪次趨近律的分層滑模控制方法。本文提出的控制方法利用干擾觀測器注入項的等效控制對被控機器人系統的未知擾動進行在線估計，并且采用基于干擾觀測器注入項的等效控制和改進的雙冪次趨近律的連續分層滑模控制器實現被控機器人系統的快速穩定。從理論上證明了各輔助滑動變量和各層滑動變量的收斂性，仿真實驗結果表明本文設計的分層滑模控制器能夠提供良好的控制性能和魯棒性。

參考文獻

[1]ARMOUR R H，VINCENT J F V.Rolling in nature androbotics：a review[J].Journal of Bionic Engineering，2006，3（4）：195-208.

[2]CROSSLEY V A.A literature review of the design ofspherical rolling robots[R].Pittsburgh，Camegie MellonUniversity，2006.

[3]CHASE D，PANDYA A.A review of active mechanicaldriving principles of spherical robots[J].Robotics，2012，1（1）：3-23.

[4]WU F，VIBHUTE A，SOH G S，et al.A compact magneticfield-based obstacle detection and avoidance system forminiature spherical robots[J].Sensors，2017，17（6）：1-20.

[5]HOGAN F R，FORBES J R，BARFOOT T D.Rolling stabilityof a power-generating tumbleweed rover[J].Journal ofSpacecraft and Rockets，2015，51（6）：1895-1906.

[6]HERNANDEZ J D，BARRIENTOS J，CERRO J D，et al.Moisture measurement in crops using spherical robots[J].Industrial Robot：An International Journal，2013，40（1）：59-66.

[7]LI Y，YANG M，SUN H，et al.A novel amphibious sphericalrobot equipped with flywheel，pendulum，and propeller[J].Journal of Intelligent and Robotic Systems，2017，2：1-17.

[8]MICHAUD F，LAPLANTE J F，LAROUCHE H，et al.Autonomous spherical mobile robot for child-developmentstudies[J].IEEE Transactions on Systems，Man，andCybernetics，2005，35（4）：1-10.

[9]MADHUSHANI T W U，MAITHRIPALA D H S，BERG J M.Feedback regularization and geometric PHD control fortrajectory tracking of mechanical systems：hoop robots on aninclined plane[C]//American Control Conference，2017.

[10]ZHAN Q，CHI X，XI X.Linear motion control of anunderactuated spherical mobile robot[J].Applied Mechanicsand Materials，2014，644-650：351-355.

[11]IVANOVA T B，PIVOVAROVA E N.Dynamics and controlof a spherical robot with an axisymmetric pendulumactuator[J].Physics，2015，9（3）：507-520.

[12]YE P，SUN H，QIU Z，et al.Design and motion control of aspherical robot with stereovision[C]//IEEE Conference onIndustrial Electronics and Applications，2016.

[13]YUE M，LIU B.Disturbance adaptive control for anunderactuated spherical robot based on hierarchical sliding-mode technology[C]//Chinese Control Conference，2012.

[14]于濤，孫漢旭，趙偉，等.基于自適應分級滑模控制的球形機器人定位控制[J].中國測試，2018，44（5）：97-102.

[15]UTKIN V，GULDNER J，SHI J M.Sliding mode control inelectro-mechanical systems[M].Boca Raton：CRC，2009：216.

[16]梅紅，王勇.快速收斂的機器人滑模變結構控制[J].信息與控制，2009，38（5）：552-557.

[17]張合新，范金鎖，孟飛，等.一種新型滑模控制雙冪次趨近律[J].控制與決策，2013，28（2）：289-293.

[18]QIAN D，YI J.Hierarchical sliding mode control for under-actuated cranes：design，analysis and simulation[M].Berlin：Springer-Verlag，2016：83.

（編輯：莫婕）