基于三重修正的WSN節點定位方法

王 梟,劉瑞敏,毛劍琳

(昆明理工大學 信息工程與自動化學院,昆明 650500)

無線傳感器網絡是一種被部署在受控區域的多跳自組織網絡,它由大量的具有通信與感知能力的傳感器節點構成,在入侵檢測、工業自動化、智能建筑等眾多領域有著極其廣泛的應用[1-4]。在任何領域中，只要涉及到無線傳感器網絡的應用,那么它的節點定位就起著不可估量的作用。目前,在節點定位技術中,主要有基于測距和基于非測距的定位技術。雖然基于測距的定位技術通過節點間的絕對距離來計算節點的位置,精度相對較高,但是，在大型區域中它會產生較高的硬件成本,同時也會產生較高的能耗。然而，基于非測距的定位技術僅需要節點間的互連來實現定位,因需要較少的硬件支持,成本比較低廉而受到青睞[5]。在測距定位中,研究較為廣泛的是TOA，TDOA，RSSI，AOA等技術;在非測距定位中,對于Centroid，APIT，DV-HOP技術的研究較為廣泛。

本文在DV-HOP算法的基礎上進行改進優化，使得定位效果更佳。DV-HOP技術通過錨節點與未知節點間的相互通信來獲取每個未知節點到錨節點的最小跳數值,然后，根據錨節點間的跳數與距離,計算出錨節點的平均跳距,最后，未知節點通過跳距計算出到錨節點距離,再根據某種計算方法計算出未知節點的坐標。DV-HOP算法由于其在實際環境定位中無需測距設備,可以大大降低網絡的成本,因此，在實際應用中具有獨特的優勢。當DV-HOP在大規模網絡中被應用時,它的關鍵問題是如何設計跳數機制、如何能有效降低跳距的誤差以及如何能較準確地求出未知節點的定位算法。實際上,由于網絡中未知節點的數量多于錨節點數的原因,利用錨節點的跳距來求錨節點與未知節點間的距離是造成距離誤差的一個因素;另外,由于錨節點間的跳數可能會存在不是整跳數的情況,按照傳統整數跳數機制就會使得跳距出現偏差;最后,在定位算法中由于沒有對未知節點與錨節點間的距離進行誤差校正而使得定位效果較差。但是由于DV-HOP定位精度較低的缺點,使得許多研究人員致力于定位精度優化算法的研究[6]。因此,國內外的研究學者們紛紛對DV-HOP算法做了不同的改進與優化。趙雁航等[7]首先對跳距進行修正,然后，通過粒子群優化算法來降低定位誤差;文獻[8]通過距離校正因子結合傳感器節點的通信半徑校正未知節點到信標節點的平均跳距;文獻[9]引入跳數因子,通過跳距的誤差加權來進行跳距的修正,最后，通過加權最小二乘來定位;文獻[10]中錨節點先將跳距傳播給鄰居的未知節點,然后，依據此跳距計算出錨節點間的估計距離，計算出與錨節點間實際距離的誤差,并且將此誤差的百分比作為權重來計算未知節點的跳距;文獻[11]依據最小均方誤差來求出每個錨節點的跳距,然后，將某個錨節點間跳數的倒數與所有錨節點間跳數的倒數之和的比作為加權值來對跳距進行加權,最后，采用雙曲線定位算法進行定位;徐慧娟等[12]利用相似度對測距值進行校正,然后，將最小二乘法得到的未知節點坐標作為遺傳模擬退火算法的初始解進行迭代，得到比較優良的未知節點坐標;劉登峰等[13]將定位問題轉換為優化問題,利用布谷鳥差分優化算法進行優化求解,可以有效地規避定位過程中誤差積累的缺點。雖然一直有許多研究學者在DV-HOP方面做出了大量的研究與改進,但是依舊有些問題是需要繼續研究的,包括未知節點到錨節點的跳距、符合實際情況的跳數機制、在定位算法中未知節點到錨節點的距離誤差校正等問題。

本文提出一種基于三重修正的無線傳感器網絡定位算法(triple correction localization algorithm),以下簡稱TC定位算法。在計跳階段,采用新的跳數計跳機制;在跳距階段,通過質心定位算法來對錨節點的跳距加權得出未知節點的跳距,減小節點的距離誤差;在定位階段,采用最小二乘法校正傳感器節點的距離矩陣。最后，通過高斯牛頓算法進行定位求解,有效地減小定位過程中產生的誤差。

1 定位模型

該算法模型共含有3個步驟:

step1估計所有節點跳數。錨節點以泛洪的方式將它自身的信息傳播到整個網絡中,這些信息分別包括坐標、id、跳數。直到網絡中的節點全部連通時,所有的未知節點即可獲取到錨節點的跳數。當多個錨節點給同一未知節點傳播坐標信息時,未知節點只保留跳數值最小的信息。這樣就得到了未知節點到所有錨節點的跳數信息。

step2估計錨節點的平均跳距。錨節點根據自己的坐標與到其他錨節點的跳數信息計算錨節點的平均跳距,然后，錨節點將本身的平均跳距傳播到網絡中。錨節點i到其他未知節點的平均跳距如式(1)所示，

(1)

其中：(xi,yi)，(xi,yj)分別表示錨節點i，j的坐標;N表示錨節點的個數；Hi,j表示錨節點i，j之間的跳數。根據已經得到的跳數信息與錨節點的平均跳距計算出未知節點z到錨節點i的距離，如式(2)所示，

Di,z=WHD_i×Hi,z。

(2)

其中：Hi,z表示錨節點i到未知節點z的跳數；Di,z表示錨節點i到到未知節點z的距離。

step3估計未知節點坐標。根據第2步中未知節點與錨節點的距離信息,利用定位算法估計未知節點的坐標。

2 TC定位算法

傳統DV-HOP算法在計跳階段以整數的形式對節點間的跳數來計量,但實際中的跳數并不都是整數,所以，在整個網絡中會造成誤差的積累;在錨節點的平均跳距階段,由于每個錨節點到所有未知節點的跳距相同,當未知節點較多時,也會出現誤差較大的情況;另外,由于跳數、跳距獲得過程中累積的誤差,在計算未知節點到錨節點間的距離時，勢必會產生較大偏差,所以，應該在定位階段加入校正未知節點到錨節點距離的環節。因此,文中首先利用新的跳數機制實現非整數的計跳,再通過質心算法對不同錨節點到每個未知節點的跳距進行加權，得出較合理的未知節點的跳距,然后，利用最小二乘法對未知節點到錨節點的距離矩陣進行校正,最后，根據校正后的距離矩陣，利用高斯牛頓算法來得出比較準確的未知節點位置。

2.1 新的跳數機制

按照傳統的計數方式,當節點在它的通信半徑內可以與其他節點通信時，就認為這些節點間的跳數為1跳,但這種辦法在實際應用中是不太合理的,所以，將跳數機制修正成式(3)，

(3)

其中，

(4)

(5)

ai=min(Dalli,j)。

(6)

其中：Dalli,j表示錨節點i，j的距離；Di表示其他錨節點到錨節點i的平均距離；ai表示與錨節點i距離最近的錨節點的距離值。

2.2 跳距修正

通過質心定位算法[14]對錨節點的跳距進行加權，作為未知節點的跳距。錨節點的跳距是在已經校正跳數的前提下按照式(1)計算得到。未知節點z的跳距如式(7)所示，

WHD_z=HOPT×Cent_Weigh。

(7)

其中：HOP是錨節點的跳距矩陣,是一個N行1列的矩陣;Cent_Weigh是一個N行1列的矩陣,這個矩陣中第i個元素為

Cent_Weigh(i)=

(8)

其中：(xi,yi)是錨節點的坐標；(xz,yz)是由質心算法計算出的未知節點的坐標；N表示錨節點的個數。

2.3 定位算法

未知節點的求解過程可以看作求解非線性方程組,而高斯牛頓法是求解非線性方程組的一種有效方法[15]。但是，直接利用高斯牛頓算法會由于錨節點與未知節點間的距離誤差而造成定位精度下降,所以，在采用高斯牛頓算法定位前，應對未知節點到錨節點的距離進行校正。

在經過計跳與跳距修正以后,可以得到未知節點z到錨節點i之間的距離，

Diz=WHD_z×Hi,z。

(9)

通過最小二乘法對式(9)的距離進行校正,

Derror＿iz=

(10)

其中：(xls_z,yls_z)表示由最小二乘法得到的第z個未知節點的坐標；Diz表示第i個錨節點到第z個未知節點的距離；Derror＿iz表示錨節點i與未知節點z的距離誤差。

經過校正后的未知節點z到錨節點i的距離為

Dcor＿iz=Diz+Derror＿iz。

(11)

其中,Dcor＿iz表示已經經過校正的未知節點z與錨節點i的距離。

假定Xz為未知節點,未知節點坐標為(xz,yz)。Bi為n個錨節點中的第i個錨節點,它的坐標為(xBi,yBi)。Diz表示未知節點Xz到錨節點i的距離, 是經過校正的,即Diz∈Dcor_z。未知節點z到錨節點的距離的方程組如式(12)所示，

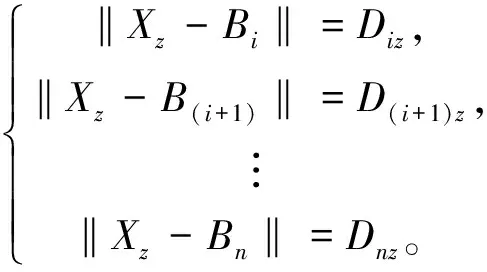
(12)

其中:‖·‖表示歐幾里得范數；n表示錨節點的個數。

經過前期的校正算法后,得到了比較高效的未知節點與錨節點之間的距離矩陣,最后，將問題轉化為求解式(13)中的非線性方程組,采用高斯牛頓算法進行求解。將未知節點求解的問題轉化最小二乘問題,如式(13)所示，

(13)

其中,dz如式(14)所示，

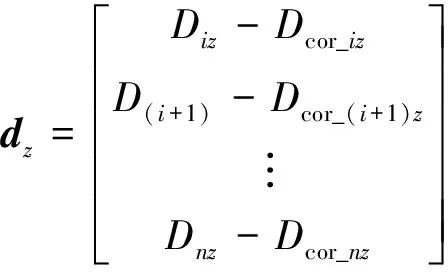
(14)

設Xk為經過k次迭代所得到的未知節點坐標,根據式(13)可以得到第k+1次的未知坐標，

X(k+1)=X(k)+λ×ΔX，

(15)

ΔX=-[JT(X)J(X)]-1J(X)e(X)，

(16)

e(X)=‖Xz-B‖-Dz。

(17)

其中,λ為迭代步長,需要根據實驗進行設置,式(16)中J為雅克比矩陣。

具體的TC定位算法步驟如下：

step1部署網絡,錨節點以泛洪方式在整個網絡中傳播自己的信息,并且根據式(3)，(7)，(9)來計算錨節點到位置節點的距離,再通過式(11)對未知節點到錨節點間的距離矩陣進行校正；

step2對未知節點z的位置X、迭代次數iter、迭代步長λ、迭代誤差ε和當前迭代次數k進行初始化；

step3計算式(16)的雅克比矩陣,根據式(14)進行迭代更新；

step4只要f(x)的值滿足迭代誤差,則將此時未知節點z的坐標輸出，否則，返回至step3繼續迭代,令k=k+1,直至達到迭代次數要求；

step5輸出位置節點的坐標。

3 仿真實驗與分析

為了驗證文中所提算法的性能,在Matlab上進行仿真實驗。文獻[9，11]中的定位算法是在DV-HOP的基礎上進行改進的，所以，本文與文獻[9，11]中的算法進行比較。另外,在本文修正跳距、跳數的基礎上,利用最小二乘法(LS)進行定位,并與本文所提算法進行對比。布置傳感器的檢測區域為100m×100m,隨機撒200個節點,傳感器的通信半徑為25m,錨節點的比例為s%,假定拋撒之后的傳感器節點不移動,并且錨節點的通信半徑都是相同的.每次實驗在相互獨立的條件下進行50次，取50次的平均誤差值作為定位誤差值。

將歸一化的定位誤差作為衡量定位性能的標準,如式(18)所示，

(18)

其中：(xtl,ytl)和(xl,yl)分別是傳感器節點的真實坐標和估計坐標；s為未知節點的個數；r為傳感器節點的通信半徑。

圖1給出了傳感總節點數與平均定位誤差的關系曲線。設置信標節點的比例為25%,通信半徑為25m。從圖1中可知,隨著傳感器節點數量的增加,本文所提算法的定位效果均優于其他3種定位算。

圖2為錨節點的通信半徑變化對定位誤差的影響。設置信標節點的比例為25%,傳感器總節點數為200。從圖2可以得知,隨著通信半徑的增加,在25m與35m之間,本文所提算法的定位誤差比其他3種定位誤差小。但是在35m之后,本文所提算法的精度開始有所下降,進而可以得知,在適當的通信半徑范圍之內,對未知節點與錨節點間的距離校正會起到正向作用,如果超出通信半徑范圍，由于距離校正起到反作用，從而導致定位精度反倒下降。多跳方式是引起距離測量誤差的一種因素，通信半徑變大到一定程度,即圖2中的35m,錨節點可以與更多的未知節點在通信半徑內進行通信,減少了需要多跳方式進行通信的未知節點,所以，加上跳數與跳距環節的修正,通信半徑較大的錨節點與未知節點間的距離測量誤差本來就很小了，在這個情況下加入距離校正,會導致圖2中過校正的情況。

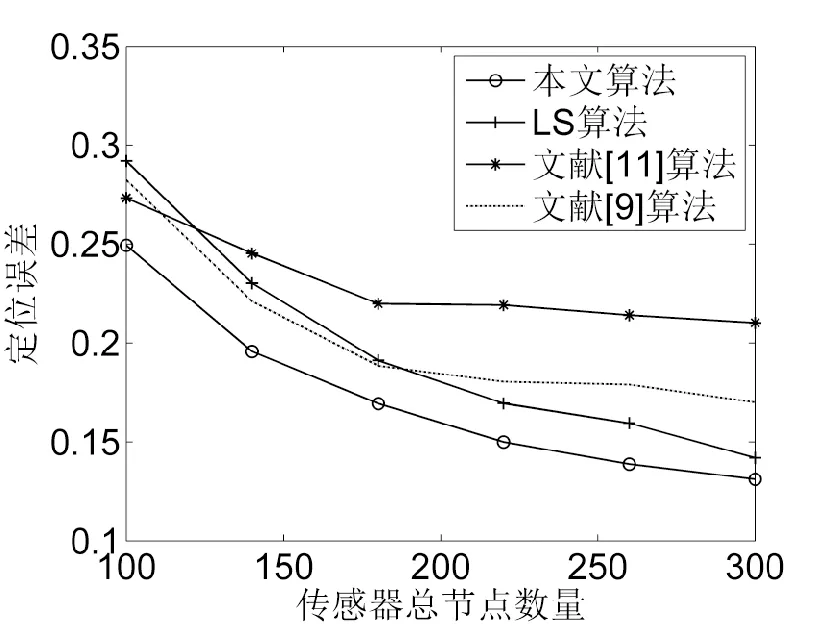
圖1 傳感器總節點數變化對定位誤差的影響Fig.1 The effect of the total number of sensors on the positioning error

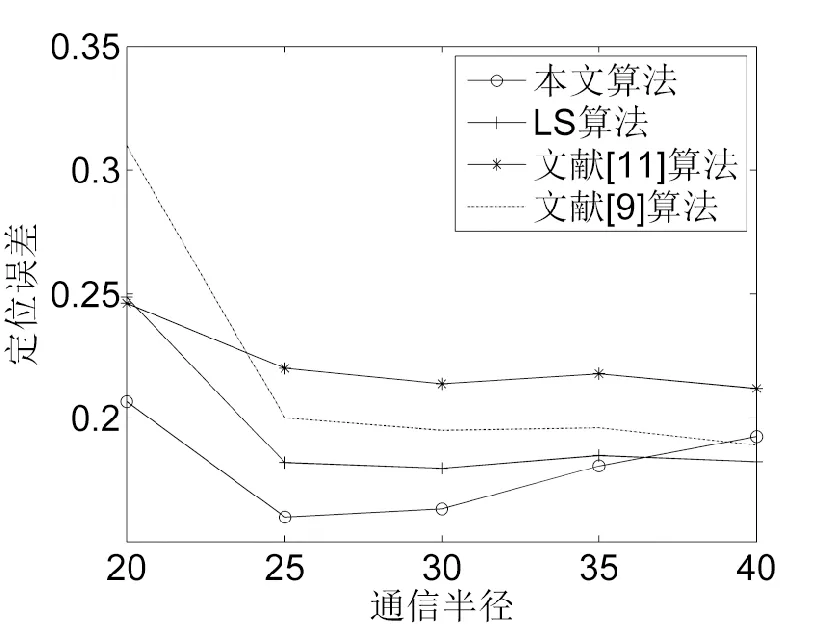
圖2 通信半徑變化對定位誤差的影響Fig.2 Effect of communication radius change on positioning error

圖3中給出了錨節點比例對定位誤差的影響曲線關系。設置傳感器總節點數為200,通信半徑為25m。從圖3中可以看出,隨著錨節點比例的增加,本文所提算法的誤差在不斷減小,由此可以得知所提算法的有效性。另外,在圖3中可以看到,本文所提算法的定位誤差均比其他3種算法的誤差小,可以得知，本文算法在定位中具有較好的優勢,能夠提高定位精度。

圖3 錨節點比例變化對定位誤差的影響Fig.3 Effect of anchor node ratio change on positioning error

4 結 語

為了有效應對傳感器網絡定位誤差較大的問題,本文提出一種基于三重修正的定位算法。首先，給出了新的計跳機制計算公式；然后，結合質心定位算法計算未知節點的跳距；再利用最小二乘法對未知節點與錨節點間的距離矩陣進行修正；最后，利用高斯牛頓法對未知節點與錨節點所組成的非線性方程組進行優化求解。另外,再通過Matlab實驗平臺進行仿真實驗,分析不同因素對定位誤差的影響。通過對比其他算法的定位效果,驗證了本文所提算法能夠有效提高定位精度。在下一步的研究中,可以與多位標度、模糊翻轉等技術結合，開發更加完備的無測距定位算法。