含時滯反饋控制的直齒圓柱齒輪主共振分析

石慧榮，趙冬艷，李宗剛，張軍平

(蘭州交通大學 機電工程學院，蘭州 730070)

直齒圓柱齒輪傳動以其結構緊湊、傳動準確、經濟性好等特點被廣泛應用于汽車、機床、船舶、航空等工業生產領域，其傳動性能決定了應用裝備的使用性能，因此對齒輪傳動的減振控制具有重要實際意義。然而由于齒輪傳動具有比較復雜非線性行為，所以應用中很難確定與之匹配的控制參數，因此控制參數對齒輪系統穩定性的影響已成為該領域的一個重要課題。

齒輪傳動系統非線性行為已經被廣泛研究，主要集中在側隙、時變嚙合剛度、載荷波動和制造裝配誤差等對傳動的影響上。Moradi等[1]利用多尺度法分析了含間隙的直齒圓柱齒輪系統的動力學特性，結果表明在特定參數下主共振、超諧波和亞諧波共振均會出現跳躍和不穩定現象。Lu等[2]利用數值計算法研究了影響直齒圓柱齒輪傳動非線性特性的因素，結果表明輕載時更容易導致系統出現混沌，系統參數的合理匹配能提升其傳動的穩定性。Singh[3]利用Floquet定理分析了考慮齒面摩擦作用的斜齒輪扭轉傳動特性，表明摩擦作用力對斜齒傳動影響較小。張微等[4]利用多尺度法分析了直齒圓柱齒輪傳動的穩定性，結果表明當輪齒嚙合頻率接近和型共振頻率時，系統會發生參數共振，存在著不收斂的無界解。魏莎等[5]運用區間諧波平衡法分析了考慮區間系統參數的齒輪副非線性系統動態響應，研究表明側隙、阻尼和載荷參數對系統動態特性具有較大影響。為了提升齒輪系統的傳動性能，一些主動減振方法也受到一些學者的關注。Chen等[6]提出一種改變嚙合剛度的齒輪傳動主動減振方法，并驗證了其有效性。Li等[7-8]提出了一種利用壓電堆裝置主動控制齒輪轉子支撐裝置振動從而抑制齒輪傳動振動的方法，并實驗驗證了控制方法的有效性。李以農等[9]對齒輪傳動壓電堆作動減振提出一種自適應算法主動控制方案，并對其進行了實驗驗證。

綜上所述，現有的研究主要關注傳動系統內部參數對系統非線性行為的影響或特定控制方法的減振作用，綜合考慮控制參數和齒輪系統參數的動力學行為研究還比較少。本文為了有效減小直齒圓柱齒輪系統由于外載荷激勵波動和時變嚙合剛度引起的振動，對系統施加時滯反饋控制，并采用多尺度法分析齒輪系統載荷波動和嚙合剛度波動對主共振的影響，研究時滯反饋控制參數對齒輪傳動動態特性的影響。

1 時滯反饋直齒圓柱齒輪傳動系統模型

齒輪傳動系統由于制造誤差、裝配誤差、側隙、時變嚙合剛度和齒面接觸變形等因素的影響，嚙合齒對間的作用力很難確定，因此齒輪系統的動態特性比較復雜，但本文主要研究嚙合剛度變化和外加激勵載荷對系統傳動的影響，因此可以將其簡化成一個單自由度系統[10]，假定軸承和軸的支撐剛度遠大于齒輪的嚙合剛度，此時可以近似認為齒輪與支座剛性連接，所以只考慮扭轉自由度，由此可得齒輪系統的動力學方程為

(1)

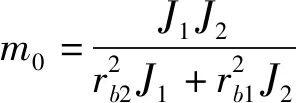
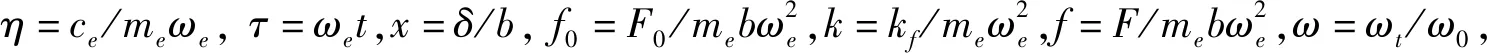
(2)

無量綱化的側隙函數為

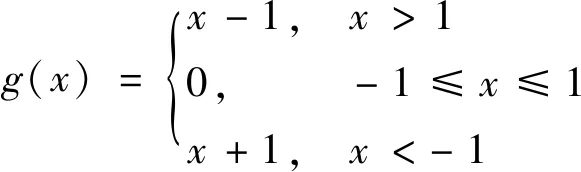
(3)

根據文獻[1]對齒輪傳動的研究方法，可以將側隙函數近似為

g(x)=d1x+d2x3=d1(x+d0x3)

(4)

其中d0=d2/d1，當d1=0.463，d2=0.016 04時，擬合均方差0.21，確定系數為0.989 8，此時式(4)的側隙函數能夠較精確地反映分段函數(3)所表示的輪齒接觸、脫齒和齒背沖擊現象，并且使系統光滑化。將式(4)代入式(1)中，齒輪系統轉變為一種類Mathieu-Duffing振子，并考慮對齒輪支撐系統施加時滯位移速度反饋控制，根據文獻[13]可以得到時滯反饋齒輪傳動系統的數學模型為

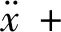
(5)

2 時滯反饋齒輪傳動系統的多尺度法分析

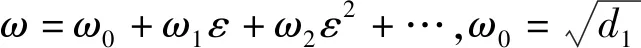
x(t)=x0(T0,T1,…)+εx1(T0,T1,…)+

ε2x2(T0,T1,…)+…

(6)

x(t-τ)=x0τ(T0,T1,…)+εx1τ(T0,T1,…)+

ε2x2τ(T0,T1,…)+…

(7)

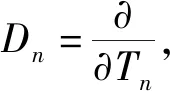
(8)

(9)

為了獲得有效的近似解，必須使嚙合阻尼、嚙合剛度波動量、非線性項、激勵載荷與控制增益為同階量，因此重新標定系統參量η=2εμ，k=εk，d0=εd0，f=εf，g1=εg1，g2=εg2，并將偏導算子(8)和(9)以及近似解(6)和(7)代入齒輪的系統方程(5)中，令ε0和ε1的系數相等可得

(10)

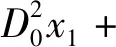
g2D0x0τv-2μD0x0-2D0D1x0-

(11)

Aτ(T1)=Aτ(T1-ετ)≈A(T1)-ετA(T1)+…

(12)

同時令cosωτ=(eiωτ+e-iωτ)/2，將x0和式(12)代入式(11)可得

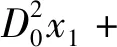
d2A2[Ae3iω0T0+3f0e2iω0T0]+

(13)

式中，cc表示前面各項的共軛。式(13)可能存在的多種諧波響應分別為

(1)微共振：ω≈0；

(2)主共振：ω≈ω0；

(3)次諧波共振：ω≈2ω0。

3 時滯反饋齒輪系統的主共振穩定性分析

本文主要對齒輪傳動系統的主共振特性進行分析，引入激勵頻率失調參數σ，使得

ω=ω0+εσ

(14)

為了消去永年項，令上式中含有eiω0T0的系數為零，可以得到

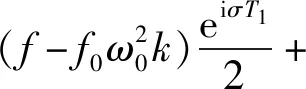
iω0A(g2e-iω0τv-2μ)

(15)

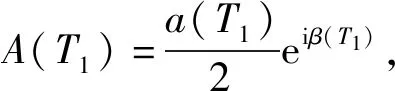
(16)

(17)

其中

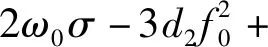
(g2ω0sinω0τv+g1cosω0τd)

N=(2ω0μ-ω0g2cosω0τv+g1sinω0τd)

(18)

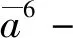
(19)

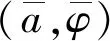
(20)

因此矩陣的特征值方程為

(21)

要使特征值λ具有負實部保證系統的穩定性，式(21)必須滿足以下條件

N>0

(22)

4 主共振的數值分析

針對簡化的齒輪傳動系統，初始傳動參數由表1給出，無量綱化后的靜載荷f0=0.215，載荷波動幅度f=0.2，嚙合剛度波動幅值k=0.2，嚙合阻尼μ=0.1，小參數ε=0.02，位移和速度反饋增益g1=g2=0.1，時滯為τd=τv=T/9，其中T=2π/ω0，后續分析中未作特定說明，各參數均為初始參數。為了更加全面了解齒輪傳動系統的動態特性，數值分析主要探討外加激勵波動、嚙合剛度波動、遲滯反饋參數對齒輪系統主共振的影響。

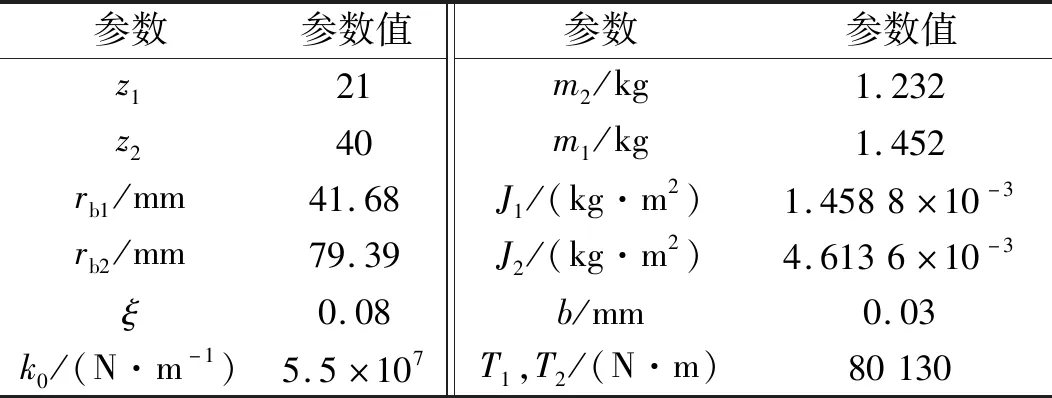
表1 齒輪參數表Tab.1 Gear parameters

4.1 載荷波動對傳動的影響

當g1=g2=0時無時滯反饋作用，此時載荷波動幅度f對主共振的影響如圖1所示，圖1(a)為不同外加載荷波動f時齒輪系統的幅頻變化關系，圖中灰色部分為不穩定振動分支，由圖可以看出，當外加激勵波動f逐漸增大時，主共振幅值增大，灰色不穩定分支增加，系統的定性變差，在較大的f作用下才會引起振幅的“跳躍”。圖1(b)表明當激勵頻率ω小于齒輪系統的主共振頻率時，振幅隨f的增大逐漸增大，在ω大于主共振頻率進入不穩定頻帶后出現多個振幅分支，從而引起系統的不穩定，這也稱之為滯后現象。因此在接近主共振的齒輪傳動系統中應注意控制嚙合齒對的載荷波動，保證傳動的穩定性和可靠性。

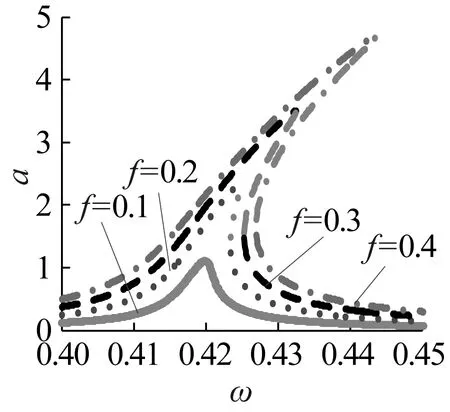
(a)

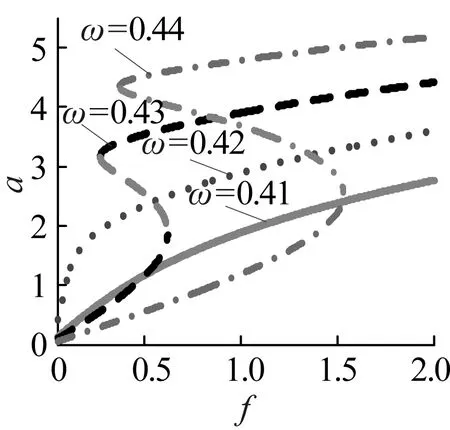
(b)圖1 載荷波動對振幅影響Fig.1 The effect of load fluctuation on the amplitude

4.2 嚙合剛度波動對傳動的影響

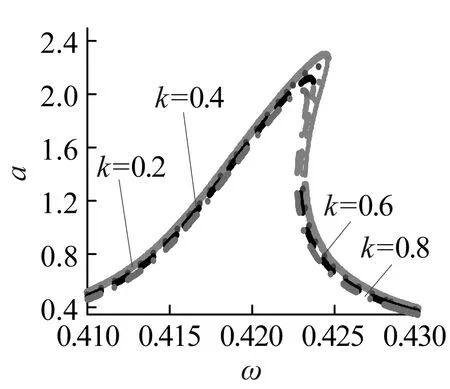
同樣在g1=g2=0時，嚙合剛度波動k對主共振影響如圖2所示，由圖2(a)可以看出，隨著嚙合剛度波動k的增加，主共振的最大穩態幅值逐漸減小，不穩定分支也不斷縮聚，因此一定嚙合剛度波動會縮減主共振穩態幅值，提高主共振的穩定性，但k對主共振穩態幅值的影響比較小。圖2(b)表明當激勵頻率ω進入不穩定區域后，k在一定范圍內變化會導致齒輪系統主共振的失穩，而且ω越大，觸發主共振不穩定的最小k越小，而且較小的k亦可誘發系統的大幅振動，導致主共振穩態幅值的多值性，引起主共振的不穩定。實際傳動中k越小，傳動的穩定性較好，但在接近主共振頻率時，雖然嚙合剛度波動幅度較小仍然可能引起系統的大幅振動。

(a)

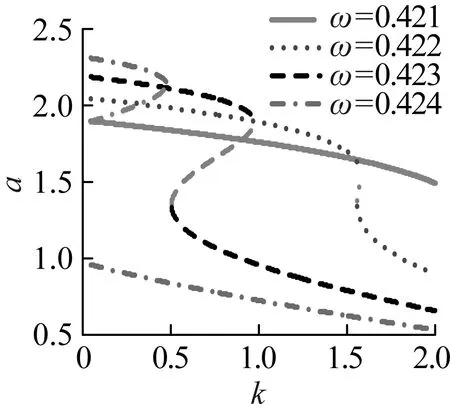
(b)圖2 嚙合剛度波動對振幅影響Fig.2 The effect of mesh stiffness on the amplitude

4.3 控制參數對傳動的影響

由于齒輪傳動系統的外加載荷波動和嚙合剛度波動會引起系統傳動的不穩定，因此為了減小系統振動，提升運轉穩定性，對其施加時滯反饋控制，特定控制參數變化時齒輪系統的主共振特性由圖3和圖4給出。

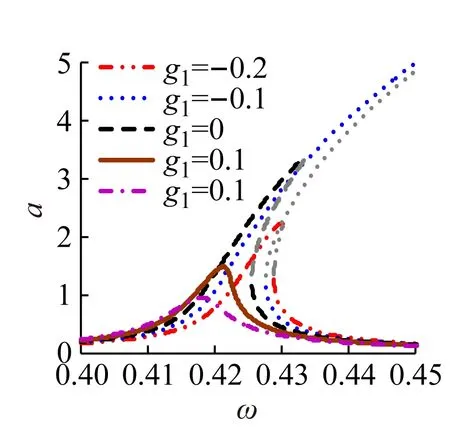
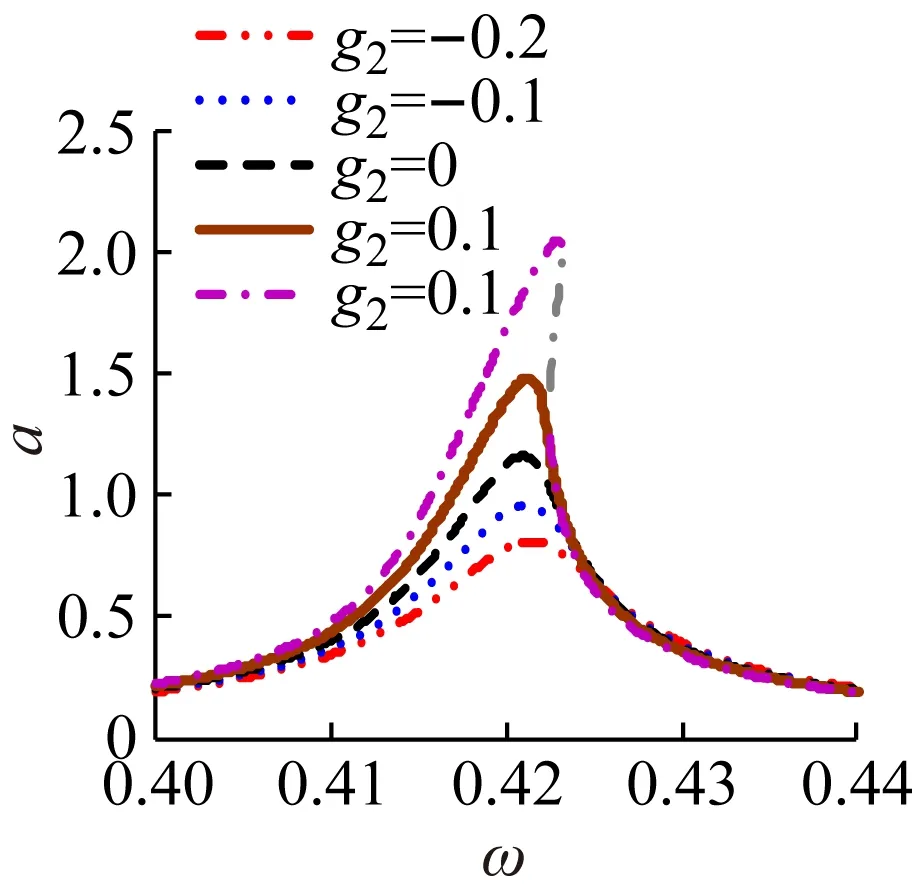
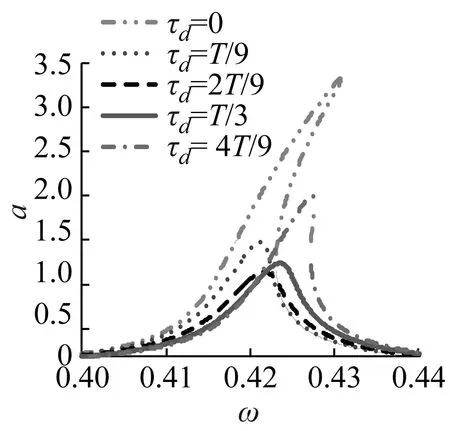
圖3為不同參數對主共振幅頻曲線的影響。在圖3(a)中，當位移控制增益g1逐漸增大時，主共振幅頻曲線向左偏移，主共振峰值頻率減小；當g1=-0.1時使主共振穩態幅值大幅增加，灰色不穩定分支大幅擴展，因此特定的g1可能導致主共振穩定性變差；而且合理的選取g1可以有效縮減主共振穩態幅值，增加系統的穩定性，如g1=0.2時，穩態幅值僅為0.94。圖3(b)表明隨著速度控制增益g2由負→正逐漸增大，主共振穩態幅值逐漸增大，而且當g2較大，如g2=0.2時，會導致系統的不穩定，因此負速度反饋增益g2能夠使主共振穩態幅值有效減小，增加系統穩定性。由圖3(c)可以看出，控制系統位移時滯τd在0～T/2內變化時，主共振穩態幅值不斷波動，特定的τd會導致主共振的不穩定，只有在τd接近T/4時齒輪系統的主共振穩態振幅值最小，此時系統具有較好的穩定性；而且也注意到隨著τd的增加，主共振骨架曲線右移，使主共振頻率增大。圖3(d)表明在當前系統中隨著速度時滯τv增加穩態幅值不斷減小，不穩定灰色分支逐漸縮聚，在τv=T/2時對主共振具有較好減振性。

(a)

(b)

(c)

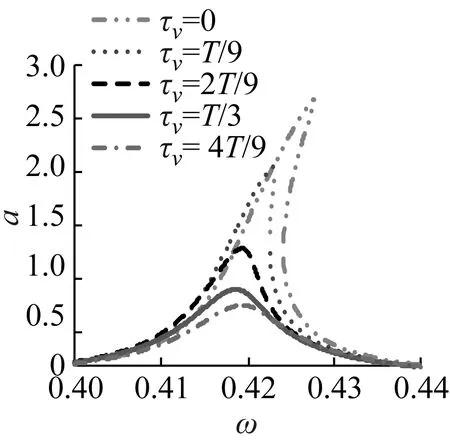
(d)圖3 不同控制參數對應的主共振幅頻響應Fig.3 The frequency response in different control parameters

(a)

(b)

(c)

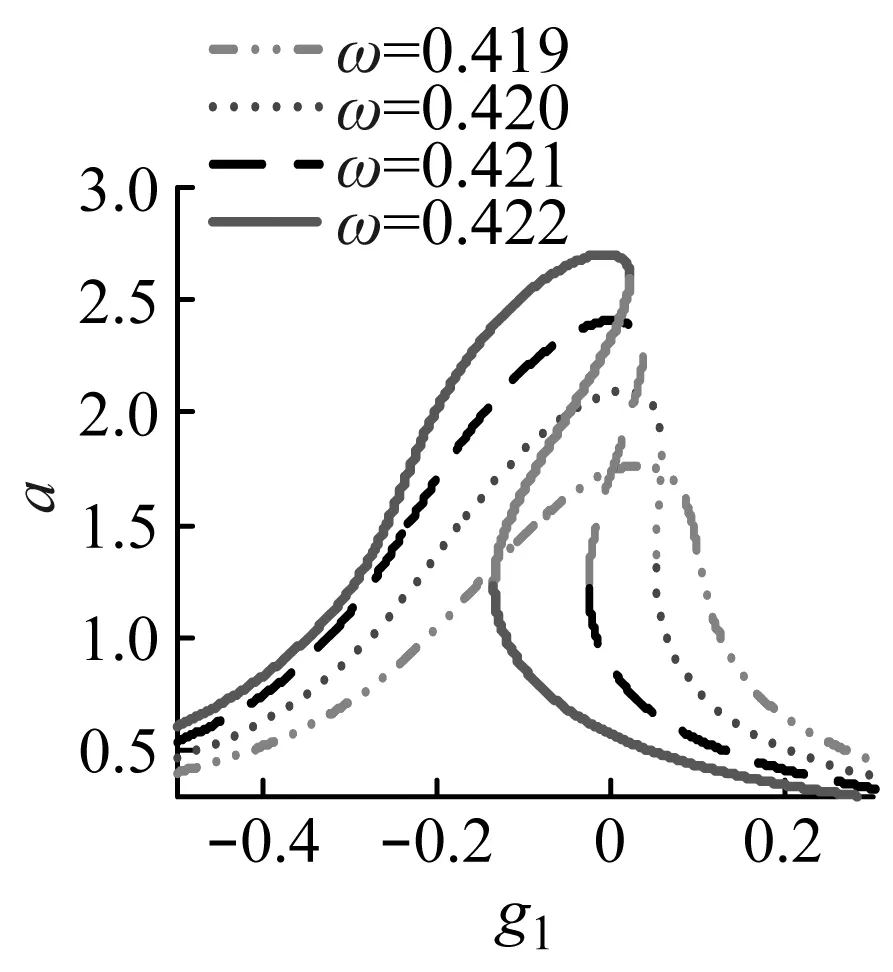
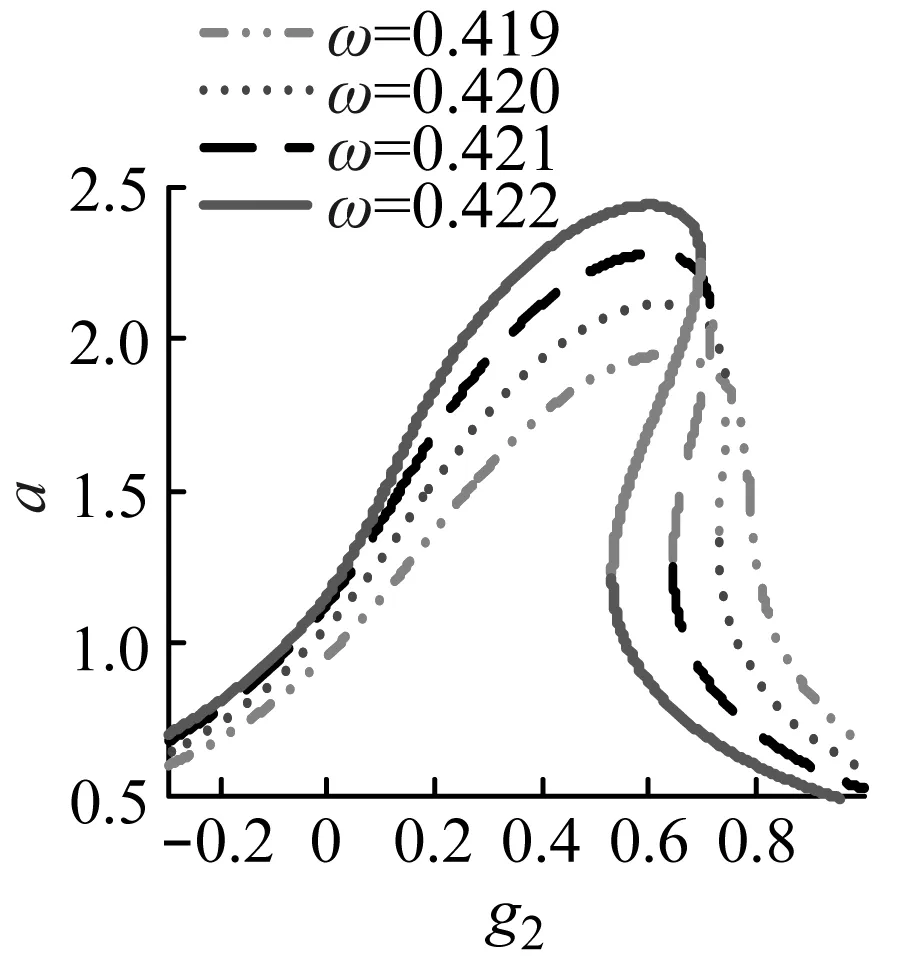
(d)圖4 控制參數對振幅的影響Fig.4 The effect of control parameters on the amplitude

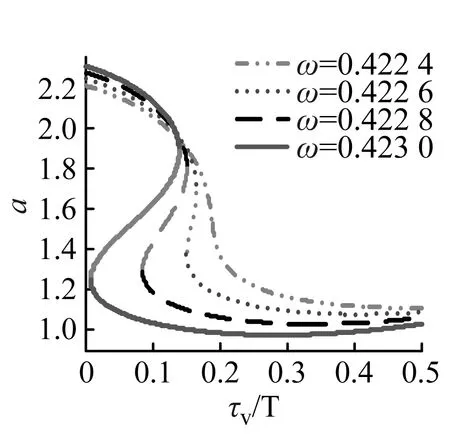
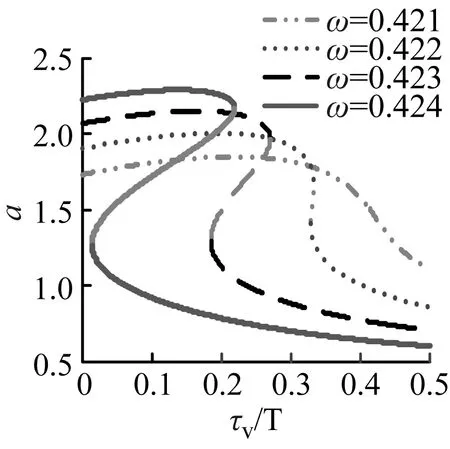
圖4是各時滯控制參數對主共振穩態幅值的影響曲線。其中圖4(a)表明位移控制增益g1在一定范圍內取值可能導致主共振穩態幅值大幅增加，當ω超過臨界頻率后，ω越大g1導致主共振不穩定的可能性越大；隨著ω的增加觸發主共振不穩定的最小g1減小，而且對于當前系統g1的絕對值在零附近時更易誘發主共振的不穩定。圖4(b)說明速度控制增益g2在一定范圍內取值也會使主共振穩態幅值增大，隨著ω的增加，g2導致主共振失穩的可能性增加，同時也注意到本系統中g2為正更易導致直齒輪主共振的失穩。在圖4(c)中可以看出，當ω小于臨界頻率時，主共振穩態幅值隨位移時滯τd增加而減小，不會引起主共振的不穩定；當ω超過臨界頻率后，τd在一定范圍內會導致主共振的穩定性變差，ω越大τd導致主共振不穩定的可能性越高，而且隨著ω的增加觸發主共振不穩定的最小時滯減小。圖4(d)表明在ω小于臨界頻率時，τv不會影響主共振的穩定性，此時只有τv較大的才會使主共振穩態幅值有效縮減；當ω大于臨界頻率后，類似于位移時滯對穩態幅值的影響，ω越高τv誘發齒輪系統的不穩定運動的可能性越大，但穩態幅值隨τv的變化趨勢與位移時滯不同。

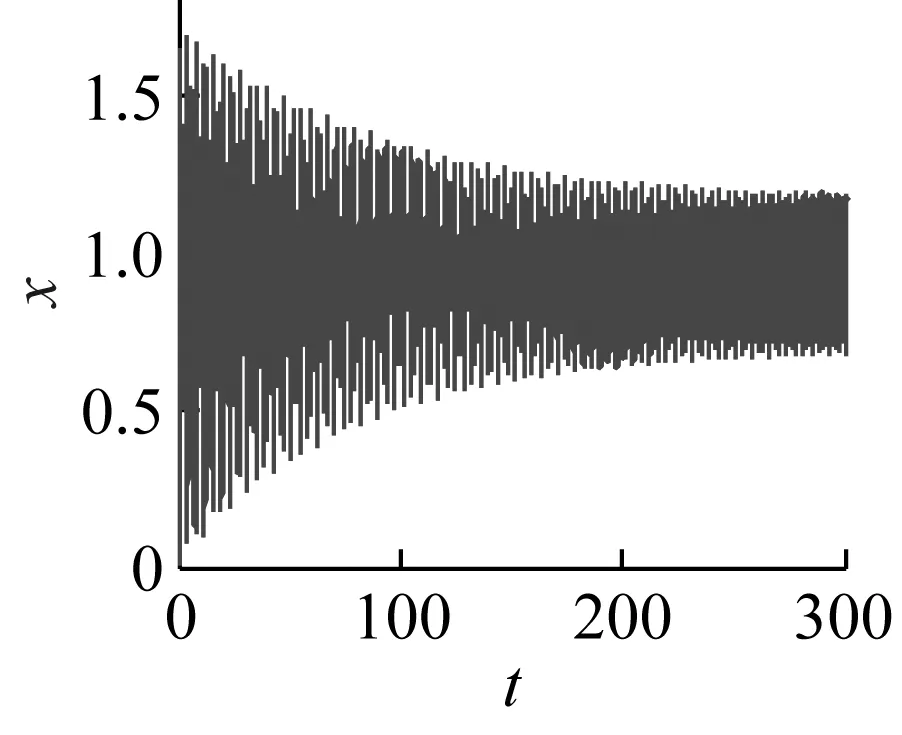
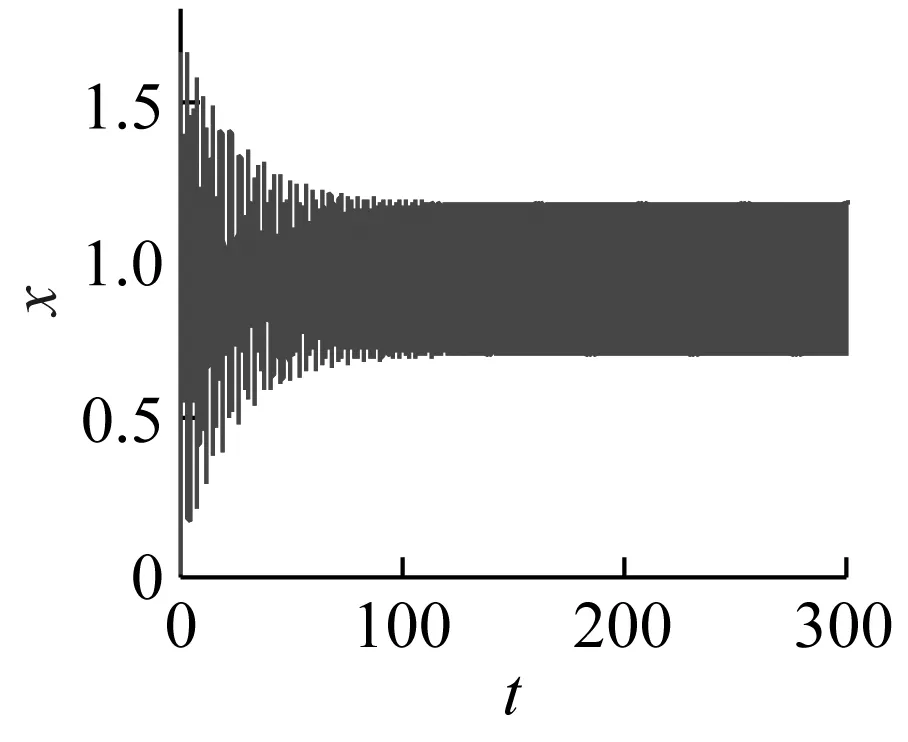
當激勵頻率ω=0.422 6時，利用Runge-Kutta法對式(6)進行數值求解，可以得到圖5(a)～(c)分別是g1=g2=0，τd=τv= 0、g1=0.2，g2=-0.2，τd=T/4，τv=T/2和g1=-0.2，g2=0.2，τd=τv=T/20時對應的時域響應和相圖。由圖5(a)可以看出，由于此時主共振不穩定，齒輪系統傳動誤差穩態在一定范圍內波動；當采用合理的時滯反饋控制后如圖5(b)所示，動態誤差快速收斂到封閉曲線上；但是在圖5(c)中，控制參數選取偏離理想值時，時滯反饋控制反而導致齒輪系統傳動誤差嚴重偏離穩定解，使動態誤差大幅增加，穩定性變差。因此齒輪系統的時滯反饋減振控制，必須選取匹配的控制參數，確保控制方法的有效性。

(a1)

(b1)

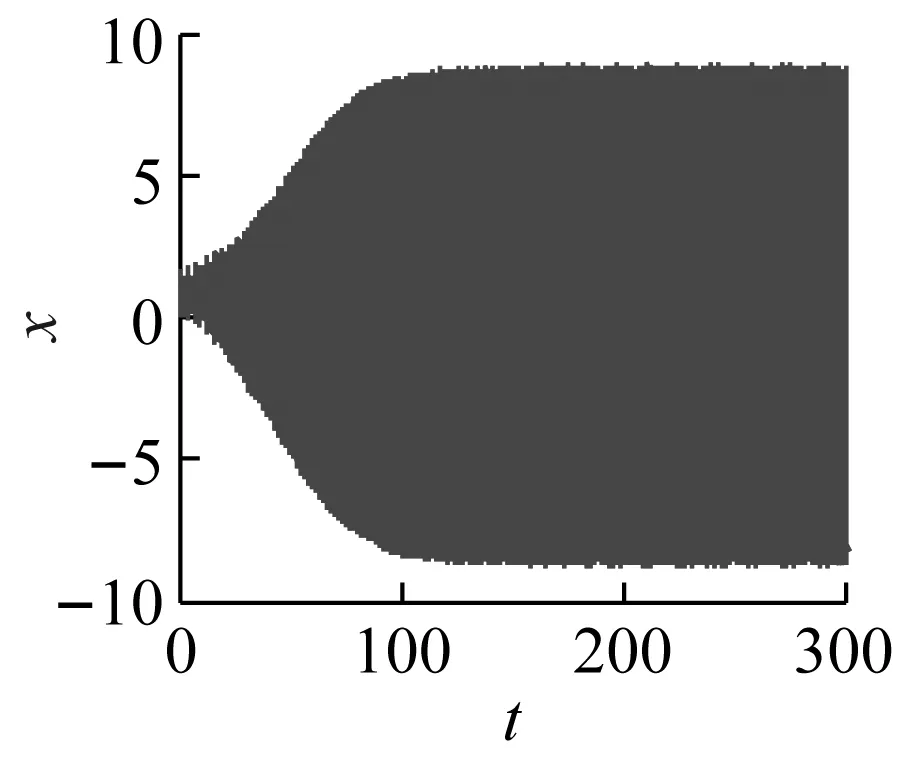
(c1)

(a2)

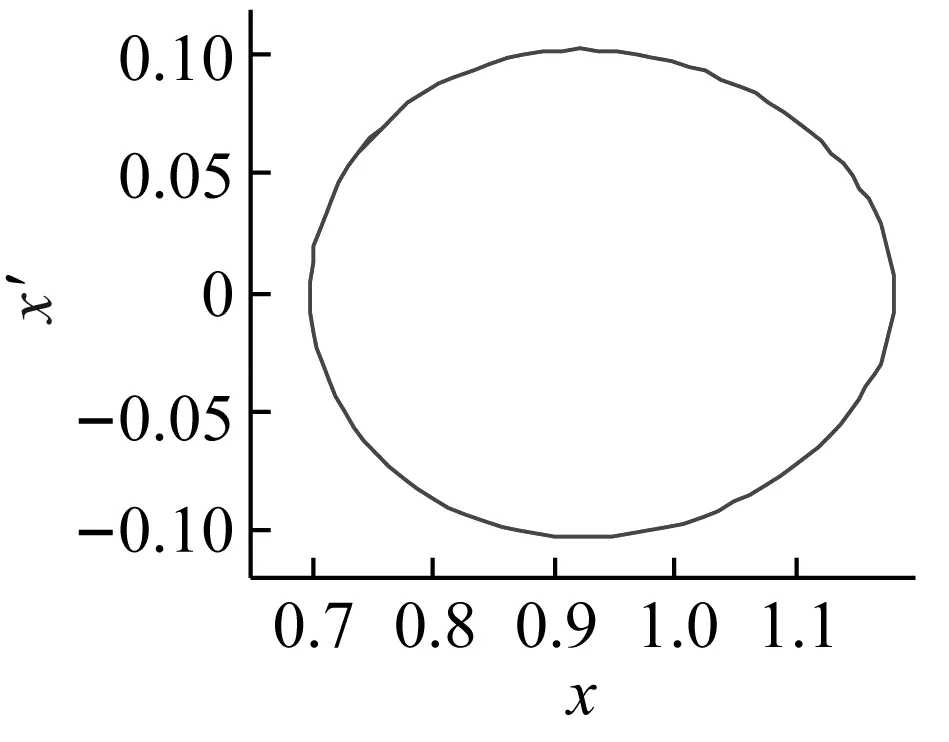
(b2)

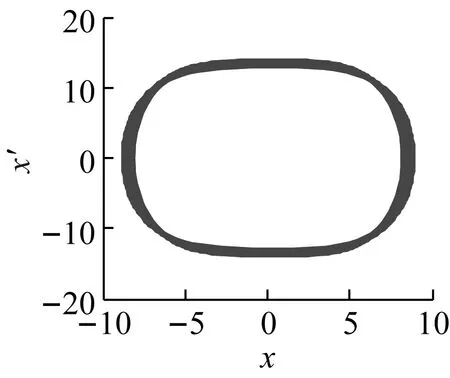
(c2)圖5 控制前后的時域響應和相平面Fig.5 The time response and phase plane before and after control

5 結 論

本文建立了含時滯反饋控制的直齒圓柱齒輪傳動系統模型，應用多尺度法和數值計算方法對系統主共振的參激振動和時域特性進行了分析，主要可以得出：

(1)載荷波動和嚙合剛度波動變化均會引起主共振的不穩定，與載荷波動不同，嚙合剛度波動增加，主共振穩態振幅減小，但較小的嚙合剛度波動也會導致系統的不穩定。

(2)位移、速度控制增益和時滯變化會引起系統主共振穩態幅值和峰值頻率變化，增加位移增益，減小速度增益，而且取τd=T/4，τv=T/2時，能夠使齒輪系統快速收斂到穩定解；

(3)一定的位移、速度增益和時滯會導致控制的不穩定，而且激勵頻率越高，控制參數觸發系統不穩定的可能性越高，控制參數的不匹配可能加劇系統振動。