基于小波能量基特征和BP 神經網絡的洗滌去污等級識別

巫志遠, 朱曉偉，王 嘉，劉建立

織物的洗滌方法有多種。其中，機洗具有一次洗滌量大、方便并具有烘干消毒等特點，織物可機洗已成為一種發展方向[1]，而織物經洗衣機洗滌后的去污效果評價也成為研究的焦點，這是洗衣機生產商關心的問題。

Manfred 等采用人工觀察法，計算每組污漬與每種織物的污漬去除指數，將其作為評價污漬去除的效率[2]。Xu 介紹了一種采用儀器的方法評估污漬等級以提高織物去污等級的精確性和可靠性[3]。在Xu 的研究中，主要采用圖像分析技術，檢索并且分割試樣圖像中的污漬區域，定義出經洗滌后反映污漬變化的指數。然后，根據AATCC 標準樣照建立織物污漬去除等級方程，用方程計算織物洗滌后去污等級從而代替人工評級。Kamalakannan 等提出了一種利用統計蛇原理的客觀評價織物去污等級的方法，將其與統計學信息結合從圖像中分割出污漬區域，并根據污漬區域大小進行評級[4]。Mao 等人介紹了一種基于Gabor濾波系數的洗滌去污客觀評價算法，并將該算法與機器視覺系統結合，實現污漬圖像的分析與污漬等級的平等[5]。Shinya 等人采用主成分分析法對污漬試樣圖像處理，以增強織物污漬區域，簡化污漬分割和識別難度[6]。沈菁等人利用掃描儀采集AATCC130-2000去污等級樣照，對5 個等級的樣照油污區域亮度值與等級關系進行回歸分析，擬合得到亮度值——去污等級方程，實現了基于沾污區域亮度值的洗滌去污等級評價[7]。為了研究小波紋理分析和BP 神經網絡在織物污漬紋理表達和洗滌去污等級識別中的可行性，本研究以4 種不同規格的織物作為對象，采用小波變換和BP 神經網絡的方法，探討基于小波能量基紋理特征的織物洗滌后去污等級的智能識別方法。

1 小波能量基特征

通過小波變換可以將織物紋理的空域信息轉變到頻域中，并且頻域的能量分布能表達空域的紋理特征，這是頻域能量特征在紋理識別中廣泛應用的基礎。能量基特征又被稱為能量特征或范數特征，具有計算量小、紋理刻畫能力強的特點。在小波系數能量基特征中，常采用1—范數和2—范數能量特征值[8]。

假設給定小波系數 ，則1 范數能量特征 和2 范數能量特征 可以表示為：

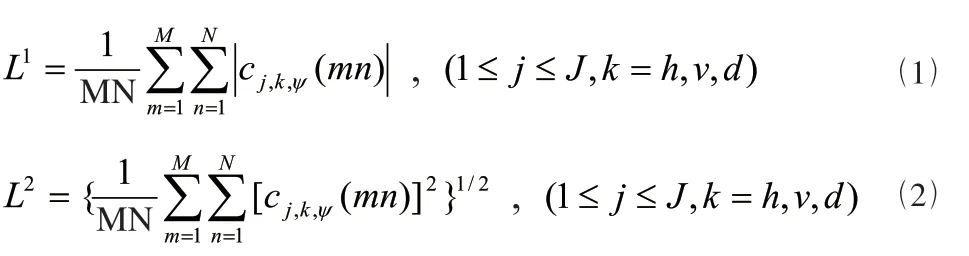
其中，j—尺度因子，即分解層數；k—平移因子，即每次小波分解后得到的3 個高頻子帶方向（水平方向h、垂直方向v、對角線方向d ）；ψ—所用的小波基函數。 MN—小波系數矩陣的大小；J—最大分解層數，可由式（3）計算：

其中，LW—濾波器長度，LS—圖像行數和列數的最大值。

因小波系數的均值為0，所以由式（1）和式（2）計算的L1和L2能量特征分別對應于小波系數絕對值的均值和方差，這是L1和L2能量特征在紋理表達中常被聯合使用的主要原因。

由小波變換原理可知，高頻子帶中僅包含油污邊界、紋理梯度銳變輪廓等強對比信息，而組織結構形成的織物細節紋理被變換到低頻子帶中[9-11]。因此，當選擇單顏色織物時，由公式（1）和（2）計算的小波能量基特征的差異是由于油污等級不同而引起的。

在本研究中，將織物洗滌去污等級識別問題看做模式識別的一個特例，采用BP 神經網絡架起由試樣提取的小波能量基特征與對應的洗滌去污等級之間的橋梁，實現兩者復雜關系的算法建模。研究思路為：織物污漬試樣圖像經過紋理特征提取，產生了一組能夠辨別不同紋理的信息，形成了洗滌去污等級識別的基礎。在洗滌去污等級識別中，本研究以BP 神經網絡為識別器，采用由公式（1）和（2）計算得到的小波能量基特征對BP 神經網絡進行訓練和測試以實現織物洗滌去污等級的智能化判別。

2 BP 神經網絡

BP 神經網絡是一種多層前饋神經網絡，包括輸入層、隱含層、輸出層，其網絡拓撲結構如圖1 所示[12]。圖1 中，X1，X2，…，Xn是BP 神經網絡的輸入值，對應于多次洗滌后的沾污試樣圖像的小波能量基特征；Y1，Y2，…，Ym是BP 神經網絡的預測值，其對應于多次洗滌后沾污試樣的去污等級。在實驗中，BP 神經網絡輸出采用0-1 編碼方式，輸出層神經元等于去污等級級別數。

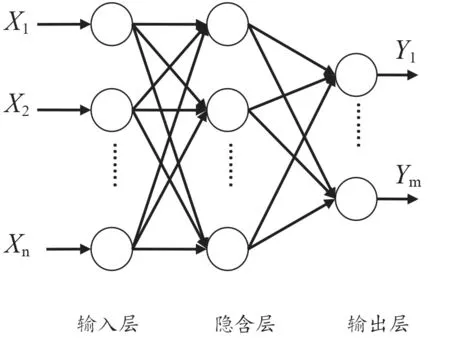
圖1 BP 神經網絡拓撲結構圖

實驗選擇4 種規格的織物按照《AATCC Test Method 130-2000 Soil Release: Oily Stain Release Method》標準規定步驟進行沾污并采用家用洗衣機進行洗滌。將洗滌后的沾污試樣與《AATCC Test Method 130-2000 Soil Release: Oily Stain Release Method》標準沾污樣照進行比較，評定洗滌去污等級。本研究選擇750 幅不同等級的洗滌沾污試樣圖像作為樣本，采用公式（1）和（2）計算每幅沾污試樣圖像的能量基小波紋理特征。

由小波變換原理可知，在分解層數不同時，可以產生的高頻子帶數量不同，即可以提取的能量基小波紋理特征數量也隨之不同。另外，每幅試樣提取的小波紋理特征的個數與BP 神經的輸入層神經元個數相等。因此，小波變換分解層數決定了每幅試樣圖像提取的特征個數和BP 神經網絡輸入層神經元個數。參照公式（1）和公式（2）可知，由L1或者L2組成的特征向量長度是對試樣圖像進行小波變換時分解層數的3 倍。若L1和L2二者聯合使用時，特征向量L12長度是小波分解層數的6 倍。相應的，BP神經網絡輸入層神經元也隨著特征向量長度的大小加以改變。按照《AATCC Test Method 130-2000 Soil Release: Oily Stain Release Method》標準的規定，洗滌去污等級分為5 個類別，等級越高，試樣沾污越少。因此，實驗中BP 神經網絡輸出層神經元個數為5。

隱含層神經元個數是影響BP 神經網絡預測性能的一個重要因素，本研究參照Kolmogorov 定理，設置隱含層神經元個數h 為:

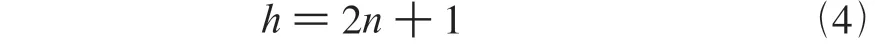
其中，n 為輸入層神經元個數。輸入層至隱含層和隱含層至輸出層的傳遞函數分別為S 型對數函數和線性函數。在BP 神經網絡訓練時，設置收斂準則為輸出均方誤差小于等于0.01，或者超過最大迭代次數200 次時，網絡停止訓練。

實驗中，洗滌沾污樣本總數為750 組。為了比較訓練樣本大小對BP 神經網絡泛化性能的影響，分別從中隨機選擇700、710、720、730 和740 個樣本作為訓練樣本訓練網絡，剩余樣本作為測試樣本檢驗網絡識別能力。

3 實驗部分

3.1 實驗方案和圖像采集

根據《ISO6330：Textiles—Domestic washing and drying procedures for textile testing》標準，設置實驗方案如表1 所示。

實驗采用4 種織物進行洗滌，使用掃描儀采集所有織物經不同次數洗滌后的圖像，并以5 等級共750幅圖像為研究對象，每個等級150 幅。圖像分辨率為1 200 dpi，存儲格式為bmp 彩色圖像。每幅圖像的大小為2 048 pixles×2 048 pixels，每塊織物對應的實際尺寸為38 cm×38 cm。圖2 所示的是實驗所用的4 種織物，圖3 是織物B 洗滌不同次數后等級從1級到5 級的圖像。

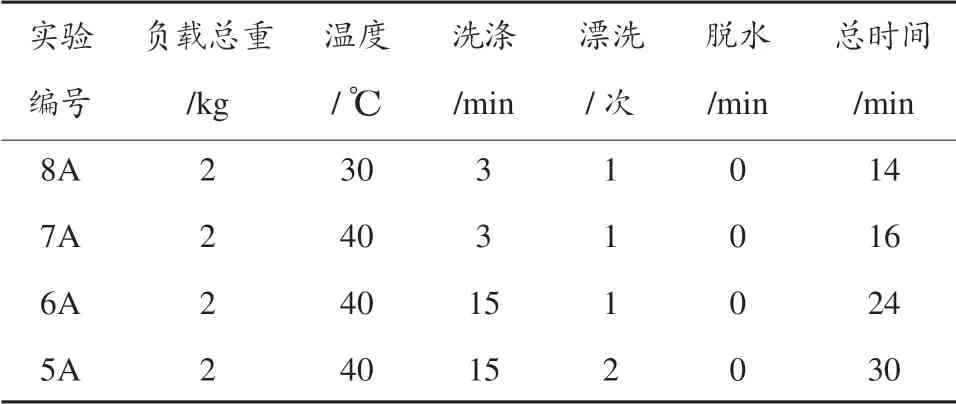
表1 實驗方案

圖2 4 種實驗試樣

圖3 織物B 洗滌后從1 級到5 級試樣圖像

3.2 實驗算法分析

本研究采用Daubechies 小波對所有圖像進行特征提取，Daubechies 小波是由世界著名小波分析學者Inrid Daubechies 構造的小波函數，一般簡寫為dbN，N 是小波的階數。小波ψ(t) 和尺度函數φ(t) 的支撐區為2N-1，ψ(t) 的消失矩為N。dbN 沒有明確的表達式（N=1 除外），但轉換函數的平方模是明確的。為了使小波分解后圖像的小波系數落在較小的支撐范圍內，N 值不能過大；為了突出油污部分的灰度突變，N 也不能太小。根據前期實驗比較發現，采用db6 小波基對試樣圖像進行重構時，可消除織物洗滌后圖像中比較光滑的背景部分，減少織物紋理對污漬區域的干擾。因此，實驗選擇db6 小波基對洗滌去污織物試樣圖像進行小波紋理分析。

在實際應用中，對圖像的分解層數一般不會超過3 層，但為了比較分解層數對提取的紋理特征的刻畫能力的影響，本研究對所有洗滌后的油污圖像進行了4 層分解。利用db6 小波對圖像進行4 層分解，得到12 個高頻子帶小波系數矩陣，根據公式(1) 和公式(2)計算各子帶小波系數矩陣的L1和L2能量基紋理特征值，形成紋理特征向量。此外，還將L1和L2聯合起來組成L12紋理特征向量。在L12中，同一高頻子帶小波系數矩陣計算的L1與L2間隔排列。每幅經多次洗滌后的沾污織物試樣的圖像的紋理特征形成一個向量，750 幅圖像的特征向量構成一個矩陣。由于分解層數不同，提取出來的紋理特征的數目也不相同。進行一層分解時，可得到水平、垂直、對角3 個方向的高頻子帶。隨著分解層數的增加，可以提取出更多的紋理特征來描述和刻畫洗滌圖像。將經小波分析提取出的750 個特征向量組成的矩陣作為樣本特征集，矩陣每列對應于一個樣本，共750 個樣本。根據圖2所示的4 種織物試樣編號，將750 個樣本分為4 組，每組試樣根據專家判別結果又分為5 個等級。在對BP 神經網絡進行訓練和測試時，從每組樣本的每個等級中按照一定比例隨機抽取訓練樣本，剩余的則為測試樣本，以保證樣本空間的廣度。

3.3 實驗結果分析

在評價BP 神經網絡的識別能力時，以正確識別率為指標，主要考慮的影響因素包括：小波變換分解層數、測試樣本個數以及紋理特征類型。其中，正確識別率為正確識別的測試樣本個數與總測試樣本個數的比值。本研究中，由于測試樣本數不同，根據紋理特征的提取算法，可得到12 個紋理特征矩陣MTF。MTF_ L12表示由L1和L2聯合組成的特征矩陣， L1_1 表示對圖像進行一層分解后的特征矩陣 L1，其他以此類推。

不同的特征矩陣對應的BP 神經網絡正確識別率如圖4 所示。從圖4 中可以看出，經BP 神經網絡訓練后，網絡的最大正確識別率為97%，當分解層數達到4 層時，3 種紋理特征矩陣對應的BP 神經網絡分類的正確識別率都超過85%，說明用小波分析對洗滌圖像進行紋理特征提取，再用BP 神經網絡對洗滌后的圖像進行分類的方法是有效的。

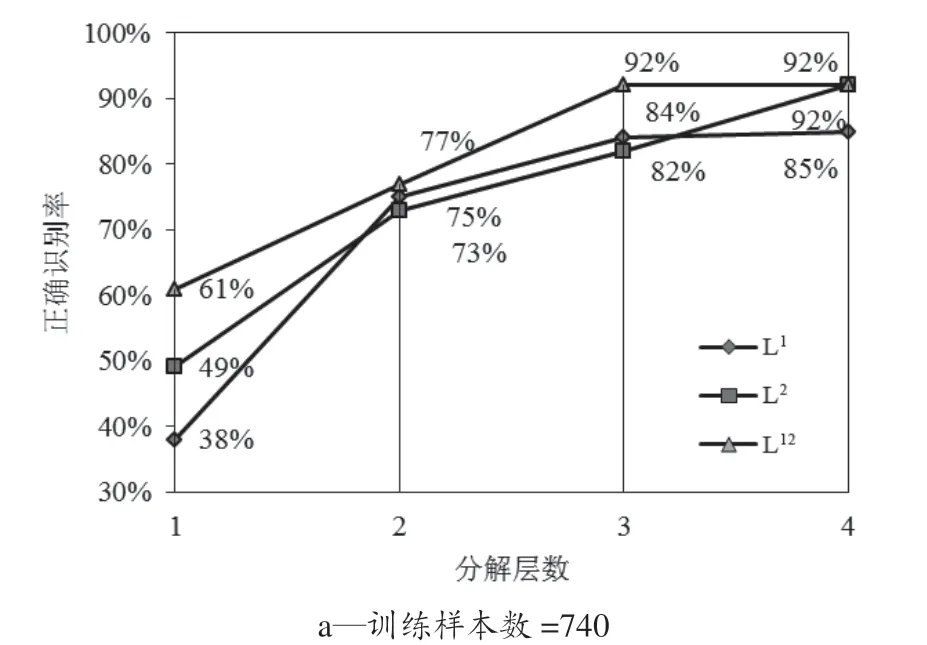
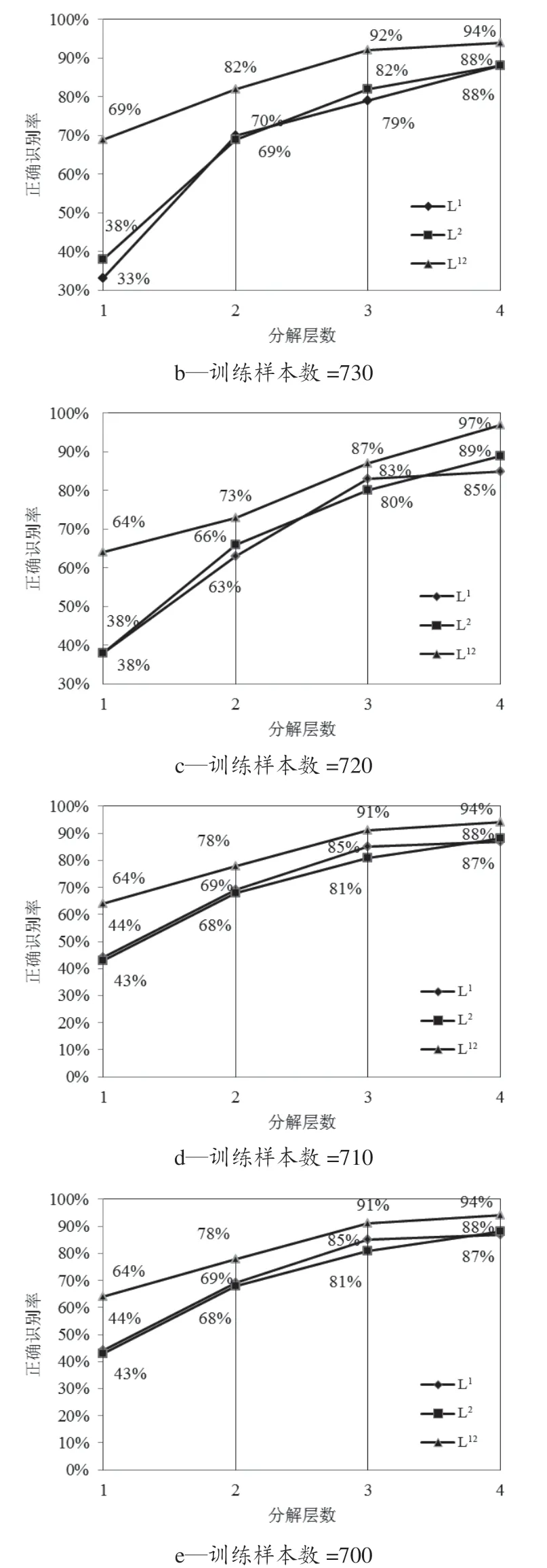
圖4 不同訓練情況下BP 神經網絡識別率

4 規律歸納

從圖4 中可以歸納出以下規律。

4.1 紋理特征數對BP 神經網絡正確識別率的影響

當測試樣本數和紋理特征矩陣保持不變時，以圖4（e）為例，分解1 層時，MTF_L1對應的正確識別率為39%，分解2 層時，正確識別率為70%，增幅為31%，分解3 層時，正確識別率為85%，增幅為15%，分解4 層時，正確識別率為88%，增幅僅為3%。隨著分解層數的增大，網絡的正確識別率也隨之增大，但是在分解4 層后，正確識別率的增幅很小甚至為零，如圖4（a）所示。若對洗滌圖像進行更多層的分解，網絡的正確識別率不會有大幅的增加，而且會增加小波紋理的分析時間以及BP神經網絡結構的復雜度。在本研究中，只對經多次洗滌后的沾污試樣圖像進行4 層分解，不再進行更多層的小波分解。MTF_ L2和MTF_ L12對應的R值的變化情況相同。

4.2 測試樣本比例對BP 神經網絡正確識別率的影響

當紋理特征類型和小波分解層數固定時，比較圖4（a）和圖4（e）的MTF_L1對應的正確識別率的變化情況。在圖4（a）和4（e）中測試樣本占總樣本的比例分別為1/75 和5/75。在小波分解層數為1 時，用10 個樣本測試后對應的BP 神經網絡正確識別率為38%，用50 個樣本測試后對應的正確識別率為39%。當小波分解層數為2 時，10 個測試樣本和50 個測試樣本對應的BP 神經網絡正確識別率分別為75%、70%。在小波分解層數為3 時，兩者對應的正確識別率分別為84% 和85%。進一步觀察，當小波分解層數為4 時，對應的正確識別率分別為85% 和88%。然而，圖4（e）對應的測試樣本比例是圖4（a）的測試樣本比例的5 倍，但是在相同分解層數下對應的BP 神經網絡對測試樣本的正確識別率都很接近。觀察圖4（b）、圖4（c）和圖4（d）可知，在相同的分解層數下，三者對應的BP 神經網絡正確識別率與（a）和（e）對應的相差不大，即在小波紋理特征類型和特征數目固定時，訓練樣本在某一區間內的變化對BP 神經網絡的正確識別率影響不大。相對而言，本實驗中測試樣本占總樣本的比例較小，在進一步的研究中將會縮小兩者級差，以系統探討測試樣本比例對正確識別率的影響。

4.3 特征種類對BP 神經網絡正確識別率的影響

當分解層數和測試樣本數不變時，以圖4（b）為例，當分解層數為1 時，MTF_L1對應的BP 神經網絡識別率為33%，MTF_L2對應的BP 神經網絡識別率為38%，兩者相差較小。然而，同樣是分解層數為1，MTF_ L12對應的BP 神經網絡識別率為69%，與MTF_L1、MTF_L2對應的正確識別率相差較大。類似的規律可以在圖4 所示的BP 神經網絡正確識別率曲線中發現，這主要是因為分解層數相同時特征向量MTF_L1和MTF_L2的長度相同，而MTF_L12是兩者的組合，其長度是MTF_L1和MTF_L2的2 倍。因此，MTF_L1和MTF_L2在同一分解層數下對應的BP 神經網絡識別率比較接近，都比MTF_L12對應的值小。但隨著分解層數的增加，MTF_L1和MTF_L2對應的BP 神經網絡正確識別率與MTF_L12對應的BP 神經網絡正確識別率之間的差值越來越小。

5 結語

本研究利用小波變換提取多次洗滌后的沾污織物試樣圖像的能量基紋理特征，并以其為輸入對BP神經網絡進行訓練和測試，進而實現沾污試樣洗滌后的洗滌去污等級預測。

實驗結果表明：基于小波紋理分析和BP 神經網絡的洗滌去污等級評價算法可以實現對多次洗滌后的沾污試樣洗滌去污等級的正確識別，最高正確識別率可達到97%。當測試樣本數和紋理特征種類保持不變時，隨著能量基小波紋理特征向量長度的增加，BP 神經網絡對試樣的洗滌去污等級的正確識別率也隨之增大，但正確識別率的增幅逐漸減小。當紋理特征類型和特征向量長度固定不變時，訓練樣本數目的變化對BP 神經網絡正確識別率的影響不顯著，正確識別率分布在相對集中的區間內。當特征向量長度和測試樣本數保持不變時，MTF_L1和MTF_L2對應的BP 神經網絡正確識別率差不多，但都小于MTF_L12對應的R值，且隨著分解層數的增加，MTF_L1和MTF_L2與MTF_L12對應的BP 神經網絡正確識別率之間的差異逐漸減小。