樁間三維土拱效應(yīng)顆粒流數(shù)值模擬及其演化規(guī)律

王桂林 冉龍寶 張亮

摘 要：抗滑樁樁間形成的土拱是水平土拱和豎向摩擦拱的共同體現(xiàn)，具有明顯的三維特征。利用顆粒流分析軟件PFC3D建立數(shù)值模型，在樁后不同高度處及同一水平面不同位置設(shè)置一系列測(cè)量球，監(jiān)測(cè)樁后土體應(yīng)力變化情況。結(jié)合顆粒位移變化情況對(duì)抗滑樁樁間三維土拱效應(yīng)的形成演化進(jìn)行分析，并對(duì)土拱厚度的演化規(guī)律做了深入研究，提出結(jié)合相對(duì)位移和最大主應(yīng)力等值線綜合確定土拱厚度的新方法。分析表明：樁后土拱由樁間臨空面靠近樁底開(kāi)始并不斷向土體內(nèi)部和上部發(fā)展，土拱的破壞過(guò)程由樁底向樁頂擴(kuò)展;土拱厚度隨深度變化表現(xiàn)為沿樁底向樁頂先增加后減小的趨勢(shì);土拱厚度隨時(shí)間的變化表現(xiàn)為隨著加載時(shí)間增加，土拱厚度先增加后減小直至土拱破壞。

關(guān)鍵詞：抗滑樁;土拱;顆粒流分析程序;演化規(guī)律;土拱厚度

中圖分類(lèi)號(hào)：TU473.1 ? 文獻(xiàn)標(biāo)志碼：A ? 文章編號(hào)：2096-6717（2019）05-0001-08

Abstract：Soil arching between anti-sliding piles is the interaction of horizontal soil arch and vertical friction arch， with distinct three-dimensional characteristics. Numerical model by the particle flow code PFC3D was developed and a series of measurement balls to numerically monitor stress variations at different positions behind the anti-slide piles were set. Combined with the displacement of numerical model balls， we analyzed the formation process and evolution pattern of the soil arching effect were analyzed. Also the thickness of soil arch had been studied and finally we proposed a new method to determine the its thickness was proposed. The study shows that the soil arch initiates s from the free face near the bottom of pile and develops to the inner and upper part of the soil， and the failure process of arch expands from the bottom of pile to the top; The thickness of soil arch varies with depth， increasing first and then decreasing along the bottom of pile to the top; The thickness of soil arch varies with time. As the loading stage proceeds， the thickness of soil arch increases first and then decreases until the soil arch is destroyed.

Keywords：anti-slide piles; soil arches; particle flow code; evolution pattern; thickness of soil arch

土拱效應(yīng)的研究與發(fā)展已經(jīng)有100多年的歷史，Roberts在1884年發(fā)現(xiàn)和提出“糧倉(cāng)效應(yīng)”，可看做拱效應(yīng)的開(kāi)端。土拱效應(yīng)最初由Terzaghi[1]提出，并通過(guò)活動(dòng)門(mén)實(shí)驗(yàn)證明了土拱效應(yīng)在巖土領(lǐng)域的存在。近年來(lái)，很多學(xué)者采用現(xiàn)場(chǎng)模擬試驗(yàn)[2]、合理拱形理論分析[3-4]和數(shù)值分析[5-7]等方法將土拱效應(yīng)理論應(yīng)用到巖土工程領(lǐng)域并取得了很好的效果。其中，抗滑樁間土拱效應(yīng)尤為明顯。

隨著計(jì)算機(jī)技術(shù)的普及與發(fā)展，運(yùn)用數(shù)值模擬進(jìn)行抗滑樁間土拱效應(yīng)作用機(jī)理研究取得了長(zhǎng)足發(fā)展。目前的研究多建立在已有合理拱軸線理論[8]上，分析各因素對(duì)樁間土拱力學(xué)效應(yīng)的影響。不少學(xué)者利用有限差分軟件和離散元軟件從二維角度分析了樁間距、土體內(nèi)摩擦角、粘聚力、孔隙比等因素對(duì)抗滑樁間土拱效應(yīng)的影響。Chen等[9]學(xué)者使用Flac有限差分軟件對(duì)群樁在側(cè)向土體運(yùn)動(dòng)作用下的成拱機(jī)理進(jìn)行了探討，解釋了應(yīng)力從土傳遞到樁的過(guò)程。張建華等[10]建立起抗滑樁結(jié)構(gòu)的有限差分模型分析了樁間距對(duì)樁間土拱效應(yīng)的的影響，研究結(jié)果對(duì)抗滑樁間距的設(shè)計(jì)有一定的參考價(jià)值。向先超等[11]利用顆粒流方法，研究了抗滑樁截面大小、間距、樁土相對(duì)變形速度和土體顆粒粒度組成對(duì)土拱效應(yīng)的影響，并揭示了這些因素對(duì)土拱的極限承載能力、殘余承載能力和樁土荷載分擔(dān)比的影響規(guī)律。Sun等 [12]采用二維顆粒流數(shù)值模型，研究了相鄰懸臂式抗滑樁間土拱的形成和破壞過(guò)程。以上研究均將樁間土拱效應(yīng)簡(jiǎn)化為二維平面問(wèn)題，但實(shí)際上樁間土拱既有水平土拱的作用，又有豎向摩擦拱的存在，三維土拱效應(yīng)明顯。近年來(lái)，對(duì)樁間土拱效應(yīng)的三維特征雖有研究[13-17]，但對(duì)三維土拱效應(yīng)的發(fā)展及土拱厚度演化規(guī)律的研究不夠深入。利用顆粒流數(shù)值模擬軟件PFC3D，分析抗滑樁間土的三維土拱效應(yīng)的形成發(fā)展及破壞過(guò)程，并對(duì)土拱厚度的演化規(guī)律進(jìn)行深入研究。

1 基本模型及參數(shù)標(biāo)定

1.1 抗滑樁三維模型

模擬抗滑樁樁間土拱的三維效應(yīng)，將樁視為剛性墻體，樁后黏性填土視為離散圓球顆粒并將顆粒間鏈接設(shè)為接觸黏結(jié)（contact bond），利用墻體來(lái)限制顆粒運(yùn)動(dòng)作為邊界約束條件（圖1），利用加載墻的運(yùn)動(dòng)來(lái)模擬土拱的形成演化過(guò)程。

模型參照董捷等[15]、王振強(qiáng)[18]等的樁間三維土拱效應(yīng)物理模型試驗(yàn)，長(zhǎng)、寬、高取為3.2 m×2.0 m×2.0 m，其中，墻后填土區(qū)尺寸為2 m×2 m×1.8 m，抗滑樁截面尺寸為0.3 m×0.3 m，樁間距取1 m，模型如圖1所示。模擬時(shí)，按照指定孔隙度生成填土范圍內(nèi)的圓球顆粒并在自重作用下壓實(shí)穩(wěn)定。文中模型宏觀參數(shù)取值詳見(jiàn)表1。

1.2 參數(shù)標(biāo)定

模擬常規(guī)三軸試驗(yàn)試件尺寸為高10 cm、半徑2.5 cm的圓柱形，模型上下設(shè)置邊界墻（wall）單元模擬加壓過(guò)程，側(cè)壁用圓柱形墻體單元（cylinder wall）模擬橡膠套筒并通過(guò)伺服保持恒定圍壓，如圖2所示。顆粒間接觸為設(shè)為接觸黏結(jié)（contact bond），通過(guò)分別施加50、75、100 kPa的圍壓得到材料的應(yīng)力應(yīng)變關(guān)系曲線，如圖3所示，對(duì)應(yīng)的偏應(yīng)力峰值強(qiáng)度分別為84、118、146 kPa。材料在3種圍壓下的摩爾強(qiáng)度包絡(luò)線[19-20]如圖4所示。

由摩爾應(yīng)力強(qiáng)度包絡(luò)曲線圖可得到數(shù)值模型的抗剪強(qiáng)度參數(shù)粘聚力和內(nèi)摩擦角分別為10 kPa和22°。最終確定模型的細(xì)觀參數(shù)如表2所示。

2 三維土拱的形成演化規(guī)律

采用三軸剪切模擬實(shí)驗(yàn)得到的細(xì)觀參數(shù)，建立抗滑樁間土拱效應(yīng)三維數(shù)值模型，取顆粒最小半徑為0.014 m，共使用約17×104個(gè)球形顆粒模擬黏性土顆粒（圖1）。模擬過(guò)程中，通過(guò)對(duì)加載墻施加大小為 0.01 m/s方向水平（y負(fù)方向）的速度來(lái)模擬下滑力對(duì)樁后土體的作用，撤去樁間擋土板計(jì)算至土體破壞。

2.1 土拱的形成與發(fā)展

土拱效應(yīng)可解釋為樁土產(chǎn)生相對(duì)位移引起的樁后土體應(yīng)力重分布現(xiàn)象，故可用土體顆粒位移量的差異來(lái)表示土拱的演化過(guò)程。付海平等[21]在樁承式路堤土拱效應(yīng)的研究中驗(yàn)證了樁土相對(duì)位移方法驗(yàn)證土拱效應(yīng)演化的可行性。本研究利用PFC內(nèi)置fish語(yǔ)言，獲得樁后土體產(chǎn)生的最大位移d，并將其分成15等份，繪制樁后土顆粒相對(duì)位移三維等值圖。

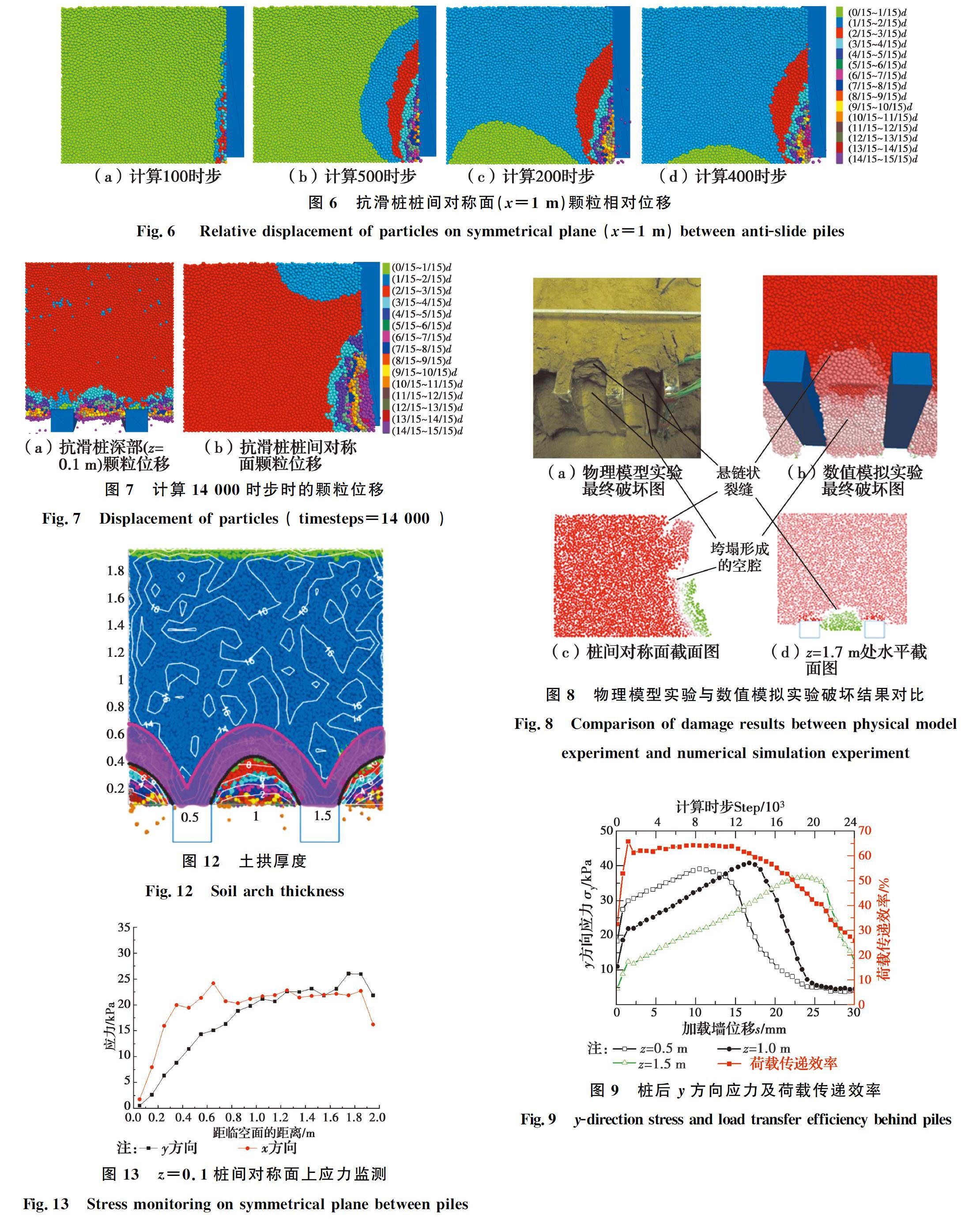
撤去樁間擋土板并給加載墻施加水平方向的速度。由于加載墻速度恒定，因此，加載墻位移與計(jì)算時(shí)步成正比關(guān)系。計(jì)算100時(shí)步（局部受壓階段）時(shí)，由圖5（a）、圖6（a）可以看到，臨空面附近土體開(kāi)始產(chǎn)生偏向樁外側(cè)的位移且樁底土體位移要多于上部，這是由于抗滑樁底部應(yīng)力較大，撤去擋土板后臨空面位置出現(xiàn)較大的應(yīng)力集中，顆粒之間相互作用力較大，樁間臨空面底部顆粒首先產(chǎn)生相對(duì)較大的變形位移，同時(shí)，樁背側(cè)土體由于樁的約束，變形幾乎為零，樁間臨空面與樁后土體變形存在差異。可以發(fā)現(xiàn)，此時(shí)樁間并沒(méi)有形成弧鏈樁的土拱形狀，表明土顆粒仍處于擠壓致密的過(guò)程;繼續(xù)運(yùn)算至500時(shí)步時(shí)，根據(jù)圖5（b）、圖6（b）可以看到樁間土顆粒與樁背土位移之間出現(xiàn)了較大的分異。具體表現(xiàn)為自抗滑樁內(nèi)側(cè)邊緣起形成較為直觀的弧鏈狀位移分層。同時(shí)，通過(guò)圖6（b）可看到相對(duì)位移的差別沿高度也有很好的辨識(shí)度，認(rèn)為此時(shí)樁間土拱已經(jīng)開(kāi)始形成;計(jì)算至2 000時(shí)步時(shí)，通過(guò)圖5（c）、圖6（c）可觀察到相對(duì)位移為（2/15～3/15）d的土顆粒分層明顯向土體內(nèi)部延伸，計(jì)算至4 000時(shí)步時(shí)，土顆粒相對(duì)位移分組與2 000時(shí)步時(shí)相比沒(méi)有太大變化，表明此段時(shí)間內(nèi)土拱處于穩(wěn)定發(fā)展階段。

2.2 土拱的破壞

繼續(xù)計(jì)算至14 000時(shí)步時(shí)，由圖7（a）、（b）可以看到，樁間弧鏈狀土拱層不再完整，從樁間對(duì)稱(chēng)面上可以看到臨空面附近出現(xiàn)較大的斷裂，表明土體已超過(guò)極限平衡狀態(tài)，原來(lái)形成的穩(wěn)定土拱遭到破壞。

繼續(xù)運(yùn)算，直至樁后土體出現(xiàn)垮塌，如圖8所示，可以看到數(shù)值模擬得到的樁后土體破壞情況與物理模型實(shí)驗(yàn)所得結(jié)果相同，均表現(xiàn)為中下部土體率先開(kāi)裂并垮塌形成空腔，頂部出現(xiàn)懸鏈狀裂縫并伴有土體下陷垮塌的跡象。產(chǎn)生這一現(xiàn)象的原因是，在下滑推力不斷增加的過(guò)程中，中下部土體產(chǎn)生的應(yīng)力相對(duì)較大，而不同位置處相同土體的極限抗剪強(qiáng)度是相同的，因而中下部土體將率先出現(xiàn)開(kāi)裂。臨空面附近土體由于缺少約束，在自重作用下將不斷地垮塌，最終形成貫通的滑動(dòng)面。

為了更直觀地分析三維土拱的演化過(guò)程，在樁后高度z為0.5、1.0、1.5 m處分別設(shè)置應(yīng)力監(jiān)測(cè)球，監(jiān)測(cè)樁后y方向的應(yīng)力隨加載墻位移的變化情況，與此同時(shí)，用抗滑樁承受的土壓力與加載墻承受的壓力之比表示荷載傳遞效率，荷載傳遞效率越高，則樁間三維土拱效應(yīng)越顯著。監(jiān)測(cè)結(jié)果見(jiàn)圖9。

圖9中樁后不同深度處y方向的應(yīng)力監(jiān)測(cè)顯示，填土底部（z=0.5 m）處的應(yīng)力監(jiān)測(cè)在加載墻位移達(dá)到12 mm后開(kāi)始急劇減少，該位置形成的土拱此刻已達(dá)極限狀態(tài);抗滑樁中部（z=1.0 m）處的應(yīng)力在加載墻位移達(dá)18 mm左右時(shí)開(kāi)始下降，抗滑樁上部（z=1.5 m）在加載墻位移達(dá)25 mm時(shí)才開(kāi)始下降，表明土拱的破壞是從抗滑樁底部開(kāi)始，逐漸向上發(fā)展的。

2.3 土拱效應(yīng)階段劃分

根據(jù)圖9所示的樁后y方向應(yīng)力及荷載傳遞效率監(jiān)測(cè)結(jié)果，結(jié)合土拱的形成演化過(guò)程分析，將土拱的形成發(fā)展分為3階段：土拱初步形成階段、土拱穩(wěn)定發(fā)展階段和土拱破壞階段。

土拱初步形成階段：樁土相對(duì)位移較小，樁后土體局部受壓，隨著樁土相對(duì)位移不斷擴(kuò)大，樁背側(cè)土體受到阻攔，且范圍不斷擴(kuò)大，臨近土體相互鍥緊，并向后側(cè)土體發(fā)展，形成具有較高承載力的且沿樁身均有分布的拱形結(jié)構(gòu)，將此階段定義為土拱初步形成階段。此階段的特點(diǎn)是樁后土體應(yīng)力增加較快，荷載傳遞效率呈增加的趨勢(shì)。此階段出現(xiàn)在加載初期，加載墻位移不足2 mm時(shí)。

土拱穩(wěn)定發(fā)展階段：土拱雛形形成后，隨著加載墻位移的繼續(xù)增加，拱后土體密實(shí)度增加，土拱作用進(jìn)一步增強(qiáng)。此階段的特點(diǎn)是樁后應(yīng)力增長(zhǎng)變緩，荷載傳遞效率基本保持不變。該階段持續(xù)時(shí)間較長(zhǎng)，出現(xiàn)在加載墻位移達(dá)約2～15 mm期間。

土拱破壞階段：土拱穩(wěn)定階段發(fā)展到后期，隨著加載墻位移不斷增大，土拱進(jìn)一步擠密，達(dá)到土體抗剪強(qiáng)度，土拱發(fā)生破壞。此階段的特點(diǎn)是樁后應(yīng)力突然減小，荷載傳遞效率呈現(xiàn)降低的趨勢(shì)。該階段出現(xiàn)在加載墻位移達(dá)到約15 mm后。

3 土拱厚度的演化規(guī)律

3.1 土拱厚度確定

土拱效應(yīng)的產(chǎn)生與樁土間的相對(duì)位移密不可分，拱身部分土體在鍥緊作用下密實(shí)度較高，而臨空面附近由于沒(méi)有約束，土顆粒位移較大，拱身和拱前土體可能會(huì)產(chǎn)生較大的相對(duì)位移，發(fā)展到后期甚至出現(xiàn)裂紋或形成貫通的滑動(dòng)面，故可用土體顆粒相對(duì)位移來(lái)確定土拱前緣。

取土拱穩(wěn)定發(fā)展階段（s=5 mm）的土拱效應(yīng)進(jìn)行分析。現(xiàn)選取距樁底部z=0.1 m處的水平截面，用相對(duì)位移確定土拱范圍的前緣。土拱前緣開(kāi)始于抗滑樁內(nèi)側(cè)邊緣，向內(nèi)部土體延伸，如圖10所示。土拱前緣線大致呈懸鏈狀，左右對(duì)稱(chēng)。

懸臂式抗滑樁土拱效應(yīng)的空間特征十分顯著，按照土拱的作用面將其分成水平拱、豎向拱和臨空面拱。其中，水平面拱為大主應(yīng)力偏轉(zhuǎn)形成的大主應(yīng)力拱并認(rèn)為拱軸線上主應(yīng)力處處相等，即拱軸線也是大主應(yīng)力等值線。基于此假定，可以利用大主應(yīng)力等值線確定土拱后緣。通過(guò)導(dǎo)出顆粒流數(shù)值模型中的應(yīng)力張量，利用MATLAB求解最大主應(yīng)力并生成二維等值線圖，如圖11所示。可以發(fā)現(xiàn)最大主應(yīng)力等值線在臨空面附近發(fā)生了偏轉(zhuǎn)，等值線呈現(xiàn)出一系列的弧形狀排列，且靠近臨空面時(shí)等值線較密集，遠(yuǎn)離臨空面達(dá)到一定距離后，等值線變得稀疏直至不具有明顯特征。以樁后應(yīng)力集中位置為起點(diǎn)，參考等值線的稀疏分布及規(guī)律，向兩邊延伸形成的光滑弧形拱作為土拱的后緣。

將由上述方法確定土拱的前緣和后緣綜合繪制在圖12上，可以看到土拱前緣后緣形狀基本相似，形成與樁寬大致相等（0.3 m）的等厚土拱。

在樁間對(duì)稱(chēng)面上z=0.1 m位置處設(shè)置一排監(jiān)測(cè)點(diǎn)監(jiān)測(cè)各點(diǎn)的x方向和y方向應(yīng)力情況。當(dāng)土拱效應(yīng)發(fā)揮時(shí)，應(yīng)力沿拱軸線方向傳遞到樁后，在樁間對(duì)稱(chēng)面上表現(xiàn)為x方向應(yīng)力突變，在土體內(nèi)部，由于加載墻的移動(dòng)，y方向應(yīng)力基本保持不變，靠近土拱效應(yīng)發(fā)揮區(qū)域時(shí)，應(yīng)力發(fā)生偏轉(zhuǎn)，y方向應(yīng)力將突然變小，利用這一特性可以檢驗(yàn)前述方法的合理性。 ?由圖13可以發(fā)現(xiàn)，x方向應(yīng)力變化趨勢(shì)減緩發(fā)生在距離臨空面約0.3 m處，y方向應(yīng)力變化趨勢(shì)減緩發(fā)生在距離臨空面約0.8 m處，與圖12確定的土拱范圍基本一致，說(shuō)明采用前述方法確定土拱效應(yīng)的拱厚度是可行的。

3.2 土拱厚度隨深度的變化規(guī)律

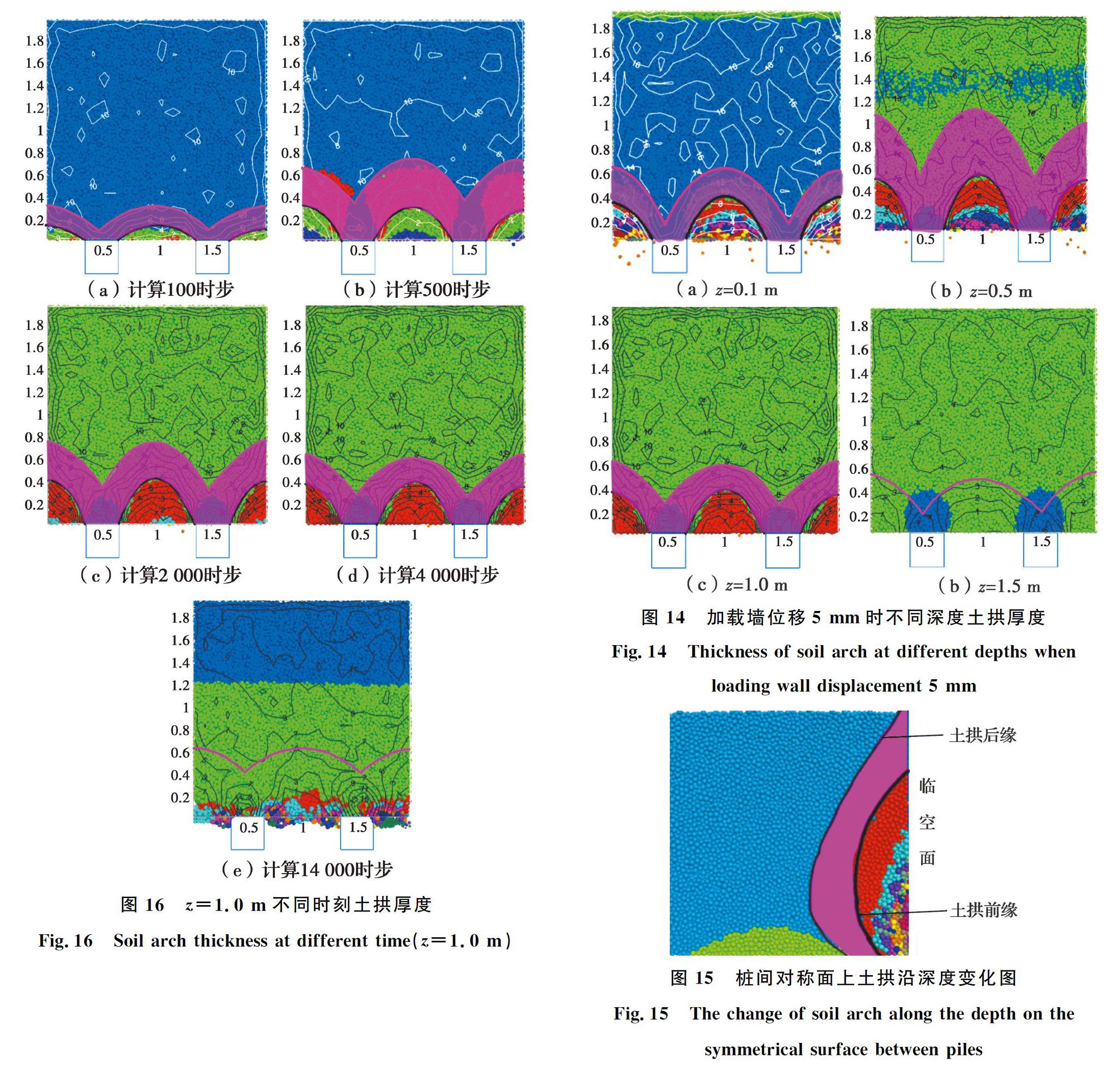
在土拱穩(wěn)定發(fā)展階段，計(jì)算時(shí)步為4 000時(shí)步時(shí)，（加載墻位移約5 mm）分別取距樁底部0.1、0.5、1.0、1.5 m處的水平截面按照3.1節(jié)的方法確定土拱厚度，如圖14所示。

根據(jù)圖14可知，土拱厚度是隨深度變化的。為了更明顯地顯示土拱厚度隨深度的變化情況，通過(guò)分析多個(gè)不同深度水平剖面的土拱厚度分布，作出樁間對(duì)稱(chēng)面土拱厚度隨深度變化圖，如圖15所示。在樁底位置時(shí)，土拱厚度相對(duì)較薄，這是因?yàn)闃兜孜恢贸丝够瑯秾?duì)土體有阻擋約束作用外，部分應(yīng)力通過(guò)下層土體傳遞到樁前土（模型中由底部固定邊界摩擦承擔(dān)），因此，土拱效應(yīng)相對(duì)較弱;土體更容易產(chǎn)生較大位移，土拱效應(yīng)更加明顯。樁頂位置由于土體應(yīng)力較小，顆粒產(chǎn)生的位移量更小，土拱厚度相對(duì)較薄。由于采取的模型中設(shè)置了加載墻以便模擬土拱的破壞，使得樁土相對(duì)位移量比自然狀態(tài)下的邊坡樁土相對(duì)位移更大，土拱的厚度與實(shí)際情況相比也要偏大。

3.3 土拱厚度隨時(shí)間的變化規(guī)律

由于數(shù)值模型設(shè)置的加載墻一直在運(yùn)動(dòng)中，表現(xiàn)為樁后下滑力一直處在變化中，故土拱厚度隨時(shí)間的變化規(guī)律更多的表現(xiàn)為土拱厚度在演化過(guò)程中的變化規(guī)律。

取計(jì)算時(shí)步為100、500、2 000、4 000、14 000分析樁后土拱效應(yīng)隨時(shí)間的演化。以抗滑樁中部（z=1.0 m）水平截面為例進(jìn)行分析，結(jié)果如圖16所示。

圖16的結(jié)果表明，土拱的厚度在土拱的形成演化過(guò)程中也是在變化的。在最開(kāi)始計(jì)算的100時(shí)步時(shí)，樁后土體處于局部受壓狀態(tài)，樁間土體位移相對(duì)較小，土拱效應(yīng)較弱，形成的土拱僅在臨空面附近0.35 m范圍內(nèi)，且厚度較薄;計(jì)算至500時(shí)步時(shí)，樁間土體處于土拱初步形成階段，樁間土體相對(duì)位移增大，土拱的前后緣均向土體內(nèi)部延伸，土拱的影響范圍擴(kuò)展至臨空面附近0.8 m范圍內(nèi)，土拱厚度增加;計(jì)算至2 000時(shí)步時(shí)，樁間土體處于土拱穩(wěn)定發(fā)展階段，土拱前緣向土體內(nèi)部產(chǎn)生較小的延伸，土拱厚度變薄，繼續(xù)計(jì)算至4 000時(shí)步時(shí)，土拱厚度進(jìn)一步變薄，土拱后緣朝臨空面附近靠近，產(chǎn)生這一變化的原因是，土拱穩(wěn)定發(fā)展過(guò)程中，土拱形狀基本確定，前緣經(jīng)鍥緊作用壓密，而后側(cè)土體還有壓縮的空間，隨著加載墻位移的增加，土拱影響范圍內(nèi)的土體不斷壓密導(dǎo)致最大主應(yīng)力等值線向臨空面附近靠近，土拱厚度變薄;繼續(xù)計(jì)算至14 000時(shí)步時(shí)，土拱處于破壞狀態(tài)，由圖16（b）可看到，此時(shí)的土拱范圍與土拱穩(wěn)定發(fā)展階段的大不相同，前緣土體已經(jīng)破壞，土拱前緣已不存在。

綜上所述，在土拱的形成演化過(guò)程中，土拱的厚度具有明顯的空間與時(shí)間變化規(guī)律。目前，對(duì)于土拱厚度的認(rèn)知公認(rèn)的是假定土拱厚度等于樁寬或者為樁寬的一半。這種做法顯然具有一定局限性，首先，樁后不同深度處或者不同階段時(shí)土體受力狀態(tài)不同，所形成的土拱厚度也不同。當(dāng)土拱處于穩(wěn)定階段時(shí)，土拱的厚度與樁寬相差不大，表明在精度要求不高的情況下，將樁寬作為土拱厚度也是可行的。

4 結(jié)論

依據(jù)已有的樁間三維土拱效應(yīng)物理模型試驗(yàn)，選取合理的模型尺寸與參數(shù)進(jìn)行三維顆粒流模擬研究，得出以下結(jié)論：

1）把抗滑樁當(dāng)作剛性樁時(shí)，撤去抗滑樁間擋土板后樁底的土體首先產(chǎn)生位移，之后不斷向土體內(nèi)部和樁頂發(fā)展;土拱的破壞首先出現(xiàn)在樁底位置，并逐漸向樁頂發(fā)展。

2）土拱厚度隨深度是變化的，具體表現(xiàn)為樁底位置土拱厚度較小，中部土拱厚度最大，樁頂位置較薄。

3）土拱厚度在滑體推力施加過(guò)程中是變化的。隨著加載墻位移的增加，土拱厚度經(jīng)歷了由薄變厚再變薄的變化過(guò)程。

參考文獻(xiàn)：

[1] TERZAGHI K. Theoretical soil mechanics[M]. New York： John Wiley & Son， 1943.

[2] 王桂林， 樊友全， 張永興，等. 抗滑樁土拱效應(yīng)的時(shí)效性試驗(yàn)分析[J]. 土木建筑與環(huán)境工程， 2011， 33（2）：28-31.

WANG G L， FAN Y Q， ZHANG Y X， et al. Time effect experimental analysis of the soilarch effect of anti-sliding pile[J]. Journal of Civil， Architectural & Environmental Engineering， 2011， 33（2）：28-31. （in Chinese）

[3] CHENG S G. Properties of soil arching between piles and reasonable distance of piles in slope engineering[C]//2011 International Conference on Electric Information and Control Engineering， Wuhan， China， 2011： 1557-1559.

[4] WANG R H， ZHOU H Q. Analysis of the soil arch effect of the mechanical rotary bored anti-slide piles and ultimate arch thickness calculation[J]. Modelling， Measurement and Control B， 2017， 86（2）： 502-516.

[5] LAI H J， ZHENG J J， ZHANG R J， et al. Classification and characteristics of soil arching structures in pile-supported embankments[J]. Computers & Geotechnics， 2018， 98：153-171.

[6] 郭紅梅. 樁承式路堤土拱效應(yīng)顆粒流分析[J]. 土木建筑與環(huán)境工程， 2014， 36（6）：87-93.

GUO H M. DEM analysis of soil arching of pile supported embankment[J]. Journal of Civil， Architectural & Environmental Engineering， 2014， 36（6）：87-93. （in Chinese）

[7] RUI R， TOL F V， XIA X L， et al. Evolution of soil arching; 2D DEM simulations[J]. Computers & Geotechnics， 2016， 73：199-209.

[8] 賈海莉， 王成華， 李江洪. 關(guān)于土拱效應(yīng)的幾個(gè)問(wèn)題[J]. 西南交通大學(xué)學(xué)報(bào)， 2003， 38（7）：398-402.

JIA H L， WANG C H， LI J H. Discussion on some issues in theory of soil arch[J]. Journal of Southwest Jiaotong University， 2003， 38（7） ：398-402. （in Chinese）

[9] CHEN C Y， MARTIN G R. Soil-structure interaction for landslide stabilizing piles[J]. Computers & Geotechnics， 2002， 29（5）：363-386.

[10] 張建華， 謝強(qiáng)， 張照秀. 抗滑樁結(jié)構(gòu)的土拱效應(yīng)及其數(shù)值模擬[J]. 巖石力學(xué)與工程學(xué)報(bào)， 2004， 23（4）： 699-703.

ZHANG J H， XIE Q， ZHANG Z X. Arching effect of anti-slide pile structure and its numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23（4）： 699-703.（in Chinese）

[11] 向先超， 張華， 蔣國(guó)盛， 等. 基于顆粒流的抗滑樁土拱效應(yīng)研究[J]. 巖土工程學(xué)報(bào)， 2011， 33（3）：386-391.

XIANG X C， ZHANG H， JIANG G S， et al. Soil arching effect of anti-slide piles based on particle flow method[J]. Chinese Journal of Geotechnical Engineering， 2011， 33（3）：386-391. （in Chinese）.

[12] SUN J S， JIN X B. Soil arching forming and failure mechanism between adjacent cantilever anti-slide pile[J]. Electronic Journal of Geotechnical Engineering， 2015， 20（16）：9665-9673.

[13] 蔣建平， 姚均東. 滑體為黏土層的懸臂式抗滑樁三維土拱效應(yīng)研究[J]. 應(yīng)用基礎(chǔ)與工程科學(xué)學(xué)報(bào)， 2017， 25（5）：1011-1025.

JIANG J P， YAO J D. Study on three dimensional soil arch effect of cantilever piles for stabilizing slope with clay sliding mass[J]. Journal of Basic Science and Engineering， 2017， 25（5）：1011-1025. （in Chinese）

[14] 姜春林， 李晉. 微型抗滑樁土拱效應(yīng)空間特征的細(xì)觀力學(xué)分析[J]. 巖土力學(xué)， 2012， 33（6）：1754-1815.

JIANG C L， LI J. Mesomechanical analysis of spatial characteristics of soil arching effect on micro anti-slide pile system[J]. Rock and Soil Mechanics， 2012， 33（6）：1754-1815. （in Chinese）

[15] 董捷， 張永興， 文海家， 等. 懸臂式抗滑樁三維土拱效應(yīng)研究[J]. 工程勘察， 2009， 37（3）： 5-10，30.

DONG J， ZHANG Y X， WEN H J， et al. Research on three-dimensional soil arching effect between cantilever anti-slide piles[J]. Journal of Geotechnical Investigation & Surveying， 2009， 37（3）： 5-10，30.（in Chinese）

[16] FU X， XIE Q. Spatial distribution of soil pressure based on soil arching effect of full-buried anti-slide pile[J]. Electronic Journal of Geotechnical Engineering， 2013， 18：5193-5202.

[17] BAKRI M， XIA Y Y， WANG H B. Load sharing of anti slide piles based on three dimensional soil arching numerical analysis[J]. Electronic Journal of Geotechnical Engineering， 2014， 19（Z6）：17573-17590.

[18] 王振強(qiáng). 懸臂抗滑樁土拱效應(yīng)的靜力及動(dòng)力特性研究[D]. 重慶： 重慶大學(xué)， 2014.

WANG Z Q. Study on static and dynamic characteristics of soil arching effect of cantilever piles[D]. Chongqing： Chongqing University， 2014.（in Chinese）

[19] LIAN C Q， ZHUGE Y， BEECHAM S. Numerical simulation of the mechanical behaviour of porous concrete [J]. Engineering Computations， 2011， 28（8）： 984-1002

[20] 邢煒杰， 余湘娟， 高磊， 等. 基于顆粒流離散元的黏性土三軸剪切試驗(yàn)數(shù)值模擬[J]. 科學(xué)技術(shù)與工程， 2017， 17（35）： 119-124.

XING W J， YU X J， GAO L， et al. Numerical simulation of cohesive soil triaxial shear test based on particle flow discrete element[J]. Science Technology and Engineering， 2017， 17（35）： 119-124.（in Chinese）

[21] 付海平， 鄭俊杰， 賴(lài)漢江， 等. 樁承式路堤 “土拱結(jié)構(gòu)” 形成演化規(guī)律離散元分析[J]. 巖土工程學(xué)報(bào)， 2017， 39（11）： 2050-2057.

FU H P， ZHENG J J， LAI H J， et al. Discrete element analysis of the development and evolution of “soil arching” within a piled embankment[J]. Chinese Journal of Geotechnical Engineering， 2017， 39（11）： 2050-2057.（in Chinese）

（編輯 胡玲）