表面織構對水潤滑軸承混合潤滑性能的影響*

(北京理工大學機械與車輛學院 北京100081)

船舶尾軸是船舶動力裝置與螺旋槳之間能量傳遞的重要系統，其中尾軸軸承起著支承螺旋槳尾軸的作用，對軸系能否安全可靠工作起著關鍵作用。大多數尾軸軸承采用開式水潤滑系統，即直接使用海水或河水作為潤滑介質。由于水的理化特性不同于礦物質油，其作為潤滑介質存在如下問題[1]：水的黏度小、承載力不高，不易形成流體動壓潤滑，因而容易造成摩擦副間的直接接觸；此外水更易發生空化現象，亦會對軸承造成極大的破壞。針對上述問題，HE等[2]建立螺旋槳軸承混合潤滑模型，分析了考慮軸的彎曲和不同空化條件下的水潤滑軸承性能；KRAKER等[3]建立了水潤滑軸承彈流潤滑模型，利用有限差分法計算了在一定負載下摩擦副間的接觸壓力。

表面織構被認為是改善油潤滑摩擦副潤滑性能的一種有效手段，其原理是表面上的微坑或微溝槽可以充當微流體動壓潤滑軸承，所產生的附加流體動壓力能夠有效避免摩擦副表面的直接接觸，從而減小摩擦[4]。但將表面織構用于水潤滑軸承的研究甚少，目前的相關研究多為全膜潤滑情形[5]，缺乏表面織構對水潤滑軸承混合潤滑性能影響的研究。

為此，本文作者建立了JFO空化邊界條件下具有表面織構的水潤滑軸承混合潤滑模型并數值求解，以獲得不同織構參數下的Stribeck曲線，分析不同織構參數對水潤滑軸承潤滑狀態的影響。

1 數學模型

圖1所示為文中研究的水潤滑滑動軸承，其軸套內表面加工了一系列規則排列的表面織構。由于水的黏度較低，并假設軸承完全沉浸在水中，因此在潤滑分析中可以不考慮壓力及溫度變化對水的黏度和密度的影響。圖1中ω為軸頸的旋轉角速度，e為偏心距，ε=e/c，ε、c分別為偏心率和半徑間隙，y代表軸承軸向方向。

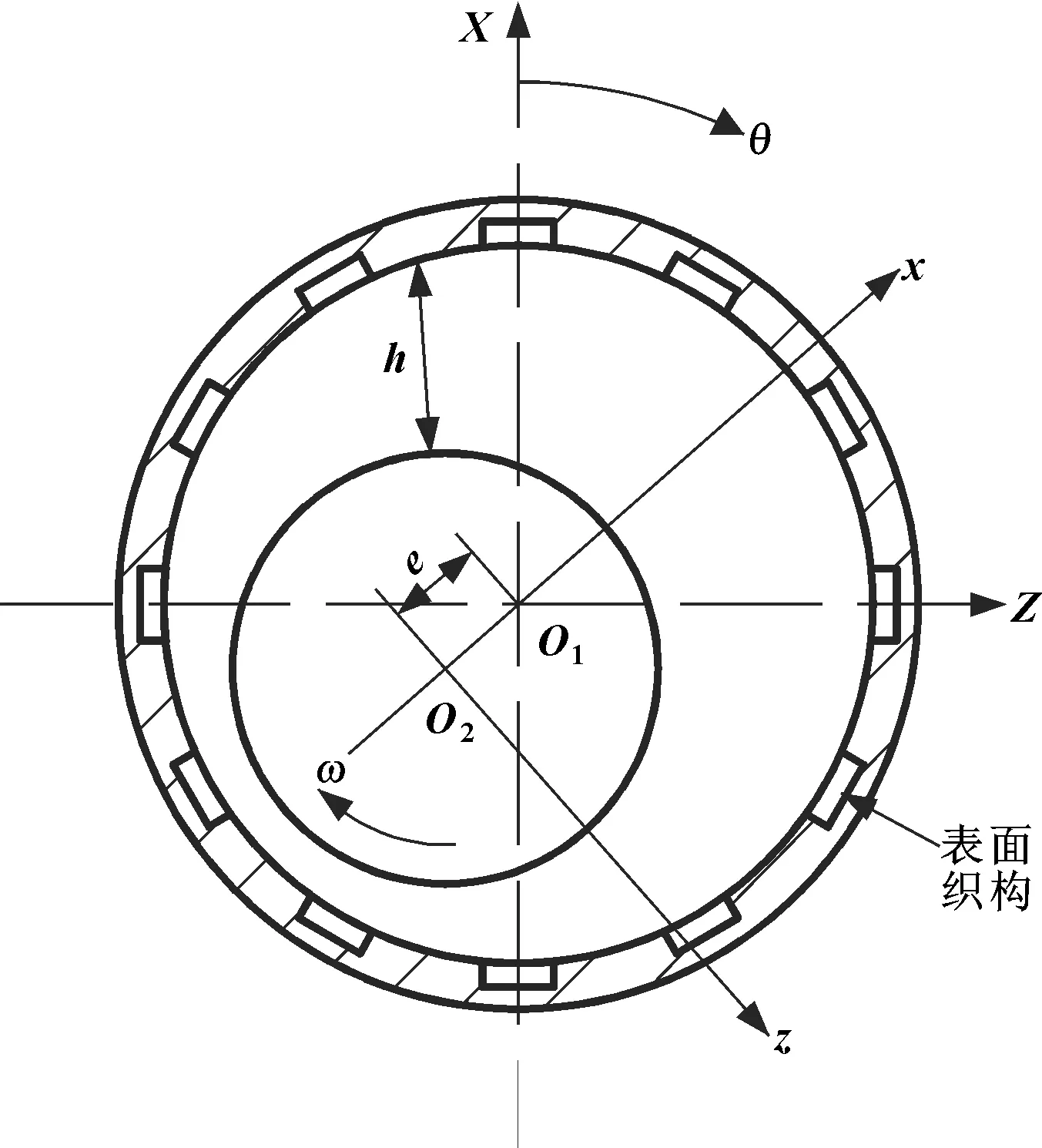
圖1 水潤滑軸承模型Fig 1 Lubrication model of water lubricated bearing

1.1 膜厚方程

如圖1所示，名義水膜厚度h的幾何近似關系為

(1)

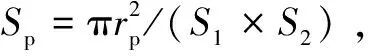
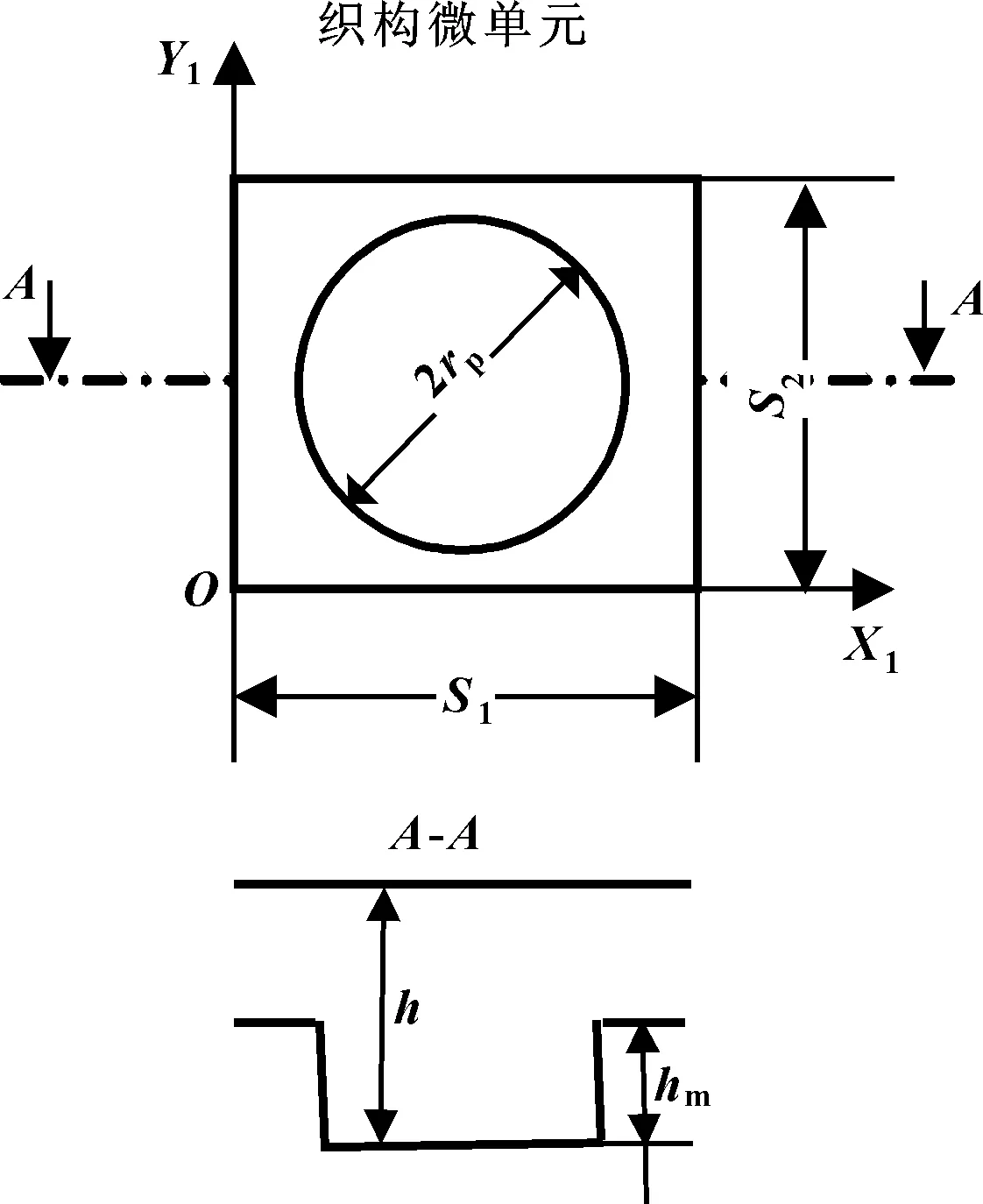
圖2 表面織構模型Fig 2 Model of surface texture

1.2 平均流量Reynolds方程

根據文獻[6],通過引入變量φ和開關函數F將水膜區和空化區的平均Reynolds方程統一起來，在數值計算過程中自動確定水膜破裂和再形成邊界。不同區域內φ的物理含義不同：

(1)在水膜完整區，φ代表量綱一壓力，即

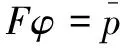
(2)

(2)在水膜破裂區，φ代表空化指數，即

(3)

其中ρ在全膜區時恒等于水的密度ρc，而在空化區時為液-汽兩相流的密度。

式(2)、(3)中，F開關函數的定義為

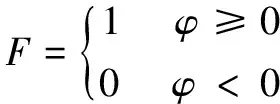
(4)

軸承量綱一化參數如下：

因此，基于JFO空化邊界條件并考慮粗糙度影響的平均Reynolds方程量綱一化形式為

(5)

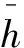
1.3 空化條件和邊界條件

JFO空化邊界條件為

在水膜的再形成邊界上：

求解壓力時的邊界條件如下：

(6)

式中：p0為環境壓力。

1.4 接觸模型

軸承表面微凸體在潤滑過程中的接觸能承擔部分載荷，根據BOWDEN和TABOR理論[9]，其接觸壓力pA計算公式為

(7)

式中：H為軸承材料的硬度。

1.5 承載力和摩擦力的計算公式

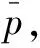
水潤滑軸承總的承載力大小為水膜承載力WH與接觸力WA之和，即

W=WH+WA

(8)

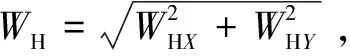
(9)

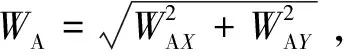
(10)

軸承總的承載力與外部負載平衡，平衡條件為

Fload+W=0

(11)

在混合潤滑狀態下，摩擦力由流體摩擦力FH和峰元摩擦力FA兩項組成，即：

(12)

式中：μf為粗糙峰接觸摩擦因數。

因此，摩擦副間摩擦因數為

(13)

2 計算結果與分析

為驗證織構模型的正確性，現暫忽略粗糙峰的接觸和JFO空化邊界條件，將計算結果與文獻[10]中的計算結果進行對比。由圖3可知，文中計算結果與文獻[10]中能夠很好地吻合，驗證了文中織構模型的正確性。下面將基于該模型及求解方法，研究不同織構深徑比及面密度對海水潤滑軸承性能的影響。

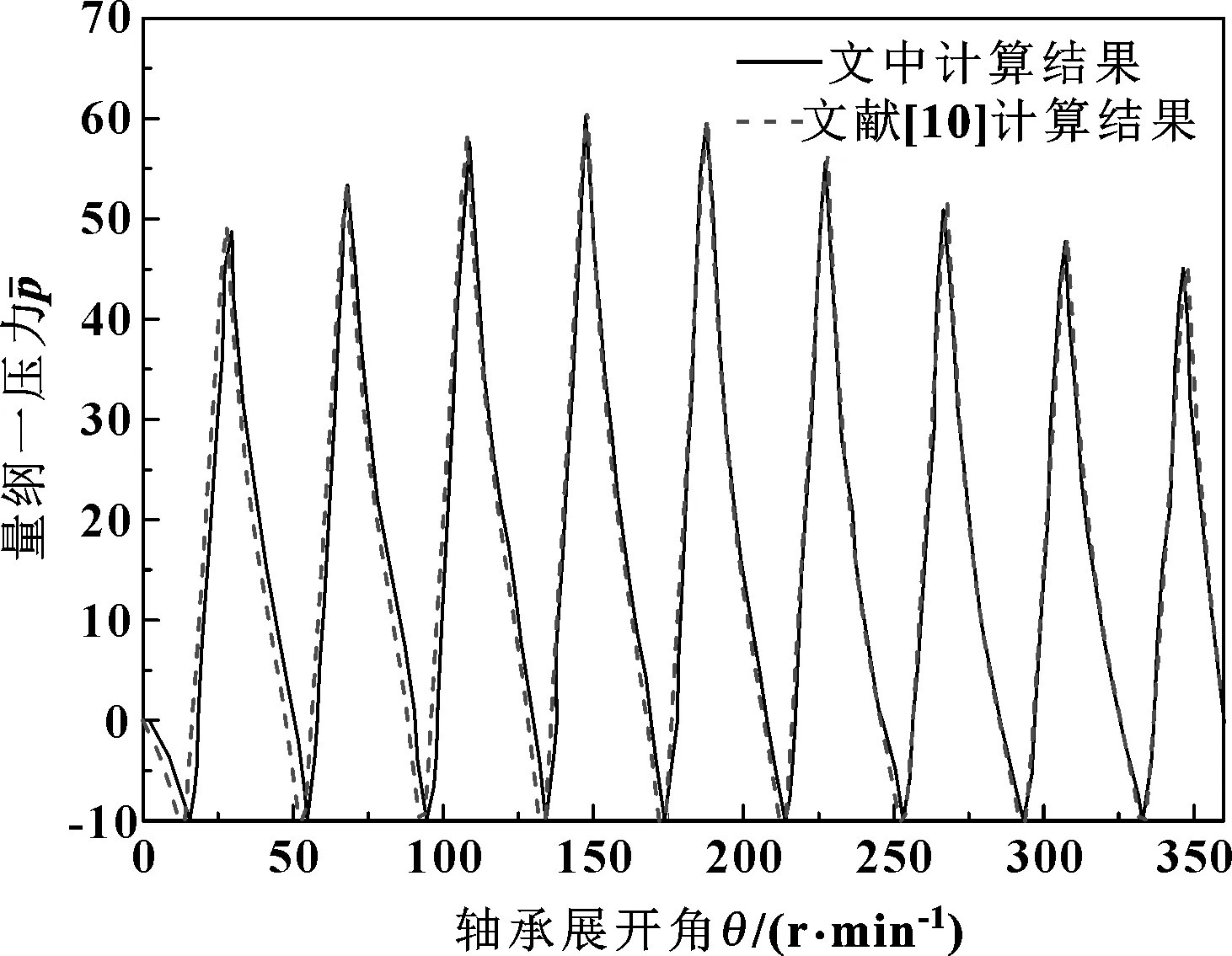
圖3 計算結果與文獻[10]對比Fig 3 Comparison of calculation results with Ref. [10]

表1給出了計算中所使用的海水潤滑軸承參數。

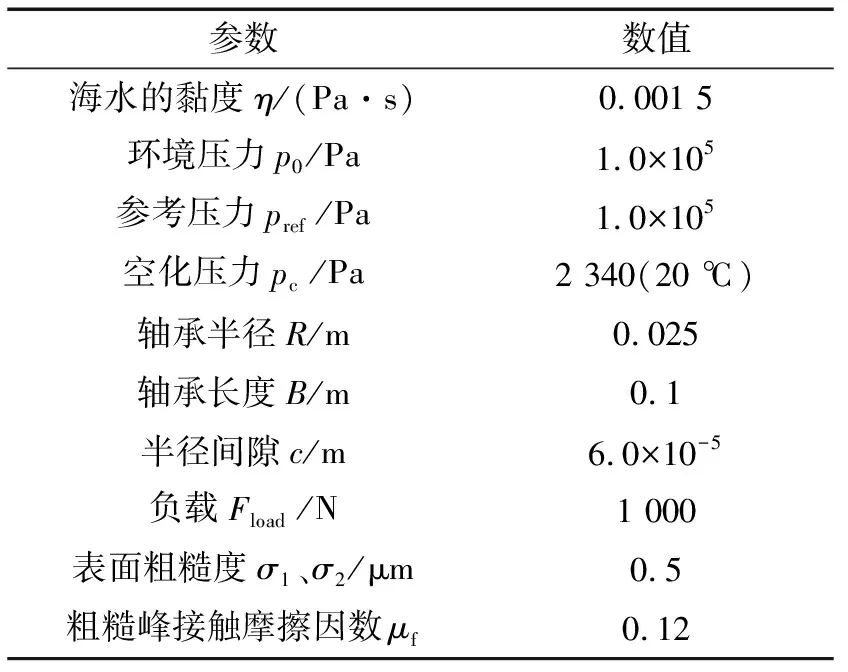
表1 海水潤滑軸承參數

2.1 織構深徑比對水潤滑軸承潤滑性能的影響

圖4所示為織構半徑rp=500 μm時，不同深徑比下最小膜厚比隨轉速的變化曲線。圖中h/σ=3的橫線代表混合潤滑和流體動壓潤滑的分界線，橫線上方代表流體動壓潤滑，下方代表混合潤滑。A、B、C、D 4點分別代表各曲線由混合潤滑進入流體動壓潤滑的轉折點。從圖4可以看出，當轉速相同而織構深徑比λ<3%時，軸承間的最小膜厚比隨深徑比的增加而增大，而當深徑比λ=3%時，軸承最小膜厚比無織構時還有所降低。

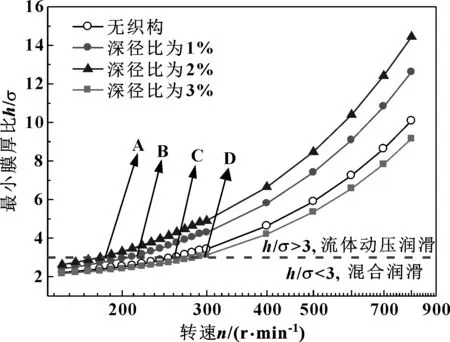
圖4 織構深徑比對最小膜厚比的影響Fig 4 Effect of texture aspect ratio on minimum film thickness ratio

圖5所示為織構半徑rp=500 μm時，不同深徑比下摩擦因數隨轉速的變化曲線。可以看出，當轉速相同而深徑比λ<3%時，摩擦因數隨深徑比的增加，呈現減小的趨勢，深徑比λ=2%時摩擦因數最小，并且在最低轉速下由混合潤滑進入流體動壓潤滑；但深徑比λ=3%時軸承摩擦因數比無織構時還有所增加，且在較高的轉速下才能進入流體動壓潤滑狀態。其原因在于：隨著深徑比的增大，織構內流體動壓效應增強，水膜厚度變大，摩擦因數減小；當深徑比過大時，由于微凹坑織構內負壓的增大，降低了流體動壓效應，反而造成了摩擦因數的增加。

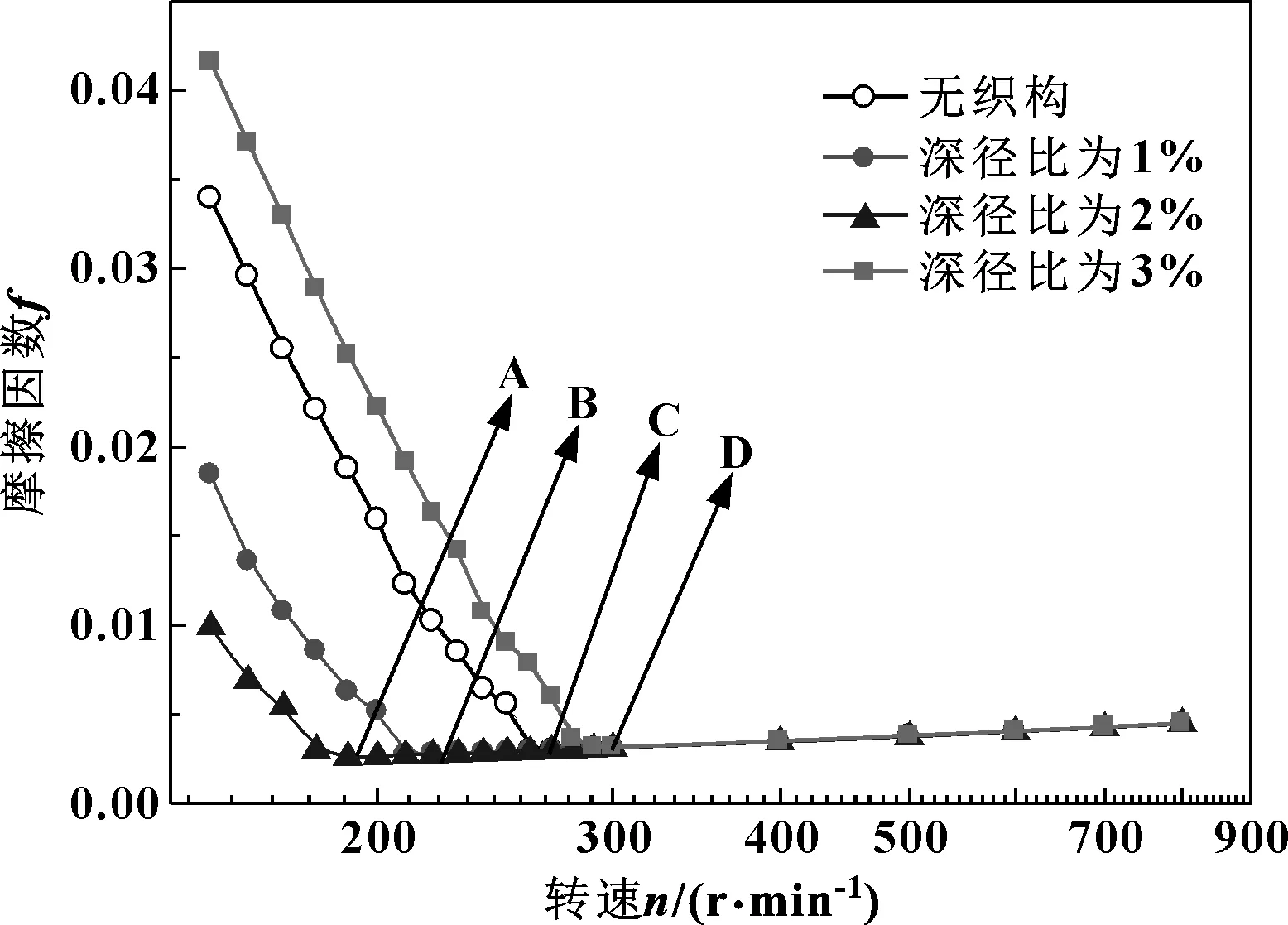
圖5 織構深徑比對摩擦因數的影響Fig 5 Influence of the ratio of depth to diameter of surface texture on friction coefficient

由此得出：織構深徑比是影響水潤滑軸承摩擦因數的重要參數之一，深徑比在一定范圍內能有效降低摩擦因數，增加水膜厚度，使軸承在降低轉速下進入流體動壓潤滑。

2.2 織構面密度對水潤滑軸承潤滑性能的影響

圖6所示為織構深度hp=10 μm時，不同面密度下最小膜厚比隨轉速的變化曲線。圖中h/σ=3的橫線代表混合潤滑和流體動壓潤滑的分界線，橫線上方代表流體動壓潤滑，下方代表混合潤滑。A、B、C、D 4點分別代表各曲線由混合潤滑進入流體動壓潤滑的轉折點。從圖6可以看出，在轉速相同而面密度Sp<15%時，軸承間的最小膜厚比隨著面密度的增加而增大，而當面密度Sp=15%時，軸承最小膜厚比無織構時還有所降低。

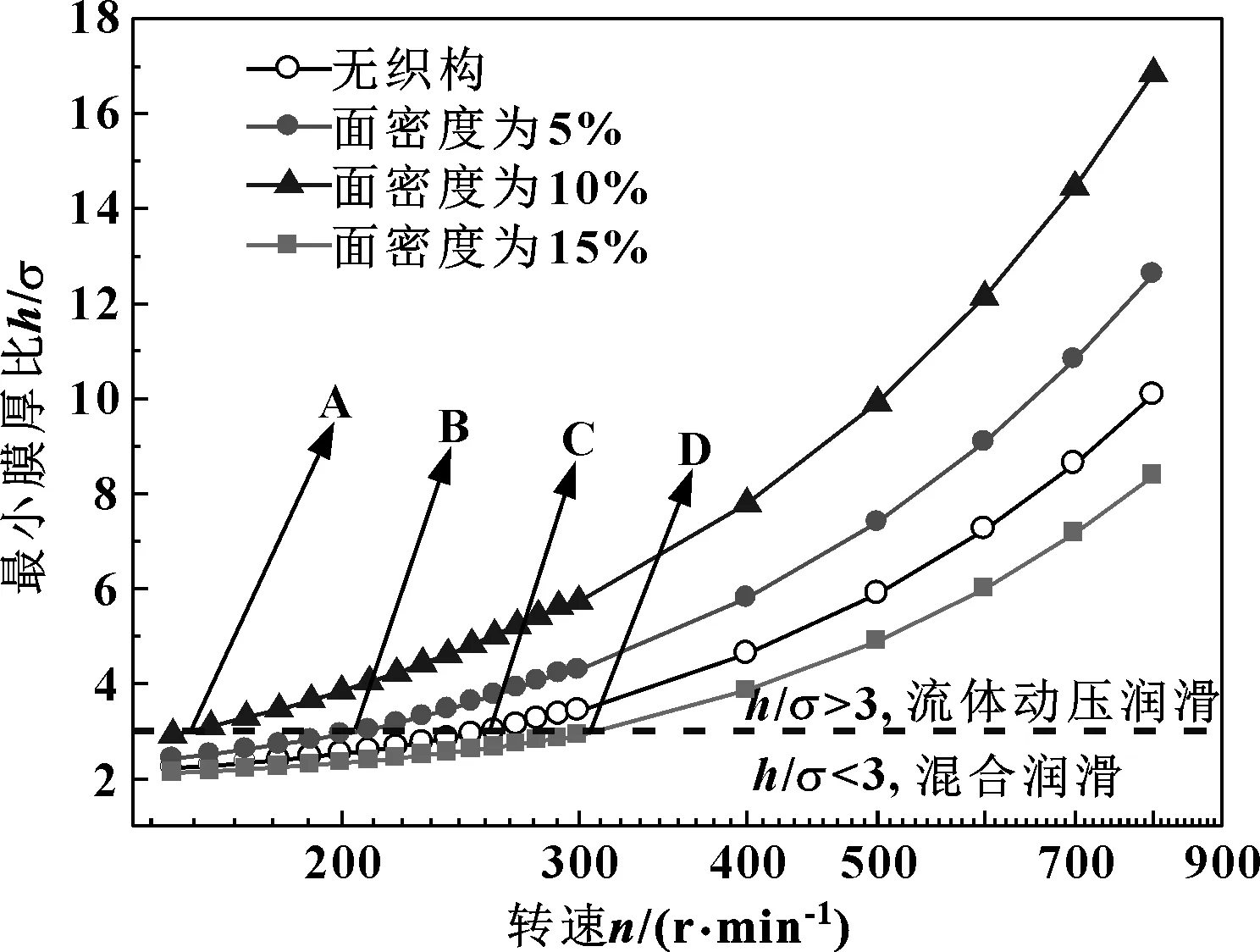
圖6 織構面密度對最小膜厚的影響Fig 6 Effect of texture surface density on minimum film thickness ratio

圖7所示為織構深度hp=10 μm時，不同面密度下摩擦因數隨轉速的變化曲線。

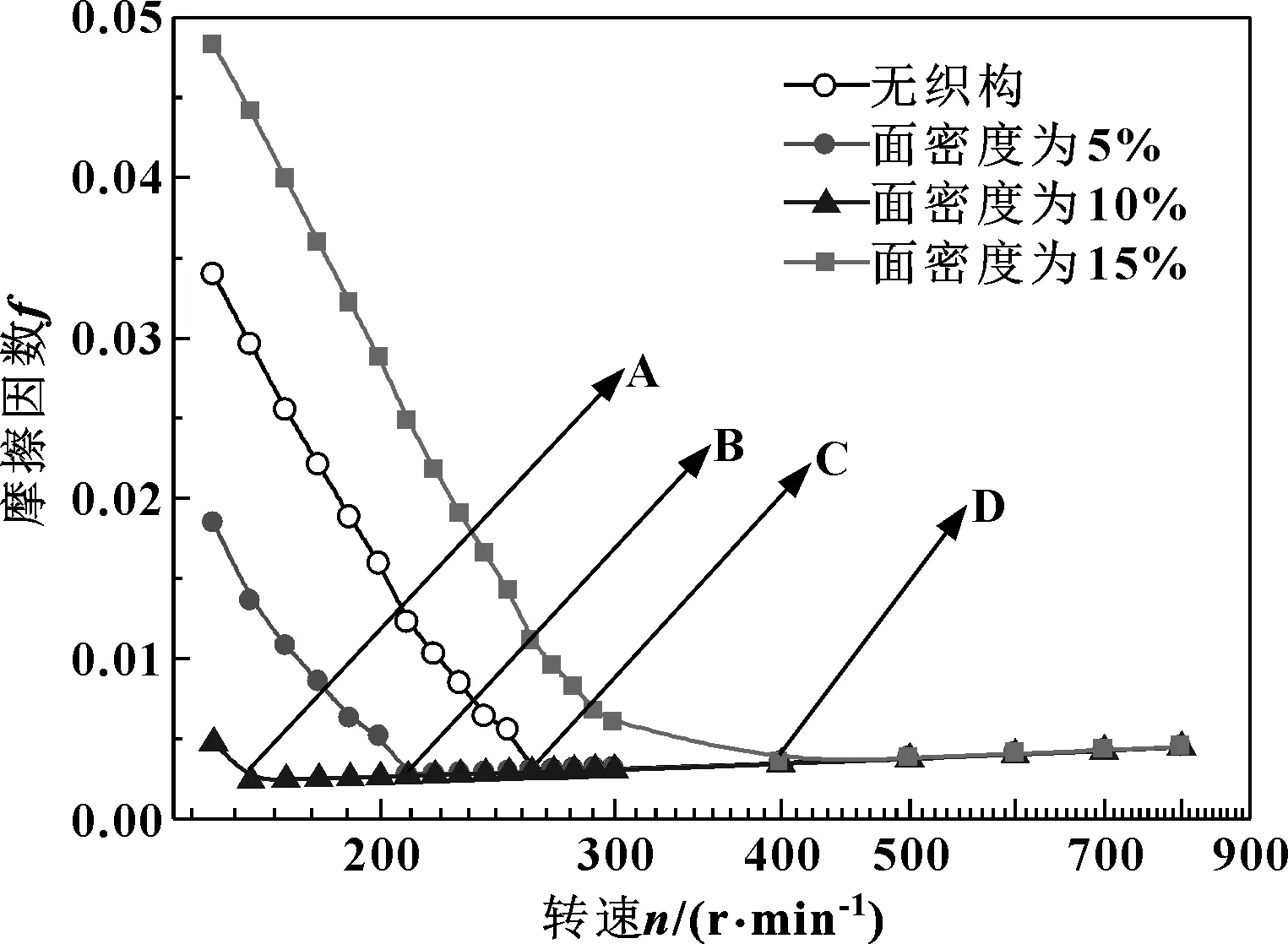
圖7 織構面密度對摩擦因數的影響Fig 7 Influence of texture surface density on friction coefficient

可以得出，當轉速相同而面密度Sp<15%時，摩擦因數隨面密度的增加，呈現減小的趨勢，面密度Sp=10%時摩擦因數最小，并且在最低轉速下由混合潤滑進入流體動壓潤滑；但面密度Sp=15%時軸承摩擦因數比無織構時還有所增加，且在較高的轉速下才能進入流體動壓潤滑狀態。其原因在于：隨著織構面密度的增大，織構內收斂楔形間隙產生的流體動壓效應升高，造成了水膜厚度的增加和摩擦因數的減小；但過大的間距會使壓力峰值降低，減弱流體動壓效應，從而造成水膜厚度的減小和摩擦因數的增大。

由此得出：織構面密度是影響水潤滑軸承摩擦因數的另一重要參數，面密度在一定范圍內能有效降低摩擦因數，增加水膜厚度，使軸承在降低轉速下進入流體動壓潤滑。

3 結論

建立帶有表面織構的水潤滑軸承混合潤滑模型，并采用JFO空化邊界條件進行數值求解，繪制了不同織構參數下軸承的Stribeck曲線，得出如下結論：

(1)表面織構的深徑比和面密度是影響水潤滑軸承摩擦因數及改善潤滑性能的重要參數，但是織構的加入并不一定能減小摩擦因數。

(2)表面織構的面密度和深徑比存在最優值，能使水潤滑軸承獲得最大的膜厚比與最小的摩擦因數，并在較低的轉速下由混合潤滑狀態進入流體動壓潤滑狀態。