基于實測數據的風電綜合負荷建模

季文偉，張偉玲（.武警海警總隊北海海區指揮部，山東 青島 66000；.國網山東省電力公司青島市黃島區供電公司，山東 青島 66000）

0 引 言

隨著電網規模的不斷擴大，大量風力發電機組接入電網，電網的復雜度越來越高，電網的動態穩定性和電壓穩定性問題更加突出，使得負荷模型對電力系統的影響不容忽視。廣域測量系統（WAMS）中，相量測量單元（PMU）能實現對電力系統各個節點動態數據的同步采集，不僅為電力系統在線應用領域中的分析、控制功能的研究開發提供了豐富的新數據源，也為電網在線動態建模的實現提供了成熟條件。目前，風電機組模型大都由廠家給定或采用經驗值，模型參數給定值與實際值的偏離將直接影響仿真結果的可靠性。因此，有必要基于實測數據對風電機組進行參數辨識[1-5]。

本文在傳統負荷模型的基礎上建立包含風力發電的綜合負荷模型。通過對綜合負荷模型的分析，選擇總體測辨法求出模型的主要參數。在利用粒子群優化算法辨識參數的過程中，以計算的功率值與實測功率值的誤差最小構造目標函數。基于風電綜合負荷模型，以華北電網御道口220 kV節點某母線實測PMU數據為依據，辨識考慮風電綜合負荷的模型參數，以驗證辨識方法的有效性，并判斷辨識結果的合理性。

1 構建電網綜合負荷模型

綜合負荷模型是靜態負荷、配電網無功補償和動態負荷按一定比例的組合，模型結構如圖1所示。

圖1 模型結構圖

對于含風力發電系統的配電網側而言，在等值電機模型中，母線上安裝大量雙饋感應風力發電機（WG），使得圖1中WG向母線輸出的有功功率PWG與輸入到電動機負荷中的有功功率PIM方向相反。

采用電動機慣例的異步發電機和異步電動機，在數學描述上有相同的形式。將異步發電機和異步電動機等效為統一異步電機，在計算中電機采用三階等值電路模型[6-7]。結合電網實測數據，下文各變量均采用實際值，則動態負荷中異步電機的方程組如下：

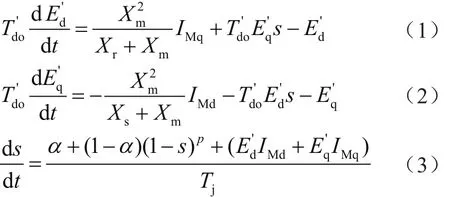
其中：

式中，s為異步電機滑差；Xr為轉子電抗；Xm為定轉子互抗；Rr為轉子電阻；Tj為轉子慣性時間常數；IMd、IMq分別為異步電機電流的d、q分量；分別為異步電機暫態電動勢的d、q分量；為異步電機定子開路時d軸轉子回路時間常數；α為與轉速無關的阻力矩系數：p為與轉速有關的阻力矩的方次。

因定子電阻Rs取典型值0 Ω，電機定子電流與電壓的關系可簡化為：

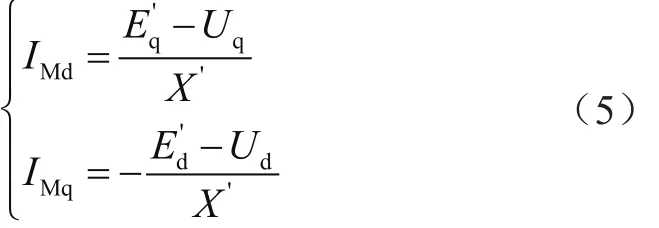
其中：

式中，Xs為定子電抗。

異步電機功率為：

式中，PM、QM分別為異步電機的有功功率與無功功率。

在綜合負荷模型中，由于靜態負荷所占比例很小，對參數辨識影響不大，所以為方便計算，本文采用恒阻抗模型表示等值靜態負荷，其有功功率PS與無功功率QS為：

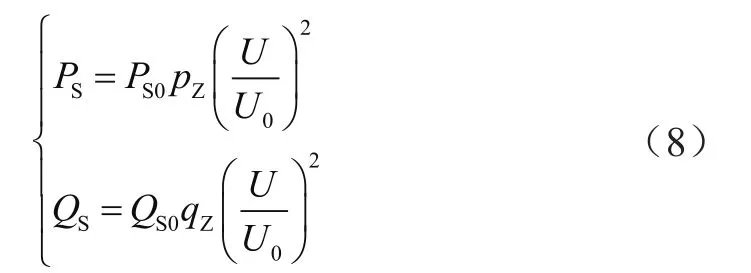
式中，PS0和QS0分別為系統穩態運行下的有功初始值和無功初始值；pZ為對應恒阻抗的有功功率系數；qZ為對應恒阻抗的無功功率系數；U、U0分別為電壓實際值與初始值。

異步電機有功功率所占總用功功率的比例PMP為：

2 電網綜合負荷參數辨識研究

在已知負荷母線初始電壓U0、負荷母線上的總功率P0及其他參數的情況下，部分初始化過程如下。

電機初始有功負荷為：

根據文獻[8]可知，異步電動機負荷率系數為：

在確立異步電機動態負荷模型后，由式（5）求解出定子電流IMd、IMq，其中Ud、Uq用實測Udm、Uqm代入。根據當前時刻狀態變量s與定子電流IMd、IMq，利用改進Eluer法求解異步電機微分方程組，得到下一時刻的狀態變量這樣可以從初始時刻開始計算實測數據記錄長度內每一時刻點的IMd、IMq，進而求得PM、QM。

節點的有功功率與無功功率計算公式為：

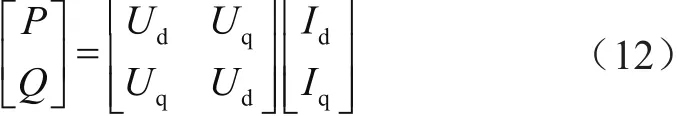
其中，I為動態模型電流IM和靜態模型電流IS之和，Id、Iq分別為I的交、直軸分量。

將節點電壓作為已知量輸入，將電流作為輸出量，通過狀態變量與式（8）計算功率值，與實測功率值進行比較，以二者的誤差最小作為目標函數，辨識綜合負荷模型的參數。

負荷模型優化目標函數[9-10]為：

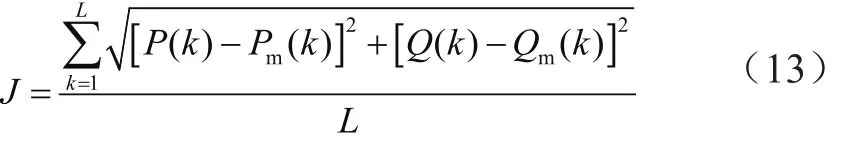
式中，k表示離散采樣時刻；L為實測數據記錄長度；P(k)和Q(k)分別表示實測有功和無功曲線k時刻的輸出向量值；Pm(k)和Qm(k)分別表示模型計算的有功和無功曲線k時刻的輸出向量值。根據式（13）的目標函數，采用粒子群算法（PSO）對模型進行參數辨識。

表1 參數辨識結果

3 實測算例參數辨識驗證

華北電網御道口/御祥線220 kV母線下是以大量風力發電機組為負荷中心的電網。以2014年4月某天內5個不同時段的實測PMU數據為例，進行參數辨識算例的驗證，辨識結果如表1所示。由靈敏度分析，重點辨識參數的初始搜索范圍為：Xs取558.8～1 005.84 Ω，接近典型值；s0取-0.08～0，因為該母線下包含大量的風力發電機，初始滑差應為負；PMP取1～8，因為對于風力發電系統而言，該母線上安裝了大量雙饋異步風力發電機，而所接靜態負荷與輸入有功功率絕對值相對較小，使得PMP略大于1；Tj取1～3；其他參數則取典型值Rs=0 Ω、Xr=670.561 3 Ω、Rr=111.760 0 Ω、Xm=19 558 Ω、P=2、α=0.15、PZ=1、QZ=1。其中，電壓的基準值為220 kV，功率基值為15 MVA。在粒子群算法尋優的過程中，設定種群規模為20，進化次數300次。

由電壓和電流可以求解有功功率和無功功率在各個時段的計算值。為分析方便，取殘差最小的兩組數據得到有功功率和無功功率的擬合曲線，分別如圖2和圖3所示。

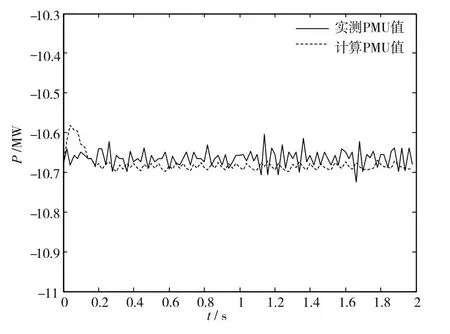
圖2 有功功率擬合曲線

圖3 無功功率擬合曲線

表1給出了滿足要求的5組實測PMU數據的參數辨識結果。可以看出，定子電抗的辨識范圍為632.002 8～770.026 4 Ω，轉子初始滑差辨識范圍為-0.065 8～-0.031 9，電動機比例系數辨識范圍為1.002 3～1.102 5，轉子慣性時間常數辨識范圍為1.903 6～2.074 8。殘差范圍0.000 5～0.002 3，辨識結果比較平穩，說明辨識方法有效，結果合理。

從圖2和圖3的辨識結果可以看出，有功功率和無功功率吻合稍有誤差。采用具有全系統統一時標的數據進行區域負荷辨識，主要是因為節點綜合負荷模型的負荷和參數本身具有時變性，辨識理論要求辨識起始點是平衡點，而實際運行系統隨機擾動時時存在，很難找到平衡點。但是，這個誤差對參數辨識結果幾乎沒有影響，PMU實測數據在風電綜合負荷建模中得到了很好應用，進一步驗證了所選方案的合理性。

4 結 論

基于實測數據的風電綜合負荷建模，是將負荷母線下的異步風力發電機和異步電動機等效為統一異步電機，并建立綜合負荷模型。采用粒子群優化算法，以計算功率值和實測的功率值二者誤差最小作為目標函數，對綜合負荷模型最優化問題進行求解，并利用實測PMU數據驗證了該模型的有效性，最終辨識出Xs、s0、PMP和Tj共4個參數。其中，轉子初始滑差s0小于0，電動機負荷比例PMP略大于1，充分說明含有大量風力發電機負荷模型的特點，且根據功率計算值與實測值擬合曲線效果較好，驗證了該負荷模型，并為該綜合區域電網負荷模型的網絡參數可辨識性做出了合理化分析。