電動汽車無序充電的影響分析

郝 越

（深圳供電局有限公司，廣東 深圳 518000）

0 引 言

隨著技術的進步，電動汽車的數量正在不斷增加[1]。同時，電動汽車作為移動式儲能裝置，在削峰填谷、提供電力系統輔助服務、協同消納新能源等方面具有廣闊的應用前景[2]。但是，電動汽車的無序充電可能會導致電網的峰谷差加劇、電壓下降等不利影響，因此對電動汽車無序充電的過程進行分析尤為重要[3]。

由于電動汽車的型號和種類多樣，主要分為交流1級、交流2級和直流充電電動汽車，其充電功率存在較大差別[4]。電動汽車的數量和充電功率對電網的影響不同，因此分析不同充電功率等級的比例，既能滿足用戶的需求在充電連接時長內獲取預期的充電電量，也能減少設備投資，降低電動汽車無序充電負荷的峰谷差[5]。

為進一步優化電動汽車的充放電過程，文獻[6]提出基于粒子群算法的電動汽車充電策略研究，以電動汽車電費最小為目標的充電策略，沒有考慮電動汽車的充電功率影響；文獻[7]針對電動汽車有序充電提出了原對偶內點動態優化算法，實現了以網損最低為目標的電動汽車充電模型求解，具有計算速度快、收斂性好的特點；文獻[8]以充電功率為特征參量，研究了考慮充電樁利用率、充電等候時間、充電樁占地面積等因素的電動汽車充電樁優化設置，使得使用充電樁的社會成本最低。目前，以電動汽車的充電功率為目標的充電策略成果較少。

為此，本文以電動汽車充電功率為研究對象，采用多項式擬合的方法獲得電動汽車充電量與時間的對應關系，從而獲得電動汽車的負荷曲線。由于已接入充電的車輛其充電時間不會在負荷峰值處疊加，負荷曲線的峰值就會減小，因此采用拉格朗日乘數法建立優化模型，求解得到不同充電功率的電動汽車的占比情況。

1 電動汽車負荷曲線模型

電動汽車的充電時段與初始接入時間和連接時長有關。對于第一個時間段，假設起始時間是t0，終止時間是t1。為了簡化分析，假設在這一個時間段內接入充電的車輛均在t0時刻接入。接入的車輛中，交流1級、交流2級、直流充電分別占比a、b、c，且a+b+c=1。各類型汽車的充電功率均按照給定功率范圍的中間值計算。

由此，t0時刻接入充電的汽車總功率為：

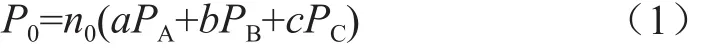
式中，P0為t0時刻接入充電的汽車總功率，n0為該時刻接入充電的汽車臺數，PA、PB、PC分別為交流1型、交流2型、直流型汽車的充電功率。

在得到t0時刻接入充電的汽車總功率P0后，可以計算該時刻接入的汽車所需要的充電時長：

式中，h0為t0時刻接入充電的汽車所需的充電時長，Q0為該時刻接入的汽車所需的充電電量。同樣地，可以得到第二個時間段，即t1時刻接入充電汽車的總功率P1和充電時長h1。

在獲得第一個時間段和第二個時間接入充電的汽車分別需要的充電時長h0、h1后，比較t0、t0+h0、t1、t1+h1的關系，即可得到第一個時間段和第二個時間段的負荷分布情況：當t0+h0＜t1時，則第一個時間段內的負荷功率為P0，第二個時間段的負荷功率為P1；當t1＜t0+h0＜t2時，則第一個時間段內的負荷功率為P0；第二個時間段內，t1～t0+h0時段的負荷功率為P0+P1，t0+h0～t2時段的負荷功率為P1，由于劃分的時間段較小，可以在具體求解過程中粗略認為第二個時間段及t1～t2時段的負荷功率都為P0+P1。

上述過程僅考慮了兩個時間段的情況，事實上對任意一時間段進行負荷分析時，均需要考慮前面所有時間段對該時間段的影響。

對于第n個時間段，假設前m（m＜n）個時間段內接入充電車輛均對該時間段有影響，即在tn-m-1、tn-m…tn-2時刻接入充電的電動汽車，再加上其充電時間hn-m-1、hn-m…hn-2后，均大于tn-1。此時，第n個時間段的負荷功率為Pn-m-1+Pn-m+…+Pn-1，如圖1（a）所示。

若中間某一個時間段內接入充電車輛均對該時間段未對該時間段造成影響，則可剔除該時時間段內接入充電車輛的充電功率。例如，若前k個時間段未對第n個時間段造成影響，則第n個時段負荷功率為Pn-m-1+Pn-m+…+Pn-k-2+Pn-k…+Pn-1，如圖 1（b）所示。

在上述模型中，對任意一個時間段i均有兩個量是未知的，即每個時刻接入的汽車所需的充電電量Qi，每個時刻接入充電的汽車數量為ni，故需要確定Qi與ni。

（1）ni的確定。在已經得到了每個時刻接入充電的車輛數與時間的概率分布情況后，即得到了n隨t的概率密度曲線法f1(t)，利用f1(t)可以求出車輛在第i個時間段內充電的概率：

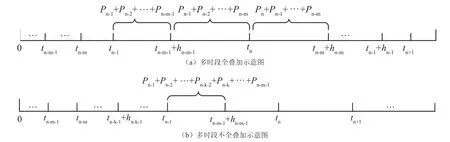
圖1 多時段疊加示意圖

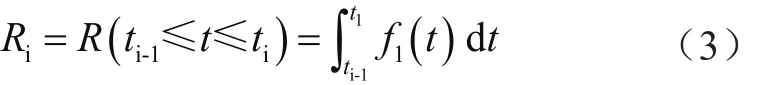
式中，Ri表示汽車在第i個時間段內充電的概率，N為汽車總數，且ni=NRi。

（2）Qi的確定。同n一樣，若能獲取Q隨時間的分布特性，則可以較容易獲得各個時刻接入充電的汽車所需的充電量，故需利用已知數據構造出Q與時間的分布關系。在已知數據中，分時段統計該時段內接入充電的汽車臺數與充電量，若在第i個時間段內統計得到的汽車臺數為m臺，相對應充電量分別為Qi,1，Qi,2…Qi,m，則可以求出：

式中，為該時間段接入充電的汽車的充電量的均值，用以模擬該時間段所有接入充電的汽車的充電電量。

在獲取所有時間段的充電電量均值后，即可利用均值擬合出充電電量與時間的關系曲線fQ(t)。雖然是用各個統計時間段內的均值模擬的充電電量與時間的關系，但是均值可以充分反映樣本總體的數值大小。此處需要求解總體的負荷特性，而非單個電動車的負荷特性，所以是合適的。

獲得充電電量與時間的關系曲線fQ(t)后，即可獲得任意一時刻電動車的充電電量。由于調度時通常是每過一個時間段（通常為15 min），即對電網的運行狀態進行依次評估，所以關注的往往也是該時間段所需用電量的均值，即：

通過式（5），即可獲得每個時間段接入的汽車所需的充電電量Qi。

2 充電功率等級比例優化模型

在保證用戶需求的前提下，通過改變不同類型充電功率等級的比例，可以有效降低電動汽車無需充電負荷的峰谷差，改善電力系統的運行狀況。但是，隨著不同充電功率設備比值的變化，充電站的投資必然有所改變。需要尋找合適的比例，使峰谷差降低的同時，充電站的投資并不出現劇烈的增加。

通過分析可以發現，負荷隨時間的分布與電動汽車接入量隨時間的分布具有強烈的相關性，所以負荷的峰谷也出現在電動汽車接入量的峰谷處。本文模型是使用時間段的疊加量來表征負荷功率的大小，如果保證在負荷峰值周圍的時間段都不疊加，即可減小峰值處的負荷功率。根據這個思路建立相應的優化模型。

設α、β、η分別為交流Ⅰ型、交流Ⅱ型、直流型充電設備負荷所占比例，為了使峰值處不產生充電時間的重疊，則：

假設交流Ⅰ型、交流Ⅱ型、直流型充電設備每臺的成本為C1、C2、C3，則總的建設成本為：

式中，M為充電樁總數。由于總數一定，M的大小只會導致制造成本成比例增加，極值點所在位置的α、β、η值不會改變，所以可以建設成本中去掉M，對求解極值點的α、β、η值不會造成影響，則建設成本的表達式可以簡化為：

在式（6）中，等號左邊所得值越小，則高功率設備所占比例越大，建設成本也就越高。為達到減少建設成本且降低峰谷差的目的，所以將該式的值取1，即：

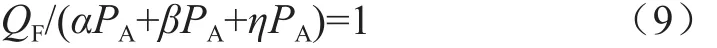
式（9）為式（8）的一個約束條件。對式（8）求極值，可以建立一個基于拉格朗日乘數法的模型：

對式（10）求偏微分，且令偏微分結果為0，即：

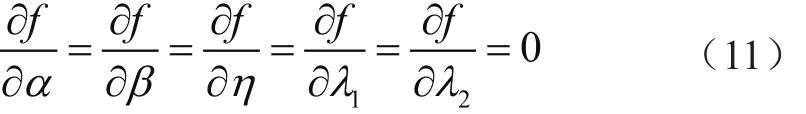
求解方程組，即可得到合適的α、β、η。

3 算例分析

電動汽車的功率主要分3個等級，相關參數如表1所示。選取1 h作為時間間隔，對電動汽車的充電電量與時間關系進行統計分析。數據選用2018屆電工數學建模A題附錄1中的數據。

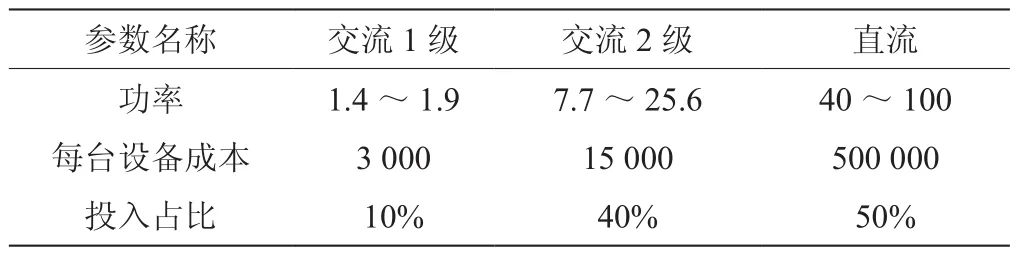
表1 不同功率電動汽車的相關數據

采用多項擬合的方法，得到充電電量隨充電時間的變化曲線如圖2所示，函數表達式為：

其 中，fQ(t)為汽車充電電量，p1=-6.43e-7，p2=0.002 1，p3=-0.035，p4=0.28，p5=-0.95，p6=0.087。

圖2 電動汽車充電量與時間的關系

由圖2可看出，在夜間0:00-5:00、18:00-24:00時段內，電動汽車不行駛，可以長時間充電，此時段內電動汽車的充電量較大。白天時段內車主要用車，電動汽車不能長時間連接充電樁，此時段內充電量較小，充電量在此時段內隨時間平穩波動。

利用得到的充電電量隨充時間變化的函數表達式，計算出每個時刻的充電電量Q，同時利用充電車輛數隨時間變化的概率密度曲線，計算各個時刻接入充電的汽車數量n，結合模型，即可求解各個時間段的負荷功率，具體數據見表1，負荷隨時間的變化曲線如圖3所示。

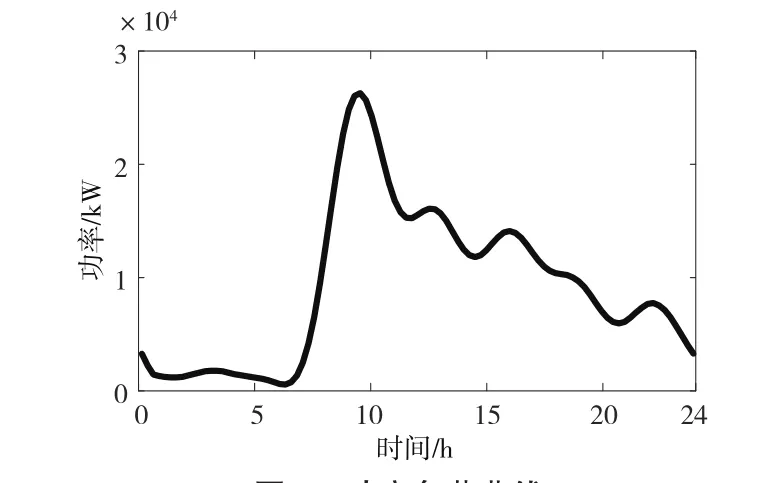
圖3 功率負荷曲線

從圖3可以清楚看出一日內負荷功率的變化情況。從0:00-6:00，負荷一直處于低位運行，其中0:00-1:00呈現下降趨勢。結合電動汽車的運行特征分析可以發現，在0:00-6:00這個時間段內，接入充電的電動汽車數量很少，即使每一臺接入充電的汽車的充電電量最大，總的充電功率依然很小。而導致0:00-1:00呈現下降趨勢的原因主要包括兩方面：一是接入充電的車輛數減少，二是前一天接入充電的車輛到這個時間段基本上都已經充到了理想的充電電量，不再對這一時間段的功率造成影響。6:00-10:00負荷功率陡增，這個時間段電動汽車行為變得活躍，人們上班等活動均導致電動汽車自身的用電量減少，電動汽車需要沖電的傾向顯著。所以，這一時間段接入充電的車輛數明顯增加，即使每臺車的充電電量不是很大，負荷功率依然會出現明顯的上升趨勢。每個時刻接入充電的車輛相互疊加影響，導致負荷功率上升的趨勢十分明顯。10:00以后，負荷功率呈現有起伏的下降趨勢。10:00左右負荷功率到達峰值后，每個時刻接入充電的汽車數量逐漸減少，這是由于之后的時間段不會出現早上擁堵式的汽車接入，人們對電動汽車的使用也不會像早上上班這樣密集。在明顯的活躍期，如12:00、14:00-15:00、17:00以及21:00等汽車活動的活躍時段，又呈現出上升趨勢。此外，晚高峰也是電動汽車使用的高峰期，但是在從當日晚高峰后到第二天早高峰前比較寬裕的時間段進行充電，負荷不會出現陡增的現象。此外，負荷功率和電動汽車接入數量有著類似的分布。

電動汽車為1萬輛時，其負荷峰值為25 764 kW·h；當電動汽車數目為 307時，QF為83.92 kW·h。PA、PB、PC采用中間取值的方法，通過拉格朗日乘數法可計算得到交流1型、交流2型、直流型充電設備負荷所占比例分別為α=0.312、β=0.627、η=0.063。

4 結 論

在無法直接求得充電功率的情況下，本文利用充電電量求取各個時刻接入充電的車輛所需的充電時間，利用充電時間的疊加間接求出充電功率，獲得負荷曲線。結果表明，在10:00時電動汽車的充電負荷最高。考慮到前面時刻接入充電的車輛的充電時間不會在負荷峰值處疊加，負荷曲線的峰值會減小，利用拉格朗日乘數法建立優化模型，求得3種功率充電設備的占比分別為0.312、0.627、0.063。