非均勻加熱管內超臨界CO2傳熱特性研究
吳家榮,李紅智,楊 玉,韓萬龍
(西安熱工研究院有限公司,陜西 西安 710054)
超臨界CO2布雷頓循環(SCO2-BC)因布局簡單靈活,循環效率高,設備緊湊,工質無毒、廉價等優勢在核電、煤電、余熱回收和艦船推進等多個領域得到了越來越多的研究[1-4]。作為SCO2-BC 發電系統的關鍵環節,超臨界CO2在鍋爐氣冷壁內的傳熱流動規律關系著整個系統的安全和效率。不同于亞臨界流體,超臨界CO2的物性隨著壓力和溫度的變化呈現強烈的非線性變化,尤其在擬臨界點附近,流體的比定壓熱容和導熱系數會發生明顯突變,如圖1所示。物性變化及其引起的自然對流使流動狀態由單一的強制對流發展為復雜的混合對流,伴隨而來的是傳熱惡化和強化的發生,這給鍋爐氣冷壁的熱力設計造成了困難。
目前,比定壓熱容和導熱系數的增大被認為是傳熱強化的主要原因;而關于傳熱惡化,一種觀點是Ackerman 等人[5]根據超臨界水傳熱提出的擬膜態沸騰理論,另一種則是Jackson 等人[6-8]提出的傳熱惡化與浮力效應和加速效應對湍流的產生和傳熱有關。
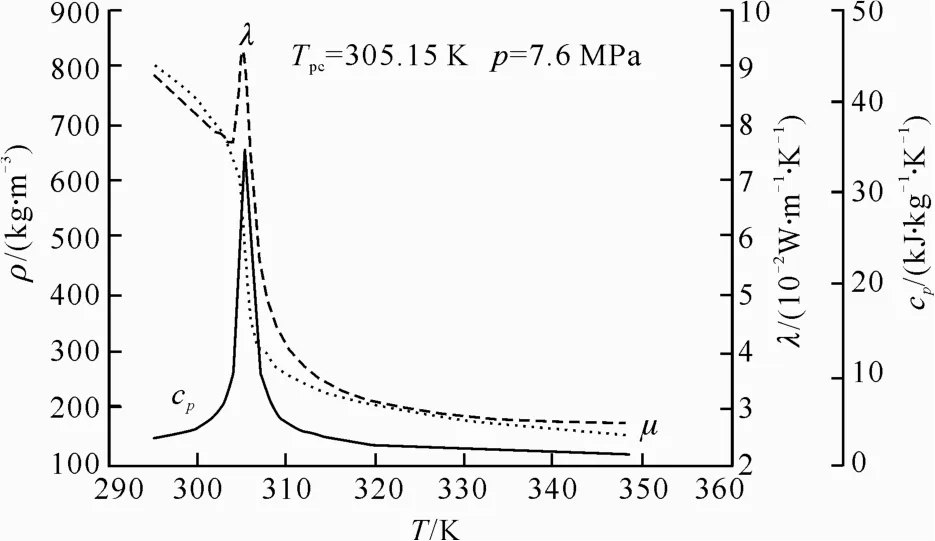
圖1 CO2 物性Fig.1 Physical properties of CO2
針對上述觀點,各國學者開展了大量超臨界流體的傳熱研究。但是,這些研究[9-12]絕大多數都是在均勻熱流條件下開展的,這與氣冷壁在爐膛內單側受熱的實際情況不符。因此,也有學者開始重點研究超臨界流體在非均勻熱流條件下的流動傳熱。Bai 等人[13]比較了超臨界水在均勻和非均勻加熱圓管內不同母線處的壁溫、溫差、對流傳熱系數隨主流焓的變化,模擬結果表明,非均勻加熱時,圓管周向壁溫的分布是不均勻的,傳熱強化也僅發生在局部區域,某些母線處甚至出現流體溫度高于壁溫的情況。Fan 等人[14]利用數值模擬對高質量流速下超臨界CO2在豎直非均勻加熱圓管中的傳熱特性進行了研究,結果表明,熱流密度很大的頂部母線處浮力和加速效應對傳熱的影響遠大于熱流密度較小的底部母線處。強化傳熱的主要原因是擬臨界區比定壓熱容的增大;而傳熱惡化除受浮力和加速效應的影響外,還源于管內黏性底層的增厚。Gu 等人[15]比較了超臨界水在內螺紋管內均勻和非均勻受熱的情況,數值模擬結果顯示,非均勻受熱時,因管內旋流的影響,流體混合更好,使得管內最高內壁溫比均勻受熱時的最高內壁溫低了10 K,且最高內壁溫并不總出現在受熱面的中點。上述對超臨界流體在非均勻熱流條件下的研究都集中在內徑> 10 mm、質量流量較大的情況,對小管徑情況下超臨界CO2傳熱特性的研究還存在不足。
綜上所述,本文開展了超臨界CO2在非均勻熱流密度下圓管內傳熱的數值模擬研究。所選取的參數為:質量流速100 kg/(m2·s)、熱流密度28~50 kW/m2、壓力7.6~8.6 MPa。通過在加熱段一側施加熱流以模擬氣冷壁受熱情況,比較了均勻和非均勻加熱的差別,分析了非均勻加熱情況下熱流密度和入口壓力對對流傳熱系數、浮力效應和加速效應的影響,總結并檢驗了4 種常用傳熱關聯式對本文數據的適用性,最后提出并檢驗了新的傳熱關聯式。
1 物理模型和控制方程
圖2為加熱圓管的幾何模型。圖中豎直圓管外徑為8 mm,內徑為5 mm,加熱段長660 mm,進出口段長110 mm。在圓管外壁的一側施加熱流,由于管壁周向和軸向導熱的存在,整個圓管的熱流密度是非均勻的。
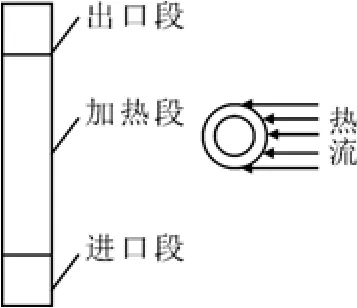
圖2 加熱圓管幾何模型Fig.2 Geometry model of the heated circular pipe
笛卡爾坐標系下可壓縮流體的連續性方程為

式中:ρ為密度,kg/m3;ui為速度分量,m/s。
動量方程為
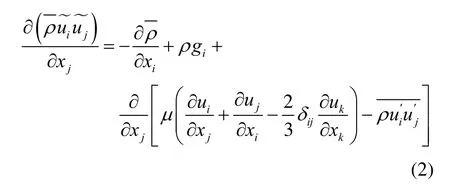
式中:gi為重力加速度分量,m/s2;為黏性系數,kg/(m·s);uj、uk為速度分量,m/s;u′為速度脈動量,m/s。
能量方程為
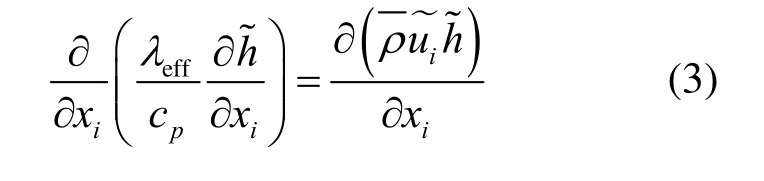
式中:λeff為有效導熱系數,W/(m·K);h為焓,J/kg;cp為比熱容,J/(kg·K)。
湍動能方程為
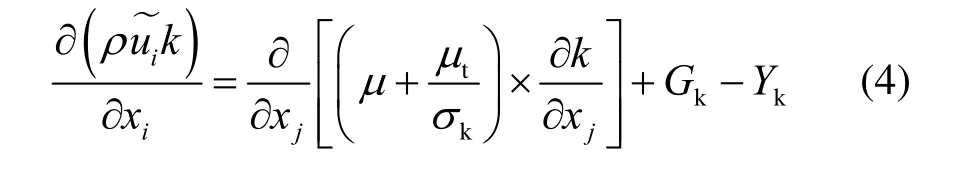
式中:μt為湍流黏性系數,kg/(m·s);k為湍動能,J/kg;σk、Gk、Yk為模型系數。
耗散率方程為
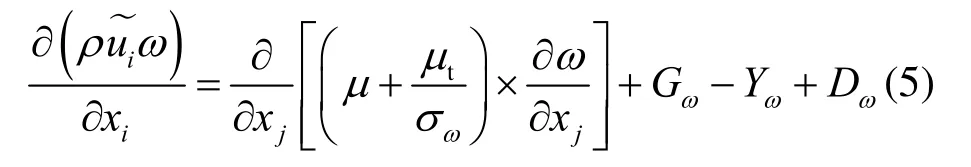
式中:ω為耗散率;σω、Gω、Yω、Dω為模型系數。
式(1)—(5)中,上標“—”表示時間平均項,上標“~”表示Favre 平均項,各項具體的表達式可參考文獻[16]。
2 邊界條件和網格無關性檢驗
在ICEM CFD軟件中劃分六面體結構網格并加密流固耦合面的網格。流體域第1 層網格高度設為0.000 2,以保證第1 層網格質心到內壁面的無量綱距離y+小于1。數值模擬借助ANSYS Fluent 軟件進行,固體域材料為316L 不銹鋼,流體域材料選取ANSYS Fluent 軟件內嵌套的NIST 真實氣體物性庫中的實際CO2,開啟Z方向的重力加速度。入口邊界條件選取可壓縮流體常用的質量入口,出口邊界條件選取壓力出口。湍流模型選取SSTk-ω兩方程模型,采用壓力速度耦合的SIMPLIC 算法,動量、能量、湍動能和耗散率方程的離散均采用二階迎風格式,松弛因子保持默認。連續性方程、動量方程、能量方程、湍動能和耗散率方程的收斂殘差設置為1.0×10-6,當殘差曲線和進出口平均溫度不發生明顯變化,且進出口質量流量的誤差小于1%時,可認為計算收斂。
選取質量流速G=100 kg/(m2·s)、熱流密度qwi=50 kW/m2、入口壓力p=7.6 MPa、入口溫度Tin=295.15 K 的工況,分別采用4 套網格計算所給幾何模型的加熱段壓降,結果見表1。

表1 網格數與加熱段壓降Tab.1 The grids number and the pressure drop of heating section
由表1可知,加熱段壓降隨網格數量增大而增大,但當網格數增大到848 194 時,壓降的變化很小。考慮到計算成本和求解精度,本文選取網格數848 194 進行數值模擬。
3 模型驗證
為驗證數值方法的可靠性,需進行模型驗證。因為現存文獻中鮮有非均勻熱流條件下超臨界CO2的傳熱試驗,所以選取Kim 等人[12]在均勻熱流條件下進行的試驗中的1 組數據(G=238 kg/(m2·s),qwi=52 kW/m2,p=7.621 MPa)進行模型驗證,得到內壁溫和主流溫度沿管長的分布如圖3所示。結果表明,試驗和模擬所得內壁溫和主流溫度的誤差均在3%以內,認為模型可靠。
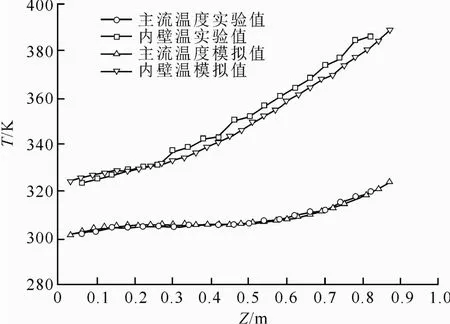
圖3 內壁溫和主流溫度沿管長的分布Fig.3 The distribution of inner wall temperature and bulk temperature along the tube length
4 結果與討論
4.1 均勻與非均勻加熱
與均勻加熱的情況不同,非均勻加熱時,管壁加熱面和未加熱面的局部熱流密度不同,壁溫和對流傳熱系數也不同。圖4給出了p=7.6 MPa、G=100 kg/(m2·s)、qwi=50 kW/m2工況下非均勻加熱和均勻加熱的對流傳熱系數和內壁溫隨流體主流溫度的變化曲線。
為便于比較,對于均勻加熱,熱流密度即實際施加于加熱面的熱流密度;對于非均勻加熱,熱流密度為整個圓周面的平均熱流密度,實際每處的熱流密度并不相同。其中,加熱面對流傳熱系數定義如下:
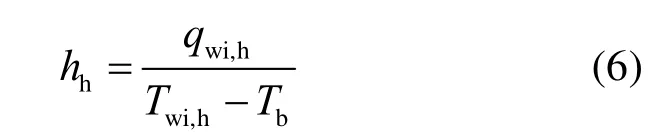
未加熱面對流傳熱系數定義如下:
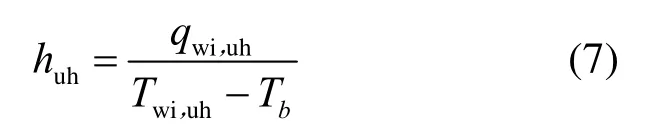
總對流傳熱系數定義如下:
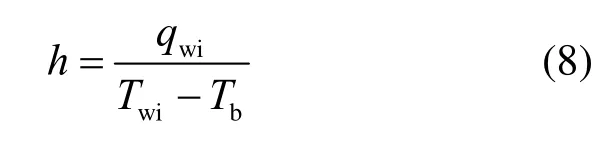
式中,hh、huh、h為加熱面對流傳熱系數、未加熱面對流傳熱系數、總對流傳熱系數,kW/(m2·K);Twi、Tb為內壁面溫度和主流溫度,K。
由圖4a)可知,2 種加熱情況對應的對流傳熱系數變化趨勢相同:擬臨界點前,都隨比定壓熱容的增大而增大;擬臨界點后,隨比定壓熱容的減小而減小。非均勻加熱時,未加熱面的對流傳熱系數最大,加熱面的對流傳熱系數最小;均勻加熱時,加熱面的對流傳熱系數則介于兩者之間。
圖4b)的內壁溫變化反映著圖4a)中對流傳熱系數的變化:非均勻加熱時,加熱面的局部熱流密度最大,對流傳熱系數最小,內壁溫最高。因此,較之均勻加熱,非均勻加熱受熱面壁溫更容易超溫。
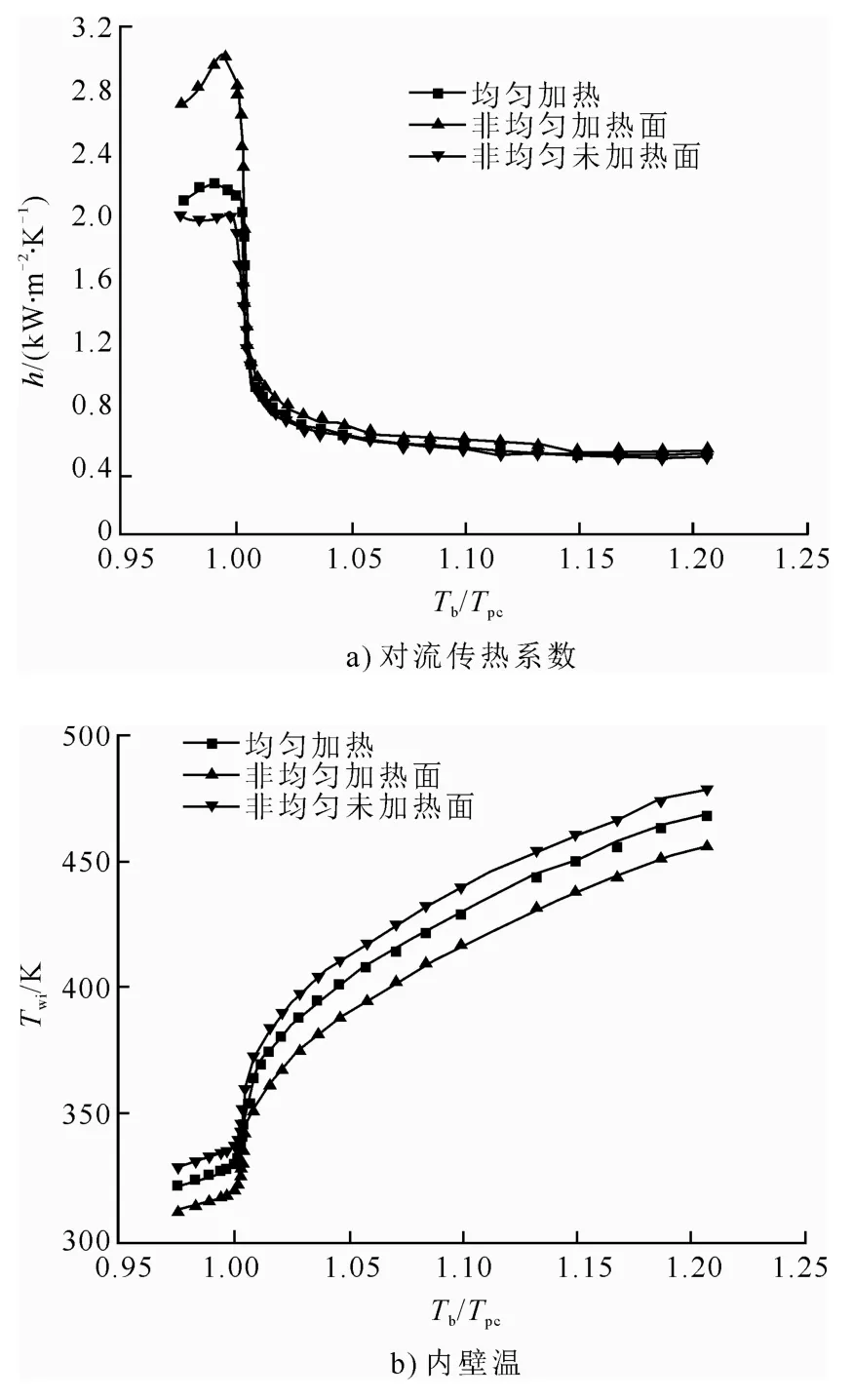
圖4 對流傳熱系數和內壁溫變化曲線Fig.4 Change curves of the convective heat transfer coefficient and inner wall temperature
4.2 非均勻加熱熱流密度的影響
圖5為G=100 kg/(m2·s)、p=7.6 MPa 工況下,熱流密度對非均勻傳熱的影響。
由圖5a)可以看出,3 種熱流密度條件下,總對流傳熱系數隨主流溫度的升高先增大后減小,在擬臨界點附近出現峰值。擬臨界點前,熱流密度越小,對流傳熱系數越大;擬臨界點后,3 種熱流密度下的對流傳熱系數相差甚微。這是因為:擬臨界點前流體因溫度升高比定壓熱容不斷增大,傳熱能力增強;而以上3 種工況對應的Gr/Re2.7均大于文獻[17]所提到的臨界值10?5,傳熱受物性和浮力2 種因素的影響;由圖5b)可知,熱流密度越大,浮力越大,浮力效應對傳熱的抑制越嚴重。因此:28 kW/m2熱流密度下的對流傳熱系數最大,39 kW/m2次之,50 kW/m2最小;擬臨界點附近,Gr/Re2.7驟減,浮力對傳熱的抑制驟減,對流傳熱系數達到峰值;擬臨界點后,流體比定壓熱容減小,傳熱系數減小;遠離擬臨界點的位置,流體的比定壓熱容隨主流溫度變化不大,3 種工況對應的Gr/Re2.7也隨主流溫度變化不大,且相差甚微。

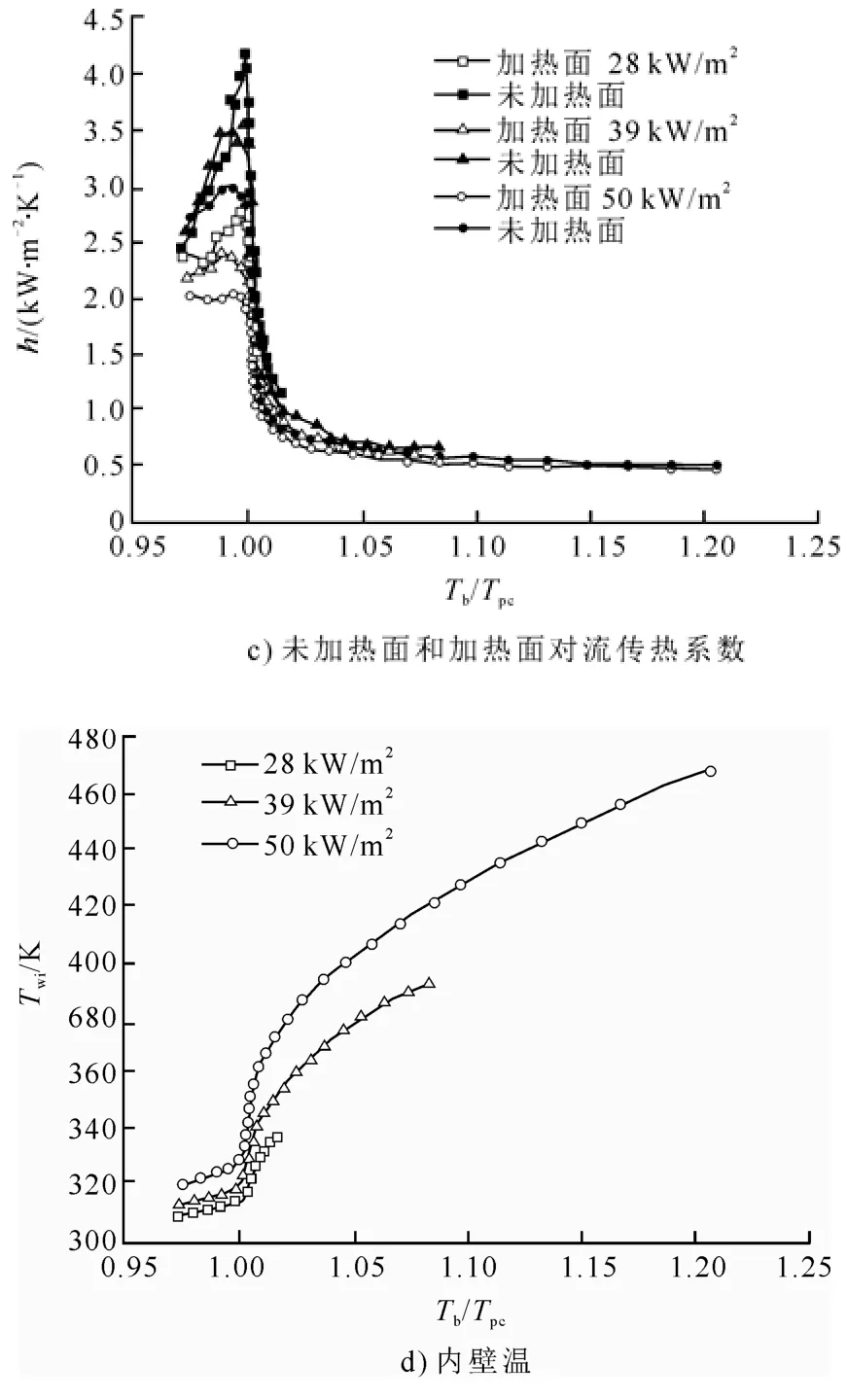
圖5 熱流密度對非均勻傳熱的影響Fig.5 Effects of heat flux on non-uniform heat transfer
圖5c)給出了3 種熱流密度條件下管壁加熱面和未加熱面對流傳熱系數的變化。總體趨勢和圖5a)相同,但擬臨界點前,未加熱面的對流傳熱系數大于加熱面的對流傳熱系數,擬臨界點后,兩者相差較小。這是因為,擬臨界點前,加熱面內壁溫和主流溫度相差較大而未加熱面內壁溫和主流溫度相差較小,隨著管壁周向導熱和流體對流傳熱的不斷進行,未加熱和加熱面的內壁面溫差逐漸減小,因此,擬臨界點后對流傳熱系數的差值也逐漸減小。
圖5d)給出了3 種熱流密度下內壁溫隨主流溫度的變化。熱流密度越大,內壁溫越高。擬臨界點前,內壁溫變化平緩;擬臨界點后,內壁溫飛升;遠離擬臨界點的位置,溫度變化又變得平緩。這與圖5a)中對流傳熱系數的變化一致。
4.3 非均勻加熱入口壓力的影響
選取p=7.6、8.0、8.6 MPa 共3 組工況(G=100 kg/(m2·s),qwi=50 kW/m2),分析入口壓力對非均勻傳熱的影響,如圖6所示。
由圖6a)可以看出,不同于低熱流密度下壓力對對流傳熱系數的影響,在本文所給的高熱流密度下,入口壓力越大,對流傳熱系數越大。結合圖6b)可知,在當前熱流密度下,Gr/Re2.7遠大于文獻[17]提到的Gr/Re2.7臨界值10?5,浮力對傳熱的抑制作用十分明顯。擬臨界點前,流體因不斷吸熱,溫度升高,比定壓熱容逐漸增大,傳熱能力增強;擬臨界點處,流體比定壓熱容達到峰值,對流傳熱系數也達到峰值;擬臨界點后,流體比定壓熱容驟減,對流傳熱系數減小;遠離擬臨界點的位置,流體比定壓熱容變化緩慢,對流傳熱系數隨之變化緩慢。7.6 MPa 入口壓力下流體的物性隨主流溫度變化的劇烈程度大于8.0 MPa 和8.6 MPa 壓力下物性變化程度,管內近壁區流體與主流區流體密度差更大,導致浮力更大,對湍流傳熱的抑制作用更強。所以,入口壓力較大的一組,對流傳熱系數更大。熱流密度較低時,物性變化引起的浮力效應較弱,甚至可忽略其對湍流傳熱的抑制作用,此時,比定壓熱容的變化對湍流傳熱起主導作用。因此,在低熱流密度下,壓力越小,對流傳熱系數越大。
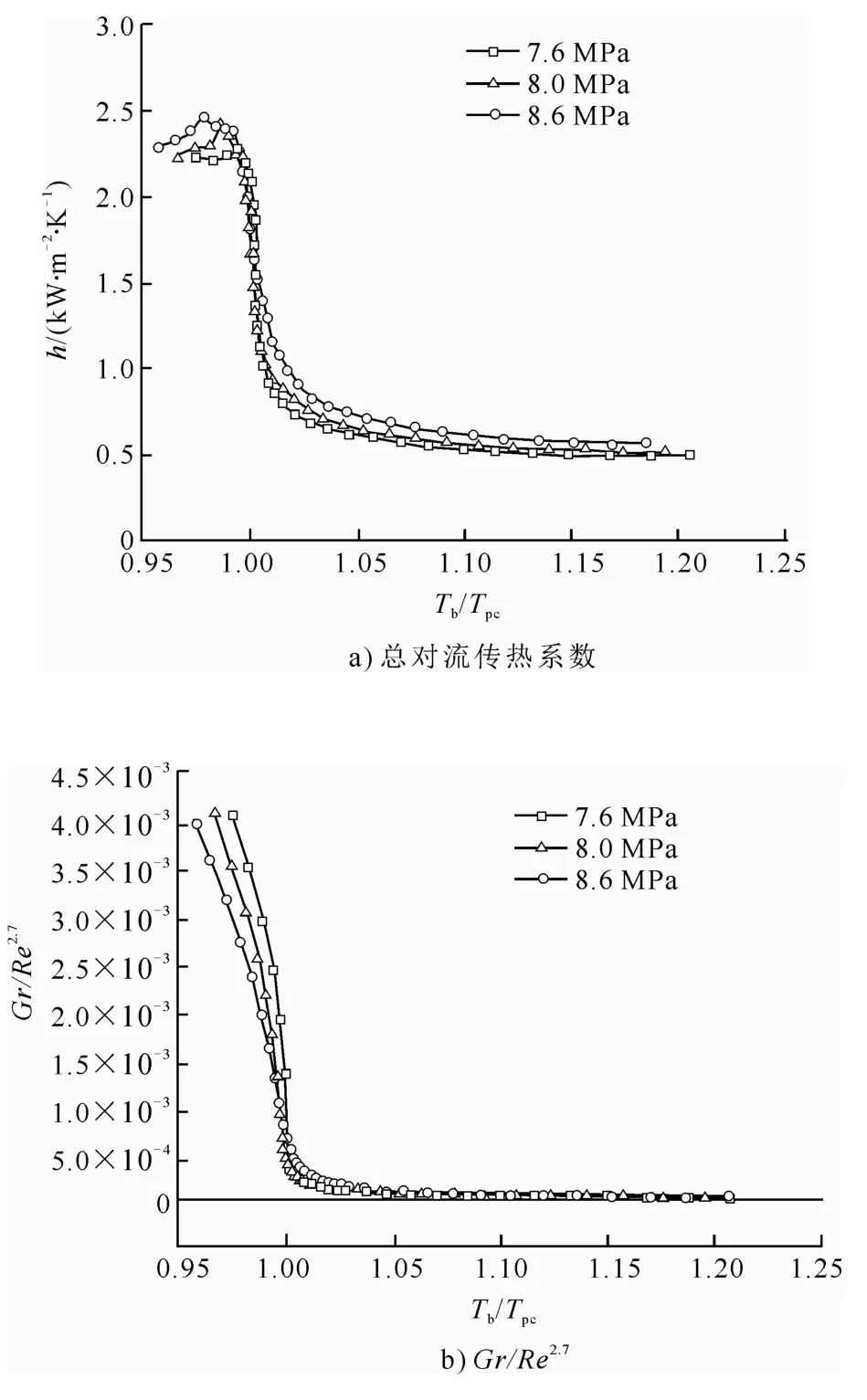
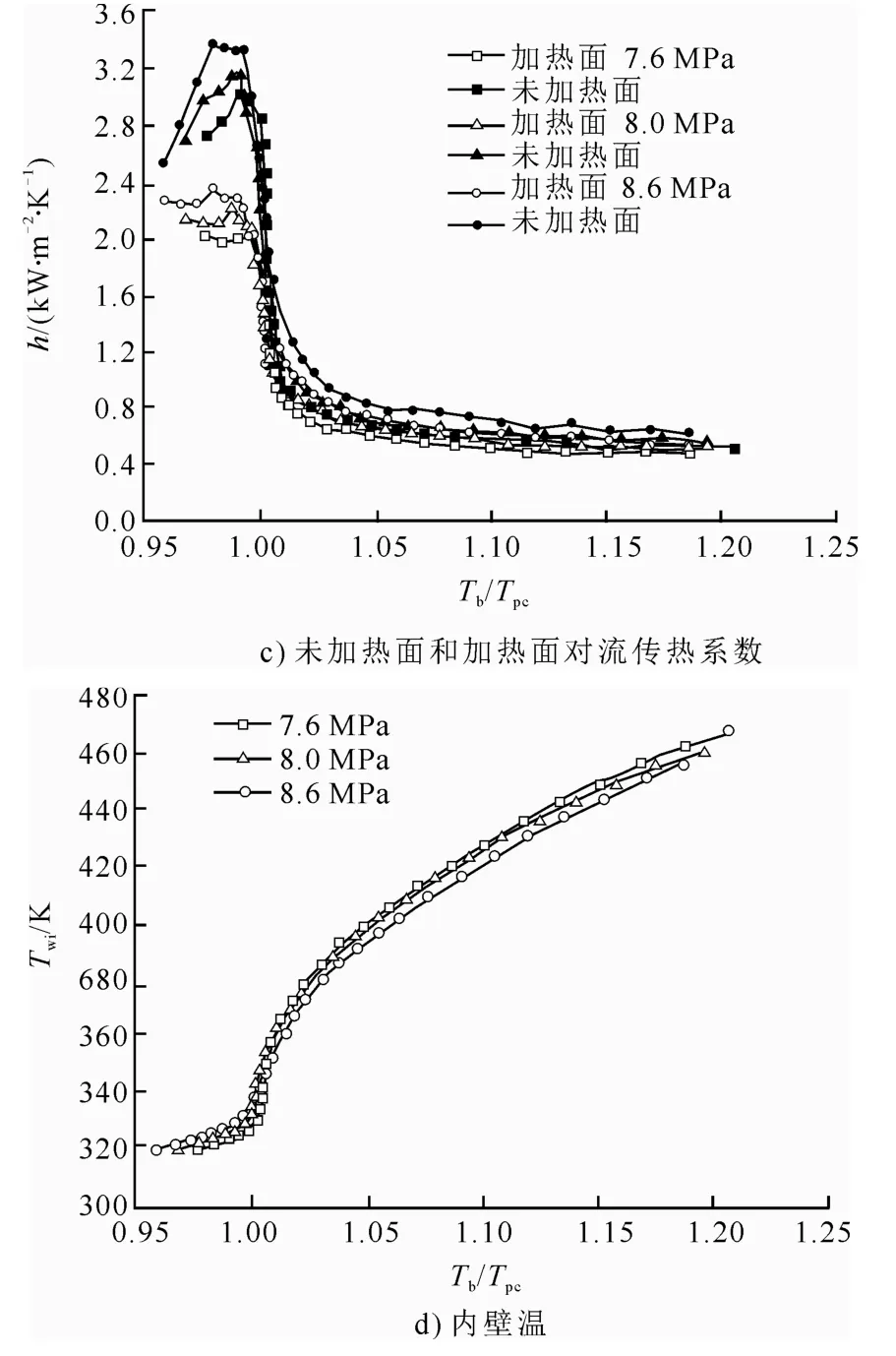
圖6 入口壓力對非均勻傳熱的影響Fig.6 Effects of inlet pressure on non-uniform heat transfer
圖6c)對比了3 種入口壓力下,管壁加熱面和未加熱面對流傳熱系數的變化。總趨勢同圖6a)。
圖6d)給出了3 種入口壓力下內壁溫隨主流溫度的變化曲線。由圖6d)可知,8.6 MPa 入口壓力對應的內壁溫較低,但與其他2 個條件下的內壁溫相差不大。
4.4 熱流密度和入口壓力對加速效應的影響
除CO2物性變化和浮力影響外,加速效應也是一個影響超臨界CO2在管內傳熱流動的重要因素。由前文可知,因流動過程的壓降遠小于入口壓力,可忽略壓降引起的加速效應。但是,隨著管內流體溫度的升高、密度的降低和熱膨脹系數的變化,軸向的密度差也會使流體產生加速效應,進而使流體速度梯度發生變化,切應力隨之變化,影響湍流的生成、擴散和傳熱能力,嚴重時易引發湍流的層流化。McEligot 等人[18]研究了湍流向層流轉變過程中的傳熱特性,提出了無量綱準則數Kv的表達式(式(9)),以判別因密度差引起的加速效應對管內超臨界流體傳熱的影響。
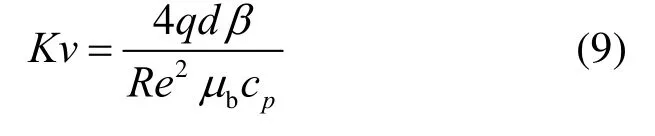
當Kv<3×10?6時,流動狀態保持為湍流;當Kv≥3×10?6時,湍流減弱,傳熱惡化。
圖7給出了熱流密度和入口壓力對加速效應的影響。
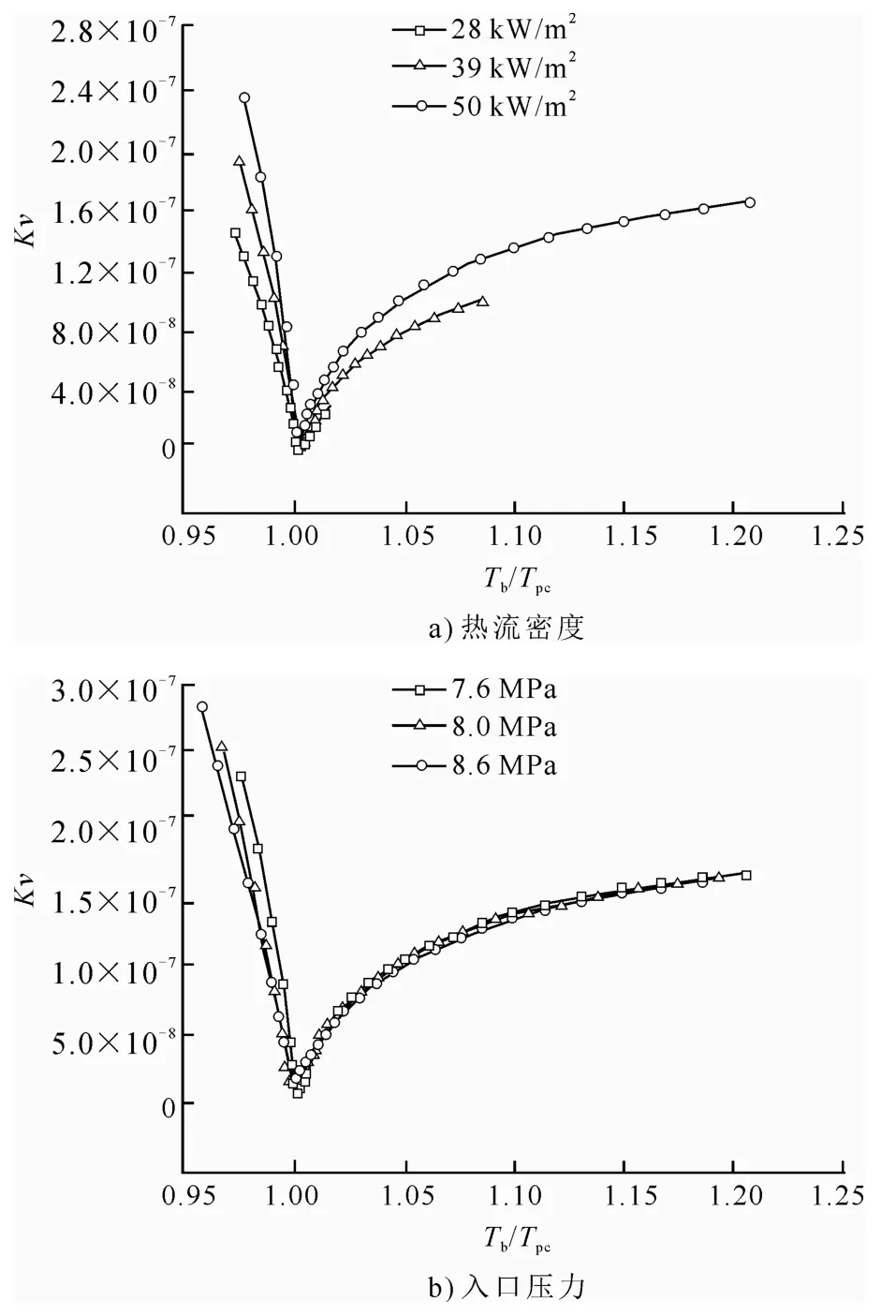
圖7 熱流密度和入口壓力對加速效應的影響Fig.7 Effects of heat flux and inlet pressure on acceleration effect
由圖7a)可知,Kv隨主流溫度的升高先減小后增大,擬臨界點為最小值。正如式(9)所示:隨著溫度的升高,流體的比定壓熱容增大,在擬臨界點處達到最大值,此時Kv最小;擬臨界點后,隨著流體比定壓熱容減小,Kv逐漸增大。而熱流密度越大,流體軸向密度場分布越不均勻,加速效應就越強。
由圖7b)可知,Kv的變化與入口壓力對浮力效應的影響類似:壓力越小,Kv越大,加速效應就越強。原因是7.6 MPa 下CO2的物性變化較8.0 MPa和8.6 MPa 更為劇烈。比較熱流密度和入口壓力的影響可知,熱流密度對加速效應的影響更大,這一點從Kv的表達式也可以看出。本文所有工況得到的Kv都遠小于臨界值,因此,加速效應的影響可忽略。
4.5 模擬結果與現有關聯式的比較
對于亞臨界單相流體,經典的Dittus-Boelter 關聯式[19]對傳熱有著較好的預測,而超臨界流體因其物性在擬臨界點劇烈變化,以及引起的浮力和加速效應,使得Dittus-Boelter 關聯式所預測的傳熱特性和試驗結果存在很大偏差。針對這一問題,許多學者在各自試驗的基礎上,提出了許多超臨界CO2在不同條件下的傳熱關聯式。這些關聯式大多把主流區流體和近壁區流體物性的比值作為修正項引入Dittus-Boelter 關聯式。表2給出了4 種常見的傳熱關聯式。

表2 4 種常見的傳熱關聯式Tab.2 Four kinds of heat transfer correlations
圖8為G=100 kg/(m2·s)、qwi=50 kW/m2、p=7.6 MPa 條件下由表2中傳熱關聯式計算所得Nu和本文模擬值對比。由圖8可見,不同傳熱關聯式所得Nu相差很大,擬臨界點附近更為明顯。并且,4 種關聯式預測的Nu與本文模擬值相差很大,主要原因在于本文所給的計算模型為非均勻熱流密度下的豎直圓管內超臨界CO2傳熱,而4 種關聯式是針對均勻熱流密度得到的,因此僅適用于各自的試驗工況。
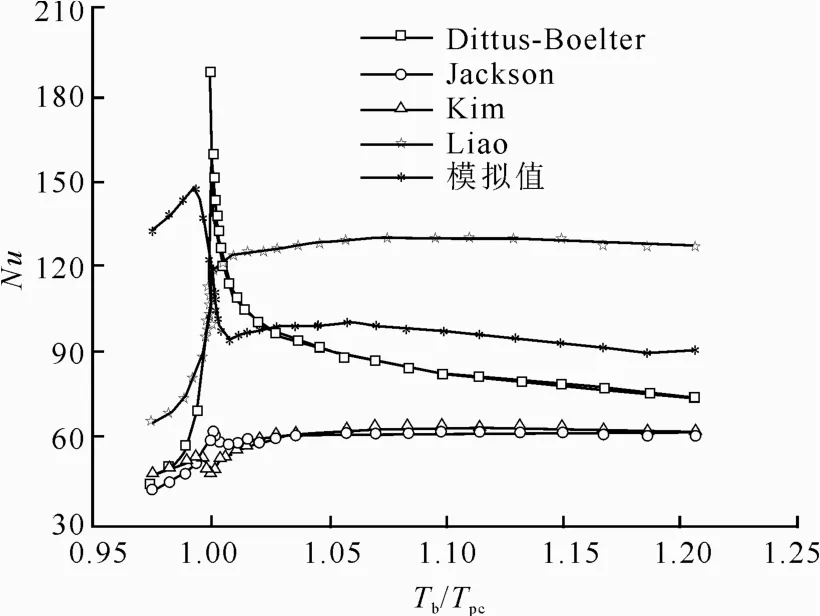
圖8 4 種常見傳熱關聯式計算Nu 與模擬值對比Fig.8 The Nu calculated by the above four common correlations and the simulated values
為較為準確地預測依據本文計算模型所得Nu,在Dittus-Boelter 關聯式的基礎上,結合浮力效應和物性變化,提出以下關聯式:
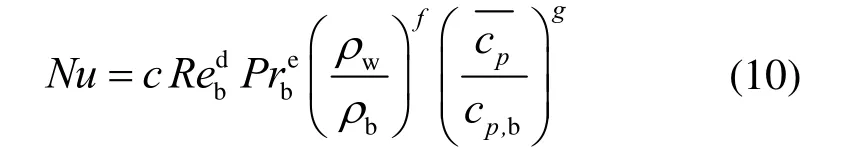
式(10)中,浮力效應由近壁區流體和主流區流體的密度差產生,因此,用近壁區流體和主流區流體的密度之比作為浮力修正項。物性變化中,比定壓熱容的變化最明顯,采用平均比定壓熱容與主流區流體比定壓熱容之比作為物性修正項。由4.4 節可知,加速效應的影響可忽略不計。利用多元線性回歸的方法求得以下傳熱關聯式:
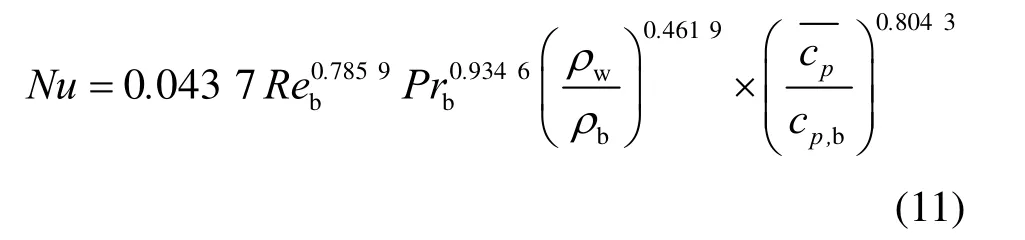
任意選取3 組工況,比較新關聯式計算的Nu和本文模擬值,結果如圖9所示。由圖9可見,新傳熱關聯式與模擬值吻合較好。但應注意,雖然超臨界CO2的傳熱規律具有一定的相似性,但CO2物性的劇烈非線性變化及其帶來的浮力效應和加速效應給研究帶來了很大的困難。目前,還不存在一個普遍適用且準確的傳熱關聯式。因此,新關聯式也只適用于本文中的數據。
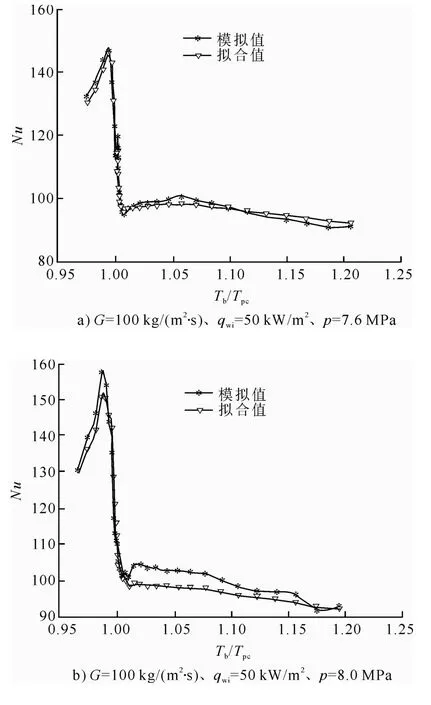
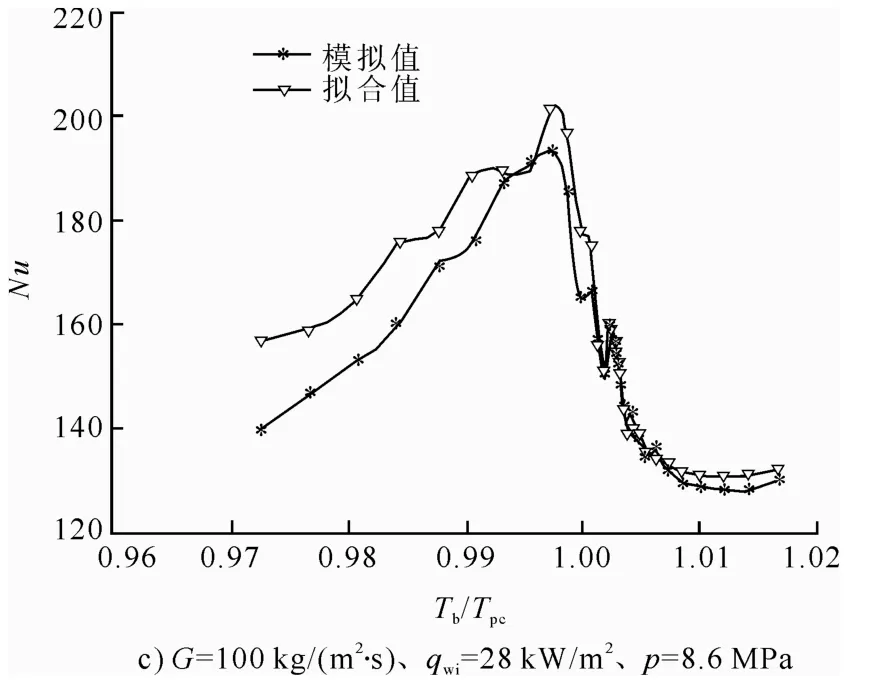
圖9 新關聯式計算Nu 與模擬值對比Fig.9 The Nu calculated by the new proposed correlation and the simulated values
5 結 論
1)相同加熱量條件下,與均勻加熱相比,非均勻加熱局部熱流密度大,對流傳熱系數小,內壁溫更高。
2)在壓力和質量流速一定的情況下,增大熱流密度,對流傳熱系數減小,浮力和加速效應增強;在高熱流密度下,增大入口壓力,對流傳熱系數增大,浮力和加速效應減弱。
3)對于非均勻加熱圓管,未加熱面的對流傳熱系數大于加熱面的對流傳熱系數,隨著周向導熱和對流的作用,兩者之差逐漸減小。
4)新的傳熱關聯式能較好地預測文中超臨界CO2的傳熱規律。

