時頻系統數字鎖相技術研究

王鵬宇 楊志剛 鄭麗麗

(中國電子科技集團公司第二十七研究所，河南鄭州 450047)

1 引 言

隨著航天測控系統的發展，測量設備對頻率標準的精度(準確度)和穩定度要求越來越高。通常情況下基于單一銣鐘頻率源的頻標基準，其準確度指標很高，但短期穩定度一般不高；而基于單一晶振頻率源的頻標基準，雖然能夠達到很好的短期穩定度，但準確度又不高。為全面提高頻標基準的長短期穩定度指標，目前一般采用基于GPS馴服、鎖相技術的解決方案。

鎖相環的設計主要考慮穩定性、帶寬和噪聲性能[1,2]。頻標基準最早采用的是模擬鎖相環，由本振跟蹤外參考頻率信號。模擬鎖相環的特點是成熟、可靠性好、鎖定速度快；但參數設置不靈活，分析困難，一致性較差，不能跟蹤1PPS時間基準信號。

隨著衛星導航系統的出現，上世紀90年代初提出了利用衛星導航系統提供的1PPS時間基準信號馴服本地頻率源的方案，這樣可以使本地時統設備的1PPS精度和10MHz信號的長期穩定度溯源到衛星導航系統的時間基準上。本文即討論外部1PPS或10MHz頻率信號馴服銣鐘或晶振的數字二階/三階鎖相環結構，建立了頻標模塊的仿真模型，給出了參數設置依據、仿真及硬件測試結果，驗證了模型的正確性。

2 頻標模塊模型

時頻系統中的頻標模塊結構如圖1所示，其主要功能是對外提供具有高精度和高穩定度的10MHz頻率信號和1PPS時間基準信號。當指標要求不是很高時，也可由GPS/BD(北斗)的1PPS信號直接馴服晶振，如圖1中虛線所示。

圖1 頻標模塊結構組成框圖Fig.1 Frequency standard component structure

數字鎖相環主要利用1PPS脈沖進行鑒相(10MHz信號可分頻出1PPS脈沖)，因此以1s時間間隔作為相位2π，環路中用待馴服銣鐘/晶振等頻率源倍頻至f0后分出1PPS與參考輸入1PPS之間的時間差進行采樣，所以，相位差Δφ與采樣計數N及f0之間的關系為

(1)

而相位差也可以用時間差來表示為

(2)

頻標模塊的仿真模型如圖2所示。

圖2 頻標模塊仿真模型組成框圖Fig.2 Frequency standard component simulation model

2.1 待馴服頻率源模型

待馴服頻率源建模主要考慮的是自身噪聲和老化率。以高穩晶振為例，若10MHz晶振秒穩優于5E-13，相當于頻率穩定度標準差最大為5E-6Hz，即頻率變為10 000 000.000 005Hz，換算成秒時間周期為0.999 999 999 999 5s，變化了5E-04ns，即可以將晶振建模為標準差為5E-04ns相位累加器。

晶振的老化率為[3]

(3)

式中：fx(t)——被測頻率的瞬時值；fr(t)——參考頻率的瞬時值；fx0——兩者頻率的標稱值；τ——平均時間。

為了便于仿真，令

fr(t)=fx0

且

fx(t)>fr(t)

所以，若按晶振日老化率為1×10-10/d，則有

即

fx(t)-fx0=fx0×10-10/(3 600×24)Hz/s

若晶振標稱頻率為10MHz，則可得本振相位變化率為

107×10-10×2π/(3 600×24)=7.272 2E-8rad/s

2.2 GPS/BD 1PPS信號模型

假設GPS/BD接收機的授時精度優于20ns(1σ)，則輸入1PPS信號相位抖動的標準差為1.256 6E-7rad。設環路啟動初始時間差500ns，即相位差3.141 6E-6rad。

2.3 鎖相環結構

當系統采樣率ws達到ws>10wc(wc為穿越頻率)時，數字鎖相環可以由一個模擬鎖相環通過同步采樣來獲得[4]。經過推導，二階鎖相環的數字化結構如圖3所示。

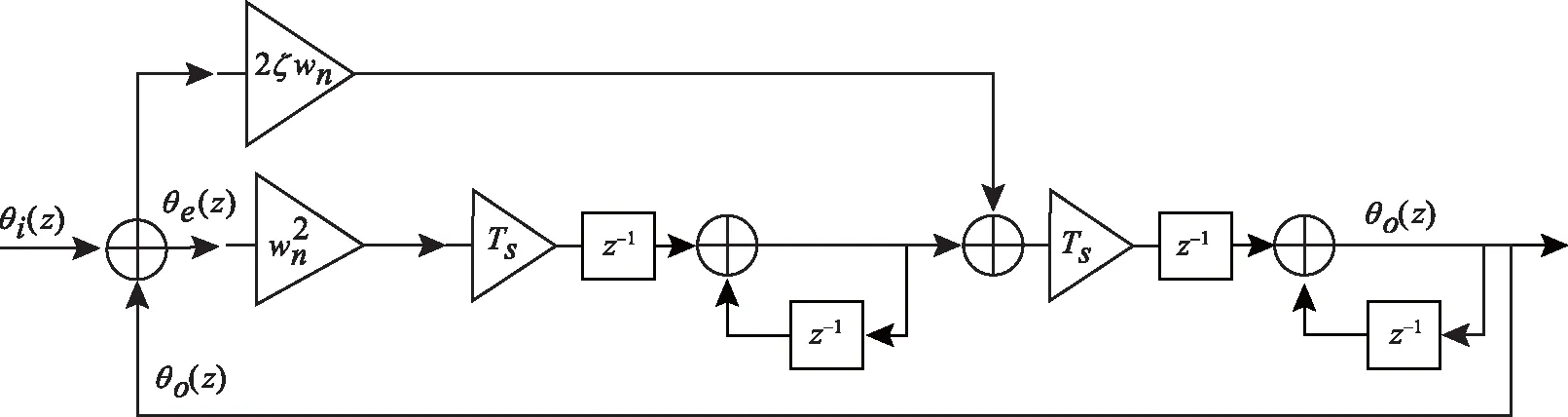
圖3 二階數字鎖相環示意圖Fig.3 2 order digital PLL

圖3中，θi(z)為輸入相位，θo(z)為本振輸出相位，θe(z)為相位差，它們的單位均為弧度。ζ和wn是二階控制系統的固有頻率和阻尼，Ts為環路更新周期。二階鎖相環的等效噪聲帶寬BL可以表示為

(4)

式(4)中，wn的單位為rad/s，而BL的單位為Hz。綜合考慮環路動態性和響應時間，一般ζ取0.707，因此二階環路的可控參數只有環路帶寬BL。又因為ws>10wc，可導出ws>30BL，即

(5)

式(5)給出了頻標模塊鎖相環噪聲帶寬的上限。

頻標模塊的主要任務是對外提供高精度1PPS信號，通常要與GPS/BD接收機給出的1PPS信號一致。而當環路帶寬較窄時，由于晶振老化率的影響，造成二階環路鎖定后的鑒相輸出不為零，即本振輸出1PPS信號與參考輸入1PPS信號的相位不一致。此時可以采用三階鎖相環，如圖4所示[5,6]。

圖4 三階數字鎖相環Fig.4 3 order digital PLL

圖4中，環路增益k′1，k′2，k′3由式(6)確定

k′1=(k+2)ζwn

(6)

考慮到環路穩定性，需滿足k>0，ζ>0.25。而為了使環路動態性能可以由二階系統近似，要求k>5。當k=6時，可以得到BL與ζ，wn之間的簡單關系。此時，BL可以由式(7)近似估算

BL=(2.037ζ+0.1036)wn(ζ>0.2)

(7)

當ζ=0.707時，三階環路性能也可以只通過環路帶寬BL來控制。

開環、二階環路、三階環路時本振相位輸出與外參考信號對比如圖5所示。可見晶振的老化使得其輸出相位與參考相比向一個方向不斷偏移；二階環路可以讓本振輸出相位跟隨外參考，但存在固定相差；當采用三階環路后，本振輸出相位跟隨外參考，且不存在固定相差。

圖5 開環、二階環路、三階環路本振相位輸出與外參考信號對比Fig.5 Local oscillator ouput compared with reference output when open loop,2order/3order pll loop

3 仿真分析

3.1 數字環路仿真分析

3.1.1鑒相器量化

鑒相器量化采用環路中用待馴服頻率源對其分頻后1PPS與參考輸入1PPS之間的時間差進行采樣的方式。不同量化靈敏度對于環路性能的影響如圖6所示。

圖6 量化靈敏度對于環路性能的影響曲線圖Fig.6 The effect on the pll performance by phase detector quantization

從圖6可以看出，鑒相器量化程度越高對提高環路性能越有利，將10MHz待馴服信號倍頻至1GHz對時間差進行采樣的環路性能要遠遠好于利用倍頻至50MHz信號進行采樣。然而在FPGA內部實現1GHz的信號處理是不現實的，必須在FPGA可實現情況下盡量提高時間差采樣率。同時，通過圖7可以看出，減小環路噪聲帶寬BL可以抵消鑒相靈敏度對環路輸出性能的影響。

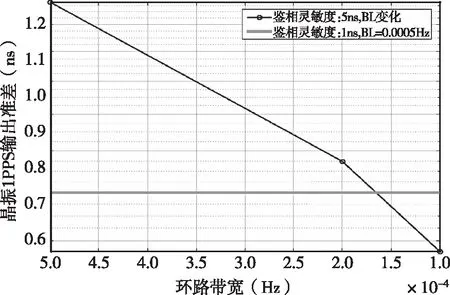
圖7 減小環路帶寬BL可以抵消鑒相靈敏度對環路輸出性能的影響Fig.7 The decrease of BL can compensate phase detector quantization decrease

3.1.2本振壓控壓DA器件量化

考慮晶振的數字控制對環路性能造成的影響。因為N位DA的量化誤差的方差為

若N位DA控制晶振的最大調整范圍為±5Hz，晶振標稱f0=10MHz，有f0·Δ·2N-1=5，則頻率控制步長為

DA的量化誤差方差為

DA量化位數對環路噪聲的影響如圖8所示。

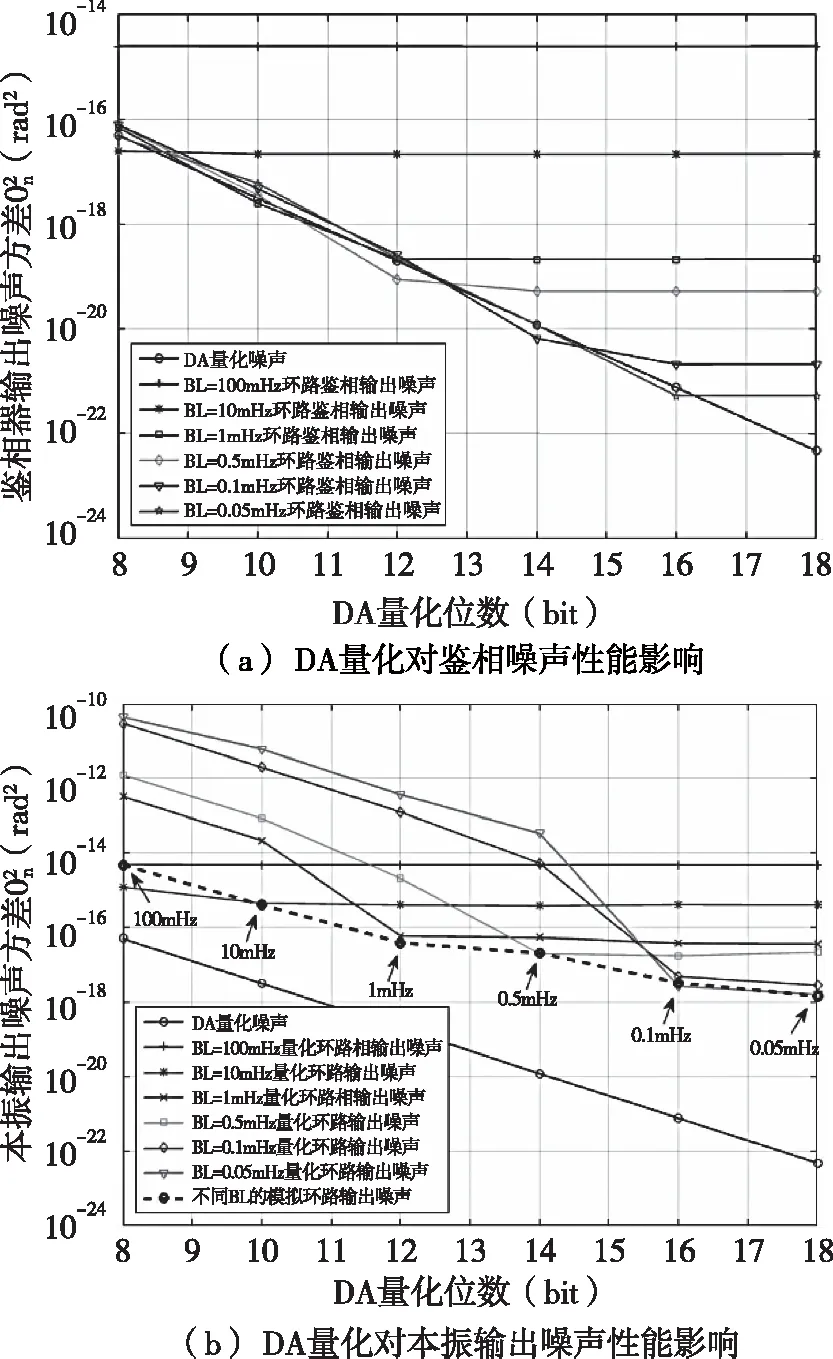
圖8 DA量化位數對環路噪聲的影響示意圖Fig.8 The influence of pll noise by DA quantization

可見，DA的量化位數限制了環路噪聲帶寬所能獲得的鑒相噪聲性能，進而決定了環路最小可設的有效帶寬BL。由于晶體老化的影響，在環路帶寬過低時，DA量化會造成相位輸出起伏，反而使環路噪聲性能嚴重惡化。本振存在老化時，不同帶寬下DA量化(16bit)與非DA時輸出噪聲方差(rad2)比值如圖9所示。

圖9 不同帶寬下DA量化(16bit)與非DA時輸出噪聲方差(rad2)比值示意圖Fig.9 The ratio of local oscillator noise variance between DA(16bit)and pure analog

從圖9可以看出，噪聲帶寬不易過小，否則DA量化噪聲會造成輸出噪聲性能惡化。

同時，DA位數也決定了輸出頻率的準確度[7]。若頻率輸出準確度要求優于1×10-11，按1×10-12設計，則對于控制電壓為(0～5)V，頻率變化范圍±3Hz的10MHz晶振來說，通過壓控壓分辨率求DA位數N，有

(8)

由式(8)可知，DA至少為20位。

3.1.3環路的定點運算

Matlab模型中各模塊內部運算與輸出均為實數表示，盡管考慮了量化，但由于模型內部模塊為浮點雙精度數表示，具有足夠精度，且積分器不設上限。因此，須考慮實際使用中FPGA內部的定點數表示對環路性能的影響[8]。

環路數據位寬64bit，積分器位寬96bit時，環路浮點運算與定點運算在環路輸出噪聲性能上的比較如圖10所示。可見，采用適當位寬后環路定點運算近似于浮點運算。

圖10 環路浮點運算與定點運算在環路輸出噪聲性能上的比較曲線圖Fig.10 The comparison on local oscillator output performance between floating point and fixed point arithmetic

3.1.4DA輸出對相位噪聲性能的影響

若待馴服對象為高穩晶振，則需考慮DA輸出更新頻率對環路性能的影響。當數字鎖相環路的更新周期與外參考1PPS時間基準信號一致時，鎖相環輸出相當于1Hz低頻信號，若直接控制DA產生的壓控壓，則高穩晶振相位噪聲將會出現1Hz低頻信號的各次諧波，使得偏移(0.1～10)Hz的相噪惡化，如圖11所示。

圖11 1Hz DA輸出頻率對相噪的影響曲線圖Fig.11 The influence on local oscillator output phase noise by 1Hz DA update frequency

因此，鎖相環輸出后必須接帶寬<1Hz的數字低通濾波器。數字濾波器主要考慮截至頻率fc、濾波器階數和采樣頻率fs。截至頻率越小越有利于抑制相位噪聲，但由于濾波器帶寬與產生的附加延遲成反比，過大的延遲反而可能使環路失鎖，仿真結果表明，Fc=0.001Hz的1階butterworth濾波器即可，而1，2，3階Fc=0.000 1濾波器環路都會產生振蕩，如圖12所示。

圖12 數字濾波器階數、截至頻率對相位噪聲影響曲線圖Fig.12 The influence on DPLL phase noise by digital filter order and cut frequency

數字濾波器的采樣率越高，它所產生的混疊頻率越高，越容易被簡單模擬濾波器濾除，但高采樣率意味著高計算量和高功耗，由圖13給出的仿真結果可以看出，從相位噪聲抑制角度看，100Hz的數字濾波器采樣率已經足夠。

圖13 數字濾波器采樣率對相位噪聲影響曲線圖Fig.13 The influence on DPLL phase noise by digital filter sample frequency

4 實測結果

頻標模塊組成框圖如圖14所示。

圖14 頻標模塊組成框圖Fig.14 The composition of frequency standard component

為了驗證數字鎖相環頻標方案的可行性，以晶振8607作為參考源對頻標模塊進行測試，結果數據見表1和表2，曲線結果如圖15所示。

由測試結果可知，環路帶寬BL=0.005Hz的環路性能只是略低于BLD=0.003Hz，但BL=0.005Hz環路鎖定時間在1h左右，而BL=0.003Hz環路則>3h，所以工程上取BL=0.005Hz即可滿足要求。測試均采用了二階環路結構，因為由仿真可知當BL<0.000 2Hz時，才會出現環路穩態相差Δφ≠0情況。設計中數字低通濾波器截至頻率為fc=0.01Hz。

還可看出，在同樣環路帶寬BL下，GPS/BD馴銣鐘，銣鐘馴晶振的頻標結構性能要明顯優于GPS/BD直接馴晶振的性能。但在指標可接受情況下，采用GPS/BD直接馴晶振的結構可以大大降低頻標模塊的成本。

表1 數字鎖相環頻標模塊相位噪聲測試結果(單位:dBc/Hz)Tab.1 Digital PLL frequency standard component phase noise test result(unit:dBc/Hz)相噪頻偏0.001Hz0.1Hz1Hz10Hz備注高穩晶振參數——<-113<-143—恒壓-37.9-81.1-112.3-136.8—BLD=0.007Hz-33.4-57.3-92.8-129.9—BLD=0.005Hz-34.7-77.8-112.5-136.8—BLD=0.005Hz-25.9-71.5-112.7-136.8GPS馴晶振BLD=0.003Hz-37.0-80.4-112.8-136.9—

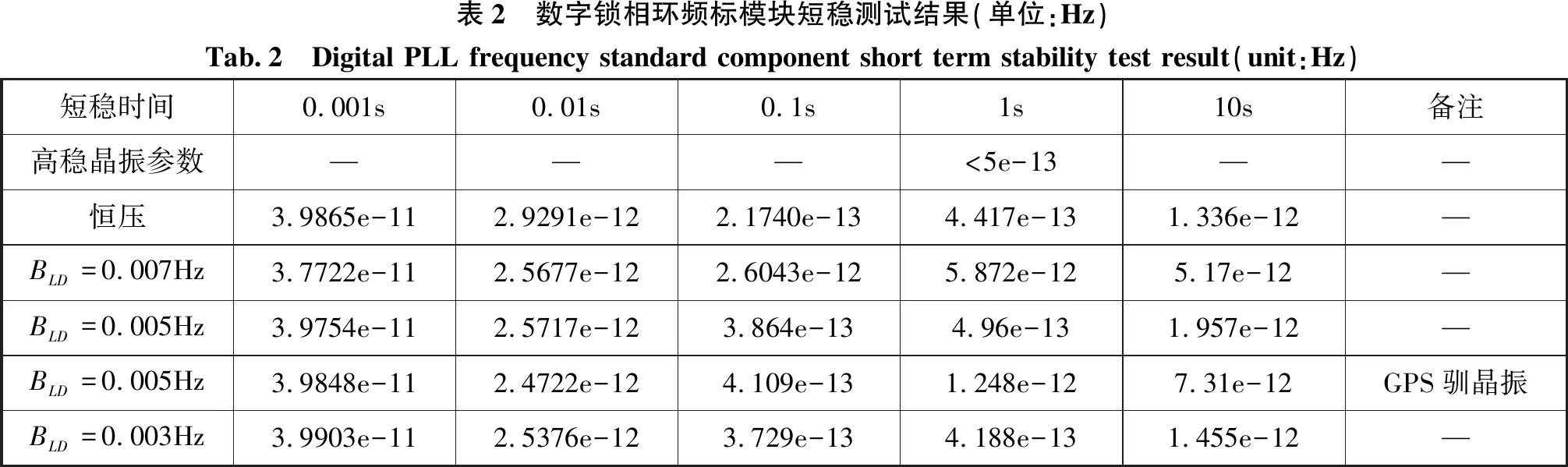
表2 數字鎖相環頻標模塊短穩測試結果(單位:Hz)Tab.2 Digital PLL frequency standard component short term stability test result(unit:Hz)短穩時間0.001s0.01s0.1s1s10s備注高穩晶振參數———<5e-13——恒壓3.9865e-112.9291e-122.1740e-134.417e-131.336e-12—BLD=0.007Hz3.7722e-112.5677e-122.6043e-125.872e-125.17e-12—BLD=0.005Hz3.9754e-112.5717e-123.864e-134.96e-131.957e-12—BLD=0.005Hz3.9848e-112.4722e-124.109e-131.248e-127.31e-12GPS馴晶振BLD=0.003Hz3.9903e-112.5376e-123.729e-134.188e-131.455e-12—

圖15 數字鎖相環頻標模塊實測結果示意圖Fig.15 Digital PLL frequency standard component test result

5 結束語

本文利用數字鎖相環技術完成了時頻系統中的頻標模塊設計。鎖相環鑒相為1PPS脈沖比相方式。環路設計包括本地頻率源模型、外部參考1PPS信號模型、二階/三階環路濾波器設計等。在硬件實現時需要考慮環路噪聲帶寬及各組成部分量化，浮點數、定點數表示對環路噪聲性能的影響。DA輸出應當考慮數字環路所特有的低頻信號諧波問題，而須外加帶寬<1Hz的低通濾波器。