基于粒子群優化的毫米波通信網絡資源分配算法

黃澄

摘 要：由于傳統的信道資源分配問題解決速度慢且頻率利用率較低，針對毫米波通信資源分配問題，設計了一種基于粒子群算法（PSO）的毫米波通信資源分配算法。在傳統的粒子群優化算法求解信道分配問題的基礎上，對于粒子群優化算法的缺點—易陷入局部最優解，提出了一種通過調整慣性權重的改進粒子群優化算法。仿真結果表明，與其他方法相比，改進后的粒子群優化算法具有更快的收斂速度和更高的收斂率。

關鍵詞：毫米波通信;粒子群算法;資源分配;信道分配;收斂;頻譜

中圖分類號：TP39文獻標識碼：A文章編號：2095-1302（2019）11-00-03

0 引 言

隨著技術的發展和進步，無線通信技術已成為生活中不可或缺的通信渠道。移動通信的運營商已采取增加基站數量等措施來解決網絡需求過大的問題，但無線通信與需求之間仍存在不可避免的矛盾。在為解決上述問題而提出的通信技術中，文獻[1]提出對移動網絡架構采用有效的資源管理和調度策略，以提高無線資源的利用率;文獻[2]提出使用終端直接D2D技術來提高頻譜效率。

另外，在實際通信環境中，來自信道之間的干擾會對通信系統產生較大影響。文獻[3]考慮了無線頻譜資源分配中的頻譜復用，為用戶提供更好的通信質量和容量以及更大的適用范圍。然而，低頻頻譜資源相對稀少，難以滿足高通信速率的要求。于是，人們將注意力轉向毫米波，毫米波頻段寬且有效的頻帶范圍廣。在頻率資源緊張的背景下，更寬的頻帶無疑非常有吸引力。在參考文獻[4]中對毫米波進行資源分配，此資源分配的現有研究是在28 GHz毫米波帶寬下進行的，作者提出了一個約束干擾值來提高系統吞吐量。

毫米波無線資源分配問題可以被建模為給定無線電發射機形式的優化問題，工作頻率依據約束分配給無線電發射機，并將給定目標函數值最小化。這個問題屬于NP-hard問題，傳統方法需要較長時間來尋找最優解。元啟發式算法是解決此類問題的有效方法。不同的研究者已提出了許多元啟發式方法來解決FAP問題，如神經網絡[5]、禁忌搜索[6]、量子遺傳算法[7]等。在人工智能算法中，粒子群優化收斂速率快的優勢被學術界廣泛關注。

本文使用自適應PSO算法來解決毫米波通信資源分配問題，并且將該算法進行改進。其基本思想是尋找一種逃避局部極小值的方法以更大概率尋求全局最優解。

1 毫米波網絡資源分配目標函數

1.1 MI-FAP問題的公式化

系統提供的服務有幾個質量指標，其中最重要的是分配算法中的代價函數的值，它取決于干擾矩陣。干擾矩陣反映了任意2個節點之間的最大干擾程度，其中不同矩陣中的元素值背后的物理量不同。FAP中可能引入互調干擾、相鄰信道干擾和其他類型干擾[8]，本文的干擾包括共信道干擾、鄰信道干擾和共小區干擾。

該模型的目標是通過最小化違反干擾約束來優化系統。通常用一個N×N維的兼容矩陣來表示干擾約束條件（N為總小區數）：

C中對角元素cii等于分配給同一小區i的任意兩個信道的最小間隔，矩陣中的非對角元素cij（i≠j）等于分配給不同小區i和j的信道的最小間隔。

小區的頻率需求數用矩陣D表示：

式中矩陣D中的第i個元素表示第i個小區需要di個信道。設fiq為給第i個小區分配信道q，fiq=1時，信道q被分配給小區i。

為了滿足需求向量的要求，如果小區i需要di個信道，則需要滿足下式：

適應度函數可以表示為：

由公式可知，違反信道約束的信道越少，適應度函數值越小。所以，本文需找到一個使S（F）最小且符合干擾約束的分配方案F。

當F使用最小間隔編碼時：

當di≤j≤dmax時，fij=0[9]。此時可以避免CSC違約，使適應度函數變為：

1.2 針對毫米波的頻譜設定

毫米波具有帶寬寬、傳輸質量高的特點，可以極大地提高系統容量和傳輸速率。然而，信號衰減和覆蓋距離短等缺點使其使用受到限制。國際電聯確定了未來5G通信系統的候選頻段，其中毫米波頻段包括24.25～27.5 GHz，37～40.5 GHz，42.5～43.5 GHz，45.5～47 GHz，47.2～50.2 GHz，50.4～52.6 GHz，66～76 GHz，81～86 GHz等8個已分配頻段與31.8～33.4 GHz，40.5～42.5 GHz，47～47.2 GHz等3個待分配頻段[10]。因此，本文研究的毫米波頻譜資源分配的信道為以上毫米波頻段。

2 基于粒子群的目標函數優化

粒子群算法（PSO）是人工智能算法之一。在PSO中，每個解值都是搜索空間中的一個粒子。每個粒子都有相應的適應值，這些適應度值由優化的適應度函數來評估。每個粒子都有一個速度變量，使其能夠追尋在問題空間中飛行的最佳解。

在每一代t中，每個粒子位置Pi（t）由以下2個“最佳”值更新：

（1）第一個是迄今為止最好的個人解決方案，此值記錄為Pbesti（t）;

（2）第二個“最佳”值是到目前為止在種群所有粒子中獲得的最佳值，該全局最佳值記作Gbest（t）。

找到2個最佳值后，根據式（7）和式（8）更新它們的速度和位置：

式中：Vi（t）為粒子在第t代的速度;Pi（t）為粒子在第t代的位置;ω（t）為慣性權重;參數Rand1和Rand2是[0，1]中的隨機數;變量c1和c2是學習因子。

通過這兩個更新機制，PSO可以迅速收斂到好的解決方案。另一方面，該算法的主要缺點是缺少避免過早收斂的機制，導致它停滯在局部最優水平。

3 改進的粒子群算法—慣性權重隨機調整策略

由上，粒子群優化算法的主要缺點是會陷入局部最優解，算法不穩定。慣性權重ω是粒子群算法中一個影響力較大的因素，它決定了原飛行速度對現飛行速度的影響。當ω較大時，局部搜索能力較弱;當ω較小時，局部搜索能力較強，但此時收斂速度較慢，全局搜索能力較弱，將陷入局部極值。因此，設定適當的慣性權重可以提高優化能力。

針對傳統粒子群優化算法的缺點，設計了一種調整慣性權重的粒子群算法，即將慣性權重設計為在一定范圍內的隨機變量：

改進后的算法可以收斂到全局最優解，更穩定且可能性更大。本文ω取1，ωdamp取0.7。

4 信道分配算法及步驟

4.1 粒子群算法與信道分配問題的對應關系

粒子位置Pi（t）對應于信道分配方案F（i）。粒子的當前適應度函數值對應于粒子位置信道分配方案的質量。適應度函數的值越小，表示違反約束的頻率點越小，并且越接近最優解。搜索最佳位置的速度值表示搜索最佳信道分配方案的速度，即算法的收斂速度。

在信道分配問題中，目的是求出最小干擾，即尋找最小化目標函數適應度S（F）的信道分配方案F。

4.2 信道分配算法

信道分配步驟如下。

（1）確定粒子群規模nPop、最大迭代次數MaxIt、可用頻譜最大值VarMax及其最小值VarMin。

（2）將群體中每個粒子的速度和位置初始化為隨機數，將個體的歷史最佳位置Pbest定義為初始隨機位置;群體最優的個體為當前的Gbest，計算個體歷史最佳位置和群組最佳位置的適應度函數值。

（3）模擬粒子群行為，計算每一代粒子的適應度函數。

（4）比較粒子當前的適應度particle（i）.Cost和其歷史最優值Pbest，如果當前適應度函數值優于其歷史最佳值，則當前位置被歷史最佳位置取代。

（5）比較粒子歷史最優值particle（i）.Best.Cost和全局最優位置的適應度值GlobalBest.Cost，如果粒子的particle（i）.Best.Cost小于GlobalBest.Cost，則使用粒子的歷史最優位置代替全局最優位置。

（6）按式（7）和式（8）更新每個粒子i的速度和位置。

（7）如果不滿足終止條件，則返回步驟（3），否則輸出Gbest并結束。

4.3 算法仿真

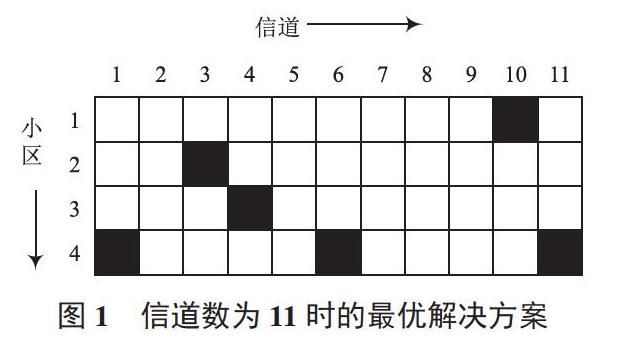
本文設計的算法用Matlab R2016b仿真，初始化種群數nPop=35，最大迭代次數MaxIt=500，可用頻譜最大值VarMax=30，最小值VarMin=3，學習因子c1=2，c2=2，慣性權重ω（t）=1，慣性重量阻尼比ωdamp=0.7。公式（10）展示了兼容性矩陣和需求向量，此時可供使用的最小信道總數應為11=1+5×2。圖1展示了該問題的最佳解決方案，其中黑色格子代表信道被分配給了對應小區。

圖2所示為算法可用信道數為11的仿真圖，橫縱坐標分別表示迭代次數和每代最小適應度函數值。由圖可知，粒子群算法在1代時就已經找到了最優解，此時干擾總數為4。

當頻譜資源平均分配，即為小區進行隨機頻譜分配時，此時的信道干擾函數適應度S（F）為69，遠大于利用粒子群算法進行頻率分配時的適應度值，說明信道干擾較多。

經過大量實驗驗證，改進后的算法可以更穩定地收斂到全局最優解。仿真問題的說明見表1，改進粒子群算法與傳統粒子群算法比較見表2。

5 結 語

本文研究了最小干擾下的頻率分配問題。在介紹了問題的概述和模型制定之后，提出了解決這一問題的方法。然后利用PSO算法生成最小干擾方案。仿真結果證明：本文改進的粒子群算法在解決毫米波信道分配問題上的尋優能力較強，算法收斂率和收斂速度都優于傳統粒子群算法。

參 考 文 獻

[1]賈叢富，肖靈.移動通信網絡中無線資源分配與調度策略[J].信息與電腦（理論版），2015（12）： 112-113.

[2]尹銘志.基于5G網絡的無線通信資源分配技術研究[A].中國計算機用戶協會網絡應用分會.中國計算機用戶協會網絡應用分會2018年第二十二屆網絡新技術與應用年會論文集[C]// 中國計算機用戶協會網絡應用分會：北京聯合大學北京市信息服務工程重點實驗室，2018：5.

[3]陳亮，楊奇.5G網絡中無線頻譜資源分配的進展分析[J].光通信研究，2016（6）：68-71.

[4] GUIZANI Z， HAMDI N. Spectrum resource management and interference mitigation for D2D communications with awareness of ber constraint in mmwave 5G underlay network [Z]. 2016.

[5] GUIRGUIS L A，GHONEIMY M M R E. Channel assignment for cellular networks based on a local modified hopfield neural network [J]. Wireless personal communications，2007，41（4）：539-550.

[6] HOUSSEM E H，MALIKA B. Integrating tabu search in particle swarm optimization for the frequency assignment problem [J]. 中國通信（英文版），2016（3）：137-155.

[7]徐雪飛，李建華，沈迪，等.基于量子遺傳算法的航空通信頻率動態分配[J].電訊技術，2015，55（12）：1311-1317.

[8] OSMAN M S A，ZEIN EL DIN R A，EMAM A M. Minimizing interference in frequency assignment problem based on guided particle swarm optimization algorithm [J]. International journal of scientific & technology research，2017（6）：176-183

[9]劉俊霞，賈振紅，覃錫忠，等.改進人工蜂群算法在信道分配上的應用[J].計算機工程與應用，2013，49（7）：119-122.

[10]黃杰.5G無線通信中的多頻段毫米波信道測量與建模[D].濟南：山東大學，2018.

[11] FUNABIKI N.A naural network parallel algorithm for channel assignment problems in cellular radio networks [J]. IEEE trans. veh.technol.，1992，41（4）：430-437.