利用柯尼希定理巧解質(zhì)點(diǎn)系的相對速度問題
鄭 金
(遼寧省凌源市職教中心,遼寧 朝陽 122500)
力學(xué)中的柯尼希定理反映了質(zhì)點(diǎn)系的總動(dòng)能的組成種類及其數(shù)量關(guān)系,即質(zhì)點(diǎn)系的總動(dòng)能等于質(zhì)心的動(dòng)能與各質(zhì)點(diǎn)相對于質(zhì)心運(yùn)動(dòng)的動(dòng)能之和,在二體問題中質(zhì)點(diǎn)系的動(dòng)能等于質(zhì)心動(dòng)能與相對動(dòng)能之和.可以證明,在質(zhì)心參考系中,兩個(gè)物體的相對動(dòng)能等于折合質(zhì)量與相對速度平方的乘積的一半.對于相互作用的兩個(gè)物體的相對運(yùn)動(dòng)問題可有多種解法,但利用柯尼希定理來解答,可化繁為簡.
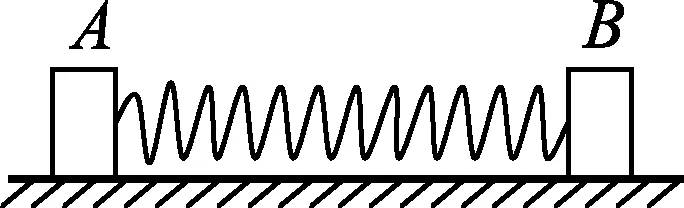
圖1
例1.如圖1所示,在光滑的水平面上,兩個(gè)物體A和B的質(zhì)量分別為m1和m2,中間用一根勁度系數(shù)為k的輕彈簧連接在一起.開始時(shí)兩個(gè)物體靜止,彈簧處于自然狀態(tài),現(xiàn)給物體A一個(gè)向左的初速度v0,彈簧始終處于彈性限度內(nèi),求兩個(gè)物體運(yùn)動(dòng)的相對位移為x時(shí)的相對速度為多大?
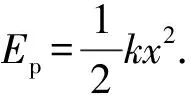
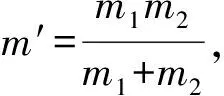
由于系統(tǒng)在水平方向不受外力,因此系統(tǒng)質(zhì)心的速度保持不變,對系統(tǒng)由動(dòng)量守恒定律有
m1v0=(m1+m2)vC,
根據(jù)柯尼希定理可知兩個(gè)物體的總動(dòng)能為
Ek=Ek′+EkC.
對系統(tǒng)由機(jī)械能守恒足律有Ek0=Ek+Ep.聯(lián)立方程可得相對速度大小為

例2.質(zhì)量分別為m和M的兩個(gè)物塊A、B用橡皮繩相連,放在水平臺面上,橡皮繩原長為a,當(dāng)它伸長時(shí),如同勁度系數(shù)為k的彈簧.物塊與臺面之間的動(dòng)摩擦因數(shù)為μ,現(xiàn)將它們拉開,距離為b(b>a),然后由靜止釋放,求兩物塊相碰時(shí)的相對速度.

圖2
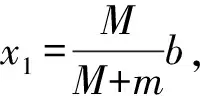
兩個(gè)物塊逐漸靠近,受到的摩擦力方向相反,考慮到二者質(zhì)量不等,設(shè)m W2=-f1(x1+x)-f2(x2-x)= 對系統(tǒng)由動(dòng)能定理和柯尼希定理得 W1+W2=Ek′+EkC, 解得 點(diǎn)評:解題關(guān)鍵是確定系統(tǒng)的質(zhì)心剛開始時(shí)的位置和相碰時(shí)的位置在何處并畫出示意圖,這樣在計(jì)算摩擦力做的功時(shí)才能確定對應(yīng)位移的大小和方向,同時(shí)還要考慮摩擦力的方向.設(shè)置的質(zhì)心位移x是未知量,在解方程時(shí)消去了.如果在地面參考系中認(rèn)為系統(tǒng)的質(zhì)心靜止不動(dòng),則不必對系統(tǒng)的質(zhì)心應(yīng)用動(dòng)能定理,而且在計(jì)算摩擦力對系統(tǒng)做的功時(shí)也不需考慮質(zhì)心的位移,雖然所得結(jié)果相同,但運(yùn)動(dòng)情況卻與實(shí)際不符.因?yàn)橛少|(zhì)心運(yùn)動(dòng)定理可知,在恒力作用下系統(tǒng)的質(zhì)心做勻加速運(yùn)動(dòng),不可能靜止,除非兩個(gè)物體的質(zhì)量相等. 對系統(tǒng)由動(dòng)能定理和柯尼希定理有 W1+W2=Ek′+EkC, 解得 例3.在光滑水平面上有兩個(gè)物體A、B,其質(zhì)量分別為m1、m2,它們沿同一直線運(yùn)動(dòng)并發(fā)生碰撞.碰撞前A、B的速度分別為v1、v2,碰撞后的速度分別為v1′、v2′,試分析v1′、v2′滿足什么關(guān)系時(shí),碰撞過程中損失的機(jī)械能最大? (a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2+…+anbn)2, 需將末動(dòng)能的關(guān)系式變形為 由柯西不等式可知 (m1+m2)(m1v1′2+m2v2′2)≥ (m1v1′+m2v2′)2. 由動(dòng)量守恒定律有 m1v1+m2v2=m1v1′+m2v2′, 這表明,只有當(dāng)二者碰撞后同速,即碰撞后粘在一起時(shí),系統(tǒng)損失的動(dòng)能最大. 點(diǎn)評:解題關(guān)鍵是掌握數(shù)學(xué)中的柯西不等式,利用數(shù)學(xué)知識解決物理問題,難點(diǎn)是把由物理量組成的多項(xiàng)式變換為符合柯西不等式的形式. 解法2:利用柯尼希定理.對于在光滑水平面上沿同一直線運(yùn)動(dòng)的兩個(gè)物體,由于系統(tǒng)受到的合外力為0,則系統(tǒng)的質(zhì)心做勻速直線運(yùn)動(dòng),那么質(zhì)心的動(dòng)能保持不變,根據(jù)柯尼希定理可知,碰撞后的動(dòng)能等于系統(tǒng)的質(zhì)心動(dòng)能與兩個(gè)物體的相對動(dòng)能之和,因此只有當(dāng)相對動(dòng)能為0時(shí),系統(tǒng)的動(dòng)能才最小,即系統(tǒng)損失的動(dòng)能最大,而此時(shí)相對速度為0,即發(fā)生了完全非彈性碰撞.所以說當(dāng)發(fā)生完全非彈性碰撞時(shí)系統(tǒng)損失的機(jī)械能最大. 綜上可見,利用柯尼希定理解答質(zhì)點(diǎn)系的相對速度問題不僅能化繁為簡,還可拓展解題思路,既有助于加深理解知識,又可訓(xùn)練思維能力,可謂一舉多得.

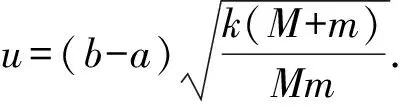
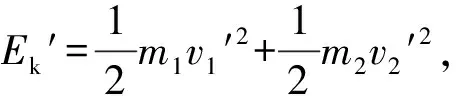
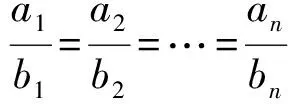


- 物理教師的其它文章
- 發(fā)展“科學(xué)思維”素養(yǎng)的探索與思考
——以“伽利略對自由落體運(yùn)動(dòng)的研究”教學(xué)為例 - STEM視野下中英物理教材對比
——以“動(dòng)量和動(dòng)量定理”為例 - 基于學(xué)生體驗(yàn)的“三步走”教學(xué)設(shè)計(jì)
——以“長度的測量”教學(xué)為例 - 初中物理科學(xué)探究教學(xué)中育人目標(biāo)和任務(wù)解析及實(shí)踐探索
- 物理實(shí)驗(yàn)?zāi)芰Ρ憩F(xiàn)標(biāo)準(zhǔn)的開發(fā)研究
- 基于BOPPPS教學(xué)模式的高效課堂教學(xué)設(shè)計(jì)
——以“伽利略對自由落體運(yùn)動(dòng)的研究”為例

