基于容錯決策樹的UWB輔助慣性定位方法

劉 宇，陳自然，顧洪洋，付樂樂，路永樂，李星海

(1.重慶郵電大學 智能傳感技術與微系統重慶市高校工程研究中心，重慶 400065；2. 中國電子科技集團公司第二十六研究所，重慶 400060)

0 引言

基于位置服務是現代生活里許多應用場景所需的關鍵特征，人們越來越依賴其帶來的便利性。在室外，GPS、北斗等得到了很好的探索和標準化，但由于其信號易受室內復雜環境的阻隔，導致無法在室內復雜環境實現高精度的定位[1]。因此，室內高精度定位研究具有很高的商用價值。

慣性導航系統利用載體自身的角速率和加速度進行實時測量解算姿態信息和相對位置信息[2]，具有成本低,體積小,無源等優點，在短期內對室內復雜環境能有效實現較高精度定位，但慣性導航系統隨著時間增長，陀螺和加速度計等慣性元器件本身產生的測量誤差等使其相對定位點出現較大誤差[3]，單一模式不適合長時間定位[4]。

為解決慣性導航存在的自身缺陷，在基于射頻(RF)的定位技術中，超寬帶(UWB)系統由于其具有高精度、低成本和低功耗，已經非常流行。與超聲波相比，紅外、藍牙、ZigBee、射頻識別技術和WIFI等有顯著優勢，雖然這些技術在一定程度上滿足了部分室內活動的需求[5]，但仍存在成本高，定位精度差等缺點。目前，國內外學者提出了采用UWB定位技術的多源信息對慣性導航進行輔助修正。Lukasz Zwirello等[6]提出了一個基于仿真的緊密UWB和慣性數據集成的可行性研究；Qigao Fan等[7]提出了利用雙態自適應卡爾曼濾波器的INS/UWB定位系統；曾慶化等[8]提出了基于零速修正的UWB優化配置室內行人導航。但多數學者未進行組合定位的相互容錯判定，在建筑結構復雜的室內環境中，UWB定位易受到非視距問題、多徑效應和人體的影響出現粗大誤差，可能導致慣性導航/UWB定位精度下降，甚至錯誤地輔助修正慣性導航。

本文提出了一種基于容錯決策樹的UWB定位信息輔助修正慣性定位的方法。首先提出并采用陀螺儀高精度分段擬合誤差補償模型，抑制慣性導航誤差漂移；同時將慣性導航解算的定位信息與UWB單點定位數據作為參考量共同構建容錯決策樹模型流程，有效剔除UWB粗大誤差，進而利用2個定位結果的參數進行擴展卡爾曼濾波，實現UWB輔助增強慣性定位，實現連續性可靠定位。

1 室內慣性導航定位系統解算

本系統采用嵌入式系統作為慣性導航定位系統硬件測試平臺，集成了多個慣性傳感器件。該定位系統首先進行慣性導航的初始加速度計/磁力計組合姿態解算；然后對慣性器件誤差校準，構建了陀螺儀高精度分段擬合誤差補償模型；根據載體自身的角速率和加速度進行實時、步數檢測和步長估計測量解算姿態信息和相對位置導航信息。

1.1 初始加速度計/磁力計組合姿態解算

本文采用地理坐標系即東北天坐標系(n系)，使用加速度解算的初始俯仰角、橫滾角，再加上磁力計進行共同解算，得到姿態角信息數據。設θ，γ，ψ分別為俯仰角、橫滾角和航向角，且

(1)

1.2 陀螺儀高精度分段擬合誤差補償

三軸陀螺儀用于采集姿態解算過程中所需要的角速度數據信息，其輸出值的精確程度直接影響到姿態數據精度。為了進一步減小誤差，分析了傳感器自身的安裝標定誤差、非線性誤差等，利用角速率輸出誤差模型，本文提出對陀螺儀進行高精度分段擬合誤差補償。角速率輸出誤差模型為

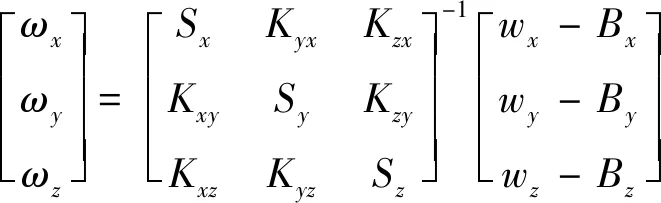
(2)

式中：ωx，ωy，ωz為陀螺儀真實角速率；Sx，Sz，Sy為陀螺儀標定因數；Kyx，Kzx，Kxy，Kzy，Kxz，Kyz為陀螺儀安裝誤差系數；Bx，By，Bz為陀螺儀零偏；wx，wy，wz為陀螺儀實際角速率測量值。

在高精度分段擬合誤差補償的實驗中，選取三軸轉臺動態速率為-100～100 (°)/s，以10 (°)/s作為間隔，共20個角速率，每組采集保留500 kbytes數據。按照速率數據正負對稱和動態速率高低，將20個角速率分為8組，在每個分段組中，以取三軸轉臺動態速率值為橫坐標，陀螺儀真實角速率為縱坐標，對其數據進行擬合，得到各軸該分段組標定因數Sx、Sz、Sy，安裝誤差Kyx、Kzx、Kxy、Kzy、Kxz、Kyz及零偏Bx、By、Bz。

以x軸為例,設置動態速率為-100 ～100 (°)/s，對x軸原始誤差和校準后誤差進行均值記錄(見表1)。

表1 陀螺儀高精度分段擬合誤差補償前、后對比表

由表1可知，經過高精度分段擬合誤差補償后，可區分補償高低動態速率段，更進一步消除角速率輸出誤差，減少了1～2個數量級。

1.3 四元數姿態解算

采用四元數算法對傳感器測量值進行姿態解算，利用慣性導航姿態解算的四元數參考值，實時計算出坐標矩陣，結合姿態轉換算法，即可解算出i時刻三軸θ、γ、ψ分別為

(3)

式中：q0為四元數的標量；q1、q2、q3為四元數的矢量。

1.4 步數檢測和步長估計

根據加速度特征數據仿真發現，行人走路的波峰、零點和波谷數據有似正弦波的周期性規律，利用漢明窗提取特征數據。但由于行走過程中身體存在抖動，加速度波形可能出現偽波峰，進一步消除其造成的步數誤判采用閾值判別法：

(4)

閾值范圍內，檢測到一個有效步數是以有效波峰值和有效波谷值為周期。經實驗驗證，人員行走108步，則檢測到的有效波峰為108個(見圖1)，此方法能準確檢測人員行走的步數。

圖1 加速度步數檢測圖

利用加速度與人員行走時刻步長的波峰、波谷差值之間的關聯性，采用下式進行自適應步長計算：

(5)

式中：j為行人的第j步；Lj為行人第j步的實時步長；K為行人步長標定參考值；amax,j、amin,j分別為第j步目標加速度最大波峰值、最小波谷值。

2 UWB定位系統解算

UWB定位是一種基于距離測量的室內高精度定位通信新技術，一定范圍內準確獲得人或物的位置和導航信息。本文的UWB定位測距通信模塊使用雙向飛行時間(TW-TOF)測量2個以上UWB模塊的間距，其可提供具有短脈沖的精確時間測量，同時保持對多徑信號傳播的魯棒性。

TW-TOF不要求通信雙方時間的同步性，自模塊運作后將擁有其獨立的時間戳,如圖2所示。

圖2 TW-TOF測距方法

首先分別得到模塊A、B的脈沖發送和接收時刻的傳遞時間Ta、Tb為

(6)

再利用無線電信號傳播的速度即光速c，可計算2個實體的距離p為

(7)

3 基于容錯決策樹的UWB輔助慣性定位

慣性導航系統對載體自身的角速率和加速度進行實時測量，解算得到姿態信息和相對位置導航信息后，利用UWB定位輔助增強室內定位精度，實現多傳感器多源定位信息下的連續性可靠定位。UWB設備的布設將針對不同的室內環境而定，在復雜狹窄巷道環境時，兩端布設UWB基站進行輔助；常規環境下，在同一樓層拐點或分叉口布設UWB基站進行輔助，合理減少室內環境中UWB基站數量。UWB所獲得的定位數據用于輔助修正慣性導航解算的定位信息，降低系統隨時間累積誤差。

3.1 UWB單點定位數據的容錯決策樹判定

在室內環境中，由于UWB定位存在易受遮擋物引起的非視距(NLOS)誤差及信號不穩定等多種影響定位精度情況，先行對UWB是否接收到多邊基站信號和出現粗大誤差進行有效判定，并將慣性導航解算的定位數據作為決策樹容錯判定的參考量共同構建模型流程。

在容錯判定開始前將當前k時刻的UWB單點定位數據作為輸入量。

首先進去到第一層容錯判定，需要獲知UWB標簽是否接收到定位基站的脈沖信號，則利用Tuwb標志位判定是否存在UWB單點定位數據,即

(8)

通過Tuwb標志位判定后，利用UWB單點定位數據獲得其標簽與定位基站之間的飛行時間后，使用TW-TOF測量標簽與各基站的定位距離，由式(7)可解算得距離p。

在通過TW-TOF法獲得標簽到多個定位基站的距離后，本文選用三邊測距定位法計算行人當前k時刻的移動位置最優解Puwb,k(xn,yn)：

(9)

式中:xn,yn分別為由n個UWB定位基站共同解算的標簽x、y軸移動位置最優解;pn為標簽到第n個定位基站的距離。

UWB定位基站的布設數量根據不同的室內環境而定，若行人處于復雜狹窄巷道環境中，行人將UWB標簽與慣性定位模塊集成一同放在腰間，可能出現無法接收3個及以上的基站時間戳的情況，則默認由TW-TOF得到的2個基站距離p1、p2計算位置信息；若行人處于常規方正室內環境，在房間4個拐點UWB基站進行輔助，則默認由TW-TOF得到的多個基站距離p1、p2、p3、p4計算二維位置信息。

通過第一層容錯判定，若不存在UWB單點定位數據，單邊基站所得到定位數據不具可信度，則不使用UWB輔助慣性導航解算。如果存在UWB單點定位數據，由于UWB數據存在粗大誤差在第一層容錯判定中無法完全消除，需結合慣性導航定位數據作為參考量,進一步提高可信度。

接下來進入第二層容錯判定，在復雜狹窄巷道環境時，根據行人運動規律特性，安放在人員腰間的定位模塊出現航向角度大幅變化時，UWB數據存在粗大誤差的幾率降低。故在此環境下，需要利用當前k時刻慣導解算對應的航向角ψk和初始航向角ψzero進行判斷行人是否發生轉彎模式變化。

(10)

式中：Δψ為k時刻航向角與初始航向角的差值絕對值；ε為判斷行人轉彎模式的活動閾值。

從第二層容錯判定中可看出，行人轉彎模式是對UWB粗大誤差的剔除，在確定轉彎判定能接收到基本精確的UWB單點定位數據后，需結合慣性導航解算的位置數據和行人步數進行判斷位置條件，進入第三層容錯判定。若不在復雜狹窄巷道環境下，直接進入第三層容錯判定。

根據在行走定位過程中的運動特性，佩戴人員在常規情況下，其前、后采樣點的位置不會突變，應該滿足UWB位置和慣性導航位置之間的距離差條件。并且隨著運動時間累積，其距離差值將會保持在合理范圍內。因此，采用同一采樣點的慣性導航與UWB定位信息差Δp進行測量數據的活動閾值判定，即

(11)

式中：Pins,k為慣性導航在k時刻的位置數據；Puwb,k為UWB在k時刻單點定位距離數據；σ為慣性導航與UWB位置數據之差的活動閾值。

考慮到隨時間累積后定位誤差的線性變化，若UWB和慣性導航解算位置差保持在合理的范圍內，允許其σ存在波動。由于在時域中無法將每一時刻與距離誤差一一對應，故使用行人運動步數與距離間的關系，其σ能同時滿足下列行走步數范圍的關系為

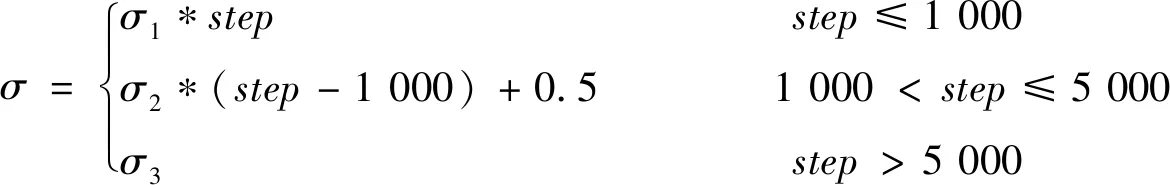
(12)

式中：step為加速度解算的有效步數；σ1，σ2，σ3為分段步數對應的閾值。

經過容錯決策樹的三層判定，最終實現了利用慣性導航解算的定位信息與UWB單點定位數據作為參考量，共同構建容錯決策樹模型流程，提高了定位精度。

3.2 基于擴展卡爾曼(EKF)濾波的慣性導航/UWB定位信息融合

通過UWB單點定位數據決策樹容錯判定后得到了當前時刻穩定的位置信息，將其作為觀測信息與慣性導航解算數據進行濾波，其狀態方程與觀測方程如下：

(13)

式中：k為離散時間所對應的時刻，系統在k時刻的狀態Xk∈Rn；Zk∈Rm為對應狀態的觀測信號；Φk為狀態轉移矩陣；Gk為狀態噪聲驅動矩陣;Wk∈Rn為輸入信號的白噪聲;φk為非隨機的外作用項;Hk為觀測矩陣;Vk∈Rm為觀測信號的白噪聲。

設計X=[δp,δv,δφ,δa]T為該EKF濾波的狀態向量，包含12個狀態量，其中行人的位置誤差δp(δpx、δpy、δpz)、慣性導航東、北、天坐標的速度誤差δv(δvE、δvN、δvU)、當前時刻慣性導航所解算的姿態角誤差δφ(δφγ、δφθ、δφψ)以及三軸加速度誤差δa(δax、δay、δaz)作為狀態向量，E、N、U分別為東、北、天坐標系中的東向、北向和天向位置。

針對姿態角誤差補償，當初始時刻檢測到開機站立時，默認此時慣性導航解算的姿態角為初始姿態角。將慣性導航解算的實際姿態角與初始姿態角之差Δψ作為當前時刻姿態角的觀測量。針對位置誤差補償，使用慣性導航與UWB解算的位置信息之差作為當前時刻位置的觀測量Δp。觀測向量Z=[Δp,Δψ]。其中：

(14)

式中wΔp，wΔψ為對應觀測量的觀測模型噪聲。在這個過程中，假設wΔp，wΔψ相互獨立且滿足高斯白噪聲。首先對狀態方程進行求導可得Φk為12×12的狀態轉移矩陣，即

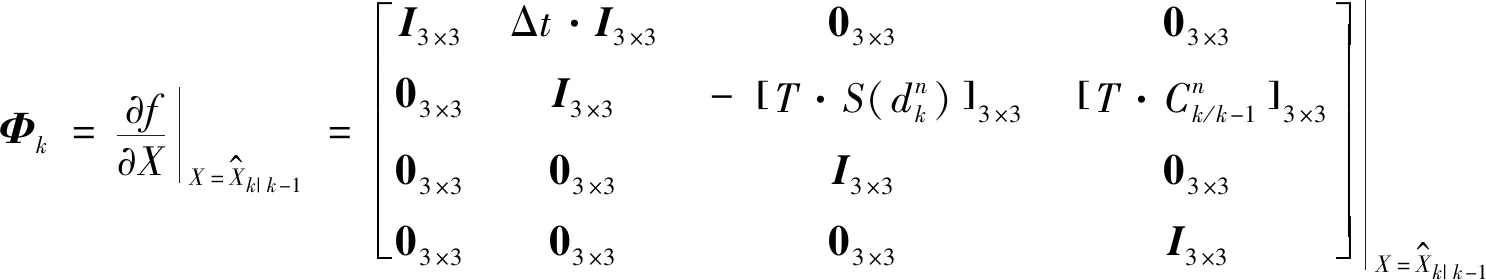
(15)

Hk為觀測量的轉換矩陣，且

(16)

4 實驗驗證與分析

為了驗證本文提出的基于容錯決策樹的UWB輔助慣性導航解算可靠性，將UWB標簽與慣性定位模塊集成，佩戴在行人后背的腰間(見圖3)，以便在行走過程獲得更穩定的位置數據。實驗中慣性定位采用集成了三軸陀螺儀、三軸加速度計、三軸磁力計等傳感器的嵌入式微系統作為硬件平臺，通過傳感器數據實時解算行人的位置和航向；UWB使用定位測距通信模塊，定位基站的布設根據不同的室內環境而定。定位系統的上位機實時接收慣性導航和容錯判定后的UWB解算定位數據，再利用EKF濾波對定位信息融合。

圖3 慣性定位模塊和UWB裝置

本文分別在兩種不同環境下進行實驗，以證明基于容錯決策樹的UWB輔助人員室內定位在復雜和常規環境均有效。第一種實驗在復雜狹窄巷道環境中，驗證能否準確進入到對應的房間；第二種實驗在常規方正室內環境，軌跡類似于矩形，驗證系統的可靠性。由于UWB信號通常無法穿過建筑物的混凝土墻，這導致大量的信號延遲，故本實驗不考慮高度問題，在2D平面進行定位。

4.1 復雜狹窄巷道環境

設定實驗環境在重慶郵電大學第一教學樓(見圖4)，激光測距可得其直線過道長為33.23 m。該過道配備有2個UWB接入點，分別置于左、右兩端AP1(0,0)、AP2(0,33.23)，在圖中用▲表示。為了更好地對比純慣性導航解算和UWB輔助的定位系統精度，選取5個教學房間，規定統一的行走路線：起點AP1→房間①→房間②→房間③→房間④→房間⑤。行人出發航向由初始加速度計/磁力計組合姿態解算ψzero，二維坐標為(0,0)，并規定行人結束時方向與出發時一致。

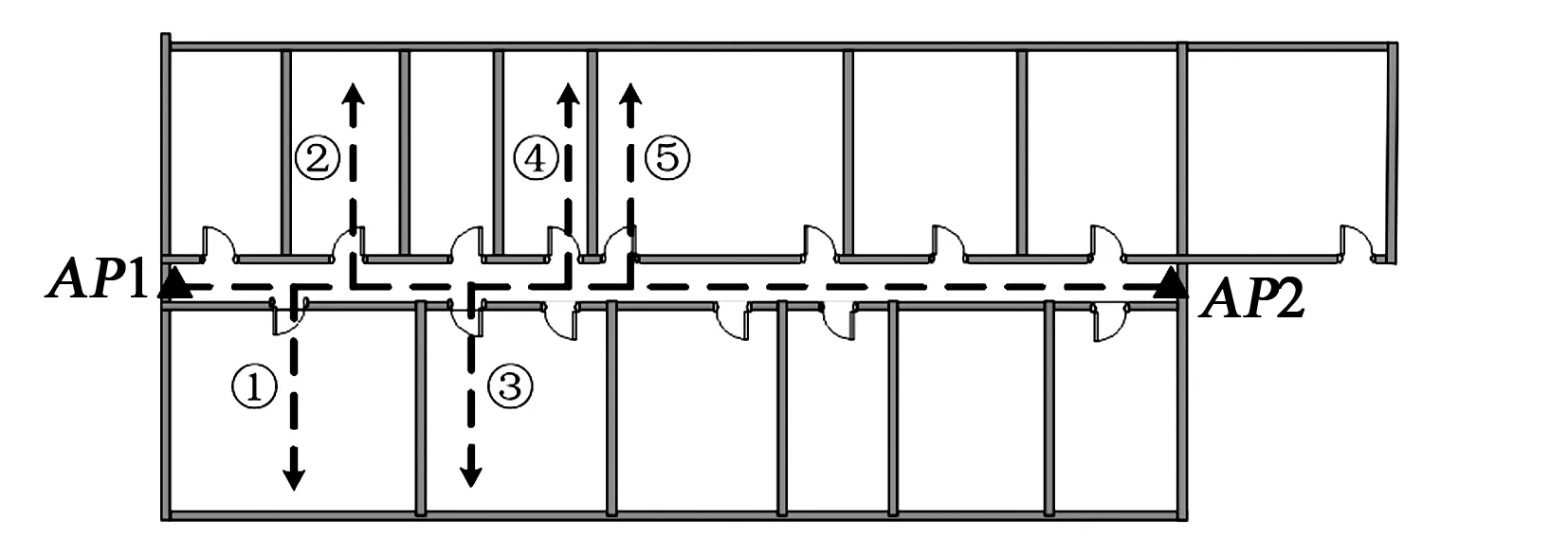
圖4 第一教學樓建筑結構圖及行走路線

圖5(a)為行人在過道及進入教學房間過程中，純慣性導航和慣性導航/UWB輔助定位的上位機行走界面。圖5(b)為實驗效果對比仿真圖。

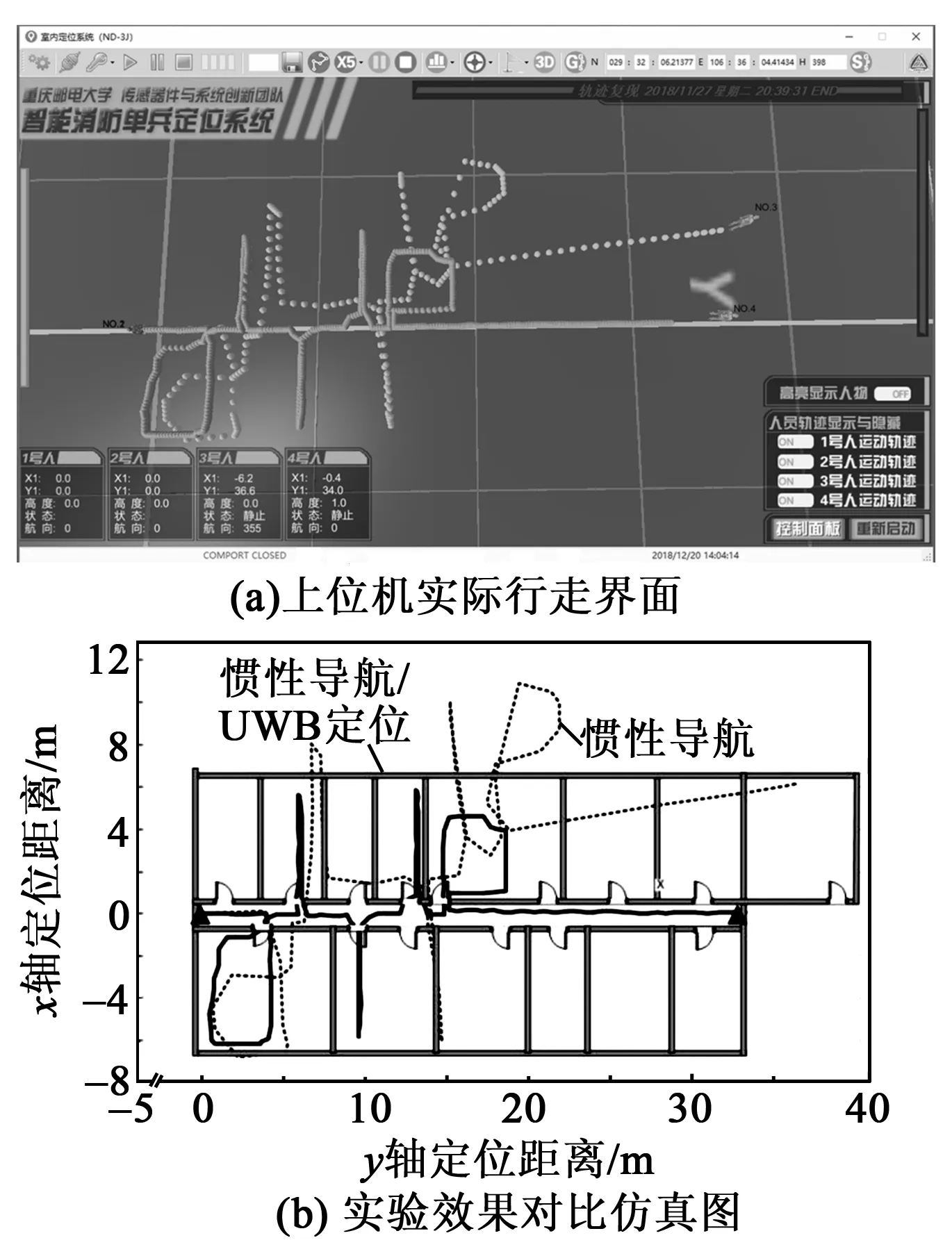
圖5 上位機實際行走及實驗效果對比仿真圖

圖5中行走路線的理論起點、終點分別為AP1(0,0)、AP2(0,33.23)，通過實驗對比分析，復雜狹窄巷道環境下，在無UWB輔助的純慣性導航時，位置和航向角逐漸偏離真實定位軌跡，且隨著時間的增長，其相對定位點出現較大誤差，呈現連續變化特性。

由圖5(b)可看出，當行人進入到房間時，有效的UWB測量單點定位信息輔助修正慣性導航，將行走軌跡拉回到正確的區域，無UWB輔助修正的慣性導航定位無法解算原始軌跡現。當行人到達理論終點AP2時，純慣性導航解算點為A(6.2，36.56)，慣性導航/UWB定位解算點為B(0.39，34.03)，實際行走距離長度為116.86 m。根據數據計算可得，A點到起點的均方位置差為7.038 m，距離均方誤差占路線長度的6.02%；B點到起點的均方位置差為0.89 m，距離均方誤差占路線長度的0.76%。

4.2 常規方正室內環境

設定實驗環境在重慶郵電大學第七教學樓,室內配備4個UWB定位基站(見圖6)，均安裝在房間的拐角處天花板墻上。UWB定位基站坐標由激光測距儀得到，分別為AP1(0,0)、AP2(0,39.5)、AP3(18.5,39.5)、AP4(18.5,0)，在圖中用▲表示。實驗統一的行走路線為從起點AP1沿逆時針方向，分別經過AP2、AP3、AP4，繞行兩圈回到起點AP1。行人出發航向由初始加速度計/磁力計組合姿態解算ψzero，并規定行人結束時方向與出發時一致。

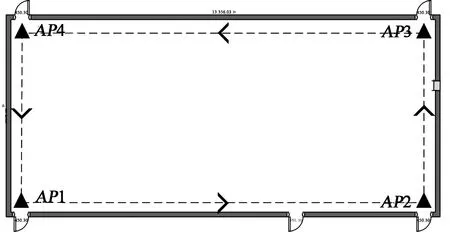
圖6 第七教學樓建筑結構圖及行走路線

圖7為行走路線的純慣性導航和慣性導航/UWB輔助定位的實驗效果對比仿真圖。由圖可以看出，純慣性導航定位路線隨著時間累積誤差，在第二圈時出現了較大的位置漂移；慣性導航/UWB定位路線有效剔除了UWB粗大誤差定位信息，并快速輔助修正慣性導航長時間連續定位的誤差，與實驗規劃路線吻合較好。當行人繞行兩圈回到AP1時，純慣性導航解算點為A(0.542，1.294)，慣性導航/UWB定位解算點為B(-0.124，-0.061)，實際行走距離為232 m。由于實際行走軌跡為常規方正矩形，存在各個方向漂移相互抵消，故不只限于分析終點誤差值。純慣性導航的距離誤差為-1.38～5.12 m，最大誤差占路線長度的2.207%；慣性導航/UWB定位的距離誤差范圍為-1.473 8～0.160 3 m，最大誤差占路線長度的0.635%。

圖7 實驗效果對比仿真圖

綜上所述可知，與純慣性導航相比，在復雜狹窄巷道和常規方正室內環境下，慣性導航/UWB定位系統人員行走真實路徑與規劃路徑更貼合，顯著降低了定位誤差，有效抑制誤差隨時間累積漂移，實現了多傳感器多源定位信息下的連續性可靠定位。

5 結束語

本文針對慣性導航系統誤差隨時間累積和UWB定位受到非視距問題、多徑效應和人體影響出現粗大誤差的問題，提出了一種基于容錯決策樹的UWB輔助慣性定位方法。該方法采用陀螺儀高精度分段擬合誤差補償模型，抑制慣性導航誤差漂移；同時構建UWB單點定位數據的容錯決策樹判定，剔除粗大誤差因子，進而使用慣性導航和UWB參數進行擴展卡爾曼濾波，實現UWB輔助增強慣性導航定位。

實驗中慣性定位采用集成了三軸陀螺儀、三軸加速度計、三軸磁力計等傳感器的嵌入式微系統作為硬件平臺；UWB使用定位測距通信模塊，定位基站的布設根據不同的室內環境而定。根據實驗平臺對兩種不同環境進行實驗驗證。在復雜狹窄巷道環境，本算法將距離均方誤差占路線長度的比例從6.02%提升到0.76%；在常規方正室內環境，本算法將最大誤差占路線長度的比例從2.207%提升到0.635%。實現了長時間的連續可靠定位，具有很強的工程應用價值。