低溫液體運載火箭變形補償量設計及試驗方法

李 東，馮韶偉，王 月，吳 潔，鄭明珠

（1. 北京航空航天大學宇航學院，北京，100191；2. 中國運載火箭技術研究院，北京，100076； 3. 北京宇航系統工程研究所，北京，100076；4. 北京航天計量測試技術研究所，北京，100076）

0 引 言

隨著國際空間組織對發射場、落區環境的要求，以液氫-液氧作為推進劑的無毒、無污染的液體運載火箭成為世界各國關注和研發的重點。液氫-液氧是目前液體運載火箭中比沖最高的實用型推進劑組合[1]。然而這種推進劑的溫度極低，會在加注、增壓過程中造成箭體結構的變形，從而對箭體結構和管路系統設計的補償量提出更高的要求。

為了計算貯箱在工作過程中的變形量，在工程中通常采用有限元計算方法，該方法能夠有效模擬貯箱在增壓、加注以及飛行過程中不同載荷條件下箭體結構的變形量，計算結果直觀。但有限元方法的計算規模較大造成分析效率較低，難以模擬線膨脹系數隨溫度的變化規律，且該方法對建模與實物的相符程度要求較高，否則會造成結果失真。

在傳統的運載火箭研究過程中，缺少有效的低溫加注后變形量系統的試驗檢測方法，造成試驗難以覆蓋設計，以及試驗結果的外推性不強的難題。

針對運載火箭貯箱的結構特點，本文提出一種低溫火箭變形量解析設計方法，獲得貯箱在低溫、增壓作用下的變形量，并基于平面視覺測量原理對試驗中的貯箱變形量進行檢測，通過與有限元方法及試驗結果的對比，驗證解析方法的合理性，從而為低溫液體運載火箭變形補償量的設計提供參考和依據。

1 貯箱變形量解析方法

1.1 溫度載荷

靜定結構在各處均勻的溫度載荷作用下，模型各個部件間連接處的位移連續且不會產生應力。由模型的邊界條件可認為模型形狀將不發生變化，各幾何尺寸發生相同比例的伸縮[2]。因此可以認為，在低溫液體加注之后，所有區域都由初始溫度T0變化到T1，對于長度為l 的貯箱，由溫度變化產生的位移δ 為

式中α 為貯箱的材料線膨脹系數，表示溫度每變化 1 ℃，材料長度變化的百分比[3]。對于固體物質來說，表示溫度每改變1 ℃時，其長度的變化與其在0 ℃時長度的比值。

假設所研究貯箱的材料為5A06 鋁合金，其線膨脹系數隨溫度的變化曲線如圖1 所示。因此，對于工作溫度的線膨脹系數，應進行差值選取，本文采用3 次拉格朗日差值法。

貯箱在各處均勻的溫度載荷作用下，各個部件間的連接處的位移連續且不會產生應力，各幾何尺寸發生相同比例的伸縮。由初始溫度T0變化到T1后，貯箱體積V 變為

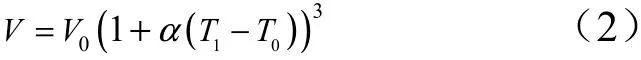
1.2 內壓載荷

在內壓載荷下，將貯箱（高度為H，半徑為r）筒段及前、后底分開考慮，假設貯箱的壁厚為d。在箱筒段處，由平衡方程貯箱箱筒段在內壓P 的作用下的軸向應力 σ1和徑向應力 σ2分別為

由物理方程可以得到貯箱箱筒段的軸向應變1ε 和徑向應變2ε 為

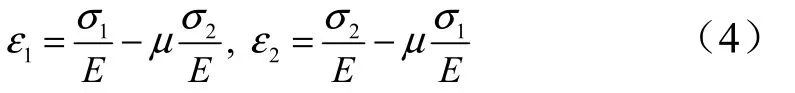
式中E，μ分別為材料的彈性模量和泊松比。

由此可以得到柱段高度變化量和柱段半徑變化量分別為

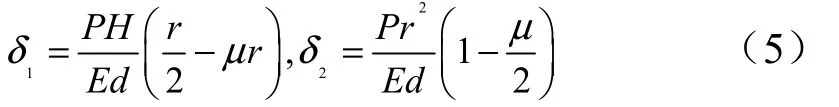
對于前后底，在相同內壓的作用下，結構的應力表達式為

同理，可以推導貯箱前后底的變形為

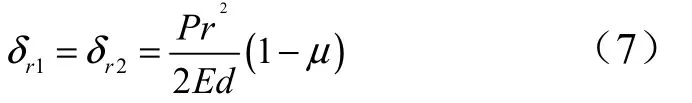
從式（5）和式（7）可以看出，圓筒和半球形封頭將在連續處產生不連續位移，不連續量為

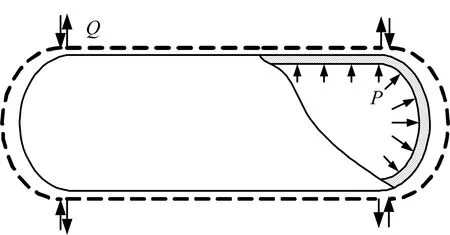
圖2 貯箱內壓載荷下變形示意 Fig.2 Deformation of the Tank under the Internal Pressure

在實際結構中，這種位移不連續現象是不允許的，因此在半球形封頭和圓柱段連接處必然存在圓周均勻分布的剪力 Q，而且其大小恰好消除這種不連續位 移[4]。封頭區因為上述原因產生的彎曲應力只對該區域附近有較大影響，所以可以將這一區域當成無限長柱筒的一部分來處理。在算例中，圓筒和封頭的厚度相同，在這種情況下可以認為彎矩很小，僅橫向剪力Q就使該部分產生相等的變形。根據圓柱殼體的軸對稱理論可得：

1.3 軸壓載荷

貯箱在前底與筒段連接位置受到軸壓F的作用時，對于貯箱筒段來說，其軸向應力1σ 和徑向應力2σ 分別為

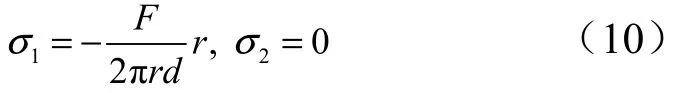
軸向應變 ε1和徑向應變ε2為

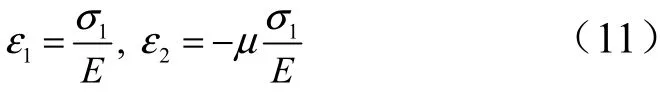
箱筒段的半徑變化量 δr為

而由于貯箱前后底與筒段連接位置的變形量為0，同樣會產生由于均勻分布剪力引起的不連續量。因此，

同理，圓筒段在連接區域因為剪力Q 引起向內擾度，然而，對應的有相同的剪力Q 將引起球形底向外的撓度，因此由剪力引起的撓度不會導致總體容積的變化。

2 解析方法驗證

為驗證解析方法的正確性，首先建立如圖3 所示的半球形底貯箱的有限元模型。模型半徑 r 為2500.0 mm，箱高H 為5000.0 mm，模型各處的厚度d均為5.0 mm，初始溫度為15 ℃。有限元模型采用四節點減縮積分殼單元。有限元模型的單元基本尺寸為40 mm。整體模型總計單元約為31 000，節點約為30 000。固支模型筒段與后底連接位置。

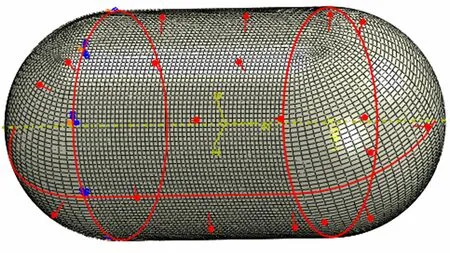
圖3 半球形底貯箱的有限元模型 Fig.3 The FEM of the Hemispheric Tank

有限元數值解與解析解法的對比情況如表1所示。

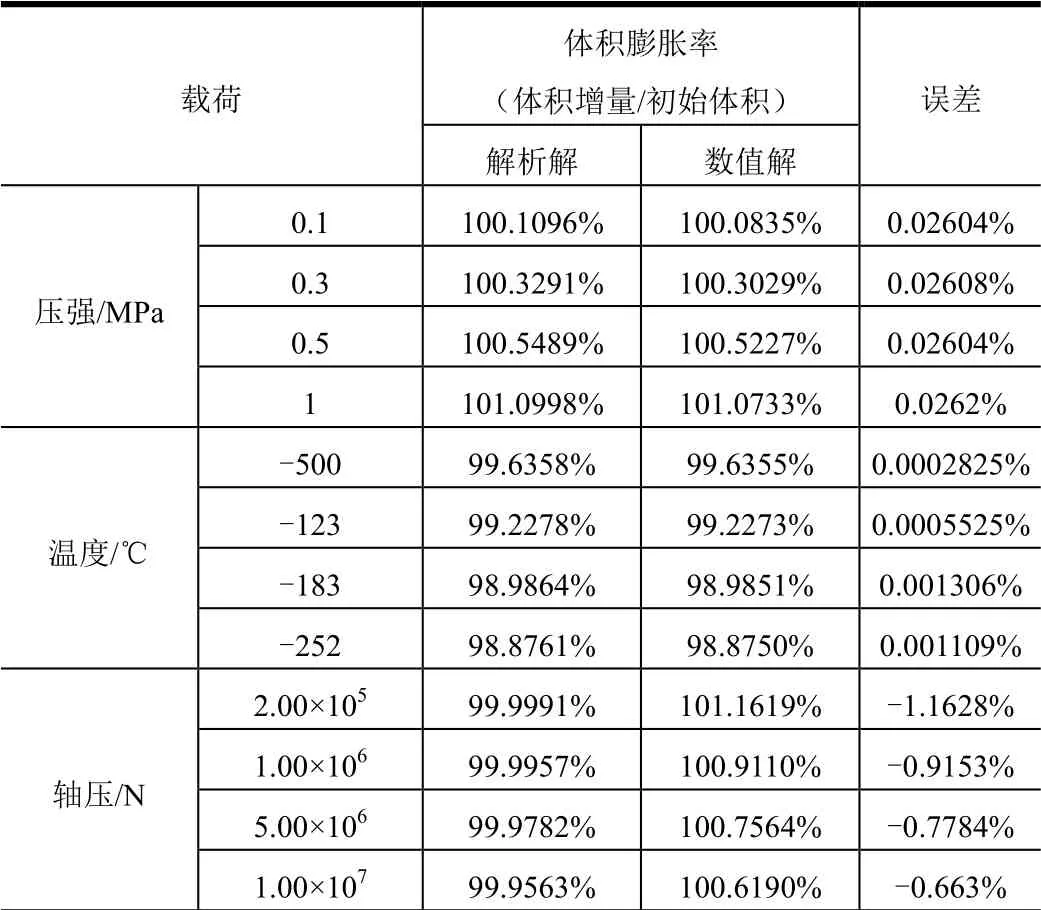
表1 數值解與解析解結果對比 Tab.1 The Comparision between the Numerical Method and the Analytical Method

由表1 結果可見，在溫度載荷作用下，解析解和數值解之間的誤差小于6×10-4%；在壓強作用下，數值解和解析解的所得結果誤差在0.03%以下；軸壓作用下，數值解和解析解的所得結果誤差在1.5%左右。而從量級上看，壓強與溫度是貯箱變形的主要因素，因此解析解有效、可靠。

3 測量方法

3.1 平面視覺測量原理

空間一點經過成像系統后，與圖像坐標系存在一組映射關系，當不考慮景深方向只考慮平面成像關系時，物空間平面物點與像空間成像點存在唯一的映射關系，這種映射關系由相機圖像傳感器參數和鏡頭參數唯一確定[5]。平面視覺測量原理如圖4 所示。

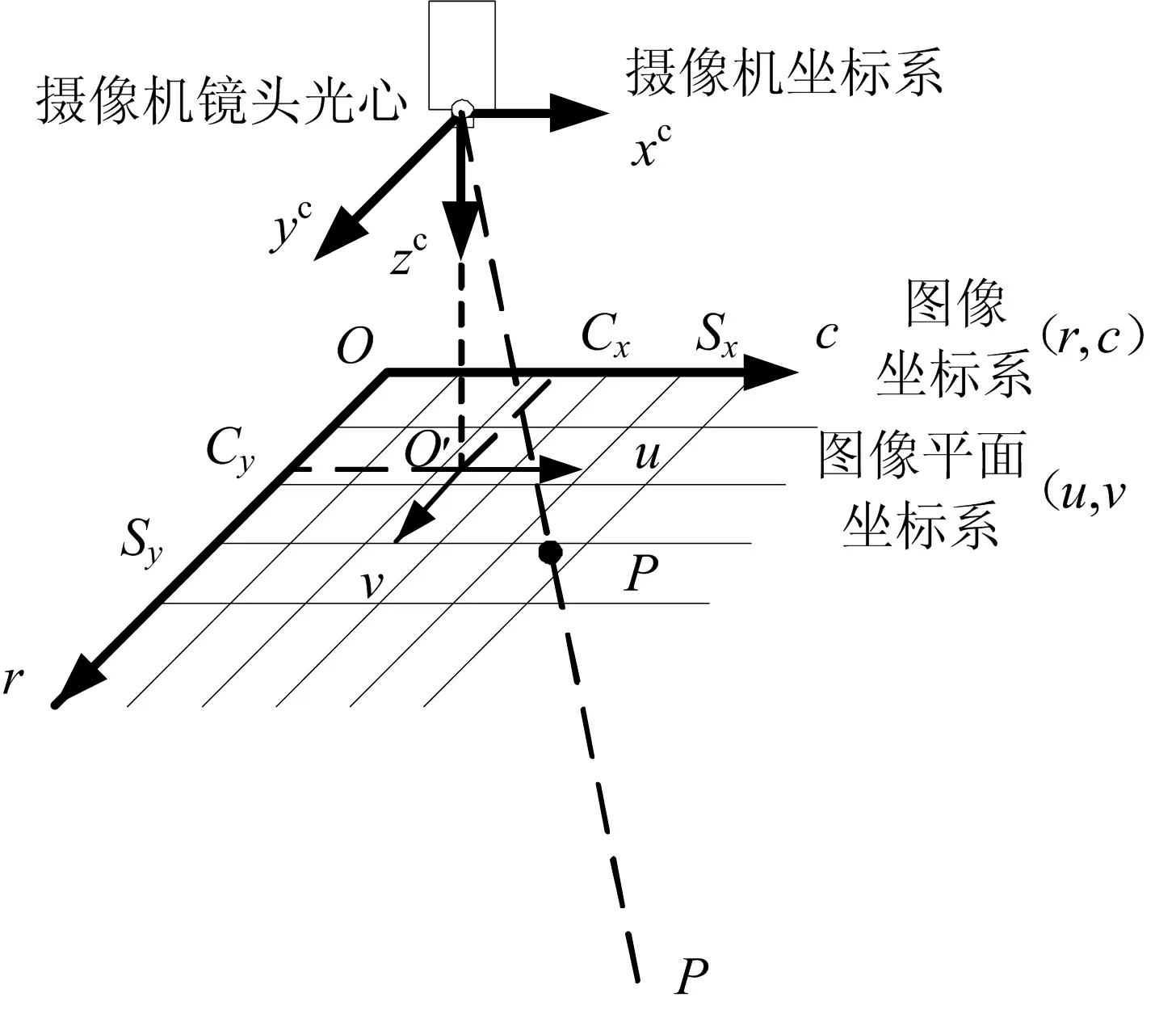
圖4 平面視覺測量原理 Fig.4 Schematic Diagram of the Graphic Vision Measurement Principle

在圖4 所示的測量原理圖中，相機的坐標系為xcyczc，其中 xc、 yc分別與相機圖像傳感器的行和列平行， zc與相機光軸平行。假設相機成像為小孔成像，經過三角變換后得到虛擬圖像坐標為uO 'v。

平面單目視覺測量就是對相機圖像傳感器參數和鏡頭參數進行標定。包括相機圖像傳感器當量因子標定，相機主點位置標定和相機物距標定等方面，上述參數標定涉及到式（14）的旋轉矩陣變換和式（15）的縮放矩陣變換：

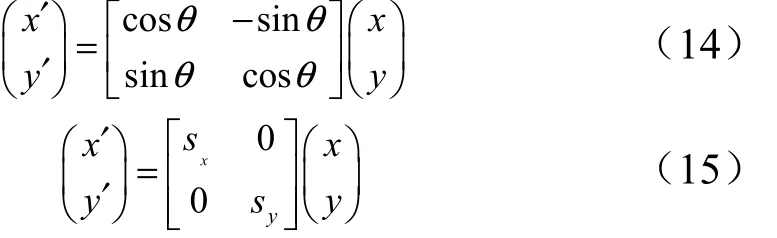
3.2 視覺畸變的非線性校正

在計算機視覺領域中，攝像機的線性模型是針孔模型，但實際的鏡頭并不是理想的透視成像，且帶有不同程度的畸變，使空間點所稱的像并不在線性模型所描述的位置。在上述的矩陣變換中均不含有鏡頭畸變因素，需要增加非線性畸變項xδ 和yδ ，即：

相機的視覺畸變分為3 種情況，分別為徑向畸變、離心畸變和薄棱鏡畸變[6]。研究表明，引入過多的非線性參數往往無法提高測量的精度，因此一般情況下，徑向畸變就足夠描述非線性畸變。

徑向畸變能夠使圖像點相對理想位置發生向內或向外的偏移，又稱為對稱的徑向失真[7]，如圖5 所示。

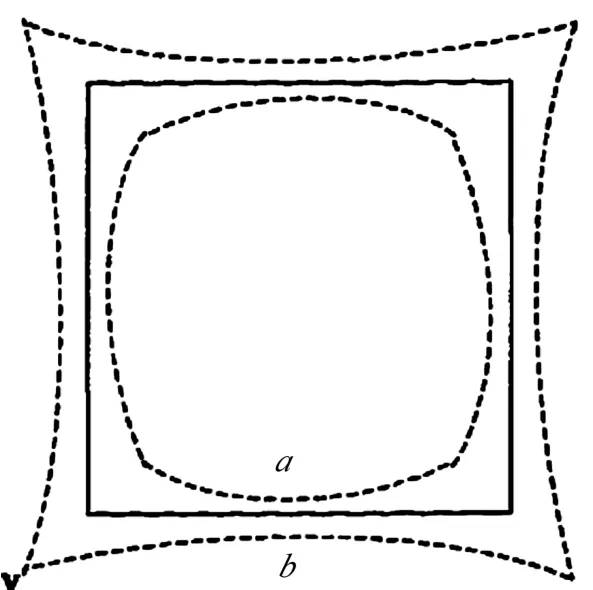
圖5 徑向畸變模型 Fig.5 Distortion Model in the Radial Direction

這種畸變主要是由于光學系統的鏡頭徑向曲率變化引起的，有正負兩種偏移效應，分別稱為桶形畸變和枕形畸變。由于徑向畸變相對于光軸是對稱的，在忽略高階項的情況下，靶標形心像面偏移量可表達為

式中kl為鏡頭的徑向畸變率。

4 貯箱變形量測量試驗

在某運載火箭試車過程中，基于平面視覺原理開展了變形量測量試驗。運載火箭推進劑貯箱自上而下分別為氧箱和氫箱，分別布置多個變形量測點。某截面上，變形量測量曲線如圖6 所示。測量結果與解析計算結果進行對比，結果如表2 所示。

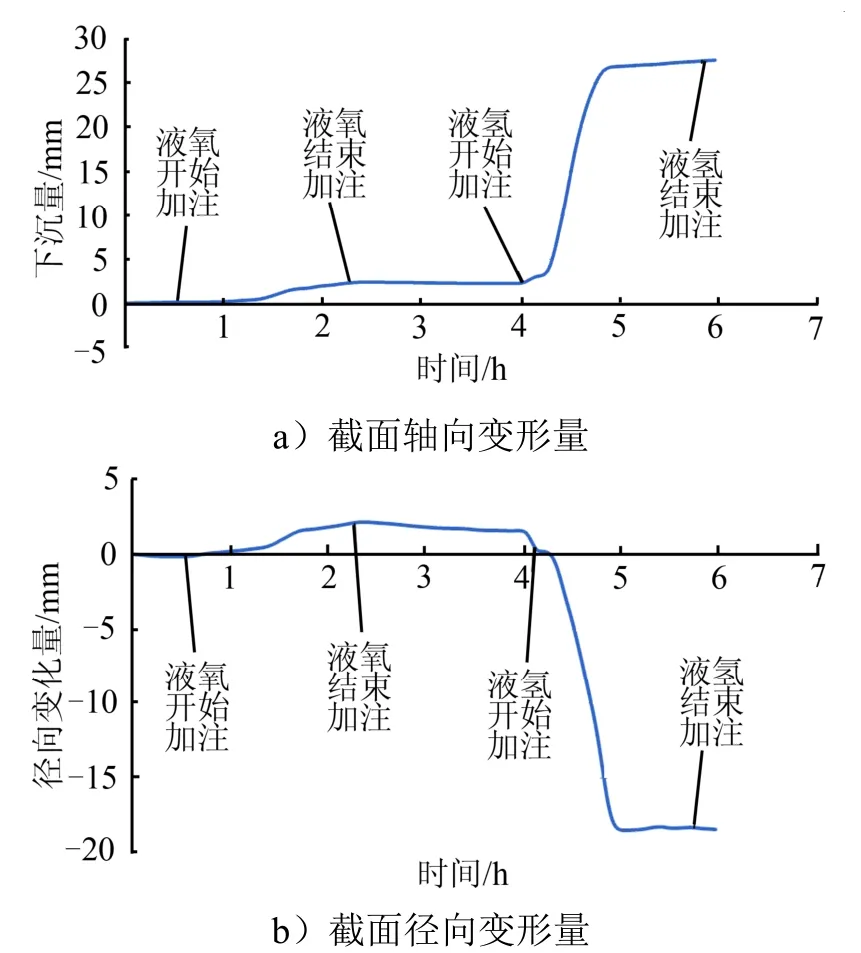
圖6 截面變形量測量結果 Fig.6 Measurement Result of One Section

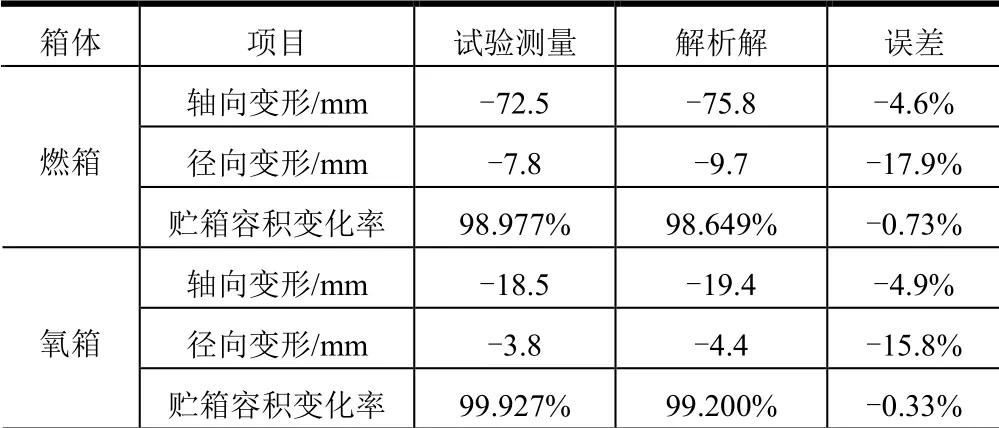
表2 貯箱變形量結果對比 Tab.2 Comparision Result of the Tank Deformation

由表2 可知，理論計算與試驗測量結果的一致性較好，在軸向方向上兩者誤差在5%以內，徑向方向誤差控制在2 mm 以內，且計算變形量均偏大，對于工程研制來說更加可靠。

另外，兩者軸向變形量更加接近，由于管路的補償量設計更加關注箭體軸向[8]，因此本文的理論計算方法能夠作為補償量設計的依據。

5 結 論

低溫運載火箭加注后的變形補償量設計是箭體結構和管路系統設計的關鍵輸入條件，其合理性直接關系到飛行任務的成敗。本文通過理論方法對半球形底貯箱的變形量進行了研究，并基于平面視覺原理研究大尺寸運載火箭的變形量測量方法，通過結果對比分析，驗證了理論方法和測量手段的合理、有效性，主要結論如下：

a）線膨脹系數與結構溫度有關，應選擇合理的插值方式進行選取；

b）壓強與溫度是低溫貯箱變形的主要因素，本文提出的解析方法與數值結果一致性較好，其中溫度載荷的誤差小于6×10-4%，壓強載荷的在0.03%以下，因此能夠在滿足工程研制需要的前提下，提高計算效率；

c）平面視覺原理測量需要考慮非線性畸變因素，而其中的徑向畸變是最為關鍵的設計因素；

d）通過對某型號運載火箭測量結果與理論計算結果的對比表明，在軸向方向上兩者誤差在5%以內，徑向方向誤差控制在2 mm 以內，且均以計算變形量偏大。鑒于管路的補償量設計更關注箭體軸向變形，因此本文的理論方法能夠作為運載火箭補償量的設計依據。