基于RBF 的替代模型在翼型穩健設計中的應用

蔡文杰，黃 俊，畢國堂，劉志勤，黎茂鋒

（西南科技大學，綿陽，621000）

0 引 言

近年來，隨著中國航空航天技術的大力發展以及民用大型客機研發需求的越發迫切，飛行器的穩健設計已經成為國防和民用科技發展關注的重點。機翼是飛行器整體設計中的重要一環，而翼型的選取又是機翼設計的重點。翼型的穩健設計能使飛行器在不斷變化的環境中使其性能保持穩定，如使其阻力保證在一個較低的水平，實現飛行又穩又遠的目標。

傳統的翼型設計是在一個人為設定的環境下進行的。但現實中的環境卻是時刻處于變化中，通過傳統方式獲得的翼型的性能可能會出現劇烈的波動。以馬赫數下的飛行器阻力優化為例，Hicks 等[1]對翼型的研究證明了對單一點馬赫數處的阻力進行優化的傳統單點設計方法，將會引起其附近馬赫數處的阻力變大，進而影響最終的翼型性能。而在更寬速度范圍飛行器的設計中該問題更加突出。通過對翼型進行穩健優化設計[2]能夠很好地解決此類問題，使飛行器翼型對環境變化不敏感。

1 翼型穩健設計簡要概述

翼型穩健設計就是要使翼型對外界環境變化帶來的噪聲因素不敏感。因此在翼型設計之初就要考慮到可能存在的噪聲因素，通過穩健設計最終尋找到一組可控因素的最佳水平組合，從而使噪聲因素對翼型性能的影響降低。

飛行器翼型在非設計狀態下的性能不穩定問題的解決方法通常就是進行翼型的穩健設計。翼型穩健設計就是要在一個給定的馬赫數變化區間（Mamin≤Ma ≤Mamax）中，實現不但要減小翼型的阻力而且還要保證翼型的性能穩定的目的。即要實現同時減小阻力系數的均值和方差的目的，本文中所采用的穩健設計目標模型[3,4]如下：

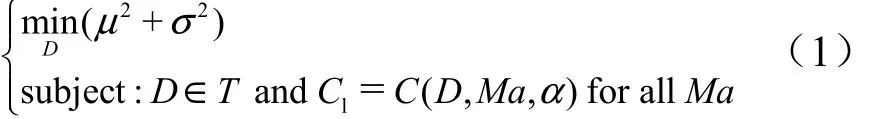
式中D 為多維翼型的幾何外形參數，即翼型外型設計變量；lC 為翼型設計中作為約束條件的升力系數；T為翼型的外型幾何約束；Ma 為設計中所選取的馬赫數；α為攻角；μ為期望；2σ 為方差。

在設計中，阻力系數和升力系數都是攻角、設計變量以及馬赫數的函數。在求阻力系數的過程中，為保證升力系數不影響結果，將其作為設計過程中的一個約束條件，可通過對攻角的調節來達到升力系數的恒定。

式（1）中的阻力系數 Cd的均值μ和方差 σ2的定義如下：

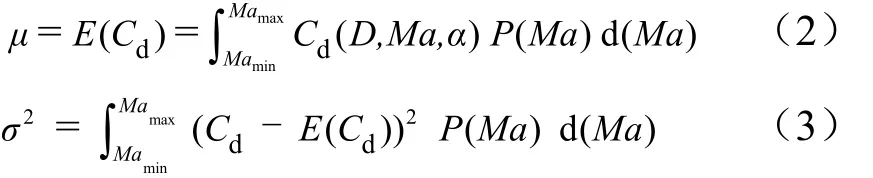
式中P(Ma)為Ma 的概率密度函數。

本文所進行的翼型穩健設計其目的是在一段給定的馬赫數變化范圍內，通過設計來減小翼型阻力系數的均值以及方差，來獲取穩健翼型。由于求解 Cd的計算量非常龐大，因而μ與 σ2的計算更加困難。因此本文采用通過建立 Cd關于翼型表面參數D 和馬赫數Ma 的2 種RBF 替代模型（插值和擬合），來進行 Cd的預測，使用預測的結果得到 μ2+ σ2的近似值,即:

與傳統直接通過CFD 計算阻力系數相比，替代模型的計算量明顯減少，且能滿足一定的設計精度要求。

2 翼型穩健設計流程

本文所采用的通過RBF 替代模型進行翼型穩健設計方法的流程圖與步驟如下（如圖1 所示）：

a）進行翼型外形的幾何參數化表示；

b）選擇試驗設計方法，確定試驗設計因素及其水平數，即生成樣本點；

c）對樣本點進行CFD 計算，獲得樣本點翼型在滿足升力約束條件下的阻力系數dC ；

d）根據獲得的樣本結果數據建立RBF 替代模型；

e）通過遺傳算法進行優化，獲取最佳翼型外形的設計參數值；

f）計算最佳翼型阻力系數的均值與方差，與基準翼型進行對比驗證。

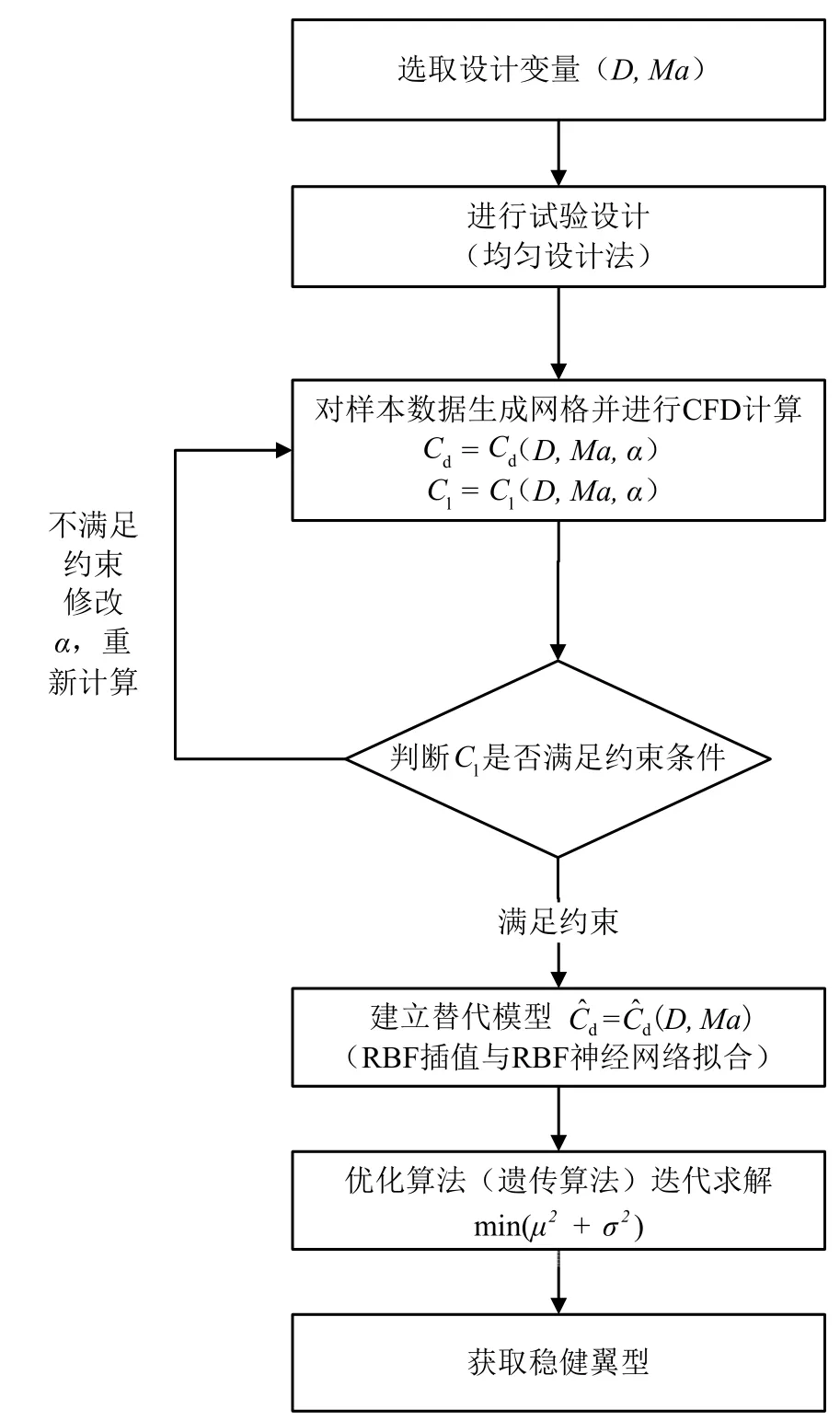
圖1 翼型穩健設計流程 Fig.1 Airfoil Robust Design Flow Chart

2.1 翼型外型參數化

本文采用Hicks-Henn[5]基函數線性疊加的方式來表示翼型外型，翼型形狀由基準翼型（本文選擇RAE2822 翼型）和基函數以及相關系數進行定義：

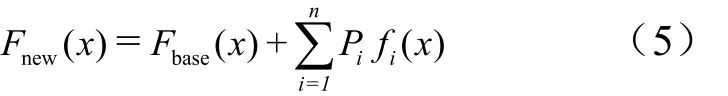
式中baseF 為基準翼型形狀；iP 為型函數的相關系數，即外型參數設計變量；n 為設計變量的個數；if (x)為Hicks-Henne 基函數。其中Hick-Henne 基函數的具體形式如下：

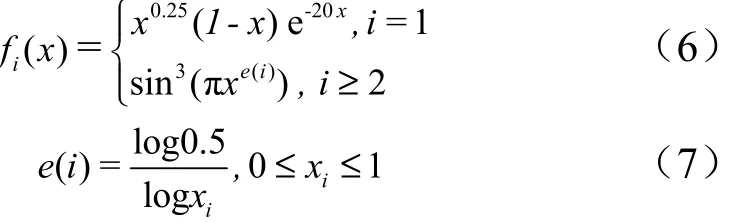
式中xi為翼型前緣點和后緣點間的結點，0= x1＜ x2＜… xi＜ xn=1。本文中xi=，i=2,…,5。

2.2 試驗設計方法

試驗設計方法是用來進行樣本點合理選擇的方法。本文選用均勻設計法來進行樣本點的選取。均勻設計法去除了正交設計中整齊可比的要求，其試驗點具有更好的均勻性，能充分反映試驗設計變量的信息。通過因素（變量）數及其水平數選擇合適的均勻設計表，生成樣本數據表。

2.3 網格生成與CFD 計算

在進行CFD 計算前，需要先對生成的均勻設計表中的每一個翼型樣例生成其對應的二維網格，該步驟通過網格生成軟件Gridgen 完成，網格采用C 型結構，網格生成結果如圖2 所示。后續氣動系數的計算可采用廣泛使用的CFD 軟件Fluent 完成，湍流模型選用Spalart-Allmaras，翼型壁面設置為Temperature。CFD的相關內容可參考文獻[6]，Fluent 的相關設置可參考文獻[7]。

生成網格后，本文使用Ma =0.73，α=o3.19 ，Re=6.5×106時RAE2822 翼型的fluent 表面壓力分析結果對網格和氣動分析結果進行檢驗見圖3，由圖3 可知，CFD 計算結果與試驗報告[8]中的試驗結果基本吻合，驗證了網格和氣動分析的正確性。

圖2 RAE2822 翼型的C 型網格 Fig.2 C-Grid for the RAE2822 Airfoil

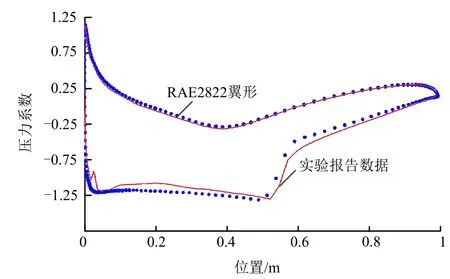
圖3 RAE2822 翼型表面壓力分布CFD 結果與試驗結果對比 Fig.3 Comparison of CFD Results of RAE2822 Airfoil Surface Pressure Distribution and Experimental Results

2.4 RBF 替代模型

本文采用與RBF 徑向基函數相關的2 種方法進行替代模型的建立，分別是：RBF 插值法和RBF 神經網絡擬合法。2 種方法的定義如下：

2.4.1 RBF 插值替代模型原理

RBF 插值是通過一系列的徑向基函數的線性組合來建立替代模型。其定義如下：

式中 φ(||x-ix ||)為徑向基函數，通常可采用高斯函數或多二次函數等，本文中后續RBF 插值替代模型采用高斯徑向基函數。

2.4.2 RBF 神經網絡擬合替代模型原理

RBF 神經網絡是在BP 神經網絡基礎上改進而來的一種神經網絡模型，是一種由輸入層、隱含層、輸出層構成的3 層結構的前饋型神經網絡，如圖4 所示。

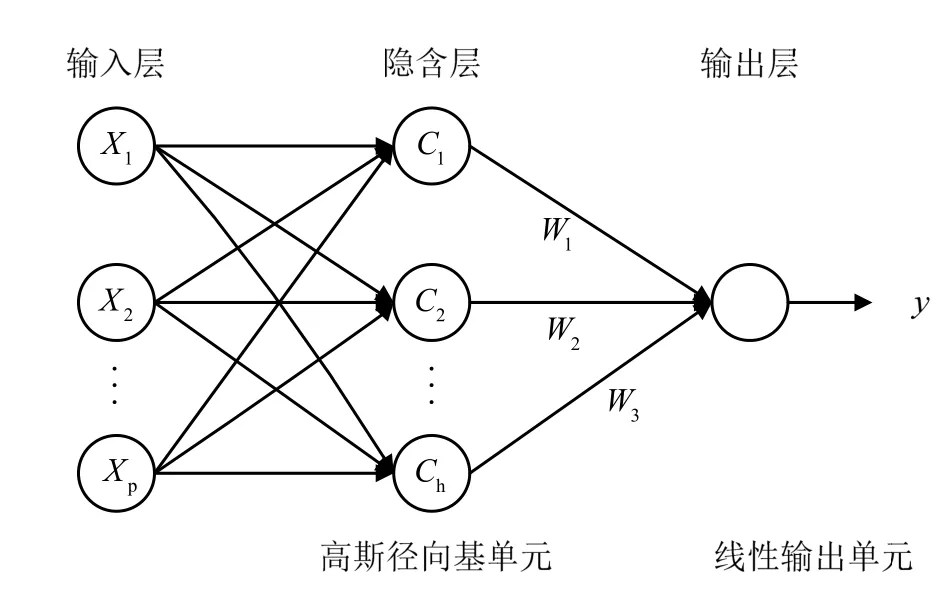
圖4 RBF 神經網絡[9] Fig.4 Radial Basis Function Neural Network[9]

RFB 神經網絡基于核函數的思想，通過隱含層將輸入向量由低維度P 映射到高維度h，從而在高緯度中實現線性可分。其網絡的權重W 可通過線性方程求解，加快了學習速度且避免了局部最小問題。RBF 神經網絡求解分為正向傳播計算誤差部分和反向傳播調整參數2 個部分。當正向傳播誤差達到所需精度或計算次數達到規定次數時完成計算。正向傳播計算公式如下：

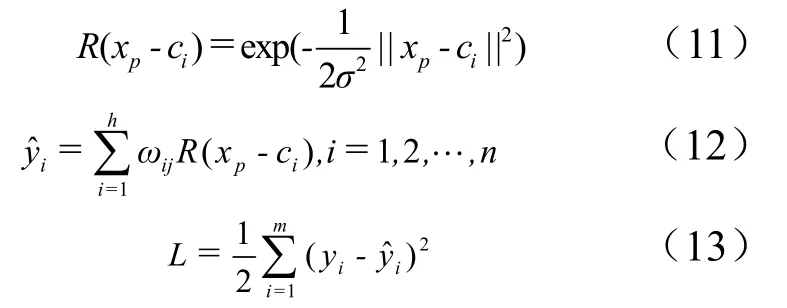
式中R ( xp-ci） 為RBF 高斯激活函數； y? 為網絡的輸出；c 為中心點；σ為中心點寬度參數；L 為損失函數。

反向傳播使用梯度下降法來進行迭代求取參數誤差，進而調整參數，詳細求解推導可參考文獻[9]，其計算公式如下：

式中α為梯度下降的學習率，學習率可根據損失函數結果和迭代次數進行調整。

2.5 替代模型效果檢驗

在完成替代模型建立后，需要對模型正確性及其效果進行檢驗。本文使用Fluent 軟件和2 種RBF 替代模型及參考文獻[10～12]中使用的KRIGING 插值模型分別求取RAE2822 翼型在Ma ∈[0.7,0.8]的阻力系數，并進行對比。對比結果如圖5 所示，可以發現2 種RBF替代模型的效果優于KRIGING 的插值效果。

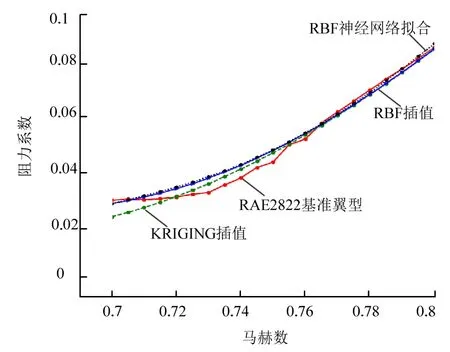
圖5 替代模型效果檢驗 Fig.5 Alternative Model Validation

2.6 遺傳算法優化求解

本文中設計因素的分布和維數以及因素彼此間的關系都未強制進行限定，因此采用馬赫數按等差數列生成，其它設計因素隨機生成來模擬遺傳算法，進行穩健翼型的優化求解。

遺傳算法[13,14]是模擬自然環境中生物種群遺傳和變異進化過程的一種自適應全局優化搜索方法，具有很好的全局尋優能力。

式（1）的優化目標可近似表示為

式中MaN 為模擬時選擇的馬赫數的個數；iMa 為規定范圍內按等差數列產生的一個馬赫數。

通過替代模型和遺傳算法結合運算，最終獲得一個穩健翼型的表面參數設計變量的值，再進行翼型參數化，即可獲得最終穩健翼型的外型。本文中的多變量遺傳算法使用二進制形式進行編碼，罰函數采用翼型的幾何約束即翼型的最大相對厚度的最小值和最大值，通過罰函數來淘汰掉不符合外形約束的翼型個體。

3 樣例及模型結果對比分析

通過對基準翼型進行穩健設計來對本文采用的RBF 替代模型方法效果進行驗證。本文以RAE2822 為基準翼型，在馬赫數Ma ∈[0.7,0.8]，雷諾數Re=6.5×106,翼型升力系數lC =0.8，翼型最大相對厚度0.1≤ d≤ 0.12的條件下，進行翼型的穩健設計，并將最終獲得的兩種RBF 穩健設計翼型性能與基準翼型和參考文獻中所采用的KRIGING 模型獲得的穩健翼型性能進行對比。

對翼型選用10 個參數變量進行表示（上下翼面各取5 個參數變量，1d ～5d 用于表示上翼面，6d ～10d 用于表示下翼面）。Hicks-Henne 中參數變量的取值范圍為：d1=[-0.006,0.006]，d2=[-0.01,0.006]，d3=[-0.006,0.008]，d4=[-0.005,0.005]，d5=[-0.005,0.01]，d6=[-0.008,0.006]，d7=[-0.001,0.01]，d8=[-0.005,0.01]，d9=[-0.005,0.005]，d10=[-0.005,0.015]。馬赫數是設計中的另一個變量，因此采用U11_165 的均勻設計表，生成165 個樣本點，每個樣本點即為一個翼型在一個馬赫數下的樣本，通過Fluent 計算出這些樣本點的阻力系數，用于RBF 替代模型建立，部分數據（未歸一化前）如表1 所示。

表1 未歸一化的部分樣本點數據 Tab.1 Unnormalized Partial Sample Point Data

在RBF 模型建立過程中需要注意的是，需要先對樣本點進行歸一化處理，以便提高模型的精度和穩健性。歸一化即將樣本點的各設計變量和目標值的取值轉化到一個統一的區間（如[0,1]）上，可通過如下min-max 方法進行歸一化：

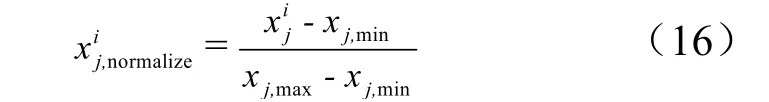
式中i=1,2,3…,n；j = 1,2…,m； xj,min為第j 個設計因素在所有樣本點中的最小值；xj,max為第j 個設計因素在所有樣本點中的最大值； xij為第j 個設計因素在第i 個樣本點上的值。

使用RBF插值和RBF神經網絡擬合進行替代模型C?d=C ?d(D,Ma)的建立。RBF 神經網絡中隱含層節點個數設置為100。在使用遺傳算法尋優時，種群中的每一個個體都代表一個翼型，取NMa=1000，即在Ma∈[ 0 .7,0.8]范圍內，按公差為0.0001 生成1000 個馬赫數，代入式（15）求得翼型對應的目標值。在遺傳算法中選擇種群規模 M=100,種群最大進化代數 K=200，交叉概率Pc=0.8，變異概率為 Pm=0.1。

最終的優化結果如表2 所示。

由表2 可知，2 種RBF 建模方法獲得的穩健翼型在Ma ∈[0.7,0.8]時，二者的阻力系數的均值與方差都小于基準翼型 RAE2822，且優于使用參考文獻中的KRIGING 模型方法獲得的同樣條件下的穩健翼型。從阻力系數的均值與方差的最終結果來看，使用RBF 神經網絡建模方法獲得的穩健翼型最佳。圖6 為2 種穩健翼型與RAE2822 翼型和KRIGING 模型獲得的穩健翼型的外形比較，可發現RBF 的2 種穩健翼型的厚度都有所減小，上表面更加平坦，且下表面后緣出現了一個非常明顯的上凹區域，表明通過RBF 替代模型獲得的兩種穩健翼型具有了明顯的超臨界翼型的特性。在圖7 翼型性能比較圖中，可明顯發現兩種穩健翼型在升力系數固定且Ma 在設定范圍條件下，其阻力系數Cd都明顯減小，均小于基準的RAE2822 翼型，優與KRIGING 模型獲得的穩健翼型。從2 種RBF 穩健翼型的最終效果來看，2 種穩健翼型都達到了本文翼型穩健設計的目標。從阻力系數的總體大小及其變化趨勢來看，通過RBF 神經網絡擬合建模方法得到的穩健翼型的效果更優。

圖6 穩健翼型外形與RAE2822 對比 Fig.6 Robust Airfoil Shapes Contrasts with RAE2822

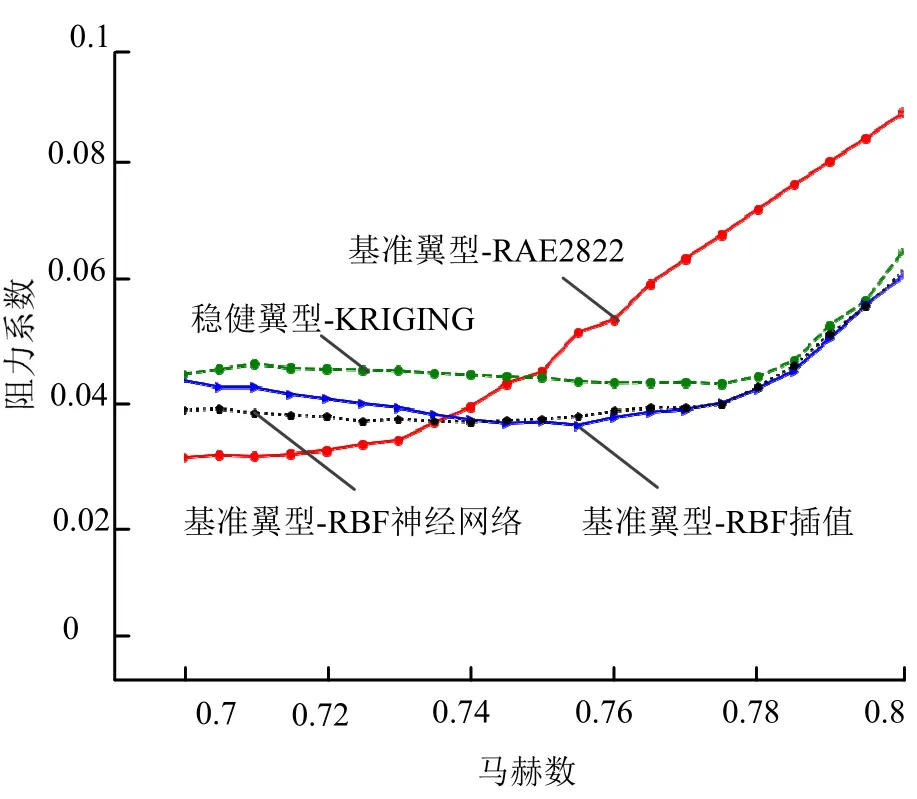
圖7 穩健翼型與RAE2822 性能對比 Fig.7 Performance Comparison between Robust Airfoils and RAE2822

4 結 論

本文使用RBF插值和RBF神經網絡擬合兩種替代模型方法來解決翼型設計中在環境發生變化時出現性能惡化的問題。本文以馬赫數的變化導致翼型阻力系數發散引起飛行器性能惡化為研究背景，通過建立RBF 的2 種替代模型，來進行穩健翼型的設計。結果表明，本文采用的2 種RBF 替代模型的方法，均達到了本文翼型穩健設計的目的，改善了在非設計狀態下干擾因素帶來的翼型性能的惡化現象。

在后續的研究中，可將RBF 替代模型方法用于三維機翼的穩健設計中。二維翼型的穩健設計結果為后續三維機翼穩健設計以及飛行器整機的穩健設計打下了一個堅實的基礎。替代模型方法在飛行器穩健設計上的應用有著重要的意義，值得進一步深入研究。