量綱分析及其在軸對稱結構動力響應中的應用

趙巨巖，王道榮，孟 剛，趙海燕，李宏杰

（1. 清華大學力學與機械工程系，北京，100084； 2. 北京航天長征飛行器研究所，北京，100076；試驗物理與計算數學國家級重點實驗室，北京，100076）

0 引 言

在工程研究的實踐中[1～3]，通常是通過1:1 的試驗來對設計結果進行驗證，但有的大型試驗在工程實現方面不僅消耗大，而且實現真實試驗條件比較困難，因此在工程實踐過程中通常用部分部段模型和縮比模型進行試驗替代，同時輔以數值仿真分析。但如何才能將模擬試驗與真實試驗的結果進行關聯，從而有效實現對真實結果的預測，成為工程實踐中亟待解決的問題，此時量綱分析[4,5]就成為解決問題的關鍵。

在應用中[6～9]量綱分析可以減少所要求解方程中的自變量，簡化理論模型。本文針對具有雙層結構材料的軸對稱柱形殼體，運用量綱分析方法，依據模型和原型基本相似的特點，開展在脈沖載荷作用下的動力學響應分析，在特定條件下建立無量綱因變量與自變量之間的函數關系，通過3 個不同幾何尺寸的縮比模型件對相關結論進行驗證，為研究大尺寸復雜結構 體脈沖載荷作用下動力學響應提供一種重要的方法。

1 物理模型

研究對象為一個雙層圓柱形殼體，兩層結構層由材料1 和材料2 組成，兩種材料都為各向同性、理想塑性材料，滿足Mises 屈服準則。材料1 的密度為1ρ ，楊氏模量為1E ，泊松比為1ν ，屈服應力為1Y ，厚度為H1；材料2 的密度為2ρ ，楊氏模量為2E ，泊松比為2ν ，屈服應力為2Y ，厚度為H2。圓柱形殼體長度為L、外半徑為R，如圖1 所示。殼體的任何響應都與自身的材料特性、結構特性、載荷的分布特征以及作用時間緊密相連，本模型只以余弦加載為研究對象，余弦加載的特點為殼體在180°范圍內其外側受到沿延徑向的壓力在軸向是均勻分布的、而沿軸向θ 按半余弦分布，載荷為 ( )cosθp t，如圖2 所示。同時假設載荷在各點隨時間的變化規律是以如下特征而在各點同步加載的：其在極角 θ =0°處的壓力峰值為 p0、作用總時間為τ0、加卸載規律為等腰三角形，如圖3 所示，其數學形式如式（1）所示。

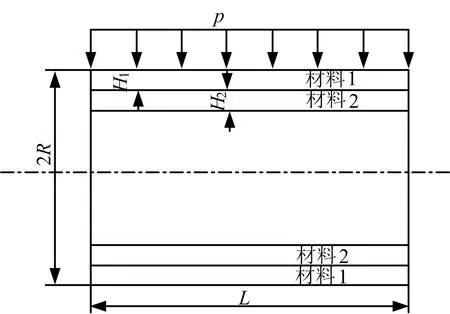
圖1 圓柱形殼上側軸向受均布載荷p 示意 Fig.1 Schematic Diagram of Iaxal Uniform Load p on the Upper Side of a Cylindrical Shell

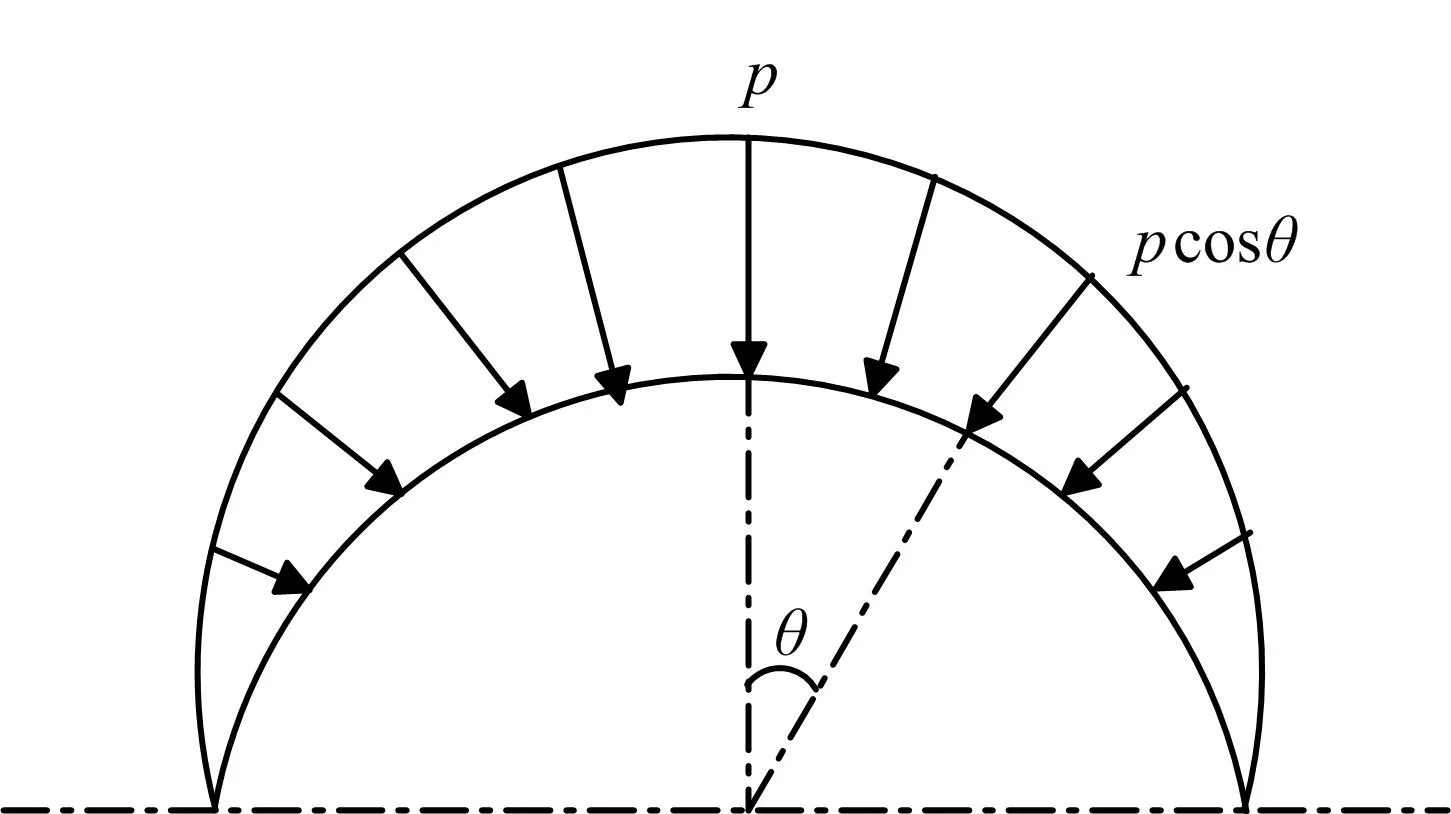
圖2 圓柱形殼上側徑向受余弦載荷p 示意 Fig.2 Schematic Diagram of Lateral Side of Cylindrical Shell Subjected to Cosine Load p

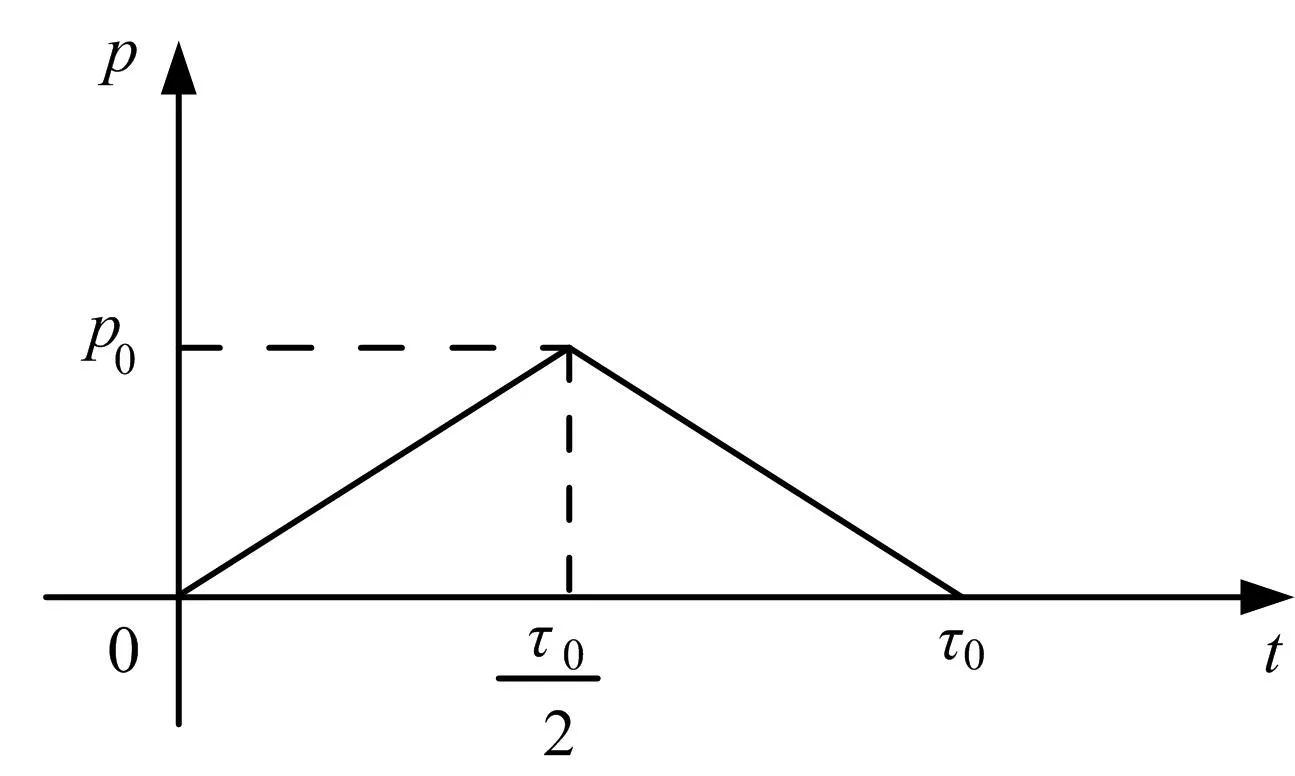
圖3 三角形壓力脈沖載荷 Fig.3 Triangular Pressure Pulse Load

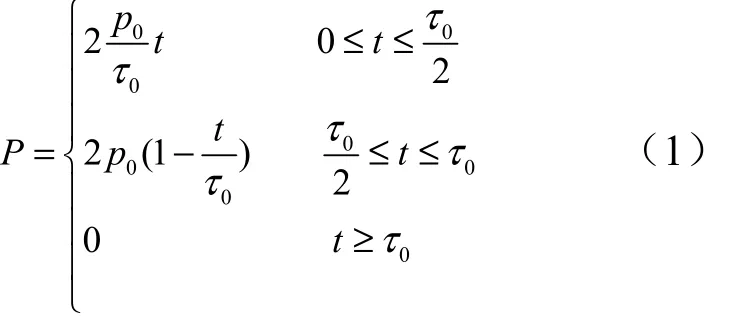
對于此種分布規律和時程特點的脈沖載荷，圓柱形殼上的動力學響應只依賴于2 個參數：0p 和0τ 。這里只以研究殼體受載區域的中心點最大等效應力maxσ和最大等效應變maxε 隨外載的變化規律為例。

2 問題求解之量綱分析

針對上述物理模型，可以確定問題的主自變量為：殼體長度 L、外徑R、厚度 H1和 H2、材料物性參數ρ1,E1,ν1,Y1和 ρ2, E2,ν2,Y2、脈沖載荷參數 p0和τ0，圓柱形殼體中最大等效應變 εmax、最大等效應力 σmax是這些自變量的函數，即：

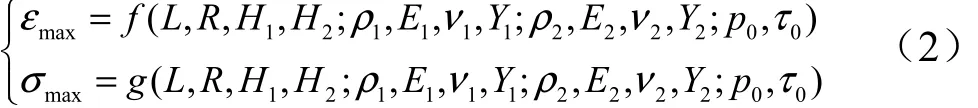
式中f(x)，g(x)為函數關系；用L，M，T（長度、質量、時間）單位制進行分析， 應變 εmax為因變量，無量綱； L，R，H1，H2的量綱均為長度L； ρ1， ρ2為質量密度，量綱為ML?3；因變量 σmax和自變量 E1，E2，Y1，Y2和 p0為應力，量綱為ML?1T?2；ν1，ν2為自變量，無量綱； τ0為自變量，量綱為T 。

式（1）和式（2）中有14 個自變量，3 個獨立的量綱，取其中任何3 個量綱彼此獨立的物理量為基本量。例如，取基本量為：圓柱形殼體半徑R、材料1的密度1ρ 和楊氏模量1E 。以上述3 個量為基本量組變換其它自變量和因變量的無量綱表達式，如下所示：

因變量為

自變量為

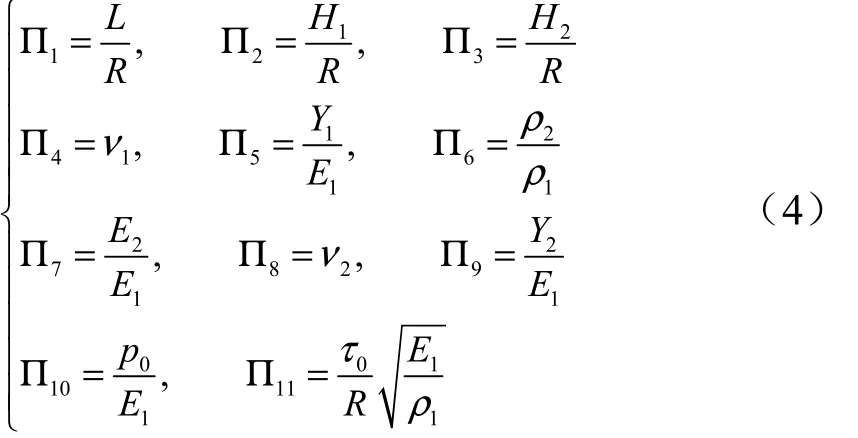
根據Π 定理，把有量綱量的函數關系式（2）寫成無量綱函數，最大等效應變maxε 和無量綱最大等效應力表達式，如下式：

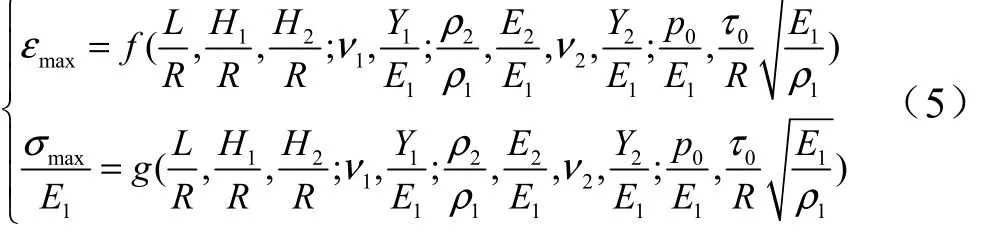
式（5）中，對無量綱因變量起作用的自變量共11 個，可分為4 類：第1 類是幾何相似準數，反映的是對結構幾何尺度相似要求；第2 類是材料相似準數，反映的是對結構材料相似要求；第3 類是加載的載荷動力學相似準數，反映的是對加載載荷強度的動力相似要求；第4 類是以在材料中縱波波速傳過結構特征尺寸所需的時間為基準，度量加載載荷的歷時。

3 對問題相似律的進一步分析

為了簡單起見，假設圓柱形殼體長度L 為無限大，三維響應問題可視為二維平面問題，殼體長度L 將不影響柱殼體中的等效應變和等效應力，無量綱自變量減少為10 個。

用模型試驗來確定無量綱函數f 的具體形式必須保證模型和原型的物理相似，也就是要求模型和原型的歸一化最大等效應變maxε 與最大等效應力分別相等。當模型中所有相關參數的無量綱量與原型中對應的無量綱量都相等時，通過模型試驗所測得的歸一化最大等效應力和最大等效應變值就與原型里的和相等（注：下標m 為模型，p為原型）。

根據實際作用的力學環境，對上述問題進行進一步的簡化。

a）模型與原型滿足幾何相似條件，即：

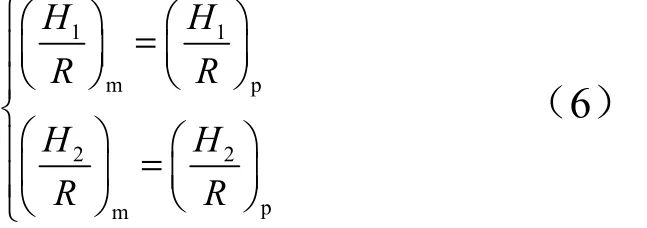
b）模型和原型選用相同的材料，保證材料相似條件，即：

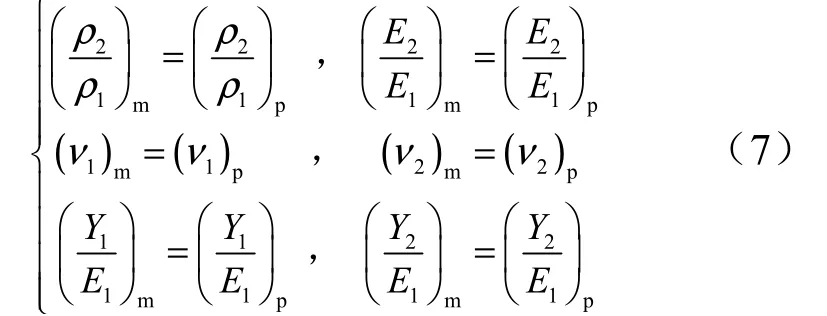
也就是材料相似準數為常數，然后就只剩下加載載荷的動力相似準數：

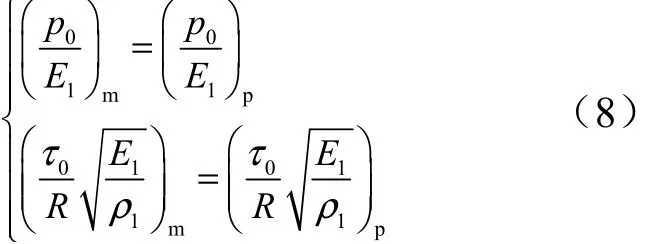
式（5）可簡化為

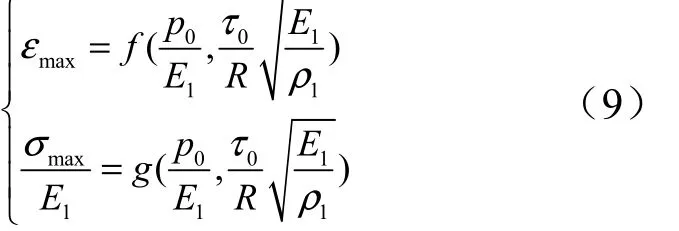
如果模型和原型完全物理相似，則：

除式（10）外，還應有表示加載持續時間相似的動力學相似條件：

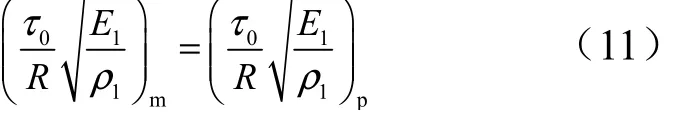
由相似條件可以得出如下結論：假設原型和模型的幾何縮比為

則式（11）可寫為

這就是說，在滿足模型和原型其它相似準數都相等的條件下，當結構的幾何尺度縮小n 倍的同時加載載荷的時間也縮小n 倍時，結構的動力響應的無量綱量是完全相等的，即：

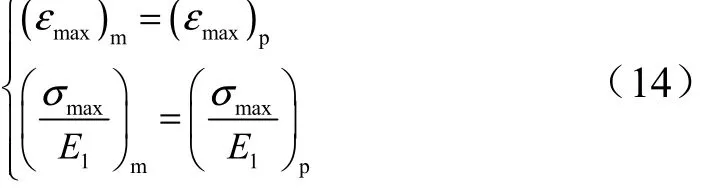
此外，如果不把加載載荷參數0p 和0τ 看做兩個獨立的量，而只是關心它們的乘積000τ=I p ,考慮式（12），則式（13）將進一步變換成如下沖量載荷形式，即：

由式（15）可知，在模型和原型材料和幾何尺寸完全相似的情況下，要使兩者動力學響應形同，幾何尺寸縮比為n 時，加載的沖量也要縮比為n 倍。

4 相似準則的試驗驗證

4.1 試驗設計

為驗證式（15）的科學性，設計了大小成幾何縮比的3 個圓柱殼體，縮比模型試驗件材料為LY12 鋁合金，幾何尺寸比為1:1.5:2，3 個圓柱形縮比模型樣件幾何尺寸（厚度/直徑/高）分別為：2.0 mm/170 mm/200 mm/、3.0 mm/255 mm/300 mm、 4.0 mm/340 mm/400 mm，如圖4 所示。

圖4 3 個圓筒試驗件圖示意 Fig.4 Diagram of Three Cylindrical Test Pieces

為研究在動態加載下圓柱殼體的動力響應，對3 個圓筒施加如圖2 的余弦載荷，本次試驗布置1～5的5 個測點，分別對應加載強度峰值0°、45°、-45°、90°和135°的位置，測量應變為環向應變。在加載設計中，比沖量載荷大小按照小圓柱殼體、中圓柱殼體和大圓柱殼體順序，即：1:1.5:2。如果滿足相似律，那么當加載載荷呈幾何縮比時3 個圓筒對應測點的應變值大小應該相等。

4.2 試驗結果及分析

表1 為3 個不同圓筒殼體5 個測點環向最大拉伸應變情況分析。

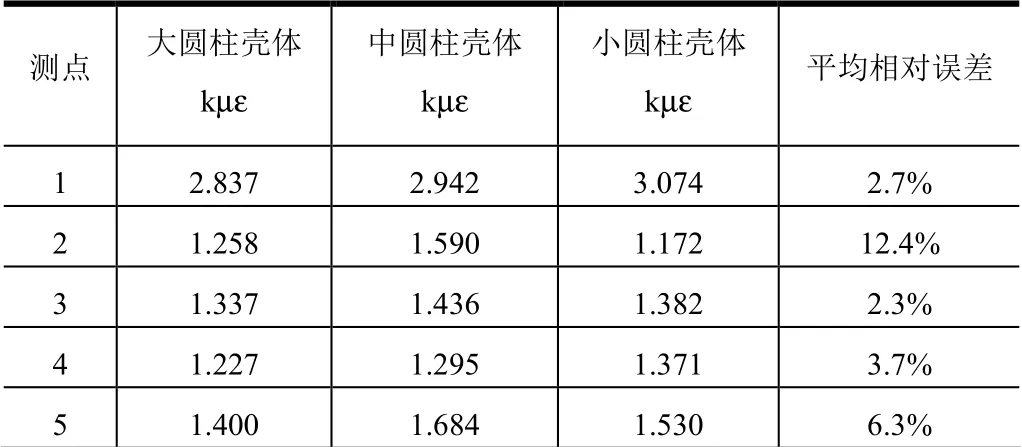
表1 不同殼體試驗最大拉伸應變數據分析 Tab.1 Analysis of Maximum Tensile Strain Data of Different Shell Tests

對測點1 來說，大圓柱殼體、中圓柱殼體和小圓柱殼體按照比沖量縮比規律加載，拉伸應變分別為2.837 kμε、2.942 kμε和3.074 kμε，平均應變為2.951 kμε，相對于平均應變的相對誤差分別為3.8%、0.3%和4.1%，平均相對誤差為2.7%。在誤差許可范圍內認為測點1 在3 次試驗中的最大拉應變值相等，驗證了量綱分析的相似律結論。同樣的結論可以用到對測點2～5 的測量結果分析中。由表1 可知，除測點2在中圓柱殼體試驗中平均相對誤差達到12.4%，其余各個點在試驗中相對誤差對小于10%，并且大部分的相對誤差在5%附近。由于測點分布區域較廣，因此本次試驗較好地驗證了圓柱殼體在滿足幾何和材料相似情況下，動態加載下結構響應具有相似性的特點。

5 結 論

從工程實際問題需求出發，以量綱理論為指導，通過建立在特定條件下無量綱因變量與無量綱自變量間的函數關系，經過函數依賴關系的分析研究，結論如下：

a）在模型和原型材料和幾何尺寸完全相似的情況下，當殼體結構只含有2 個獨立參數時，結構的無量綱因變量只與2個加載載荷參數的無量綱自變量有關。

b）在模型和原型幾何相似、所取材料相同的條件下，當原型到模型的幾何縮比為n 倍時，在原型材料和模型材料幾何尺寸完全相似的情況下，要使原型和模型動力學響應相同，當幾何尺寸縮比為n 倍時，外載荷加載的沖量也要縮比n 倍。

c）開展3 個不同幾何尺寸縮比試件動態余弦加載試驗，通過5 個測量點應變測量數據的分析，結果證明理論推導是正確的。