柔性太陽翼疊層電池彎曲適應性仿真與設計

許京荊 韋祎 陳萌炯 馬聚沙

摘要：航天器在軌進、出地影時，基于復合結構柔性基板的柔性太陽翼疊層電池在高、低溫交變作用下會產生熱彎曲變形。針對這一問題，采用有限元建模仿真，分析由太陽電池、蓋片膠和抗輻照玻璃蓋片組成的疊層電池的彎曲適應性，計算不同結構尺寸、不同疊層材料參數的疊層電池在跨中彎曲載荷下的最大應力。借助響應面技術研究設計變量與復合結構性能之間的關系，采用目標驅動優化分析，獲得理想的結構尺寸參數。結果表明：疊層電池的宏觀力學性能取決于微觀不同疊層材料的組合方式;等效彈性模量不是定值，而是與疊層材料的參數有關;彎曲工況的失效模式取決于電池單體的最大拉應力，而不是宏觀表征的整體彎曲強度。

關鍵詞：柔性太陽翼; 疊層電池; 彎曲; 應力; 有限元

中圖分類號：V214.11; TB115.1

文獻標志碼：B

Bending adaptability simulation and design of

solar cell integrated cover of flexible solar array

XU Jingjing， WEI Yi， CHEN Mengjiong， MA Jusha

（College of Mechanical Engineering and Automation， Shanghai University， Shanghai 200072， China）

Abstract：

During the illumination-shadow period of orbit， the cell integrated cover based on the composite flexible substrates of the flexible solar array produces bending thermal deformation under alternating high and low temperature. As to this problem， the flexural adaptability of cell integrated cover consisting of solar cell， adhesive cover and irradiation resistant glass cover， is analyzed using finite element modeling and simulation. The maximum stresses of the cell integrated cover with different structural sizes and different laminated material parameters under mid-span bending loads are calculated. The relationships between design variables and performance of composite structures are studied by response surface methodology. The dimension parameters of the structure are obtained using target-driven optimization analysis. The results show that the macro-mechanical properties of the cell integrated cover depend on the combination of different micro-stacked materials; the equivalent elasticity modulus is not a fixed value， but it is related to the parameters of laminated materials; the failure modes under bending conditions depend on the maximum tensile stress of the cell monomer rather than the overall bending strength as macroscopically characterized.

Key words：

flexible solar array; cell integrated cover; bending; stress; finite element

收稿日期：2019-06-19

修回日期：2019-07-01

作者簡介：

許京荊（1970—），女，浙江東陽人，博士，副教授，研究方向為有限元數值分析，（E-mail）xjj125@shu.edu.cn

0?引?言

柔性太陽翼質量功率比高、收攏體積小，在航天器發射體積或質量受限的特殊應用領域中的地位不可替代，例如大面積空間電站、空間站軌道艙、超高功率大型衛星等均適合配備柔性太陽翼。[1-2]我國在研和國外主流的低地球軌道（low earth orbit， LEO）柔性太陽翼電池均采用柔性基板粘貼剛性疊層（光照面粘貼抗輻照玻璃蓋片）的結構形式[3]，其在軌進、出地影時，復合結構柔性基板在高、低溫交變作用下會產生以彎曲形式為主的熱變形[4]。

據相關報道，哈勃望遠鏡卷壓型柔性太陽翼在1990年發射入軌后的工作校驗期間出現過太陽翼彎曲撓度過大、太陽翼局部供電損失的故障[5]，后經地面試驗與仿真分析，確定故障是由柔性太陽翼低剛度非對稱幾何結構的熱失配造成基板彎曲過載所致的，太陽翼局部供電損失是由于疊層電池受基板變形影響發生非預期的碎裂而引起部分供電子電路開路所致的。類似的疊層電池碎裂導致太陽翼供電失效的案例，美國地球資源衛星Landsat-2和Landsat-?4也曾先后出現過。[6]

柔性太陽翼在軌彎曲過載引起廣泛關注后，研究人員開始在設計階段尋求一種快速高效的設計方法，對太陽翼溫度、熱變形和各部分的彎曲適應性進行直觀分析。隨著計算機的發展，CAE有限元仿真分析以計算精度高、復雜形狀適應性強、分析效率高等優點被廣泛采用。ZIMBELMAN等[7]仿真研究LEO空間環境下太陽翼在收攏-展開工況下的溫度場分布;THOMTON等[8]仿真分析宏觀溫度梯度及其變化，研究太陽翼溫度變化引起彎曲變形導致熱顫的機理;丁延衛等[9]和張燕娜等[10]從基板設計角度出發，對太陽翼基板的熱變形開展適應性分析與結構優化設計。

本文從疊層電池設計出發，以LEO柔性太陽陣用疊層電池為研究對象，采用有限元建模仿真結合力學試驗的方法，開展疊層電池抗彎曲性能分析和結構設計優化，獲取疊層電池的等效材料參數、建立有限元分析模型，并得到優化的疊層電池結構尺寸參數。

1?疊層電池力學性能參數確定

疊層電池由鍺襯底太陽電池封裝抗輻照摻鈰石英玻璃構成，其復合結構主要包括鍺襯底3J-GaAs太陽電池（電池單體中鍺襯底厚度占比為85%）、硅膠和摻鈰石英玻璃。[11]

鍺為立方晶系的單晶體材料。用正交各向異性材料的主軸坐標系表示應力分量和應變分量，彈性應力-應變關系由廣義胡克定律確定，即εm=

Cm

σm。在單晶材料的3個主軸方向上，材料的彈性特性相同，應力-應變關系矩陣為

Cm=

1E-νE-νE000

-νE1E-νE000

-νE-νE1E0000001G0000001G0000001G

（1）

式中：E為材料主軸方向的彈性模量，MPa;ν為泊松比;G為剪切模量，MPa。單晶立方晶系各向異性材料通常給出[100]、[110]和[111]方向的彈性模量E100?，E110?和E111?（疊層電池彎曲特性測試和分析時需結合實際情況確定具體參數，太陽電池鍺片劃片方向不同時材料彈性模量取值不同）。確定彈性模量和泊松比后可得到剪切模量G，

1G=4Ex-2-2νE

（2）

式中：Ex表示彈性模量E100?、E110?和E111?，MPa。

采用DMA Q800動態熱機械分析儀開展太陽電池鍺襯底三點彎曲彈性模量測定試驗。鍺片試樣件規格為30.0 mm×5.0 mm×0.20 mm，試樣制備按太陽電池劃片方向分為水平方向[1?10]、垂直方向[110]、+45°方向[100]和-45°方向[010]。根據應力-應變數據擬合，得到水平方向的彈性模量平均值為E1?10?=1.33×105 MPa，垂直方向的彈性模量平均值為E110?=1.38×105 MPa，水平與垂直方向的彈性模量相差不大，均值為1.35×105 MPa;與水平方向夾角45°方向的彈性模量平均值為E100?=1.05×105 MPa。實測的水平與垂直方向都與材料主方向成45°，而45°測試方向為材料主軸方向，計算得到剪切模量G=6.36×104 MPa。

抗輻照摻鈰石英玻璃為脆性材料，各向同性材質，試樣規格為30.0 mm×10.0 mm×0.125 mm，試樣制備后進行4組三點彎曲試驗。根據應力-應變數據擬合，得到彈性模量均值為8.25×104 MPa。

2?疊層電池有限元建模

采用ANSYS建立仿真模型，按照初步設計結果設置模型尺寸。疊層電池總尺寸為20.0 mm×10.0 mm×0.29 mm，其中：太陽電池單體為鍺，厚度為0.15 mm;中?間為硅膠，厚度為0.02 mm;頂部為石英玻璃，厚度為0.12 mm。疊層電池的幾何模型見圖1。

電池單體主軸取45°方向，材料本構關系采用正交各向異性彈性模型，彈性模量E100?=1.05×105MPa（三點彎曲測試均值），泊松比ν=0.27，計算剪切模量G=6.36×104 MPa;玻璃和硅膠為各向同性彈性模型。疊層電池材料力學參數見表1。

模型采用三維實體-殼單元，單元大小為0.14 mm，對疊層電池幾何模型進行網格劃分，見圖2。網格劃分后節點總數為42 340個，單元總數為31 104個。

3?模型適用性分析

借助試件彎曲試驗，比對仿真結果，開展模型適用性分析。

疊層電池三點彎曲試驗載荷示意見圖3，試驗照片見圖4，應力-應變測試結果見圖5。試樣跨距為20.0 mm，寬度為10.0 mm，總厚度為0.29mm，最大負荷F=0.877 N，對應跨中最大撓度t=0.26 mm，宏觀抗彎強度為31.4 MPa，彈性模量為2.86×104 MPa。

參考實際試驗加載的邊界條件，對疊層電池模型進行有限元仿真。根據最大撓度，在z方向施加0.26 mm位移，兩端簡支，允許繞y軸轉動。對比最終仿真結果與試驗結果，分析模型的適用性。疊層電池位移加載和最終輸出結果見圖6～15。

仿真結果顯示：疊層電池整體最大變形為0.256 mm;?疊層電池跨中平均撓度為0.256 mm;計算獲得的疊層電池反作用力為0.896 N，試驗值為0.877 N，二者誤差為2.17%;疊層電池總體等效應力為77.98 MPa;太陽電池單體最大拉應力為80.38 MPa;?玻璃最大主應力為45.91 MPa;硅膠等效應力為0.08 MPa;?疊層電池跨中截平面最大主應

力平均值為29.06 MPa。在疊層電池中心位置沿厚度方向設置一條路徑，并給出疊層電池跨中中心路徑上的線性化正應力，電池單體側拉應力最大值為32.70 MPa，玻璃側壓應力最大值為-32.70 MPa，與試驗彎曲強度31.40 MPa接近。隨著試件厚度由0增大到0.29 mm，太陽電池單體的應力從最大拉應力80.38 MPa線性變化到最大壓應力-75.3 MPa，硅膠的應力很小。

由小樣試件彎曲試驗結果與仿真結果的對比可知：小樣實測最大負荷為0.877 N，與仿真最大負荷0.896 N的誤差為2.17%;小樣實測宏觀抗彎強度為31.40 MPa，與仿真電池單體/玻璃抗彎強度32.70 MPa?的誤差為4.14%。因此，模型仿真結果與實測結果接近，可用于疊層電池結構優化設計。

4?疊層電池結構設計優化

在獲得疊層電池復合結構材料主要力學參數與仿真模型后，開展疊層電池結構優化設計，主要考慮太陽電池長度、寬度和厚度，尺寸規格參數選取見表2。按表2設計規格建立有限元數值模型，對疊層電池進行仿真分析。

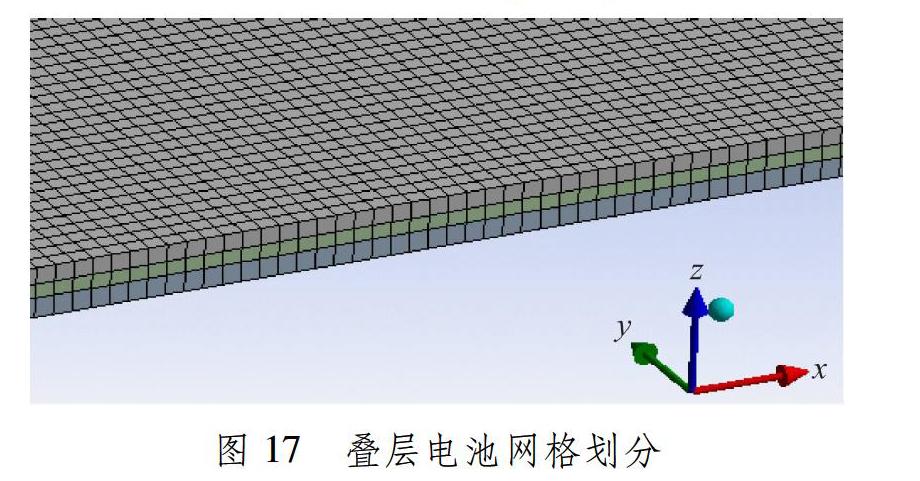
各規格試件幾何模型和網格劃分方法同前文。規格1電池板尺寸為40.0 mm×30.0 mm×0.36 mm;3層材料中太陽電池單體厚度為0.14 mm，中間硅膠厚度為0.10 mm，頂部石英玻璃厚度為0.12 mm，其三維幾何模型見圖16。其他規格試件網格劃分均相似。在數值模擬過程中，電池單體取主軸方向為0°，材料本構關系采用正交各向異性彈性模型，主軸彈性模量取E100?=1.05×105 MPa（三點彎曲測試平均值），泊松比ν=0.27，計算剪切模量G=6.36?×104 MPa。玻璃和硅膠為各向同性彈性模型，彈性模量和泊松比的數據取自表1。采用三維實體-殼單元，單元大小為0.12 mm，對疊層電池幾何模型進行網格劃分，見圖17，網格劃分節點總數為336 340個，單元總數為250 500個。

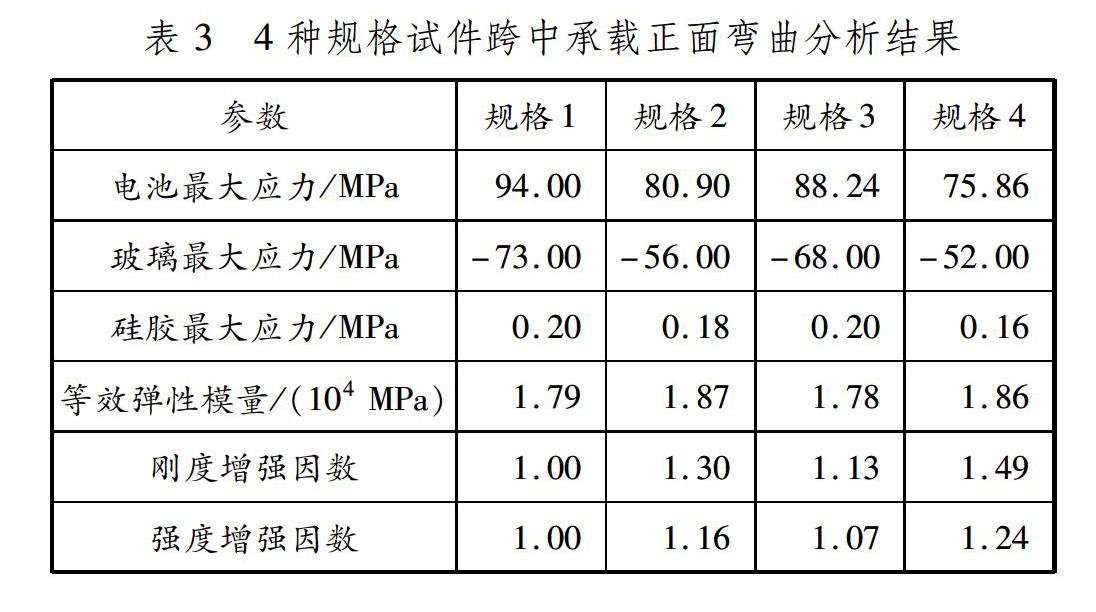
根據太陽翼設計技術要求，設置疊層電池跨中承載力為2.396 7 N，對4種規格試件的正面（玻璃面）彎曲進行分析，結果匯總見表3。

分析結果顯示，在4種規格的試件中，規格38.3 mm?×31.3 mm×0.39 mm的試件許用承載力最大。疊層電池的宏觀力學性能取決于微觀不同疊層材料的組合方式，等效彈性模量與疊層材料的參數有關，不是定值。彎曲工況下疊層材料失效取決于最薄弱環節，即某電池單體處，其彎曲失效取決于電池單體的最大拉應力，而不是宏觀表征的整體彎曲強度。這一點可由規格38.3 mm×31.3 mm×0.39mm試件的強度和剛度要大于規格40.0 mm×30.0 mm×0.39 mm試件的強度和剛度證實：在同等載荷的情況下，后者最大彎曲應力應該更小，而實際卻相反。所以，用整體彎曲強度作為結構失效的評判準則是不合適的。

另外，對4種規格的疊層電池跨中承載進行正、反面（太陽電池面）彎曲分析，得到如下結果。

（1）疊層電池的失效取決于疊層結構和加載方式，實質是由于電池單體或玻璃材料的失效引起的。由于厚度不同，電池單體和玻璃失效的可能性都存在，如規格40.0 mm×30.0 mm×0.34 mm試件玻璃面加載與規格40.0 mm×30.0 mm×0.39 mm試件太陽電池面加載都是電池單體先達到許用拉應力，而規格40.0 mm×30.0 mm×0.34 mm試件太陽電池面加載是玻璃先達到許用拉應力。

（2）當僅考慮拉伸失效時，太陽電池面加載的許用承載力高于玻璃面加載的許用承載力。

（3）依據疊層電池的宏觀性能評定其失效行為或者其強度和剛度行為不合適。同樣電池規格，正、反面加載得到的彈性模量和彎曲強度不同：受硅膠層厚度的影響，規格40.0 mm×30.0 mm×0.34 mm試件玻璃面加載的彈性模量為2.06×104 MPa，太陽電池面加載的彈性模量為1.92×104 MPa，相差1.07倍;?規格40.0 mm×30.0 mm×0.39 mm試件玻璃面加載的彈性模量為1.87×104 MPa，太陽電池面加載的彈性模量為1.66×104 MPa，相差1.13倍。

（4）可以根據仿真數據推算疊層電池的抗彎強度，如規格40.0 mm×30.0 mm×0.34 mm試件，玻璃面加載的抗彎強度為41.0 MPa×3=123.0 MPa，太陽電池面加載的抗彎強度為46.5 MPa×3=139.5 MPa;規?格40.0 mm×30.0 mm×0.39 mm試件，玻璃面加載的抗彎強度為28.6 MPa×3=85.8 MPa，太陽電池面加載的抗彎強度為44.0 MPa×3=132.0 MPa。

為獲得疊層電池具體尺寸更詳盡的相關力學性能特征，基于前面給定規格的疊層電池結構布局，以各層厚度、長度和寬度為設計變量，以滿足跨中彎曲強度設計要求為目標，建立參數化模型，通過試驗設計技術和響應面法研究設計變量與疊層電池結構性能之間的關系，采用目標驅動優化分析（ANSYS中的Workbench GDO模塊）獲得最佳的疊層電池抗彎結構，強度和尺寸約束范圍見表4。考慮跨中彎曲的結構優化，強度約束條件根據許用應力設置。

確定初始計算的疊層電池結構參數，將疊層電池的長度、寬度和各層厚度作為設計變量，指定電池單體最大拉應力、玻璃最大主應力、膠層等效應力和等效彈性模量為輸出變量，采用試驗設計方法確定45組樣本進行仿真計算，基于響應面技術得到設計變量與疊層電池的結構性能之間的關系和最佳的疊層電池抗彎結構。采用目標驅動算法計算，優化分析結果設置長度為40.0 mm，寬度為30.0 mm，總厚度為0.36 mm，各層需要滿足強度指標。篩選優化方案，確定疊層電池長度為38.6 mm，寬度為32.3 mm，長寬比為1.2，單體電池厚度為0.23 mm，玻璃厚度為0.06 mm，硅膠厚度為0.02 mm，總厚度為0.31mm，電池單體最大拉應力為91 MPa，承載力為4.6 N，單位寬度承載力為0.144 N/mm，總變形為0.986 mm。

5?結束語

由LEO柔性太陽陣用疊層太陽電池抗彎曲設計和有限元建模仿真分析可知，通過引入計算機輔助有限元仿真，可高效分析疊層太陽電池不同現行尺寸結構的力學性能，改進薄弱環節、優化設計。本文建立一種LEO柔性太陽翼疊層電池有限元分析模型，并得到在設計限定條件下疊層電池抗彎性能優化后的具體結構尺寸參數，為柔性太陽翼疊層電池設計提供參考。

參考文獻：

[1]

聞新， 紀龍， 朱詩嘉. 航天器太陽電池陣列的發展歷程[J]. 中國航天， 2011（12）： 23-27.

[2]JONES P A，SPENCE B R. Spacecraft solar array technology trend[J]. IEEE Aerospace and Electronic Systems Magazine， 2011， 26（8）： 17-28.DOI： 10.1109/MAES.2011.5980605.

[3]于輝， 孫彥錚， 金海雯. 空間站柔性太陽翼電池電路部分設計初探[J]. 電源技術， 2013， 37（3）： 395-397. DOI： 10.3969/j.issn.1002-087X.2013.03.017.

[4]趙志萍， 趙陽東. 大面積太陽翼國外發展研究[J]. 沈陽航空航天大學學報， 2014， 31（3）： 39-?44. DOI： 10.3969/j.issn.2095-1248.2014.03.008.

[5]MUROZONO M，THORNTON E A. Buckling and quasistatic thermal-structural response of asymmetric rolled-up solar array[J]. Journal of Spacecraft and Rockets， 1998， 35（2）： 147-155. DOI： 10.2514/2.3322.

[6]馮偉泉. 歸因于空間環境的航天器故障與異常[J]. 航天器環境工程， 2011， 28（4）： 375-389.

[7]ZIMBELMAN D F，WELCH R V， BORN G H. Optimal temperature estimation for modeling thermal elastic shock disturbance torque[J]. Journal of Spacecraft and Rockets， 1991， 28（4）： 448-?456. DOI： 10.2514/3.26265.

[8]THOMTON E A，KIM Y A. Thermal induced bending vibration of a flexible rolled-up solar array[J]. Journal of Spacecraft and Rockets， 1993， 30（4）： 438-?448. DOI： 10.2514/3.25550.

[9]丁延衛， 王曉耕， 張立華， 等. 碳纖維/鋁蜂窩太陽翼基板熱變形分析[J]. 航天器工程， 2009， 18（4）： 44-?48. DOI： 10.3969/j.issn.1673-8748.2009.04.008.

[10]張燕娜， 趙泓濱. 太陽電池陣基板結構優化設計[J]. 空間電子技術， 2018， 15（2）： 49-53. DOI： 10.3969/j.issn.1674-7135.2018.02.008.

[11]馬世俊. 衛星電源技術[M]. 北京： 中國宇航出版社， 2001： 142-184.