基于邊劃分理論的謠言傳播模型

羅靖宇 唐寧九

摘 要：針對謠言傳播過程中傳播態節點恢復時會受其鄰居節點狀態影響的問題，提出了一種基于邊劃分理論的謠言傳播模型。首先，使用改進的邊劃分理論建立起謠言傳播的動力學方程組，推演出謠言在復雜網絡上的傳播范圍值和爆發閾值;然后，通過數值仿真實驗研究網絡結構、傳播概率和基礎恢復概率等參數對謠言傳播的影響;在此基礎之上，提出了可以有效控制謠言傳播范圍和爆發閾值的免疫策略。理論分析和仿真結果表明，與經典的SIR模型相比，提出的謠言傳播模型縮短了謠言傳播的周期，傳播態節點比例的峰值則有小幅提高。對比實驗發現，與現有的隨機免疫策略相比，當謠言的傳播概率較大時，優先免疫連接小度節點的邊能得到更小的謠言傳播范圍;反之，當謠言的傳播概率較小時，優先免疫連接大度節點的邊可以有更小的謠言傳播范圍。研究結果表明，提出的謠言傳播模型符合謠言消退期的特征，為謠言傳播的預測與控制提供了理論和數值上的支持。

關鍵詞：復雜網絡;易感態感染態恢復態模型;謠言傳播;邊劃分理論;免疫策略

中圖分類號：TP393

文獻標志碼：A

Rumor propagation model based on edgebased compartmental theory

LUO Jingyu， TANG Ningjiu*

College of Computer Science， Sichuan University， Chengdu Sichuan 610065， China

Abstract：

Aiming at the problem that spreader nodes will be influenced by their neighbors during the recovery in the rumor propagation process， a rumor propagation model based on edgebased compartmental theory was proposed. Firstly， a set of dynamic equations were established using the improved edgebased compartmental theory， and the propagation range and breaking threshold were theoretically analyzed. Then the influence of factors including network structure， propagation probability and basic recovery probability were analyzed through numerical simulation. Finally， an effective immunization strategy to control rumor propagation range and breaking threshold was presented on the above basis. The results of theoretical analysis and numerical simulation show that， compared with the classical SIR （SusceptibleInfectedRecovered） rumor propagation model， the presented model decrease the period of rumor propagation and increase the peak of the propagation of spreader nodes slightly. Through comparison experiments with the random immunization strategy， in the proposed strategy the edges with higher product of the degrees of two nodes were immuned preferentially to obtain better effect when rumor has minor propagation probability， and the edges with lower product of the degrees of two nodes were immuned preferentially to obtain better effect when rumor has larger propagation probability. Study results indicate that the presented model conform to the characteristics of rumor fading away phase and can provide theoretical and numerical support for rumor prediction and control.

Key words：

complex network; SusceptibleInfectedRecovered （SIR） model; rumor propagation; edgebased compartmental theory; immunization strategy

0?引言

隨著人類日常生活的網絡化，微博、Twitter等在線社交網絡開始興起。由于這類在線社交網絡具備用戶門檻低、消息傳播速度快、地域限制小等特點，在這些平臺上的信息傳播的速度和范圍均遠遠超過傳統傳播方式。但這種現象在給人們的日常生活帶來便利的同時，也會帶來謠言大規模傳播且難以控制的負面影響，因此，需要研究社交網絡上謠言傳播的規律并在此基礎上得到適當的謠言傳播控制策略。社交網絡上謠言等信息的傳播都屬于社會傳播的范疇，可以被描述成“復雜網絡上的傳播動力學”。

復雜網絡是近年來新興的一門學科，人類生活中的眾多現象例如新科技的傳播[1]和謠言傳播等都可以被納入復雜網絡的研究范圍。1998年康奈爾大學的Watts博士和Strogatz教授提出的具有小世界特性的WS網絡[2]以及1999年Barabási和Albert提出的具有無標度特性的BA網絡[3]標志著復雜網絡的誕生。在此之后，相關研究人員不斷地運用復雜網絡來解決各個領域中的問題，在輿情、謠言等社會行為的傳播研究領域，研究人員廣泛采用的傳播動力學模型是易感態感染態恢復態（SusceptibleInfectedRecovered， SIR）模型[4]。在SIR模型中，參與傳播的每個節點在任意時刻只能處于三種狀態中的一種：易感態（Susceptible）、感染態（Infected）和恢復態（Recovered）。節點處于易感態就表示該節點尚未參與到信息的傳播過程中，在傳播開始之后的每一個時間步，處于感染態的節點會以傳播概率λ向鄰居節點中的易感態節點傳播信息，并且會以概率γ進入到恢復態，恢復態節點將不會再參與到信息的傳播過程中。盡管SIR模型作為一種經典的非可逆傳播模型可以很好地描述出真實中謠言傳播的特性，但依然有很多影響謠言傳播的屬性沒有被考慮到。國內外研究者分別從社會網絡結構[5]、社會傳播的加強效應[6-7]、個體采納閾值[8]等因素對謠言傳播產生的影響來拓展和改進SIR模型，但是這些研究都關注的是謠言向易感態用戶傳播時的特征，并沒有考慮節點開始恢復時的情況。

早在20世紀70年代，Rosnow等[9]就已經提出了謠言傳播的生命周期理論。在那之后各領域的學者都嘗試去研究謠言傳播周期中各個時期的特征并希望由此得到有效的謠言控制策略。任一奇等[10]針對國內社交媒體將網絡謠言分為產生、擴散、極化和消退四個階段， 并將謠言的消退分為了兩種類型：自然消退和人為消退。以官方辟謠為主的人為消退往往會因為傳播過程中出現的偏差或是一部分受眾產生逆反心理反而會促進謠言的擴散;而在自然消解的過程中，隨著周圍用戶參與到謠言傳播的比例增加，已參與到謠言傳播的用戶對謠言的了解也會逐漸增加直到因為接觸到事件真相或是失去興趣而停止對謠言的傳播。王理等[11]基于真實謠言信息樣本也對謠言消退的現象進行了實證研究。

在上述研究的基礎上，本文首先根據謠言生命周期理論中謠言消退期的特點對SIR傳播模型進行改進，引入鄰居節點狀態對于易感態節點的影響，使得謠言消退的過程更加符合真實情況。接下來，為了可以定量地研究所提出的謠言傳播模型，本文拓展了一套異質邊劃分方法用于研究各個網絡結構參數和傳播模型參數對于謠言傳播的影響，得到不同條件下謠言最終傳播范圍和爆發閾值。最后，對謠言傳播模型進行進一步分析，并提出可以有效控制謠言傳播的免疫策略。

1?謠言傳播模型概述

假設謠言在節點數量為N、度分布為 P（k）的復雜網絡上傳播。網絡中的每一個節點可以處于以下三種可能狀態中的一種：1）節點不知道流言的無知態（gnorant）;2）節點開始傳播謠言的傳播態（spreader）;3） 節點不再傳播謠言的恢復態（refractory）。在每個時間步中，每個具有度k′的 spreader 節點v首先嘗試向所有它的鄰居節點傳遞謠言。如果 spreader節點v的鄰居中有一個無知態節點u，那么u以概率λ接受謠言并成為一個新的傳播態節點。在謠言消退時傳播態節點需要其鄰居節點提供與謠言有關的信息來識破謠言進而對謠言失去興趣，因此，在模型中傳播態節點v以概率1-（1-γ）nk′變成恢復態節點，其中nk′是其鄰居中傳播態節點和恢復態節點的數量之和，γ是節點v鄰居中只有一個傳播態或恢復態節點時v變為恢復態的概率，在本文中被稱作基礎恢復概率。當系統中不再有傳播態節點時，傳播過程結束。謠言傳播模型整體架構如圖1所示，無知態節點每個時間步以概率λ轉為傳播態節點，傳播態節點每個時間步以概率1-（1-γ）nk′轉變為恢復態節點。

2?基于異質邊劃分的理論分析

謠言的最終傳播范圍和傳播的爆發閾值是運用復雜網絡研究謠言傳播動力學特征時的兩個重要的目標。謠言傳播范圍是指當謠言傳播結束時網絡中參與到謠言傳播的節點比例。受到文獻[12]的啟發，本章擴展了一套異質邊劃分方法，用于對本文提出的謠言傳播模型的傳播范圍進行分析。記S（t）、I（t）、R（t）分別表示在t時刻，處于傳播態、無知態和恢復態節點的比例，并滿足S（t）+I（t）+R（t）=1。參考空穴理論[13-14]，令任意節點u處于空穴態，即u不能感染鄰居節點，但是可以被鄰居節點感染。記θk′（t）表示度為k′的某鄰居節點直到 t 時刻，仍然沒有通過兩點之間的邊感染節點u的概率。在異質網絡中，節點通常具有不同大小的度，不同度的節點θk′（t）取值也有所不同。考慮鄰居節點所有可能的度取值，記θ（t）為u節點截止t時刻仍然沒有被某個鄰居感染的概率：

θ（t）=∑k′=0k′P（k′）〈k〉 θk′（t）（1）

其中〈k〉為網絡的平均度。對于網絡中的任意一個節點來說，設i（k，t）為t時刻度為k的節點為無知態的概率：

i（k，t）=θk（t） （2）

考慮k所有可能的取值，可以得到t時刻網絡中無知態節點的比例：

I（t）=∑k=0P（k）i（k，t） （3）

根據θk′（t）的定義，可以將其分為3個部分：

θk′（t）=ξIk′（t）+ξSk′（t）+ξRk′（t） （4）

其中：ξIk′（t）、ξSk′（t）和ξRk′（t）分別表示，度為k′的節點處于無知態、傳播態和恢復態，并且截止t時刻沒有感染鄰居的概率。

當節點v處于無知態時，v不能傳遞謠言給鄰居u，滿足ξIk′（t）的定義，因此v處于無知態的概率與ξIk′（t）相等。由于u處于空穴態，它也不能傳染v，因此，v只能被其余k′-1個鄰居感染。可以由此得到進一步可以由定義得到 v 處于無知態的概率：

ξIk′（t）=θk′-1（t）（5）

根據θk′（t）的定義，當度為k′的節點v通過一條邊感染鄰居u時，θk′（t）將會減小。節點v感染節點u需要滿足兩點：1）節點v截止t時刻之前處于傳播態并且沒有感染u節點;2）在t時刻，節點v通過兩點之間的邊以概率λ感染節點u。 由此可以得到θk′（t）的演化方程：

dθk′（t）dt=-λξSk′（t）（6）

傳播態節點v的恢復概率與該時刻v鄰居節點中傳播態節點和恢復態節點的數量有關，設nk′為v鄰居中傳播態節點和恢復態節點的數量之和。對于某個度為k″的v的鄰居來說，在t時刻處于無知態的概率為θk″（t），由此可以進一步得到度為k″的v的鄰居在t時刻處于傳播態的概率和處于恢復態的概率之和為1-θk″（t）。考慮k″所有可能的取值，可以得到某個v的鄰居處于傳播態或是恢復態的概率為∑k″=0k″P（k″）〈k〉[1-θk″（t）]。空穴態節點u不會感染節點v，因此v的鄰居中一定還存在一個之前感染v的傳播態節點或是恢復態節點。由此可以得到nk′：

nk′=1+（k′-2）∑k″=0k″P（k″）〈k〉[1-θk″（t）]（7）

根據定義，當滿足下面三個條件時，ξRk′會在t時刻增加：1）傳播態節點v截止t 時刻之前沒有通過兩點之間的邊將謠言傳給節點u，根據定義可以知道這個條件的概率就是ξSk′（t）;2）傳播態節點v在t 時刻沒有通過兩點之間的邊將謠言傳給節點u，概率為（1-λ）;3）傳播態節點v 在t 時刻以概率1-（1-γ）nk′恢復為恢復態。基于上述分析，可以得到ξRk′的演化方程：

dξRk′（t）dt=[1-（1-γ）nk′]（1-λ）ξSk′（t） （8）

式（4）～（8）聯立求解即可得出θk′（∞），當t→∞時，傳播過程結束，此時所有傳播態節點均已恢復為恢復態，因此S（∞）=0。通過代入t→∞來得出θk′（∞），進而可以得到傳播范圍R（∞）=1-I（∞）。

3?傳播爆發閾值分析

得到謠言爆發閾值是研究謠言在復雜網絡上傳播時另一個重要的目標，傳播爆發閾值可以被看作一個傳播概率上的臨界值，當傳播概率小于它時，謠言的最終傳播范圍趨近于0，否則會有一定比例的節點參與到謠言的傳播中。

3.1?理論閾值

針對理論計算得到的傳播范圍曲線，依據爆發閾值點處的特征可以使用導數法來求得曲線上的傳播爆發閾值點[15]，即傳播范圍的曲線在爆發閾值點處存在一階導數但不存在二階導數。

定義f1（λ）為傳播范圍函數R的一階導數：

f1（λ）=limΔλ → 0R（λ+Δλ）-R（λ-Δλ）2Δλ（9）

在爆發閾值點處，R（λ）不存在二階導數，也就是說在該點R（λ）的二階左導數與二階右導數不相等。因此定義P（λ）：

P（λ）=

|limΔλ → 0+f1（λ+Δλ）-f1（λ）Δλ-

limΔλ→0-f1（λ）-f1（λ-Δλ）Δλ|（10）

在爆發閾值處，P（λ）的值會呈現出峰值。

3.2?模擬閾值

可變性是一種用來確定磁性系統中的平衡臨界點的標準方法[16]。Shu等[17]提出可以利用可變性方法來確定SIS傳播模型和SIR傳播模型的模擬閾值，其表達式為：

Δ=〈ρ2〉-〈ρ〉2〈ρ〉（11）

Δ的值會在爆發閾值處呈現出峰值。

4?實驗分析

近年來針對真實世界的網絡進行的研究發現，大多數真實網絡都是稀疏網絡且度分布呈現出胖尾現象，即度分布服從冪率分布[18-19]，因此，仿真實驗分別在網絡規模設為N=10-000的ER網絡（ErdsRényi network）和無標度網絡上進行。為了使實驗網絡更加接近真實的網絡結構，根據相關研究[18-19]將網絡參數設置如下：ER網絡平均度〈k〉=10、最大度kmax～N，無標度網絡度分布指數為2.5和3.5。模擬的初始傳播態節點為5個，相同的模擬在每個網絡上重復10-000 次，并通過取平均值得到最后的結果。

首先，圖2將本文提出的謠言傳播模型和經典的SIR模型進行了對比，圖中S（t）表示傳播態節點（即SIR模型中的感染態節點）在網絡中所占比例，t表示傳播的時間步。從圖2中可以發現，S（t）在達到頂點之后會隨著網絡中接受謠言的節點數的增加而快速降低，與SIR模型相比，本文提出的謠言傳播模型傳播周期更短，爆發速度快但傳播規模會隨著參與傳播的人數和有關信息的累積而快速下降。謠言傳播模型這樣的特性比SIR模型更加符合謠言生命周期理論中網絡謠言消退期的特點[9-11]。

圖3、4分別研究了謠言在異質性較弱的ER網絡和異質性較強的無標度網絡上的傳播情況，圖中的線條圖表示傳播理論計算值，形狀圖表示傳播模擬值，理論值與模擬值能夠很好地吻合。

從第1章可知，傳播概率為λ，恢復概率為1-（1-γ）nk′， 其中基礎恢復概率γ是鄰居中傳播態節點或恢復態節點只有一個時的恢復概率。從圖3、4中可以發現，在傳播概率λ相同的情況下，最終的傳播范圍R（∞）會隨著傳播概率λ的增加而增大;爆發閾值則會隨著基礎恢復概率γ的增大而減小。

為了求出謠言在網絡上的傳播閾值，在圖5（a）、圖6（a）和（c）中，通過導數法求出謠言模型分別在ER網絡和無標度網絡上的理論閾值; 在圖5（b）、圖6（b）和（d）中，通過求可變性的方法得到謠言模型相應的模擬閾值。模擬謠言的一次傳播過程中，在傳播概率λ較小時可能會出現在傳播前期大部分傳播態節點還未將謠言傳播出去就轉為恢復態，導致謠言未能擴散而提前終止傳播的情況，因此傳播概率較小時多次模擬實驗結果求平均之后得到的模擬傳播范圍會稍微小于理論值，從而使得模擬爆發閾值會比理論值大0.01左右。 例如在圖5中基礎恢復概率γ為0.5時理論閾值為0.113，而模擬閾值為0.123。

通過上面的分析，可以得知傳播概率λ和基礎恢復概率γ都會影響到最終的傳播范圍R（∞）和爆發閾值。 圖7（a）和（b）分別展示了在平均度〈k〉為10的ER網絡上，最終傳播范圍R（∞）隨傳播概率λ和基礎恢復概率γ變化的理論結果和模擬結果。從圖中可以發現，最終的傳播范圍R（∞）隨傳播概率λ和基礎恢復概率γ的增大而增大，且理論值能很好地與模擬值吻合。

在圖7中，謠言在ER網絡上的傳播平面被分為了兩個區域：Ⅰ區域上謠言大規模爆發，即系統處于活躍態;Ⅱ區域上謠言只在很有限的范圍內傳播，即系統處于非活躍態（吸收態）。 圖中的白線就是在第三章中求出的閾值，可以發現，隨著基礎恢復概率γ的增加，爆發閾值λc會隨之減小。

在圖8中研究在無標度網絡上，不同的度分布指數α下，最終的傳播范圍R（∞）隨傳播概率λ對謠言傳播的影響。圖8（a）和（b）分別展示了在度分布指數α為2.5的無標度網絡上最終的傳播范圍R（∞）隨傳播概率λ和基礎恢復概率γ變化的理論值和模擬值。圖8（c）和（d）分別展示了在度分布指數α為3.5 的無標度網絡上最終的傳播范圍R（∞）隨傳播概率λ和基礎恢復概率γ變化的理論值和模擬值。

從圖8中可以發現，最終的傳播范圍R（∞）隨傳播概率λ和基礎恢復概率γ的增大而增大。 同樣的，爆發閾值將傳播平面分為了兩個區域：Ⅰ區域上謠言大規模爆發，即系統處于活躍態;Ⅱ區域上謠言只在很有限的范圍內傳播，即系統處于非活躍態（吸收態）。 當傳播概率λ和基礎恢復概率γ固定，最終的傳播范圍R（∞）和爆發閾值λc會隨著度分布指數α增加而變大，這意味著強異質性的網絡會有更小的爆發閾值。

5?基于邊的免疫策略

以上討論了謠言傳播模型的邊劃分理論分析和實驗模擬驗證，下面將對謠言傳播模型進行進一步分析，給出控制謠言傳播的免疫策略。

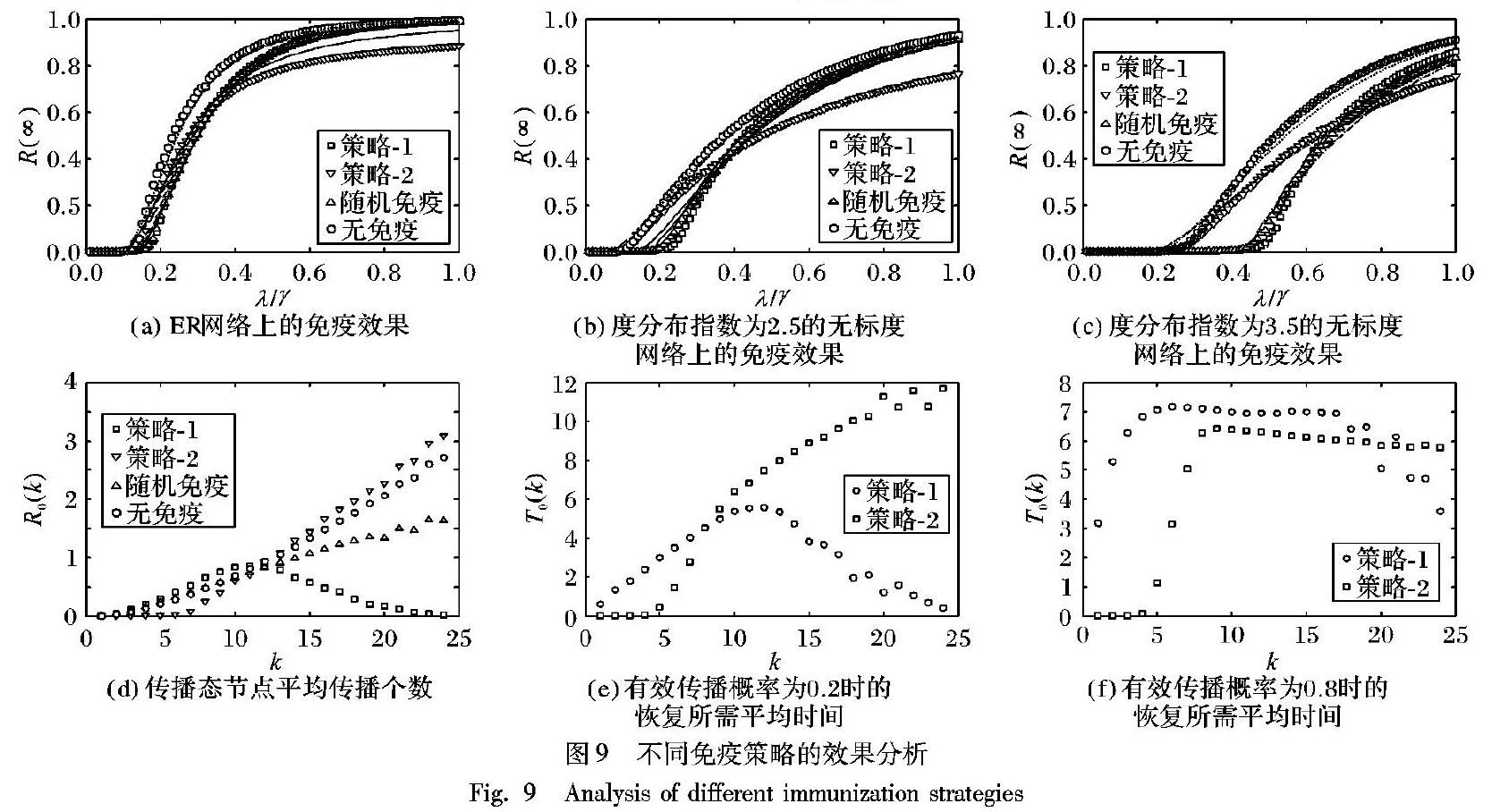
免疫是控制謠言在網絡中散布的有效方法，而根據網絡的特性使用有效的免疫策略對于控制謠言的散布可以起到更好的作用。為了有效地控制疾病或是輿情的傳播，學者們已經基于復雜網絡提出了一些經典的免疫策略，比如隨機免疫[20]、目標免疫和熟人免疫[21]以及基于著色的免疫[22]等策略。這些免疫策略都是針對網絡中的節點進行免疫，這類策略雖然可以得到很好的免疫效果，但是在免疫過程中刪去大度節點會極大地破壞網絡的原有結構和連通性。此外，在現實的社交網絡中，也很難能夠做到將一個用戶完全從網絡結構中去除。基于這種情況，Zhang等[23]提出了針對網絡中的邊進行免疫的策略，通過刪除網絡中關鍵的連邊可以有效地控制疾病或是輿情在網絡上的傳播。在上述的研究基礎之上，本文提出了一套基于刪邊的免疫策略來達到控制謠言傳播的目的。在這里假設網絡規模為N，免疫比例為f，則在初始時，網絡中有f·N條邊處于免疫狀態，即謠言不能通過這條邊傳播。

首先，對于網絡中的度為k1的節點u和度為k2的節點v之間的邊，用I（u，k）來表示節點u和節點v的度乘積，即k1·k2。接下來提出兩種免疫策略，并將兩者與現有的隨機免疫策略進行對比：策略1，優先免疫網絡中兩端節點度乘積I（u，k）較大的f·N條邊，謠言將不會通過這些邊傳播;策略2，優先免疫網絡中兩端節點度乘積I（u，k）較小的f·N條邊，謠言將不會通過這些邊傳播; 隨機免疫策略：隨機免疫網絡中f·N條邊，謠言將不會通過這些邊傳播。

按照上述的生成規則生成一個節點個數N=10-000的網絡。令網絡中的每個節點都處于無知、傳播、免疫這三種狀態中的一種狀態，采用第1章描述的謠言傳播模型，在t=0時刻，在網絡中隨機選擇5個節點作為傳播種子，然后根據不同免疫策略，選擇f·N條邊作為被免疫的邊（謠言不能通過該邊傳播），剩下的全為無知態節點。t=1時刻，謠言開始傳播，令R（∞）表示謠言最終的傳播范圍。 實驗分別在平均度為10的ER網絡、度分布指數為2.5和3.5的無標度網絡上進行，實驗結果是在這些網絡上模擬10-000次后取平均值得到的。 謠言傳播模型的參數γ設置為0.5。

為了對三種免疫策略的效果進行進一步的定量分析，還定義了參數R0（k），R0（k）表示所有度為k的感染態節點u在轉變為恢復態之前感染的鄰居節點個數的平均值，可以反映出不同度的節點對于謠言傳播的貢獻。圖9（d）表示了在仿真結果上三種免疫策略對于R0（k）的影響，可以發現：策略1可以有效限制謠言在大度節點之間的傳播;類似的，策略2可以有效限制謠言在小度節點之間的傳播。

圖9（a）、（b）和（c）分別研究了在不同結構的網絡上，不同的免疫策略對謠言傳播行為的影響。通過觀察這三個圖可以發現，與現有的隨機免疫策略相比，當有效傳播概率λ/γ較小時，優先免疫I（u，k）較大的邊的策略1對比隨機免疫策略可以更加有效地降低最終傳播范圍R（∞）。而隨著有效傳播概率λ/γ的增長，采用優先免疫I（u，k）較小的邊的策略2對比隨機免疫策略會有更好的效果，這個結果表明策略1和策略2在各自的有效區間上的免疫效果均超過了經典免疫策略。接下來針對策略1和策略2在免疫效果上出現的交叉現象進行進一步的分析。首先定義參數T0（k），T0（k）表示網絡中度為k的節點參與到謠言傳播中的平均時間步長度，這個參數可以一定程度上反映出不同度節點識破謠言所需的平均時長，分別在有效傳播概率λ/γ為0.2和0.8時統計T0（k）隨k的變化情況。

圖9（e）表示了當基礎恢復概率γ固定為0.5且有效傳播概率λ/γ為0.2時T0（k）隨k的變化情況， 此時有效傳播概率λ/γ較小，謠言在網絡上的傳播相對較慢。在這種情況下，策略1有效減少了謠言在大度節點之間的傳播，避免了謠言通過大度節點擴大傳播范圍，使得謠言的在一個有限的范圍內傳播。而策略2減少的是謠言在小度節點之間的傳播，但謠言依然可以通過大度節點擴散，使得最終的傳播范圍大于策略1的結果。

圖9（f）表示了當基礎恢復概率γ固定為0.5且有效傳播概率λ/γ為0.8時T0（k）隨k的變化情況，此時有效傳播概率λ/γ較大，謠言更容易被節點接受，在網絡上的傳播也更加迅速。在這種情況下，策略1雖然免疫了大度節點之間的關鍵路徑，但由于謠言依然可以通過其他小度節點將謠言傳遞到大度節點處，因此策略1在此時效果不佳。此外，由于沒有對小度節點之間的傳播進行限制，謠言會快速傳播到了一些與外部連接較少的小度節點處，并且這類傳播態節點會因為參與謠言傳播的鄰居節點個數較少，收到有關謠言的信息有限從而需要更多的時間步來轉變成恢復態。策略2有效減少了謠言在小度節點之間的傳播，而大度節點附近的節點雖然會接收到謠言但也會因為有較多參與到謠言傳播中的鄰居節點而能夠較快地轉變為恢復態，因此在策略2下傳播態節點恢復所需的平均時間步要小于策略1時的情況。節點保持傳播態的時間步越短能夠傳播的謠言數量越少，因而在當有效傳播概率λ/γ較大時策略2有更好的免疫效果。

6?結語

本文基于謠言傳播的相關研究，根據社交網絡中謠言在消退期的特點對傳播動力學中的SIR傳播模型進行改進，并拓展了一套異質邊劃分方法用于得到傳播范圍和爆發閾值這兩個傳播動力學中的重要指標。之后對模型進行了理論分析和模擬仿真，說明了謠言消退期的特征對謠言在社交網絡上傳播的影響。在此基礎上提出了有效的謠言控制策略，并探討了有效傳播概率對不同策略免疫效果的影響。此外，社會傳播的加強效應以及更真實復雜的網絡結構對謠言傳播帶來的影響仍待進一步探究，未來擬對該方向進行進一步的研究。

參考文獻 （References）

[1]?KREINDLER G E， YOUNG H P. Rapid innovation diffusion in social networks[J]. Proceedings of the National Academy of Sciences of the United States of America， 2014， 111（S3）： 10881-10888.

[2]?WATTS D J， STROGATZ S H. Collective dynamics of ‘smallworld networks[J]. Nature， 1998， 393（6684）：440-442

[3]?BARAB?SI A L，ALBERT R. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）：509-512.

[4]?NEWMAN M E. Spread of epidemic disease on networks[J]. Physical Review E： Statistical Nonlinear & Soft Matter Physics， 2002， 66（1 Pt 2）： No.016128.

[5]?GLEESON J P. Cascades on correlated and modular random networks[J]. Physical Review E： Statistical Nonlinear & Soft Matter Physics， 2008， 77（4 Pt 2）： No.046117.

[6]?CENTOLA D. An experimental study of homophily in the adoption of health behavior[J]. Science， 2011， 334（6060）： 1269-1272.

[7]?DODDOS P S， WATTS D J. Universal behavior in a generalized model of contagion[J]. Physical Review Letters， 2004， 92（21）： No.218701.

[8]?KARIMI F， HOLME P. Threshold model of cascades in empirical temporal networks[J]. Physica A： Statistical Mechanics & Its Applications， 2013， 392（16）： 3476-3483.

[9]?ROSNOW R L， FINE G A. Rumor and gossip： the social psychology of hearsay[J]. Canadian Journal of Sociology， 1977， 22（5）： 212-214.

[10]?任一奇，王雅蕾，王國華，等. 微博謠言的演化機理研究[J]. 情報雜志， 2012， 31（5）： 50-54. （REN Y Q， WANG Y L， WANG G H， et al. Research on the Evolution Mechanism of Microblog Rumors[J]. Journal of Intelligence， 2012， 31（5）： 50-54.）

[11]?王理，謝耘耕. 公共事件中網絡謠言傳播實證分析——基于2010～2012年間網絡謠言信息的研究[J]. 上海交通大學學報（哲學社會科學版）， 2014， 22（2）： 86-99. （WANG L， XIE Y G. An empirical analysis online rumors in public events — based on the data of online rumors from 2010 to 2012 [J]. Journal of Shanghai Jiaotong University： Philosophy and Social Sciences， 2014， 22（2）： 86-99.）

[12]?MILLER J C， VOLZ E M. Model hierarchies in edgebased compartmental modeling for infectious disease spread[J]. Journal of the Royal Society Interface， 2013， 67（4）： 869-899.

[13]?KARRER B， NEWMAN M E J. Message passing approach for general epidemic models[J]. Physical Review E： Statistical， Nonlinear & Soft Matter Physics， 2010， 82（1 Pt 2）： No.016101.

[14]?KARRER B， NEWMAN M E J， ZDEBOROV??L. Percolation on sparse networks[J]. Physical Review Letters， 2014， 113（20）： No.208702.

[15]?RADICCHI F. Percolation in real interdependent networks[J]. Nature Physics， 2015， 11（7）： 597-602.

[16]?FERREIRA S C， FERREIRA R S， CASTELLANO C， et al. Quasistationary simulations of the contact process on quenched networks[J]. Physical Review E： Statistical， Nonlinear & Soft Matter Physics， 2011， 84（6 Pt 2）： No.066102.

[17]?SHU P， WANG W， TANG M， et al. Numerical identification of epidemic thresholds for susceptibleinfectedrecovered model on finitesize networks[J]. Chaos， 2015， 25（6）： No. 063104.

[18]?NEWMAN M. Networks： an Introduction[M]. Oxford： Oxford University Press， 2010：661-703.

[19]?VIRKAR Y， CLAUSET A. Powerlaw distributions in binned empirical data[J]. The Annals of Applied Statistics， 2014， 8（1）： 89-119.

[20]?PASTORSATORRAS R， VESPIGNANI A. Immunization of complex networks[J]. Physical Review E： Statistical， Nonlinear & Soft Matter Physics， 2002， 65（3 Pt 2A）： No.036104.

[21]?REUVEN C， SHLOMO H， DANIEL B A. Efficient immunization strategies for computer networks and populations[J]. Physical Review Letters， 2003， 91（24）：No. 247901.

[22]?黃斌，趙翔宇，齊凱，等. 復雜網絡的頂點著色及其在疾病免疫中的應用[J]. 物理學報， 2013， 62（21）： No.218902. （HUANG B， ZHAO X Y， KAI Q， et al. Coloring the complex networks and its application for immunization strategy[J]. Acta Physica Sinica， 2013， 62（21）： No.218902.）

[23]?ZHANG H， LI K， FU X， et al. An efficient control strategy of epidemic spreading on scalefree networks[J]. Chinese Physics Letters， 2009， 26（6）： 298-301.

LUO Jingyu， born in 1995， M. S. candidate. His research interests include complex network， machine learning.

TANG Ningjiu， born in 1960， Ph. D.， professor. His research interests include software engineering， complex system.