關于一元多項式的Casas-Alvero猜想一類情況研究

楊環瑜

（湛江幼兒師范專科學校，數學系，廣東 湛江 524084）

一、引言

（一）本文背景

自1998 年Casas-Alvero（巴塞羅那大學數學系教授）提出Casas-Alvero 猜想以來[1]，該猜想一直受到了數學界人士的青睞，該猜想在拓撲學中有極其廣泛的應用。Casas-Alvero教授和多位數學家致力于證明該猜想的正確性，希望能證明這一點。因此，至今這個問題仍然沒有解決，現在被稱為Casas-Alvero猜想。本文將運用高等代數知識討論有關復系數一元多項式的Casas-Alvero猜想。

（二）國內外研究現狀

近年來，研究人員對Casas-Alvero 多項式的研究是數學界熱門的話題之一。2005 年，Diaz-Toca G.M.和Gonalez-Vega L.能夠證明的猜想度最高到8（公布到7），使用了重計算方法[2]。

隨后，Von Bothmer H.-C.G.，Labs O.，Schicho J.和van der Woestijne C，證明這一猜想的度是素數冪以及其他一些相關情況［3］。

Draisma J.和De Jong J.P.給出了當前問題的不同證明和一個不錯的關于猜想的介紹，使用了估值理論去證明而不是代數幾何方法［4］。

（三）本文主要內容及其意義

設f(x)是形如

的首項系數等于1的n（n ＞1）次復系數一元多項式,又設f(k)(x)(k=1,···,n-1)是f(x)的k階導數，如果存在復數α1,···,αn-1可使

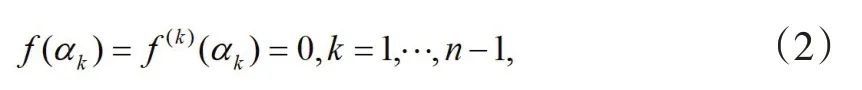
則稱f(x)是n次Casas-Alvero多項式。2001年，E.Casas-Alvero[1]在研究平面曲線的拓撲性質時定義了此類多項式，并且提出以下猜想：

猜想A如果f(x)是n次Casas-Alvero多項式，則必有：

其中α是復數。

上述的猜想A稱為Casas-Alvero 猜想，這是一個迄今尚未解決的難題，目前只證實了一些極特殊的情況［2］-［4］。例如，當多項式f(x)的次數n＜12 時猜想A成立，但是現在還不知道該猜想在n=12時是否成立［3］。

由復系數一元多項式的因式分解定理可知:如果f(x)適合(3)，則f(x)僅有根x=α；反之，任何有不同根的多項式都不能表成（3）之形［5］。因此，猜想A可等價地表述為：

猜想B如果f(x)有不同的根,則f(x)不是Casas-Alvero多項式。

由此可知：若能證明任何有不同根的多項式都不是Casas-Alvero多項式，則即可斷定Casas-Alvero猜想成立。根據以上思路，本文解決了Casas-Alvero猜想的一類基本情況，即證明了以下定理。

主要結果：

定理如果f(x)恰有2個不同的根，則f(x)不是Casas-Alvero多項式。

上述定理的證明要用到一元多項式的下列性質。

二、一些引理

引理1［5］如果重根的個數按重數計算，則n 次復系數一元多項式恰有n個根。

引理2［5］當n 次多項式f(x)可表成（1）時，如果α1,…,αn是f(x)的n個根，則。

引理3［5］x0是f(x)的k 重根的充分必要條件是f(x0)=f'(x0)=…=f(k-1)(x0)=0，而f(k)(x0)≠0。

引理4［8］如果是形如（1）的多項式的所有不同的根，分別是它們的重數，則

引理5［9］對于形如（1）的多項式f(x)，設未定元y與x適合

引理6［5］復系數n(≥1)次多項式在復數域上都可唯一地分解成一次因式的乘積。

三、定理的證明

（一）思路的來源

該猜想涉及多項式的根、多項式理論以及多項式的n階導數；通過查詢資料，發現現有的相關研究極其有限，所以只能從多項式的基本特征入手，靈活運用“高等代數”等專業課程知識。非常幸運的是，引理3與該猜想的相關條件非常相似，故本人選擇從引理3 尋找突破口，獲得方法去證明該猜想的正確性。

（二）定理的證明

設f(x)是形如（1）的n次復系數一元多項式，又設f(x)恰有2個不同的根α和β，它們的重數分別是n1和n2，此時，α和β是適合

的復數；根據引理1可知n1和n2是適合

的正整數;又從引理2可知

根據一元多項式的求導法則（參見文［5］），可知f(x)的n-1階導數是

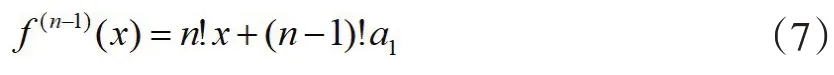
如果f(x)是Casas-Alvero多項式，則從此類多項式的定義（2）可知：存在復數αn-1適合

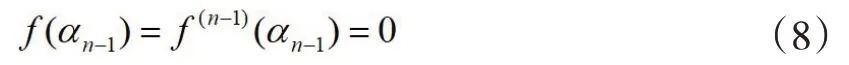
從（9）可得

（10）代入（8）可知

或者

當（12）成立時，從（6）可得

結合（5）和（14）可得

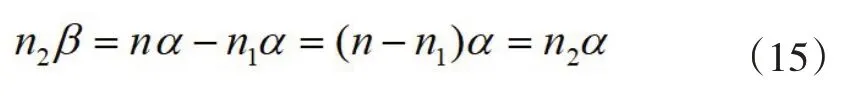
由于n2是正整數，所以從（15）可得α=β 這一與（4）矛盾的結果。

同理可證：當（13）成立時，亦可得α=β 這一矛盾。

綜上所述可知：當f(x)恰有2個不同的根時,f(x)不是Casas-Alvero 多項式，定理證完。

（三）定理的應用

解法1（矩陣的初等行變換法）：

顯然，f(x)恰好有兩個根-1 和4，故由上述定理直接可以判斷，f(x)不是Casas-Alvero多項式。

解法2（行列式法）：

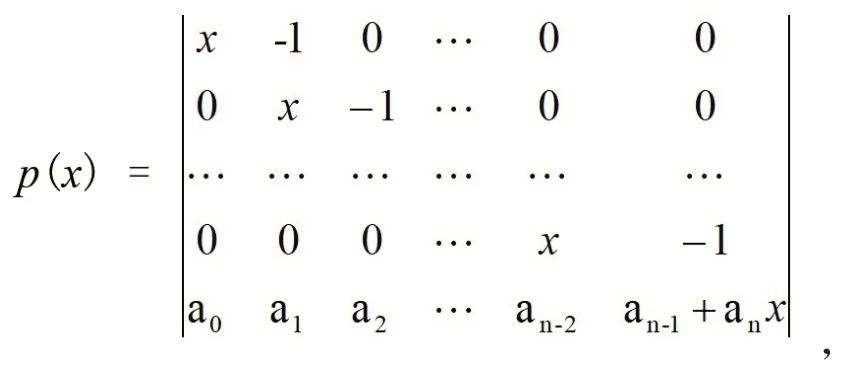
利用行列式的性質，通過降階和提取公因式的方法進行因式分解[7]。

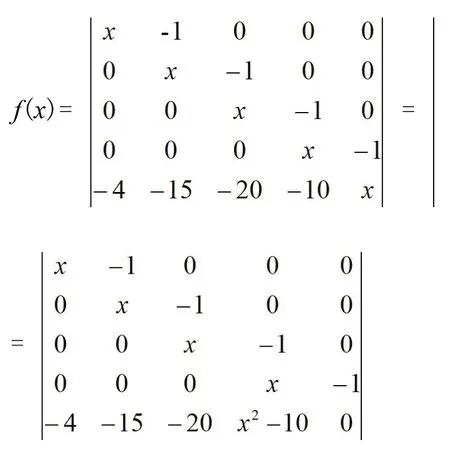
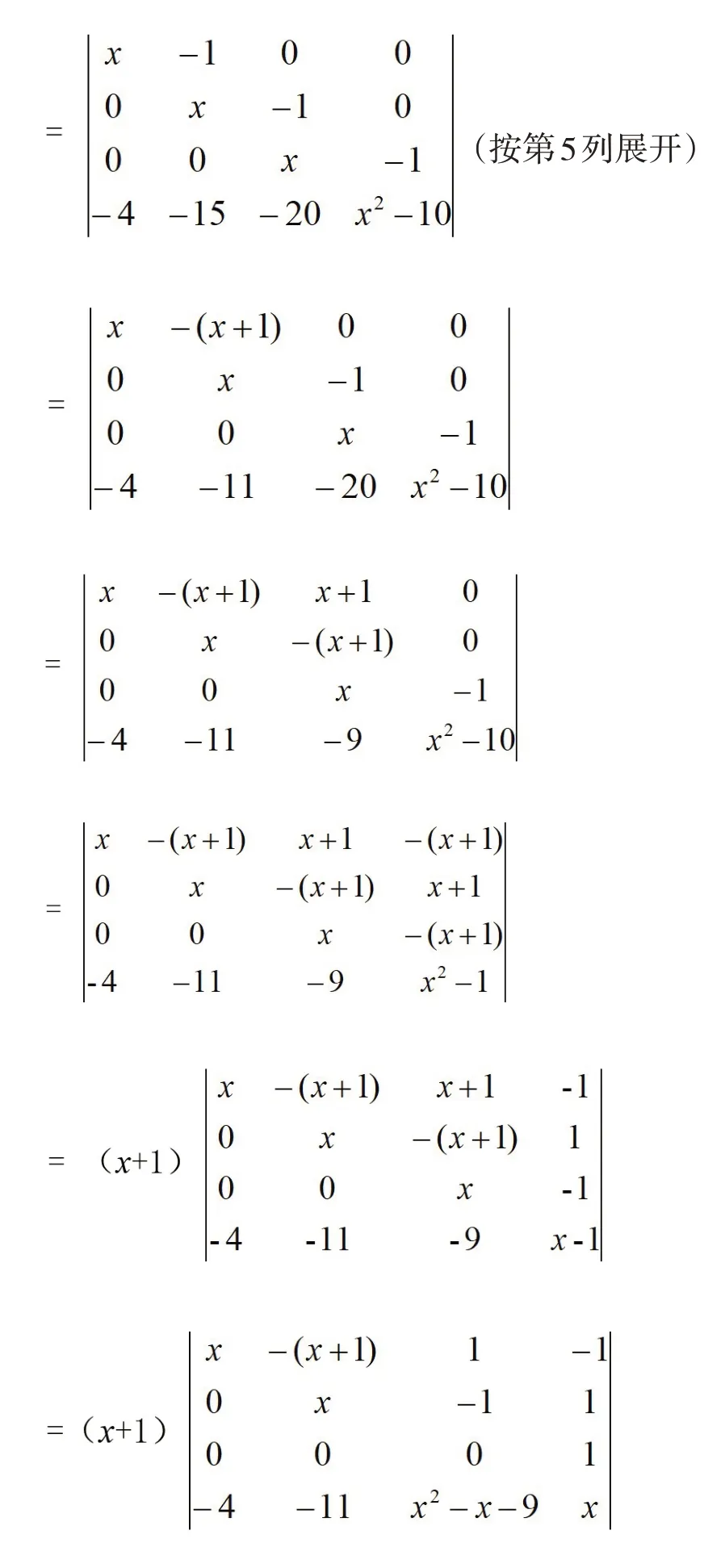
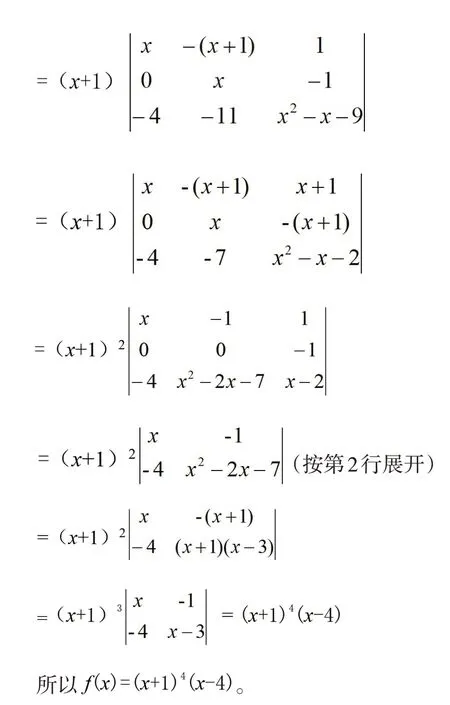
顯然，f(x)恰好有兩個根-1 和4，同理由定理直接可得：f(x)不是Casas-Alvero多項式。