含Lugre動摩擦及間隙的振動系統的動力學分析

張艷龍，李振國，王 麗

（1.蘭州交通大學 機電工程學院，蘭州730070； 2.蘭州城市學院 數學學院，蘭州730030）

含間隙的機械構件廣泛存在于交通、航天、航空等機械系統中，在這類機械構件運轉過程中或其他外激勵作用下，一些零部件間將出現碰撞和摩擦，并引起噪聲、振動等，將會更進一步導致效率降低甚至設備的損壞。因此多年來許多國內外學者通過建立不同的力學模型和摩擦模型來研究摩擦導致的黏滑、顫振及分岔行為。文獻[1-2]利用含有干摩擦的Filippov 振動系統來研究滑移分岔和混沌動力學行為。文獻[3]研究一種具有庫倫干摩擦的振動驅動系統，分析其雙參數分岔問題，并解釋了滑移、黏滯等運動狀態之間的轉換，利用系統的黏特性對系統進行了優化。文獻[4]建立一類含單邊約束的2自由度塑性碰撞振動系統，研究參數變化、分段特性和擦邊奇異性對系統的影響，分析了顫振碰撞發生的條件以及不同周期運動下的顫振運動現象。文獻[5]通過研究三模塊振動系統，分析非對稱庫侖干摩擦模型對振動驅動機械系統動力學行為的影響。周鵬等[6]建立干摩擦條件下含雙側約束的2 自由度塑性碰撞振動系統動力學模型，研究系統中存在的黏滑、滑動及碰撞等動力學行為。錢大帥等[7]利用諧波平衡法研究干摩擦振子雙黏著運動響應的級數解并對黏滑邊界進行了分析。丁旺才等[8]通過對含對稱間隙的摩擦振子的非線性動力學行為的研究，闡述了該系統在運動過程中存在的叉式分岔、對稱運動及反對稱運動等。上述文獻皆通過考慮靜摩擦模型或者相關的解析法來研究不同的含間隙及碰撞振動系統。

但在實際工況中，為了更加準確描述含摩擦系統的動力學行為，很多文獻考慮在不同的含摩擦系統中引入本身就具有動力學特性的動摩擦模型來研究，比如Dankowicz 動摩擦模型[9-10]、Lugre 動摩擦模型[11-13]以及改進Lugre 動摩擦模型[14]，這些動摩擦模型從微觀方面去解釋摩擦力，其摩擦力不僅與物體運動速度和正壓力有關，還和運動物體與接觸面之間的內部變量（如兩物體接觸表面的平均形變）有關。為了研究滾子軸承實際工作過程中的動力學特性，將引入Lugre動摩擦模型（既可描述摩擦過程中的靜態特性，也可描述其動態特性），來研究簡化出的含摩擦及間隙的兩自由度碰撞振動系統，并對該系統各個運動階段進行理論分析，通過數值仿真分析，研究系統運動過程中由于間隙碰撞及摩擦引起的顫振等非線性動力學特性對系統穩定性的影響，從而為系統安全可靠性及相關機械構件的優化設計等提供相關的理論基礎。

1 系統模型及運動狀態

圖1 單列圓柱滾子結構示意圖

圓柱滾子在運轉過程中會與保持架中滾子所處的隔離塊兩側發生碰撞，從而產生顫振等動力學行為。為研究其運轉過程中發生的碰撞及顫振等動力學特性，將該單列圓柱滾子軸承力學模型簡化為一類含摩擦及間隙的兩自由度碰撞振動系統，如圖2所示。

圖2 含摩擦及間隙碰振系統模型簡圖

其中滾子用質量為M1的振子1表示。保持架的部分用質量為M2的振子2 表示，將隔離塊兩側和保持架及阻尼油分別簡化為相連的剛度系數為K1、K2和K3的線性彈簧及阻尼系數為C1、C2的線性阻尼器，振子1 與振子2 之間為光滑接觸，振子2 與固定面之間為非光滑接觸，假設阻尼是Rayleigh 型比例阻尼，碰撞過程由碰撞恢復系數R確定，簡諧激振力Psin(ΩT+τ)作用在振子M1上，振子M1和振子M2的位移分別用X1和X2表示。

系統運動微分方程為

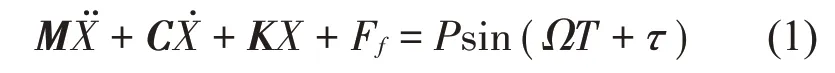
式中：

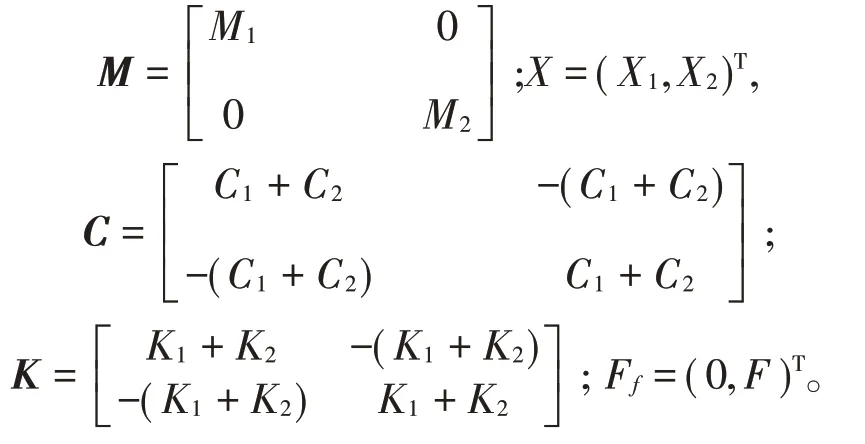
無量綱后的系統參數及變量如下

有學者認為在微觀狀態下，兩個相互接觸物體的接觸面通過彈性剛毛接觸，通過切向力作用，使得接觸面間的剛毛發生形變而產生相應的摩擦力，當該彈性形變達到一定程度時，兩個物體就會發生相對運動。

半個學年過去了，我是越戰越勇，名次上升很快，甚至數學還以滿分和張紹凡并駕齊驅。她看我的眼神變得不一樣了，有驚奇還有疑惑。

無量綱后Lugre摩擦模型的數學描述為

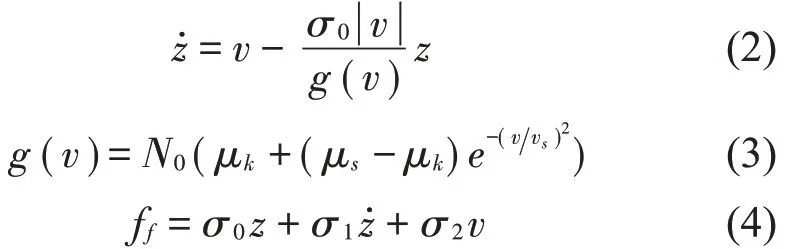
式中：無量綱量z表示剛毛平均形變；v表示接觸面相對速度；N0表示正壓力；vs表示Stribeck速度；μs表示靜摩擦系數；μk表示最小動摩擦系數；σ0、σ1、σ2分別表示剛度系數、阻尼系數和黏滯系數；ff為摩擦力。

在完整的系統運動過程中，將產生3 種不同性質的運動狀態：

(1)振子1 和振子2 同時處于運動狀態，即滑移階段；

(2)振子1 處于運動狀態，振子2 處于粘著靜止狀態；

(3)由于兩側存在約束，當振子1 與振子2 的位移差等于間隙b時，兩者發生碰撞，即碰撞階段。

可見，振子2的將會在滑移、粘著與碰撞三者運動狀態之間相互轉換，這使得其運動過程變得較為復雜。現將該系統的運動過程劃分為如下階段進行討論：

階段1：滑移段

因為有簡諧激勵力作用在振子1上，故振子1的狀態始終是運動的，而振子2 所受的力則為通過振子1 作用在振子2 上的力，該力為振子2 的驅動力，即若振子2 受到的力大于振子2 所受彈簧3 的彈性力以及摩擦力，且同時振子2的速度不為零，即時，則 振子2 做加速滑移運動，即前滑段。此時，振子1 與振子2都處于運動狀態，系統運動狀態方程為

若振子2 所受到的力小于振子2 所受的彈簧3的彈性力及摩擦力，且同時振子2的速度不為零，即時，則振子2 做減速滑移運動，即后滑段。此時，振子1 與振子2都處于運動狀態，系統運動狀態方程為

階段2：粘著段

若滿足振子2 所受到的力小于振子2 所受彈性力及摩擦力，且同時振子2 的速度為零，即時，則振子2處于黏滯狀態。此時，振子1為運動狀態，振子2為黏滯狀態，系統運動狀態方程為

階段3：碰撞段

由于摩擦力的作用，系統在粘著狀態下不會發生碰撞，而在滑動狀態時，當振子1 與振子2 的位移滿足 ||x1-x2=b,則此時振子1 與振子2 發生碰撞，根據動量守恒定律及碰撞關系得

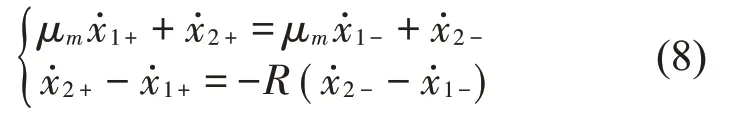
通過數值模擬對綜上所述的含間隙及摩擦的碰撞-振動系統的3 種運動階段進行動力學分析，由于對稱剛性約束碰撞振動系統在適當的系統參數條件下能夠呈現對稱型1-1-1周期運動，這里用n-p-q表示系統的周期碰撞運動，n表示力周期數，p和q分別表示振子1 與振子2 在擋板A 和C 的碰撞次數。為了研究摩擦碰撞振動系統的周期運動及分岔現象，選取Poincaré 截面建立Poincaré映射：

式中：X∈R4;v是實參數。

2 激振頻率對系統動力學行為的影響

事先通過選取多組系統參數對系統的動力學行為進行大量的數值仿真，發現選取如下系統參數：M1=0.1kg,M2=1.0 kg,K1=K2=4.44 N/m,K3=6.68 N/m,C1=C2=0.25 N ?s/m,ξ=0.5,vs=0.15,σ0=2 500,b=0.2,R=0.8,α=3.2,μk=0.5,μs=0.25,σ1=100,σ2=10，系統存在特定的分岔行為，如圖3所示。

進而分析Lugre 動摩擦對系統動力學行為的影響，由圖3可見隨著頻率ω的增大，系統總在混沌狀態與逆周期倍化分岔狀態之間相互轉換，在ω=12.77時，系統發生Hopf分岔，最后在ω＞13.34時，系統進入周期1穩定狀態。

圖4為系統在激振頻率ω取不同值時的相圖和時間歷程圖。如圖4(a)所示，當ω=13.34 時，系統呈現出非對稱的周期1-1-1 運動，隨著激振頻率的減小，系統從穩定的周期1 運動進入混沌狀態；在ω=7.0時，系統從混沌狀態進入周期1－2－2運動，相圖如4(b)所示，隨后又進入混沌狀態；當激振頻率減小到ω=5.1 時，系統進入周期1-3-3 運動，相圖如4(c)所示，在ω=4.9時,系統發生倍化分岔，隨后隨著激振頻率的遞減，系統又進入混沌狀態；當ω=4.0 時，系統又進入周期1-4-4 運動，相圖如4(d)所示，在ω=3.85時，系統又發生倍化分岔；隨著激振頻率的不斷遞減，系統在ω=3.3 和ω=2.7 時，分別由混沌狀態進入周期1-4-4運動和周期1-5-5運動，相圖如圖4(e)和圖4(f)所示，在ω變化期間，系統又經歷了由混沌狀態到倍化分岔以及由倍化分岔再到混沌狀態的改變。圖4(g)至圖4(h)所示的ω=13.34 時的時間歷程圖詳細描述了系統的運動過程。以碰撞前A點為起始點進行分析，系統開始由A點進入到碰撞階段，碰撞瞬間完成，速度發生突變，但位移未發生改變，到B點碰撞階段結束；此時系統由B點進入后滑段，速度逐漸降低，此時摩擦力小于驅動力，在CD段發生粘滑現象，速度、位移基本未發生變化；隨著力方向的變化，在驅動力大于摩擦力的瞬間，速度發生突變，但速度突變幅值較小，接近平滑過渡，E 點為粘滑現象結束點；此后由于系統受力方向和速度方向一致，因此在E 點進入前滑段，在F 點發生碰撞，前滑段結束，速度發生跳躍，G點為碰撞結束點，在GA段，由于力方向和速度方向的不斷變化，系統先進入后滑段，接著過渡到前滑段，到A點完成系統的一個周期運動。由于AB段為碰撞段，速度發生跳躍，但位移未發生改變，故在圖4(h)所示的位移-時間歷程圖中，A、B點是重合的，同理，E、F點也是重合的。

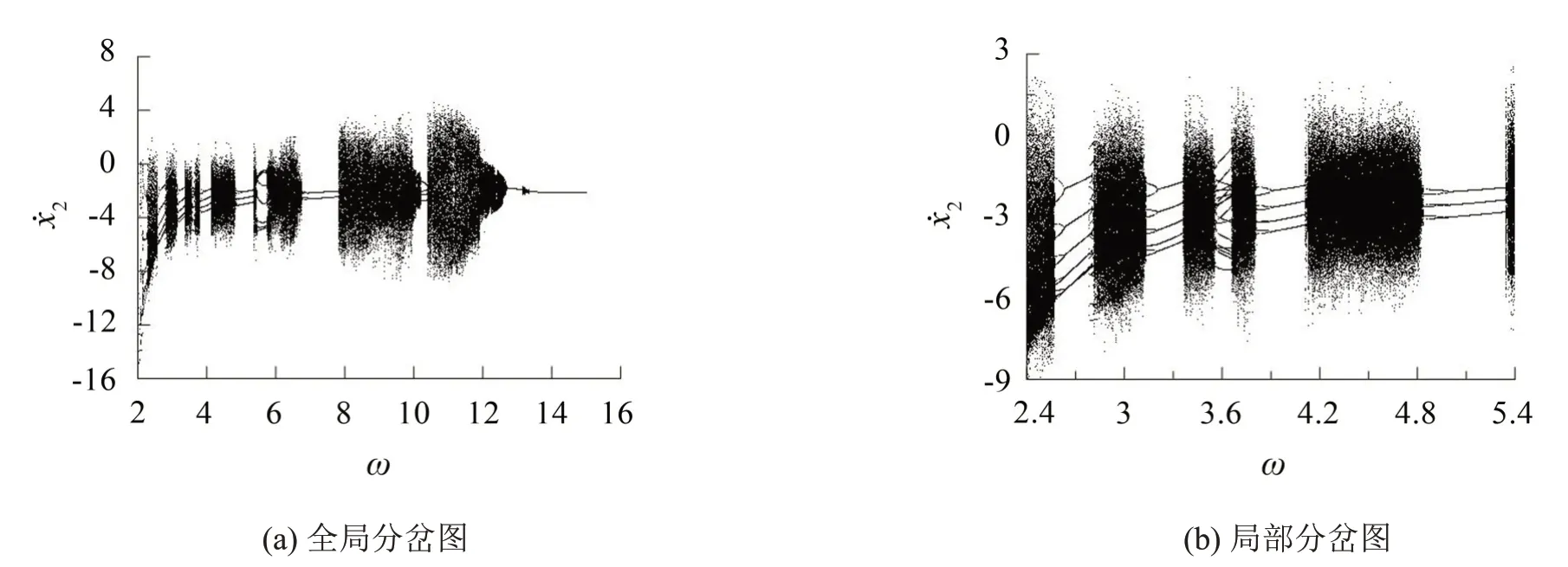
圖3 系統隨量綱-激振頻率的分岔圖

3 間隙對系統動力學行為的影響

選取大量參數進行數值仿真分析，為更加明顯表現系統的動力學特性，現選取系統參數如下：

M1=0.1kg,M2=1.0 kg,K1=K2=4.44 N/m,C1=C2=0.25 N ?s/m,K3=6.68 N/m,ξ=0.5,vs=0.15,σ0=3 000,ω=2.2,R=0.5,α=3.2,μk=0.5,μs=0.55,σ1=500，σ2=10。對該系統進行數值模擬，以滾子與隔離塊之間的間隙b作為分岔參數，分析其對系統動力學行為的影響，得到系統在不同激振頻率下的分岔圖如圖5所示，其中圖5(a)是當激振頻率ω=2.2時，得到的系統全局分岔圖，從圖中可以看出隨著間隙b的增大，系統由原先的混沌狀態逐漸進入逆周期倍化分岔狀態，同時在不斷的遞增過程中，又再次進入混沌狀態系統，隨后又發生逆周期倍化分岔以及后面的Hopf分岔，同時系統的運動周期也在逐漸減小；圖5(b)為圖5(a)的局部放大分岔圖，該圖可以更加清楚顯示系統在ω=2.2 時的分岔狀態。圖5(c)至圖5(d)分別為激振頻率ω=5.0 和ω=8.0 時的系統分岔圖，結合ω=2.2 時的分岔圖，可以看出將間隙b控制在一定的范圍內時，隨著激振頻率ω的增加，系統的運動周期會越來越小，直至最后的周期1 運動狀態。

4 結語

本文建立一類兩自由度含間隙及摩擦碰撞振動的系統動力學模型，根據實際情況，詳細分析了該系統的整個運動過程，列出系統在不同運動階段的判斷依據，并利用數值仿真分析了Lugre 動摩擦模型對系統動力學行為的影響，為該類系統的參數優化及穩定性分析提供一定的理論依據。

(1)當激振頻率較小時，系統的分岔現象較為明顯，存在較多的運動周期，系統的動力學行為變得較為復雜，隨著激振頻率的遞增，系統的運動周期現象逐漸減小，直至進入穩定的周期1運動狀態。

(2)當激振頻率與間隙均較小時，系統的動力學行為較為復雜，總在混沌運動狀態和逆周期倍化分岔狀態之間變化，存在多周期運動狀態，運動過程較為復雜。但若將間隙控制在一定的范圍內時，隨著激振頻率的增加，系統的運動周期會越來越小，動力學行為也變得不再復雜。

圖4 系統運動相圖和時間歷程圖

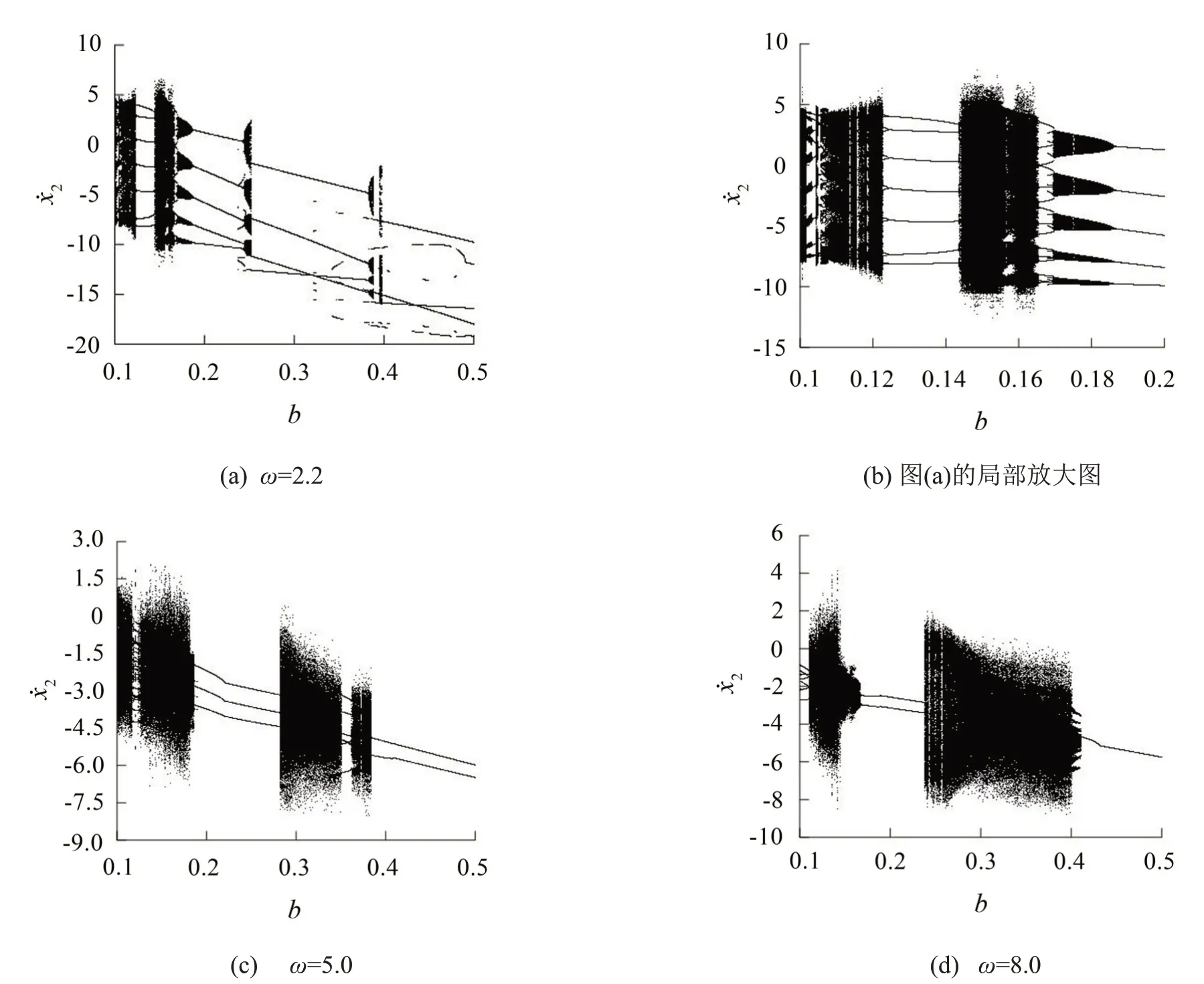
圖5 系統隨間隙變化的分岔圖