高壓油管壓力控制分析與研究
——以2019年全國大學生數學建模競賽A題為背景
(南通大學,南通 226000)
0 引 言
根據燃油壓力的變化量與密度變化量成正比的關系可知,當容積為定值的高壓油管內燃油的質量改變時,高壓油管內的壓力就會發生改變,如果保持高壓油管內的燃油質量不變,那么高壓油管內的壓力就會保持穩定的狀態,因此根據進出高壓油管的燃油質量守恒就能夠求解出單向閥每次開啟的時長。而當需要在一定的時間內將高壓油管內的壓力增加到150 MPa時,高壓油管內燃油的密度為變值,進入高壓油管的質量和噴出高壓油管的質量也在時刻改變。所以采用微元法分析每個時刻的質量的變化,然后通過積分的方法計算調整時長內進油質量和噴油質量的累加值。根據調整時長內進油量的累加值與噴油量累加值和高壓油管增加的油量之和相等求出單向閥開啟的時間。
1 模型的建立與求解
1.1 高壓油管穩壓時單向閥開啟時長的確定
高壓油管的示意圖如下,其中A點為燃油進入高壓油管的入口,B點為噴射器的噴油口。
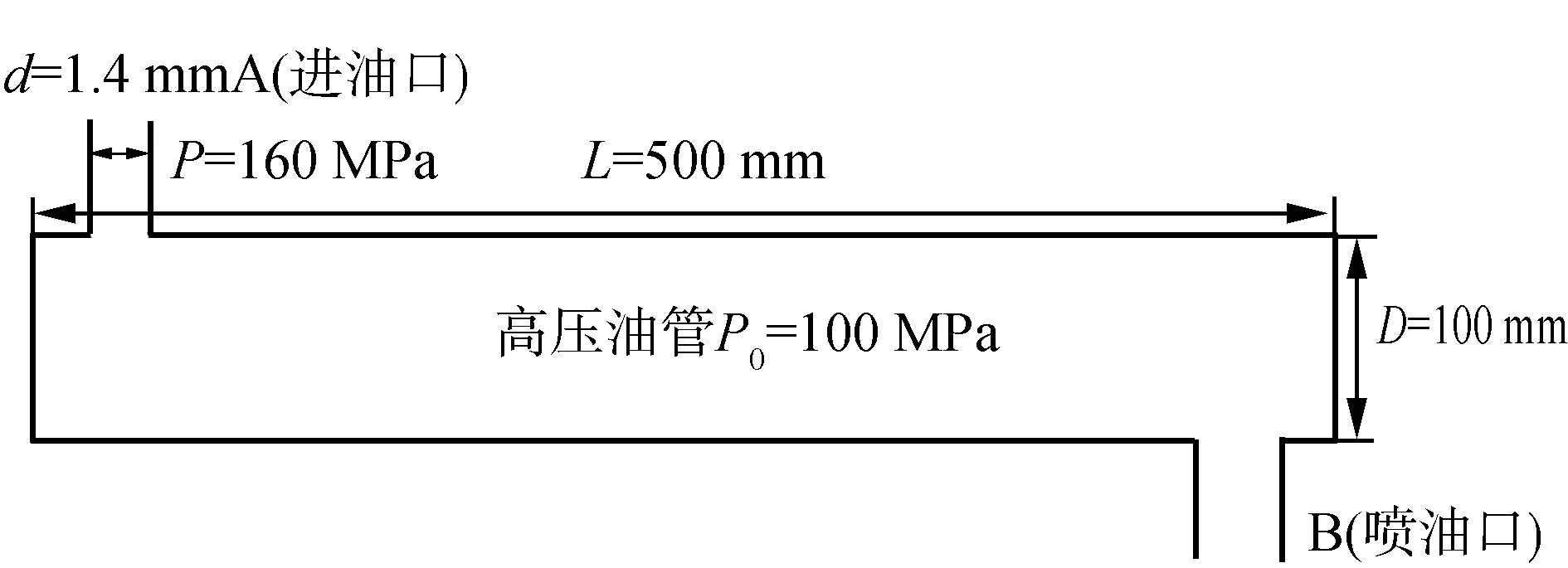
圖1 高壓油管示意圖
為了使高壓油管內的壓力穩定在100 MPa,根據質量守恒定律,單位時間的進油量和噴油量應該相等。假設1 s內進入高壓油管的燃油質量為MA,噴油器噴出的燃油質量為MB,則根據質量守恒定律建立單位時間長度為1 s時高壓油管進油質量和噴油質量相等的模型:
MA=MB
(1)
由于問題一已知噴油嘴每次工作時噴油速率v(mm3/ms)和噴油時間t(ms)的關系以及噴油嘴每秒工作次數k,且已知當壓力為100 MPa時燃油的密度,所以可以計算出壓力為100 MPa時每秒噴出燃油質量;根據提供的燃油進出高壓油管的流量公式,以及壓力變化量與密度變化量的關系求解單向閥開啟時每1 ms進入油管的燃油質量,從而可知1 s時間內單向閥開啟的總時間,進而可得單向閥每次開啟的時長,具體的計算過程如下:
(a)噴油質量的計算
噴油嘴在噴油的瞬間可認為燃油的密度等于高壓油管內的密度,則根據燃油質量的計算公式可得1 s內的噴油量為:
MB=kρ0VB
(2)
其中,ρ0表示當壓力為100 MPa時燃油的密度,即ρ0=0.850 mg/mm3;VB表示噴油嘴每工作一次所噴出的油量容積;k表示1 s內噴油嘴工作次數,即k=10。
根據已知噴油器的噴嘴口從B處噴油的速率v(mm3/ms)與時間t(ms)的關系如下:
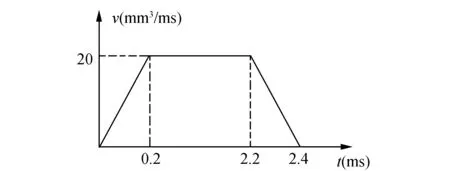
圖2 噴油速率示意圖
根據噴油嘴噴油速率示意圖可求出一次工作時間內的噴油體積為:
再根據公式得到1 s內高壓油管噴出的燃油質量:
MB=kρ0VB=10×0.85×44=374 mg
即單位時間(1 s)內高壓油管噴出的燃油質量為374 mg。
(b)進油流量的計算
已知進出高壓油管的流量計算公式為:
(3)
其中,Q表示單位時間流過小孔的燃油量(mm3/ms),C=0.85為流量系數;A為燃油進入高壓油管的小孔橫截面積(mm3);ΔP為進出油兩邊的壓力差;ρA為高壓側燃油的密度(mg/mm3),則可以得到單向閥開啟時每ms進入高壓油管的燃油流量為:
(3)
其中,PA=160 MPa為高壓油泵提供的壓力,P0=100 MPa為高壓油管內的初始壓力。
為了求解Q,則需計算進油量的橫截面積和高壓側燃油的密度,由于進油口處的小孔橫截面為圓形,則根據圓的計算面積可得:
(4)
其中,d為小孔的直徑,d=1.4 mm。
由于燃油從高壓油泵進入高壓油管時壓力發生了變化,所以高壓側燃油的密度不等于高壓油管內的密度,需根據燃料壓力差關于密度差的計算公式進行求解,公式如下:
(5)
已知彈性模量和壓力之間存在一定的對應關系,可記為E(P),對附件3的數據進行擬合則可得到任意一個壓力對應的彈性模量為E,以壓力P為自變量、E(P)為因變量進行擬合。擬合得到E(P)關于P的函數關系式為:
E(P)=1.003 8×10-4P3+1.082 5×10-3P2+
5.474 4P+1.531 9×103
(6)
則對公式(5)進行推導,得到任意壓力下燃油的密度ρ,推導過程如下:
(7)
則可得高壓側的燃油密度:
由于附件3給出了當壓力為160 MPa時,E=2 786.4 MPa,那么可以直接計算得到高壓側的燃油密度為0.868 7 mg/mm3,則單向閥開啟時每ms進油流量Q為:
(c)單向閥開啟時長
假設單向閥每次開啟的時長為t0(單位為ms),1 s內開啟的總時長為t,則根據每s內流進高壓油管內的燃油質量和噴出高壓油管的燃油質量相等,可得每1 s內單向閥開啟的總時長t為:
由于單向閥每工作一次都需要關閉10 ms,即兩次工作之間的間隔時間為10 ms,則可通過單向閥關閉的時長求出1 s內單向閥工作的次數n為:

從而根據總工作時長和工作次數的比值得到每次單向閥開啟的時長為:
1.2 單向閥開啟時長的調整
通過調整單向閥開啟的時長,在分別經過2、5和10 s的時間長度后使得高壓油管內的壓力從100 MPa增大到150 MPa,并在調整過程后使高壓油管的壓力穩定在150 MPa。對于容積一定的高壓油管,管內燃油質量的增加會導致壓力的增大,當高壓油管內的壓力增大50 MPa時,高壓油管中需要增加一定的燃油質量。由于在調整時長內,燃油的密度為變值,進入高壓油管的質量和噴出高壓油管的質量也時刻在改變。因此采用微元法分析每個時刻的質量的變化,然后通過積分的方法計算調整時長內進油質量和噴油質量的累加值。
(a)調整時間內高壓油管內增加的燃油質量
當經過一定的調整時間后,高壓油管內的壓力穩定在150 MPa,則此時燃油的密度可由壓力變化量和密度變化量之間的關系求出,由(7)可得:
其中,P′=150 MPa,ρ′表示燃油在150 MPa壓力下的密度,計算可得ρ′=0.853 2 mg/mm3。則高壓油管內的壓力增大50 MPa時,高壓油管中需要增加的燃油質量為:
ΔM=M2-M1=ρ′V-ρ0V
(8)
其中,V表示高壓油管的容積,其計算公式為:
(9)
其中,D為高壓油管的內直徑;L表示高壓油管的內腔長度,聯立公式(8)和(9)求得ΔM=125.756 mg。
(b)進油質量和噴油質量積分公式的推導。假設在調控時間內某個時刻高壓油管內的壓力為PB,進油時燃油進入高壓油管的質量為dMA,則對任意時刻的進油質量計算公式為:
dMA=QAρAdt
(10)
其中,ρA=0.868 7 mg/mm3;QA表示進油口的流速,根據進出高壓油管油量的流量公式(3)可知:
(11)
將公式(11)代入公式(10)可得:
(12)
假設當壓力為PB時燃油的密度為ρB,根據公式(5)和公式(6)可得任意時刻壓力PB和初始壓力的關系:
(13)
其中,E(ρB)表示燃油密度為ρB時的彈性模量,將公式(13)代入(12)則可得:
(14)
對該公式進行積分得到調整時間內進油質量的累加值MA為:
(15)
其中,Pi、ρBi分別表示調整時間內任意時刻i高壓油管內的壓力和密度;E(PBi表示壓力為Pi時的彈性模量。假設任意時刻噴油質量為dMB,同理可得噴油口在調整時間內累加噴出的燃油質量的積分公式推導如下:
根據圖1可知噴油口在2.4 ms內的噴油速率與時間的關系為:
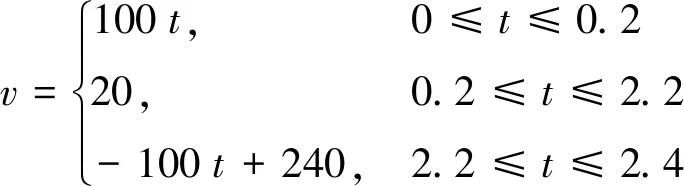
(16)
所以可知噴油時噴油速率是關于時間t的分段函數,可記為v(t),那么:
dMB=v(t)ρBdt
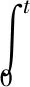
(17)
(c)求解單向閥的開啟時長
根據質量守恒定律可知在調整時間內壓力增加50 MPa時,進油的質量需滿足出油質量和高壓油管增加質量之和,即:
MA=MB+ΔM
(18)
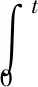
采用變步長搜索算法對積分公式進行求解,具體的算法步驟如下:
Step 1.定義變量p1,ρ1,ma,mb,i,M,分別表示高壓油管內的燃油的壓強、密度、進油總質量、出油總質量、A處單次開啟時長和高壓油管內燃油總質量,并給p1賦初值100 MPa,給ρ1賦初值0.850 mg/mm2,給ma和mb賦初值為0,給M1賦初值為33 379.4 mm3,給i賦初值為0.1 ms,以0.1 ms為步長,1 ms為終點遍歷每一個i進行搜索。
Step 2.將調整時間2 s離散化為2 000個等長時間段,定義變量j表示離散化的調整時間,j的范圍為[1,2 000]。
Step 3.利用公式(3)、公式(5)計算p1,ρ1,ma,mb,進行迭代搜索,記錄到每一個離散化時間的進油質量和出油質量,并計算高壓油管內燃油總質量M1。
Step 4.若高壓油管內燃油總質量M1大于等于高壓油管內壓強為150 MPa時高壓油管內燃油總質量或j達到2 000,記錄此時高壓油管內燃油總質量M1與壓強為150 MPa時高壓油管內燃油總質量的誤差,結束遍歷,否則轉Step 3。
Step 5.求出誤差的絕對值最小的i,以0.01為步長對[i-0.1,i+0.1]范圍內的每一個值進行搜索,記錄誤差絕對值最小的i即為開啟時長的優解。
根據上述算法求解得到:
當調整時間為2 s時,單向閥每次開啟時長需為0.87 ms;當調整時間為5 s時,單向閥每次開啟時長應為0.76 ms;當調整時間為10 s時,每次開啟時長為0.75 ms。
2 結束語
文中根據質量守恒定律,建立單位時間內(ms)進出高壓油管燃油質量守恒模型,計算出單向閥單次開啟時長。在質量守恒模型基礎上,利用變步長搜索法分別計算出經過2、5和10 s的時間長度后使得高壓油管內的壓力從100 MPa增大到150 MPa,并穩定在150 MPa時單向閥單次開啟時長。該模型還可以推廣用于解決其他工程管道的控制和決策問題。

