考慮初始損傷效應的重力壩動力體系可靠性研究

梁禮繪

(中國電建集團昆明勘測設計研究院有限公司，云南 昆明 650051)

混凝土壩在全生命周期中結構和材料性能都是隨工作狀態和環境不斷變化的。主要表現為兩個方面：一是混凝土本身由于材料特性等因素，不可避免地會有初始缺陷[1]存在(如空隙、微裂縫等)；二是巖石中節理裂隙等對巖石的變形和破壞特征產生不確定性影響[2]。特別是地震條件下，初始損傷狀態使得結構對動荷載敏感性增強。當前時段重力壩系統損傷狀態及其效應的影響不容忽視。因此，在評估壩體壩基系統抗震可靠性時，應當在結構系統的功能函數中考慮初始損傷狀態的描述。

對于材料損傷描述而言：一種是通過唯象學模型以內變量的方法從宏觀上處理損傷問題，借助有效應力的概念，將損傷狀態以內變量形式引入到損傷狀態方程；另一類方法是考慮微裂縫形成的物理機理，從微觀力學角度導出材料的損傷方程。封伯昊等[3]利用損傷邊界面的概念考慮結構損傷，引入可靠性分析中，進而分析結構安全性。目前，這一交叉領域的研究還處于探索階段，對于考慮材料初始損傷狀態的動力條件下壩體壩基體系抗震可靠性的研究還較少涉及。

本文研究對象是混凝土重力壩。通過引入損傷邊界面和有效材料狀態參量，分別考慮壩體混凝土和壩基巖體初始損傷效應，分別構造了包含損傷狀態的重力壩混凝土和巖基的強度極限狀態方程，在此基礎上建立了重力壩體系抗震可靠度的分析模式。通過該分析模式，對某混凝土重力壩工程實例在初始損傷狀態下的可靠性進行了分析研究。

1 考慮損傷效應的系統功能函數的建立

1.1 材料損傷狀態及其效應的引入

混凝土材料初始損傷狀態采用損傷邊界面進行考慮。損傷邊界面，是Fardis[4]研究混凝土損傷時提出的包絡面，這一概念包含的應力空間可以用于描述混凝土在單調和循環加載下的損傷。采用Hsieh-Ting-Chen[5]提出的強調大主應力貢獻四參數破壞面模型描述混凝土的破壞行為，同時考慮初始累積損傷量D0，取值區間[7]為[0，0.7]。對于本文算例：按照以彈性模量表征的損傷變量的定義，對于剛建成的壩體結構，混凝土的初始損傷為0.05左右，因此，在靜力分析時取D0=0.05；動力分析中，根據文獻[3]對水工混凝土進行的試驗，應變在D0=0.3左右出現拐點，因此，取D0=0.3。本文暫不考慮動力荷載作用過程中的損傷演化情況。

其次，對于壩基巖體，引入有效材料狀態參量來表征計算時段前的初始損傷狀態。

損傷會使材料微觀結構發生變化，從而進入新的材料狀態[11]，造成材料特性隨損傷而變化，發生變化的材料特性參數被稱為有效材料狀態參量[12]，例如巖石的有效彈性模量和有效破壞強度。文獻[13]指出，損傷后的巖石材料強度就會隨其損傷狀態和應力狀態而變化。根據文獻[2]的研究，通過巖石樣品裂紋產狀的統計觀測信息，發現巖石的損傷變量為滿足[0，1]區間內的β分布。

1.2 功能函數模型的建立

混凝土材料破壞以受拉破壞為主，重點只考慮混凝土的受拉破壞[14]。對于重力壩結構，本文采用如下復合強度準則：壩體采用考慮損傷邊界面的混凝土Hsiegh-Ting-Chen四參數破壞準則；基巖采用考慮材料等效損傷狀態的Drucker-Prager準則。

將混凝土損傷邊界面模型代入其破壞準則中，經變換，對應于初始損傷邊界面的混凝土強度極限狀態方程為：

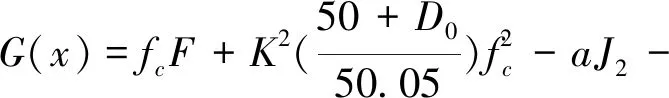
(1)

式中，F—主應力狀態函數，根據不同的拉壓組合有不同的形式。G(x)>0—可靠狀態。

對應于考慮損傷效應DP準則的基巖材料的強度極限狀態方程為

(2)

式中，各符號的含義如前所述，G(x)<0為可靠狀態。

2 重力壩損傷體系抗震可靠度計算方法

本文研究的重力壩擋水壩段，其功能目標確定為對應于承載能力極限狀態的強度安全和抗滑穩定安全，由于穩定問題歸根結底是強度問題，因此重力壩整體可靠性歸結為壩體和混凝土強度失效路徑的體系可靠性。綜上，重力壩體系抗震可靠度求解方法的思路為：首先，求解特定地震條件下的特定失效路徑的失效概率；然后，考慮重力壩體系不同失效路徑的相關性，求解其在特定地震條件下的體系可靠度；最后，考慮地震作用的隨機性，基于全概率公式可以得到動力條件下的總失效概率及其可靠指標。

2.1 失效路徑功能函數擬合及其失效概率

地震作用下重力壩的響應及失效函數與材料、荷載參數的關系十分復雜，且各變量之間多為非線性的隱式函數關系，如式(1)—(2)。因此，本文采用響應面擬合方法來模擬復雜的隱式函數。

在某特定地震動峰值加速度作用下，基于ANSYS中的可靠度PDS平臺，借助APDL語言計入輸入變量統計特性，首先采用振型分解反應譜法進行大壩系統動力條件下的隨機有限元計算，得到重力壩系統應力場統計特性，進而采用響應面函數將式(1)—(2)統一表達為：

(3)

式中，n—隨機變量的個數，a、bi、ci為待定參數。

這樣，結構響應量的統計特性也被計入。根據C.G.Bucher和U.Bourgund[15]建議的方法，采用內插技術來確定待定因子。

最后，采用基于該響應面擬合方程，求得特定失效路徑的失效概率，進而按照式(4)求解某個特定地震動條件下大壩系統的體系可靠度。

maxPfi≤Pf≤∑Pfi

(4)

式中，maxPfi—各失效路徑完全相關的情況；∑Pfi—各失效路徑相互獨立的情況。

2.2 考慮地震隨機性的全概率動力可靠度

特定地震動峰值下重力壩體系的失效概率，可以記為不同水平地震加速度系數條件下的失效概率，較難用精確的解析式表達，因此，通常采用數值擬合積法和全概率公式計算[16]得到總失效概率及其可靠指標。

(5)

β=Φ-1(1-Pf)

(6)

式中，f(A)—水平地震加速度系數的概率密度函數f(A)=Bbe-bA，A≥0，根據現有統計資料，暫取B=0.0499，b=19.948；Φ(?)—標準正態分布函數。水平向運動峰值加速度A與水平地震系數KH之間存在關系KH=A/g，其中g為重力加速度。

3 工程算例

某碾壓混凝土重力壩，壩高149m。場地類別為一類場地。設防烈度100年超越概率2%水平峰值加速度為0.284g。豎向加速度代表值取水平向ah的2/3。在動力計算中取無質量地基，動水壓按照Westergaard公式計算。考慮材料參數隨機性，本文不考慮變異系數小于0.05的變量的隨機性，將其視為確定性變量，同時離散化處理地震隨機變量。各參數取值見表1，限于篇幅，只列出變異系數較大的變量。對于初始損傷狀態，混凝土動力初始累積損傷量取為0.3，巖基的初始損傷由初始孔隙率折算[12]為0.09。

表1 隨機變量統計特征值

3.1 失效路徑的確定

參照文獻[18]的研究，本文考慮地基中2條失效路徑、壩體中3條失效路徑，以及壩體地基間的一條交叉失效路徑，共6種失效路徑。對于前四條路徑，將壩踵處壩體地基單元中可靠性指標最小的單元作為初始失效單元，采用逐步“殺死單元”的方法，搜尋下一個可能失效單元，進而找到可能出現的失效路徑，直到失效路徑上的累積失效概率不大于1.00%時，搜尋結束，并認為該路徑已達到穩定[19]。

3.2 重力壩體系抗震可靠度

首先分析不同水平地震系數下各典型失效路徑的失效概率。

基于響應面法的思想，將不同路徑上單元強度的極限狀態功能函數作為隨機輸出變量，采用ANSYS PDS模塊進行隨機有限元分析，分別擬合了失效單元強度的極限狀態功能函數，并計算相應的失效概率和可靠度指標。

同時，重力壩體系可靠度屬于串聯體系可靠度問題，按照式(4)考慮各條失效路徑之間的相關性，估算重力壩強度體系的可靠性及相應的失效概率的上下界限。進而得到不同水平地震系數下各典型失效路徑及體系的失效概率，如圖1所示。

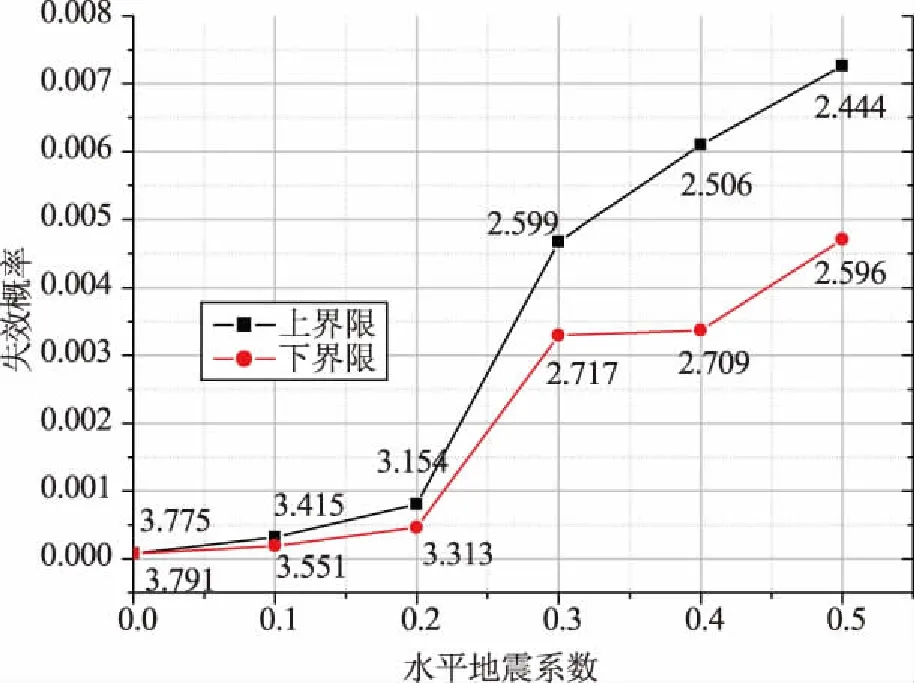
圖1 不同水平地震系數下體系的失效概率

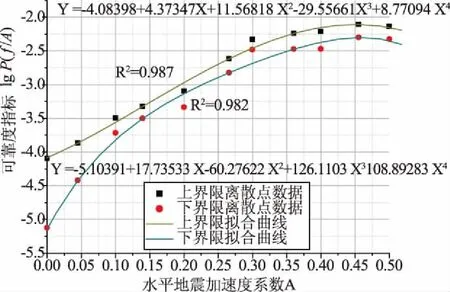
圖2 不同水平地震系數與失效概率對數值的擬合曲線

由圖1可知，不同路徑的強度可靠指標隨著水平地震系數的增大而減小；隨著地震加速度的增大，壩體體系可靠度不再由建基面失效路徑決定，而是由靠近壩頂的下游折坡處所在層面的失效路徑決定，也體現了地震效應對壩體上部影響顯著。本文以對數形式進行描述。對水平地震系數與失效概率上、下界限值的關系進行曲線擬合，得到的擬合函數，如圖2所示，方程為：

(7)

式中，上界限擬合函數的參數為C=-4.08398，B1=4.3735，B2=11.5682，B3=-29.5566，B4=8.7709；下界限擬合函數的參數為C′=-5.1039，B′1=17.7353，B′2=-60.2762，B′3=126.1103，B′4=-108.8928。經檢驗，擬合函數在A=0～0.5的區間內擬合優度均接近于1。

將式(7)代入式(5)并進行A=0.5的右截尾計算，得到重力壩體系在地震作用下的失效概率為Pf=4.63011×10-6～1.0305×10-5，相應的可靠指標為4.258～4.433。

3.3 計入損傷與不計入損傷的對比

針對水平地震系數為0.2的情況，分別對大壩計入初始損傷和未計入初始損傷狀態下的典型路徑上單元強度可靠性進行分析，結果如圖3—4所示。從圖3—4可以看出：

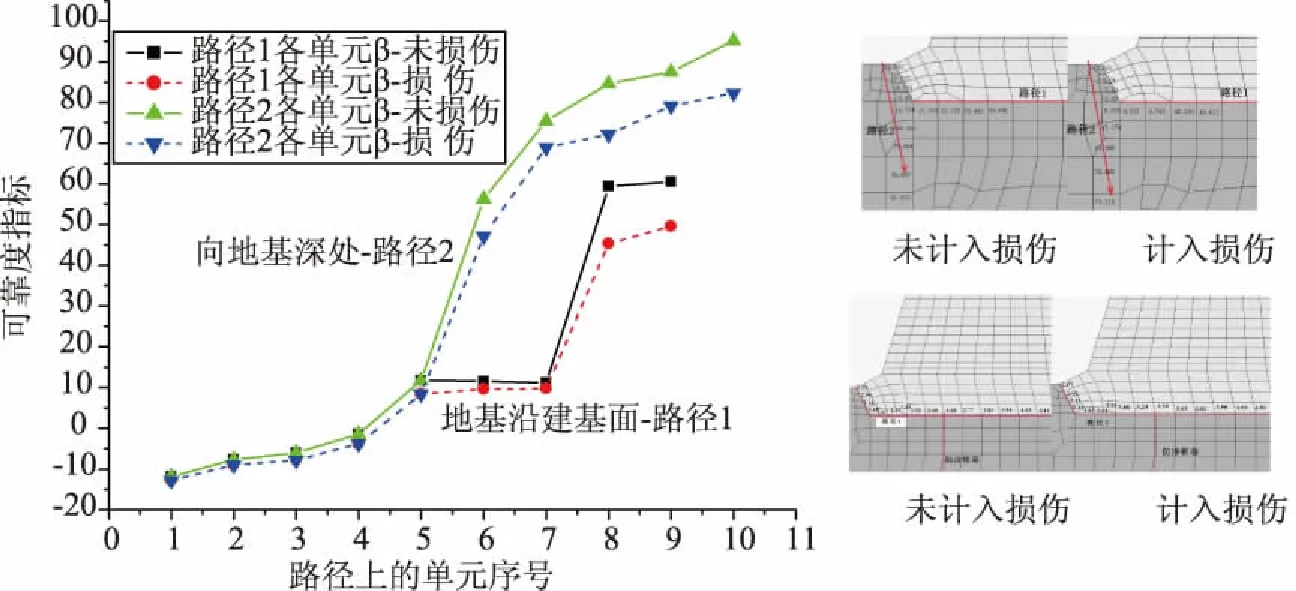
圖3 不同初始狀態下壩基失效路徑單元強度可靠度

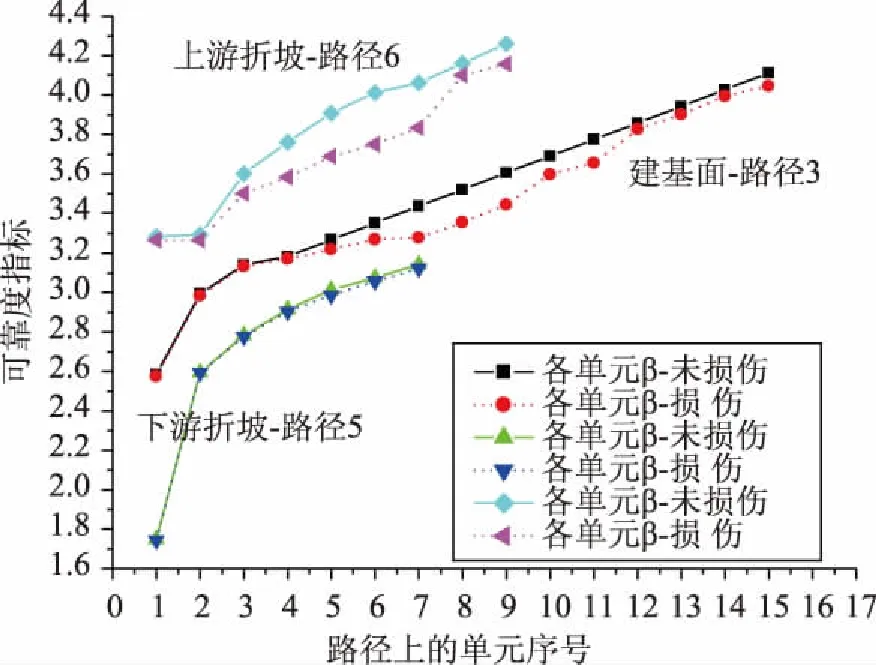
圖4 不同初始狀態下壩體失效路徑單元強度可靠度

(1)兩種不同的初始狀態下，壩體可靠度與壩體應力的分布規律基本一致，混凝土壩體可靠度最低的區域均位于壩踵和下游折坡點單元；壩踵單元的可靠指標分別為β損傷=2.57、β非損傷=2.58；下游折坡點單元的可靠指標分別為β損傷=3.267、β非損傷=3.283。

(2)從數值上看，隨著路徑向壩體內部發展，單元的強度可靠性不斷增大。壩踵區域，基巖材料單元強度失效概率遠大于壩踵混凝土。即該條件下，壩踵區域的破壞首先出現在基巖內部并向地基深處發展。

(3)從壩體內部幾條失效路徑的單元失效概率來看，動力條件下，下游折坡處單元強度最先失效。

4 結論

本文通過引入損傷邊界面和有效材料狀態參量，分別構造了包含初始損傷狀態內變量的重力壩混凝土和巖基的強度極限狀態方程，并在此基礎上建立了重力壩體系抗震可靠度的分析模式。實例分析表明，該分析模式使得在重力壩運行的特定時段的體系可靠性分析和評價更為合理，并能對混凝土重力壩在運行期內基于損傷演化特征的時變可靠度進行初步預測。主要得出了以下結論。

(1)以損傷內變量的形式，提出了考慮損傷狀態耦合影響的混凝土四參數強度準則和巖體修正DP破壞準則，建立了混凝土和巖石材料含初始損傷效應的極限狀態功能函數模型，并在此基礎上建立了重力壩體系抗震可靠度分析模式。

(2)兩種不同的初始狀態下，壩體可靠度與壩體應力的分布規律基本一致。混凝土壩體可靠度最低的區域均位于壩踵和下游折坡點，在壩踵和壩踵與基巖的結合部損傷最顯著，損傷區域從壩體與基巖結合部向壩體和基巖內部逐步擴展，并逐步向內減弱，同時，在壩趾處也發生一定程度的損傷。對于壩體區域，在動力條件下，下游折坡處單元強度最先失效。

(3)計入初始損傷后，重力壩在壩體地基交接處點可靠度下降較大；敏感性分析表明，在動力條件下，基巖彈模與地基單元強度失效負相關；壩體混凝土單元強度可靠性與基巖彈模負相關，與混凝土抗壓強度正相關，且顯著敏感性達到10%。即從可靠度的角度說明了壩頭部位置換高標號混凝土有利于提高壩體抗震性能。