基于粒子群優化LSTM 的股票預測模型

宋剛，張云峰，*，包芳勛，秦超

（1.山東財經大學 計算機科學與技術學院，濟南250014； 2.山東財經大學 山東省數字媒體技術重點實驗室，濟南250014；3.山東大學 數學學院，濟南250100）

股票市場行情預測一直是投資者迫切關注的話題，然而股票數據具有高噪聲、動態、非線性和非參數等特點［1］，準確地預測股票價格仍是一項具有挑戰性的工作。隨著人工智能技術的發展，深度學習以其在機器翻譯［2］、語音情感識別［3］、圖像識別［4］等方面的優異表現受到廣泛關注。與傳統統計模型相比，深度神經網絡（DNN）可以通過分層特征表示來分析深層和復雜的非線性關系，適合處理股票數據分析這種多因素影響、不穩定、復雜的非線性問題。

循環神經網絡（Recurrent Neural Network，RNN）將時序的概念引入到網絡結構設計中，使其在時序數據分析中表現出更強的適應性。Hochreiter和Schmidhuber通過對RNN網絡單元結構進行改進提出了長短期記憶（Long Short-Term Memory，LSTM）模型［5］，通過設計控制門結構彌補了RNN的梯度消失和梯度爆炸、長期記憶能力不足等問題，使得RNN能夠真正有效地利用長距離的時序信息［6］。目前，LSTM 神經網絡已經成功應用于語音識別［7-8］、文本處理［8］等方面，基于LSTM神經網絡在這些方面的優異表現，應用其對金融時間序列進行研究受到廣泛關注。2015年，Chen等［9］使用LSTM模型預測了中國股票市場的股票價格；2016年，Jia［10］驗證了LSTM模型預測股票價格趨勢的有效性；2017年，Nelson等［11］基于股票歷史數據和技術指標使用LSTM模型預測了未來股票市場趨勢，并與其他機器學習方法進行比較，該實驗表明LSTM 預測模型具有更高的預測精度；2018年，Fischer和Krauss［12］應用LSTM模型對標準普爾500指數波動情況進行預測，與隨機森林（RAF）、DNN和邏輯回歸分類器（LOG）相比LSTM模型具有較好的預測效果。

與其他神經網絡模型類似，LSTM 神經網絡模型中部分參數需要人為設置，如時間窗口大小、批處理數量、隱藏層單元數目等。這些參數直接控制網絡模型拓撲結構，不同參數訓練出模型的預測性能差異巨大，因此選擇合適的模型參數就顯得尤為重要。目前，對于網絡模型超參數的選擇往往依賴研究者的經驗和多次實驗結果，耗費大量的人力和計算資源。因此，本文提出一種基于自適應粒子群優化（PSO）的LSTM 股票價格預測模型（PSO-LSTM），利用自適應學習策略的PSO算法對股票數據特征與LSTM神經網絡拓撲結構進行匹配，獲得更高的預測性能。在此基礎上，本文選取滬市浦發銀行、深市五糧液、港股恒隆集團股票數據，構建PSO-LSTM 模型對第2日股票收盤價進行預測。

1 相關工作

1.1 LSTM 神經網絡

LSTM是一種特殊的循環神經網絡。它通過精心設計“門”結構，避免了傳統循環神經網絡產生的梯度消失與梯度爆炸問題，能有效地學習到長期依賴關系。因此，在處理時間序列的預測和分類問題中，具有記憶功能的LSTM 模型表現出較強的優勢。

如圖1所示，LSTM 是由多個同構單元格組成，該結構能夠通過更新內部狀態來長時間存儲信息，A表示3個單元具有相同的單元結構。每個單元格由4個主要元素構成：輸入門、遺忘門、輸出門和單元狀態。

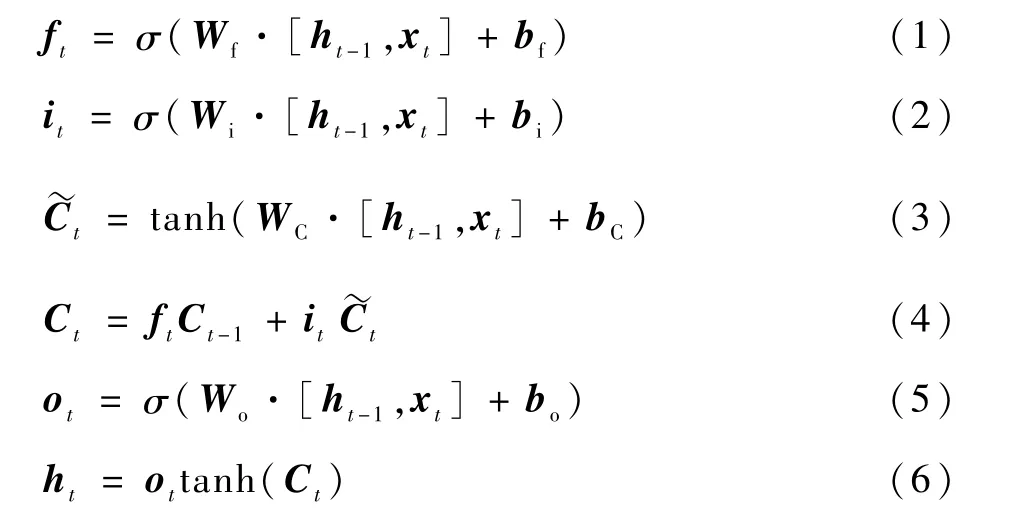
式中：x為LSTM單元的輸入向量；h為單元格輸出向量；f、i、o分別表示遺忘門、輸入門和輸出門；C表示單元狀態；下標t表示時刻；σ、tanh分別為sigmoid、tanh激活函數；W 和b分別表示權重和偏差矩陣。

LSTM的關鍵是單元狀態C，它在t時刻保持單元狀態的記憶，通過遺忘門ft和輸入門it進行調節。遺忘門的作用是讓細胞記住或忘記它之前的狀態Ct-1，輸入門的作用是允許或阻止傳入信號更新單元狀態。輸出門的作用是控制單元狀態C輸出和傳輸到下一個單元格。LSTM 單元的內部結構是由多個感知器構成的，反向傳播算法通常是最常見的訓練方法。

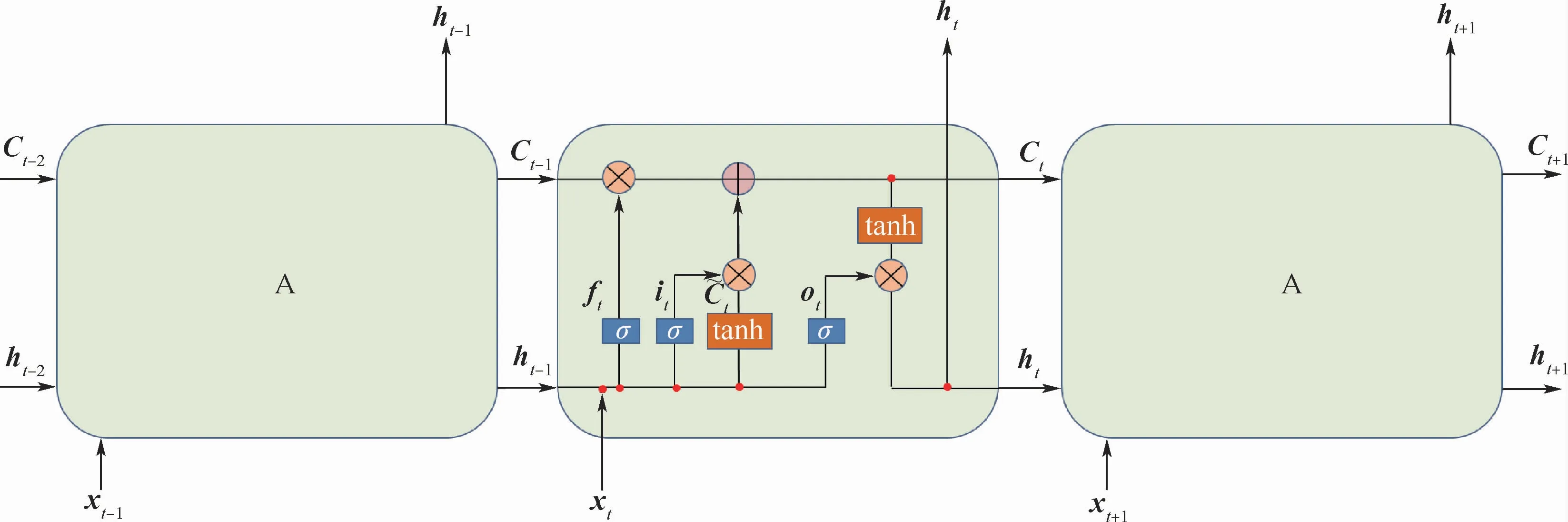
圖1 LSTM單元結構Fig.1 LSTM unit structure

1.2 傳統粒子群算法

粒子群算法的思想源于對鳥類社會行為的研究。鳥群捕食最簡單有效的方法是搜索距離食物最近的鳥的所在區域，通過個體間的協助和信息共享實現群體進化。算法將群體中的個體看作多維搜索空間中的一個粒子，每個粒子代表問題的一個可能解，其特征信息用位置、速度和適應度值3種指標描述，適應度值由適應度函數計算得到，適應度值的大小代表粒子的優劣。粒子以一定的速度“飛行”，根據自身及其他粒子的移動經驗，即自身和群體最優適應度值，改變移動的方向和距離。不斷迭代尋找較優區域，從而完成在全局搜索空間中的尋優過程。

傳統粒子群算法描述為：假設在一個D維搜索空間，m 個粒子構成的一個種群X=｛x1，x2，…，xm｝，其中xi=［xi1，xi2，…，xiD］，設t時刻xi的特征信息為

則該粒子在t+1時刻的速度和位置信息更新：

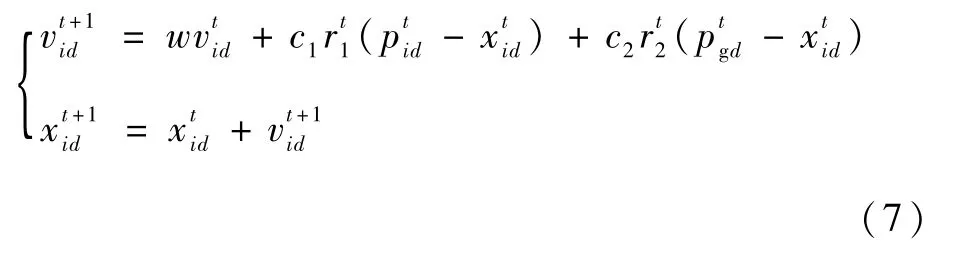
式中：w為慣性權重，控制粒子在全局探測和局部開采間的有效平衡；c1和c2為學習因子，分別調整飛向自身和全局最好位置方向的步長；r1和r2為均勻分布在［0，1］之間的隨機數。為避免粒子搜索，一般將其速度和位置分別限制在［-Vmax，Vmax］和［-Xmax，Xmax］之內。

2 自適應PSO 的LSTM 神經網絡預測模型

2.1 自適應學習策略的PSO算法

本文借助聚類思想，根據粒子自身的分布情況，將整個種群自適應地劃分成若干子群［13］。對于每個子群，采用不同的學習策略分布對不同類型的粒子進行更新，提高種群多樣性。

采用一種具有較高聚類性能的快速搜索聚類方法實現子群的劃分［14］。該方法能自動發現數據集樣本的類簇中心，同時能夠實現任意形狀數據集樣本的高效聚類。其基本原理是：類簇中心具備2個基本特征，被局部密度較低的點包圍，且與局部密度較高的點距離較大。

在一個D維搜索空間中，由h個粒子構成的一個種群S=｛xi｝，其中xi=［xi1，xi2，…，xiD］，對于第i個粒子的第d維給出2個變量，粒子的局部密度ρid與到更高局部密度粒子間距離δid，其定義為

式中：dij為xid和xjd之間歐氏距離；dc為截斷距離。

對于局部密度ρid最大的樣本，其δid=maxj（dij）。

由式（9）可知，若xid的密度是最大局部密度，則δid遠大于其最鄰近粒子的δ距離。因此，子群的中心往往是δ異常大的粒子，這些粒子的密度ρ也相對較高，即選擇ρ和δ都較大的粒子作為聚類中心。對于其他粒子的xjd，將其歸入密度比xjd大且距離xjd最近的樣本所在的子群。

基于子群劃分的結果，將每個子群中的粒子分為普通粒子和局部最優粒子兩類。對于普通粒子，其主要在子群中最優粒子的引導下拓展局部搜索能力，更新公式為

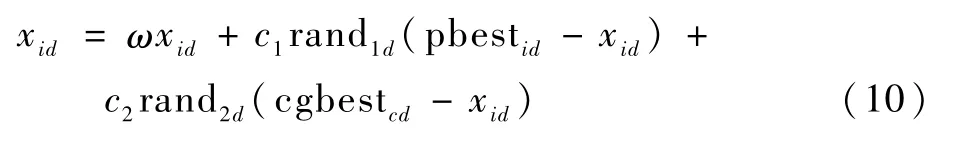
式中：ω為慣性權重；c1、c2為學習因子；rand1d、rand2d為區間［0，1］上的均勻分布隨機數；pbestid為第i個粒子第d維的最優位置信息；cgbestcd為第c個子群中的最優位置信息。

對于局部最優粒子，其主要通過綜合各子群的信息進行更新，以加強子群間的信息交互，更新公式為

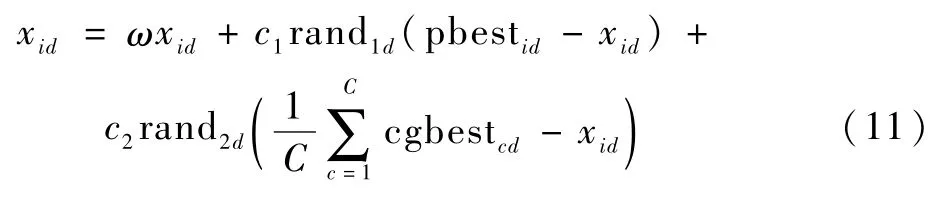
局部最優粒子一方面指導普通粒子的學習，另一方面作為子群間信息交互的媒介。在子群中，局部最優粒子引導著整個子群的搜索方向，若采用式（10）的學習策略，一旦局部最優粒子偏離最優解的搜索方向，會導致整個子群陷入局部最優。因此，局部最優粒子需要突破子群的控制，從其他子群中獲得信息。考慮到局部最優粒子是子群中最有可能找到最優解的粒子，式（11）利用各個子群中局部最優粒子的平均信息來指導粒子的更新。通過這種子群間信息的共享，促進子群間尋優信息的傳遞，進一步提高種群的多樣性，避免陷入局部最優。

2.2 PSO-LSTM 模型

股票數據作為一種金融時間序列，其受到多方面因素的影響，具有復雜的不穩定性、非線性與周期不確定性。為了準確地預測股票價格，本文以在時間序列分析中表現優異的LSTM模型為基礎，構建針對股票數據的預測模型。LSTM 模型中某些超參數的取值控制著模型網絡結構，為了使模型網絡結構與股票數據特征相匹配，本文將自適應PSO算法與LSTM 模型相融合，構建了PSO-LSTM預測模型。

PSO算法相較于其他生物智能演化算法的最大優勢在于算法設計簡單、收斂速度快，但易陷入局部最優。自適應PSO算法能夠根據種群自身的分布，通過自適應的子群劃分和粒子更新來避免局部最優，提高參數尋優的準確性。自適應PSO算法的自適應特性使得LSTM模型能夠根據股票數據的特征，快速、準確地確定最優超參數，實現LSTM模型網絡結構與股票數據特征的有效結合。

模型首先將時間窗口大小、批處理大小、隱藏層單元數目作為自適應PSO算法的優化對象，根據超參數取值范圍隨機初始化各粒子位置信息。通過式（8）、式（9）計算得到粒子的局部密度ρid及其到更高局部密度粒子的距離δid，實現自適應種群劃分。

其次，根據粒子位置對應的超參數取值建立LSTM 模型，利用訓練數據對模型進行訓練。將驗證數據代入訓練好的模型進行預測，以模型在驗證數據集上的平均絕對百分比誤差作為粒子適應度值。

適應度函數f定義為

根據各子群中粒子適應度值的取值情況，將粒子劃分為普通粒子、子群局部最優粒子與全局最優粒子。通過式（10）、式（11）分別對不同類別粒子位置信息進行更新。判斷是否達到終止條件，達到終止條件即得到優化目標的最優值；否則，重新根據粒子位置信息進行種群劃分，計算各粒子適應度值，更新各粒子位置信息，直到滿足終止條件。

最后，以超參數最優值構建LSTM模型，通過股票數據進行訓練和預測。PSO-LSTM 模型架構如圖2所示。

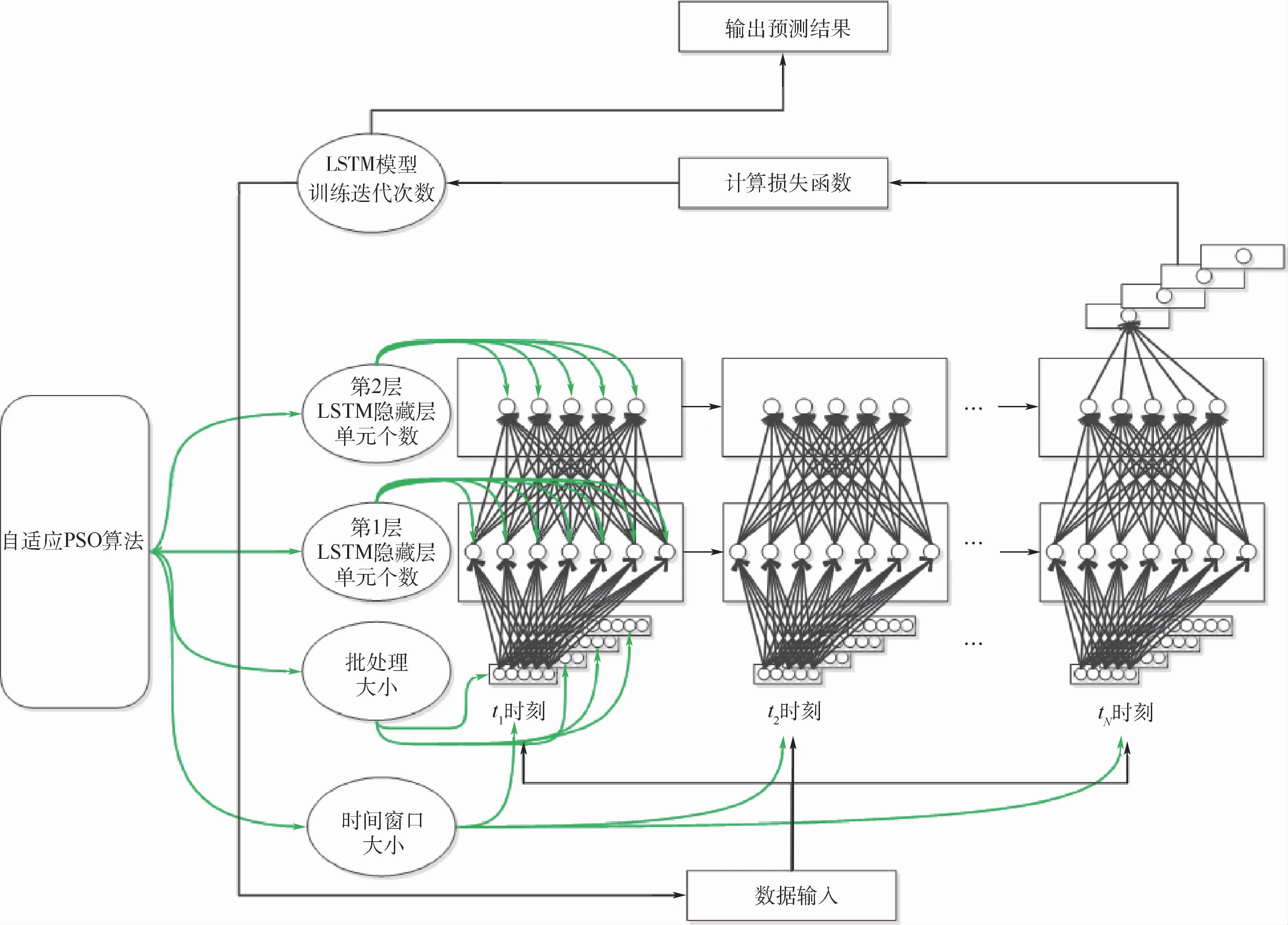
圖2 PSO-LSTM模型架構Fig.2 PSO-LSTM model architecture

2.3 算法流程

PSO-LSTM模型算法流程如下：

步驟1 將實驗數據分為訓練數據、驗證數據和測試數據。

步驟2 將LSTM模型中時間窗口大小、批處理大小、神經網絡隱藏層單元數目作為優化對象，初始化自適應PSO算法。

步驟3 根據式（8）、式（9）劃分子群。

步驟4 根據式（12）計算每個粒子的適應度值。以各粒子對應參數構建LSTM 模型，通過訓練數據進行訓練，驗證數據進行預測，將預測結果的平均絕對百分比誤差作為各粒子的適應度值。

步驟5 根據粒子適應度值與種群劃分結果，確定全局最優粒子位置pbest和局部最優粒子位置gbest。

步驟6 根據PSO算法的式（10）、式（11）分別對普通粒子和局部最優粒子位置進行更新。

步驟7 判斷終止條件。若滿足終止條件，返回最優超參數取值；否則，返回步驟3。

步驟8 利用最優超參數構建LSTM模型。

步驟9 模型通過訓練數據和驗證數據進行訓練，測試集進行預測，得到預測結果。

3 實驗與結果

實驗選取滬市A股（600000浦發銀行）、深市A股（000858五糧液）、港股（00010恒隆集團）為例進行研究，預測股票第2日收盤價格。股票歷史數據包含開盤價、收盤價、最高價、最低價、漲幅、振幅、成交量、成交額、換手率以及成交次數10個屬性。其中可能包含停盤停等操作所造成的數據空缺，對于空缺數據進行刪除操作，并按時間對數據進行排序。建立PSO-LSTM模型并與自回歸 移 動 平 均 模 型（ARIMA）［15］、支 持 向 量 機（SVM）［16］、多 層 感 知 機（MLP）［17］、RNN［18］和LSTM［19］模型進行對比實驗。

3.1 模型評價標準

本文選取均方根誤差（RMSE）、平均絕對百分比誤差（MAPE）、平均絕對誤差（MAE）、均方誤差（MSE）和決定系數R2作為評價指標對模型預測效果進行定量評價。其中RMSE、MAPE、MAE、MSE數值越小，模型預測結果與真實值偏差越小，結果越準確；決定系數R2越接近1，代表擬合優度越大，模型預測效果越好。具體公式定義為

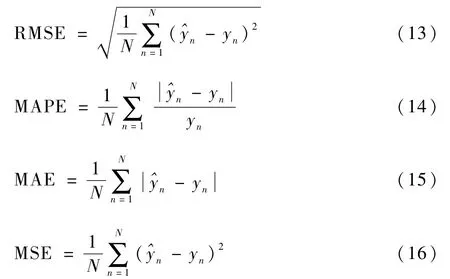
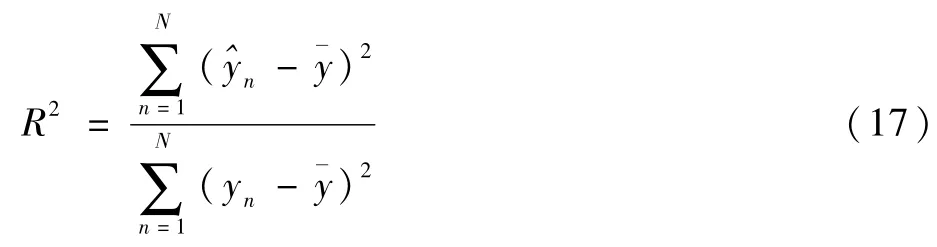
式中：N為實驗預測次數；^yn為模型預測值；yn為真實值；ˉy為真實值的平均值。

3.2 模型參數設置

PSO-LSTM 模型結構由輸入層、兩層LSTM層、輸出層組成，損失函數使用均方誤差，模型訓練過程采用Adam算法進行優化，網絡模型的搭建在Keras框架下實現。該模型將時間窗口大小、批處理大小、訓練次數和隱藏層單元個數設置為LSTM模型超參數。為了減少人為因素對模型的影響，實驗根據股票數據具體情況，對超參數的取值范圍設置如下：指定時間窗口大小取值范圍［1，20］，批處理大小取值范圍［1，60］，隱藏層單元個數取值范圍［10，30］。同時設置粒子群粒子個數為30，最大迭代次數為500，速度慣性權重ω為0.8，加速系數和為2。

PSO-LSTM訓練次數由模型誤差損失情況直接確定，模型迭代到800次時誤差損失函數達到收斂狀態。因此PSO-LSTM 模型的訓練次數為800。

3.3 實驗分析

3.3.1 滬市股票預測

浦發銀行2016-01-04—2018-12-21日K數據共計708條，其中70%作為訓練數據、20%作為驗證數、10%作為測試數據。自適應PSO模型的最優超參數為：時間窗口大小為10，批處理大小為58，第1層隱藏層單元個數為12，第2層隱藏層單元個數為22。實驗結果如圖3所示：綠色實線表示測試數據的股票收盤價真實值，紅色實線表示不同預測模型的股票收盤價預測值。預測結果顯示ARIMA模型預測值曲線在趨勢上非常符合股價真實值，然而在每個時間點處的預測值與真實值之間總保持一定誤差，具有明顯的滯后性。這是由于ARIMA模型采用了分步預測方法，每個時間點的預測值均為歷史時刻的真實值預測產生。因此ARIMA模型預測曲線總是落后于股價真實值曲線說明ARIMA模型的預測效果并不好，其預測精度可由模型評價指標進行比較；從其他模型預測結果來看，本文提出的PSO-LSTM 模型的預測曲線更接近股價真實值曲線，特別是在股價波動劇烈處的預測效果優于其他模型。

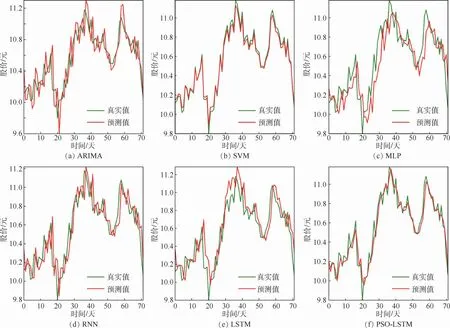
圖3 上海浦發銀行各模型預測結果比較Fig.3 Comparison of prediction results of various models for Shanghai Pudong Development Bank

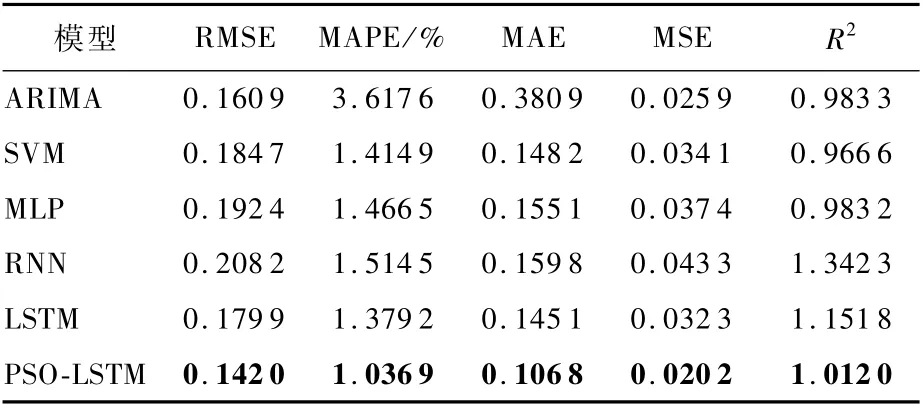
表1 上海浦發銀行各模型評價指標比較Table 1 Comparison of various models’evaluation indicators for Shanghai Pudong Development Bank

為進一步驗證該模型的預測性能，表1給出各預測模型的評價指標計算結果。PSO-LSTM模型預測誤差在RMSE、MAPE、MAE、MSE評價標準下都低于其他預測模型；在決定系數R2評價標準中，該模型計算結果比其他預測模型更接近1，表明PSO-LSTM模型的預測性能優于其他模型。特別地，PSO-LSTM模型MAPE指標比ARIMA模型低71%，比RNN模型低31%，模型預測精度顯著提高；PSO-LSTM 模型的各項指標優于LSTM 模型，但兩者差距并不明顯，主要原因是這兩種預測模型具有相同的單元結構；而PSO-LSTM 模型最突出的優勢在于構建過程中不需要人工調參，而且預測結果比普通LSTM模型更優。

為了進一步研究該模型與傳統LSTM 模型的有效性與穩定性，實驗將浦發銀行2018-12-24—2019-03-12日的日K數據平均分成5組，分別利用LSTM 模型和PSO-LSTM 模型進行預測，預測結果如圖4所示。圖中：綠色曲線表示股價真實值，藍色曲線表示LSTM模型預測值，紅色曲線表示PSO-LSTM模型預測值。從圖中可以看出，對于第2組、第3組和第5組數據，PSO-LSTM 模型的預測值曲線比LSTM模型更逼近股價真實值曲線。對于第1組和第4組數據，PSO-LSTM 模型與LSTM模型的預測結果非常接近。

表2給出兩種預測模型的RMSE指標比較結果。除了在第1組數據中LSTM 模型的RMSE指標具有微弱優勢，PSO-LSTM 模型在其他4組數據預測的RMSE指標都優于LSTM 模型。特別地，在第5組數據測試中PSO-LSTM 模型的預測精度比LSTM 模型高了25%。實驗結果表明，本文提出的PSO-LSTM模型對于不同時段的浦發銀行股票價格均有較好的預測能力，在模型預測精度與模型預測穩定性方面比LSTM 模型更具優勢。

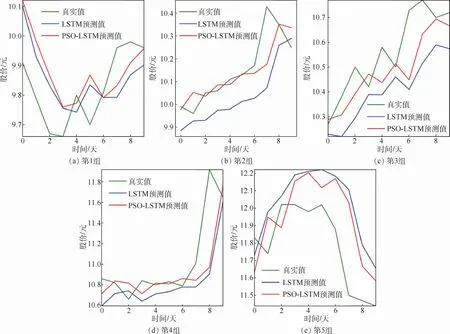
圖4 LSTM與PSO-LSTM預測結果比較Fig.4 Comparison of prediction results between LSTM and PSO-LSTM

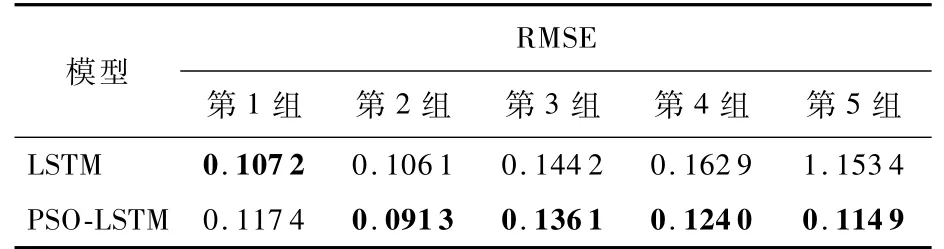
表2 LSTM 與PSO-LSTM 評價指標比較Table 2 Comparison of evaluation indicators between LSTM and PSO-LSTM

3.3.2 深市股票預測

五糧液2016-01-04—2018-12-21的日K數據共計726條，其中70%作為訓練數據、20%作為驗證數、10%作為測試數據。自適應PSO模型的最優超參數為：時間窗口大小為12，批處理大小為60，第1層隱藏層單元個數為16，第2層隱藏層單元個數為32。實驗結果如圖5所示。

如圖5所示，ARIMA模型在股票價格持續上漲或下跌時刻的預測效果較好，預測值接近股價真實值。但是在股價變化劇烈的時刻，ARIMA模型預測結果具有一定的延后性；SVM 模型在股價波動劇烈時刻的預測效果較差，預測曲線與真實值之間具有明顯的誤差；LSTM 模型的預測效果優于MLP模型與RNN模型；對于五糧液股票價格的預測，PSO-LSTM模型的預測效果最好，其預測值曲線能較好地逼近股價真實值。表3給出不同預測模型評價指標的比較結果，PSO-LSTM 模型除評價指標均優于其他預測模型。

3.3.3 港股股票預測

恒隆集團2016-01-04—2018-12-21的日K數據共計733條，其中70%作為訓練數據、20%作為驗證數、10%作為測試數據。自適應PSO模型的最優超參數為：時間窗口大小為10，批處理大小為48，第1層隱藏層單元個數為18，第2層隱藏層單元個數為24。實驗結果如圖6所示。ARIMA模型在股票價格漲跌拐點處的預測結果較差，對于股票上漲或下跌趨勢的預測有一定的滯后；SVM模型對于恒隆集團股票數據的預測表現最差，在某些時間點的預測結果與真實值之間具有明顯的差異。相較于其他模型，PSO-LSTM模型的預測效果仍表現較好。

表4給出不同預測模型評價指標的比較結果，PSO-LSTM 模型的各項評價指標均優于其他預測模型，其中R2指標非常接近1，這說明PSOLSTM模型對于恒隆集團股票數據的擬合最優度最佳。綜合滬市、深市、港股股票的預測結果表明，PSO-LSTM模型對于股票數據的預測具有較高的預測精度與穩定性。

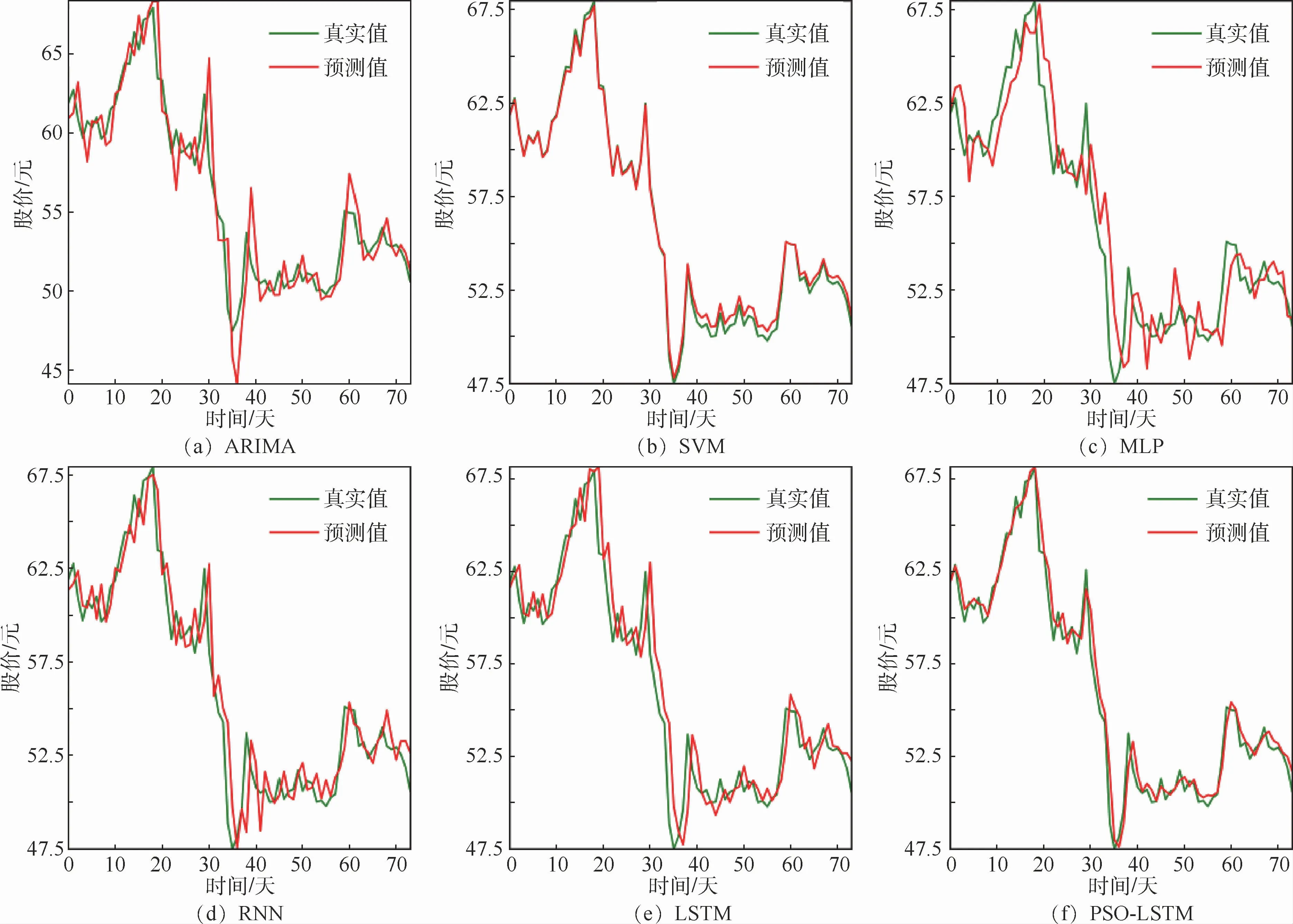
圖5 五糧液各模型預測結果比較Fig.5 Comparison of prediction results of various models for Wuliangye

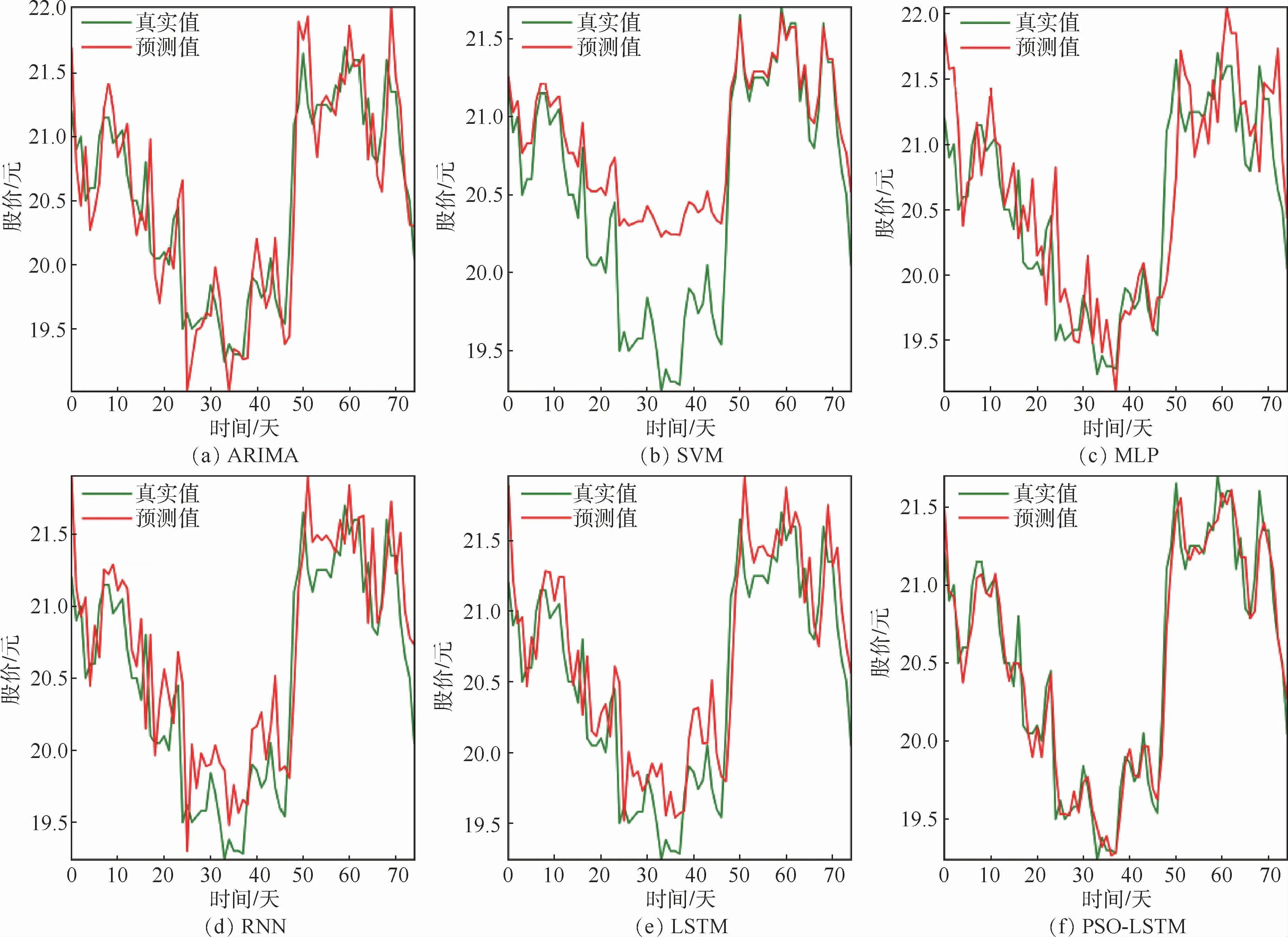
圖6 恒隆集團各模型預測結果比較Fig.6 Comparison of prediction results of various models for Hang Lung Group

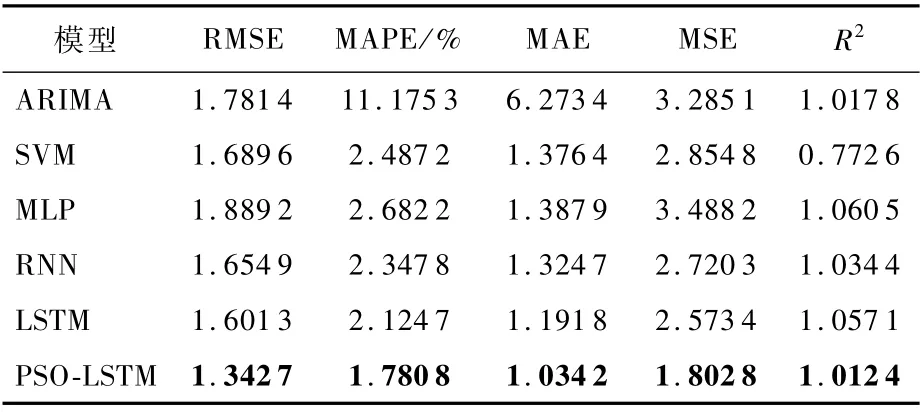
表3 五糧液各模型評價指標比較Table 3 Comparison of var ious models’evaluation indicators for Wuliangye

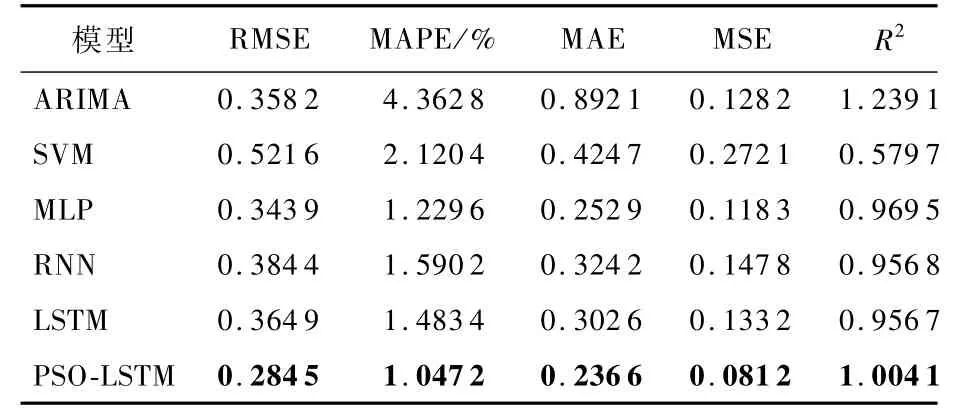
表4 恒隆集團各模型評價指標比較Table 4 Comparison of var ious models’evaluation indicators for Hang Lung Group

4 結 論

針對復雜的股票價格預測問題，本文提出了PSO-LSTM模型，通過自適應學習策略的PSO算法對LSTM 網絡結構進行優化，減少人為因素影響，以提高模型捕獲股票數據特征的能力。本文隨機選取了滬市（浦發銀行）、深市（五糧液）、港股（恒隆集團）股票數據進行實驗。實驗表明相較于統計模型與其他時間序列機器學習模型，PSO-LSTM 模型具有更高的預測精度，并且對于不用類型的股票數據具有一定的普遍適用性。該模型在金融時間序列研究中將具有廣闊的應用前景。