旋轉彈控制耦合的分數階滑模解耦
戴樹濤,陳華兵,程養民,楊宇星
(西安航天動力技術研究所,陜西 西安 710025)
0 引言
導彈武器或運載火箭采用旋轉體制能夠提升穩定性,有利于提高導彈克服諸如推力偏心、起控點散布、質量分布不均勻、隨機陣風等干擾的能力[1]。為提升旋轉導彈的過載能力,因此產生了旋轉導彈雙通道控制,以解決傳統單通道控制的過載能力不足[2]。但是旋轉體制同時也會帶來俯仰、偏航雙通道的交叉耦合[3],這些耦合主要包括陀螺慣性耦合、馬格努斯氣動耦合以及舵系統控制耦合。耦合會對控制系統的工作造成不利的影響,嚴重時甚至會導致失穩,因此解耦成為旋轉彈控制系統設計的首要問題。在這些耦合因素中,運動學耦合造成的通道間耦合往往較小,且隨自旋轉速的變化不大,所以雙通道解耦的重點就是消除舵系統的控制耦合[4]。閆曉勇等人基于一階舵系統模型設計了指令超前補償解耦控制器[5],實現了舵系統的解耦。李永亮通過研究十字型鴨翼旋轉彈模型[6],對一階舵系統模型設計了前置補償器,實現了鴨式舵系統的解耦。總的來說,這些傳統解耦方法的思路都是基于舵系統傳遞函數矩陣,通過前饋補償、指令超前補償等多變量頻域方法設計解耦控制器實現對角占優,使得傳遞函數矩陣的非對角元素為0或者近似為0,從而達到解耦的目的。但以上方法的最大問題在于需要對傳遞函數矩陣進行復雜且計算量較大的求逆運算,如果傳遞函數矩陣的階次較高或者系統模型復雜,求逆操作往往不易實現。而且在求逆計算中,易出現矩陣接近奇異使得求逆運算的結果已不可采用的情況。除此之外,基于頻域方法設計的解耦控制器只能實現系統穩態條件下的靜態解耦,且一旦舵系統參數發生攝動或者自旋轉速產生變化,解耦效果便難以保證。
為解決以上問題,本文基于更為貼合工程實際的二階舵系統模型,通過推導旋轉舵系統的狀態空間表示,采用分數階微積分理論和滑模變結構控制理論來設計舵系統的解耦控制器,以避免對傳遞函數矩陣求逆。仿真結果表明,滑模解耦能夠提升解耦控制系統對參數攝動和轉速變化的魯棒性,采用分數階微積分理論能夠減小滑模控制方法的抖振。
1 舵系統的模型及耦合分析
1.1 舵系統的二階狀態空間模型
為避免自旋造成的不便,旋轉彈的建模往往基于準彈體系,而舵系統是在旋轉的彈體系下生成舵偏角[7],故先將彈體系下的舵系統輸入輸出信號投影到準彈體系下。彈體系和準彈體系下舵偏角的關系如圖1所示。
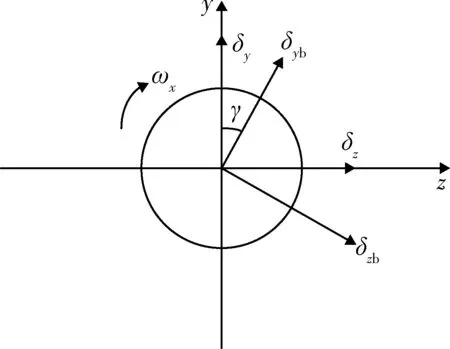
圖1 彈體系和準彈體系下舵偏角關系圖
圖1中δzb和δyb分別為彈體系下俯仰舵偏角和偏航舵偏角,δz和δy分別為準彈體系下俯仰舵偏角和偏航舵偏角。假設滾轉角為γ,由準彈體系到彈體系下的舵系統指令變換關系為
(1)
為了分析問題的簡化,作以下假設:忽略導彈滾轉通道的動態變化過程,并且由于導彈旋轉轉速的變化較緩慢,可假設導彈滾轉速度ωx不變,對式(1)求一階導數如下:
(2)
對式(2)再求導如下:
(3)
彈體系下舵機的系統模型一般表示為二階傳遞函數:
(4)
式中:Ts為舵機的時間常數,μs為舵機的阻尼系數,這2個參數為舵機的重要參數,受舵機硬件水平的限制。則根據式(4)可知彈體系下舵機的輸出舵偏角向量δb=(δzb,δyb)T與舵機的輸入信號δbc之間的關系如下:
(5)
將式(2),(3)代入到式(5),并根據式(1)將指令投影到準彈體系下,可得
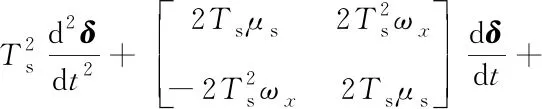
(6)
式中:δ=(δz,δy)T和δc=(δzc,δyc)T分別為準彈體系下的舵機輸出信號和輸入信號。
為了得到準彈體系下舵機的狀態空間模型,選取狀態向量x=(x1,x2,x3,x4)T,各分量如下:
(7)
選取輸出向量y=(y1,y2)T,各分量為
(8)
可得舵機的狀態空間模型為
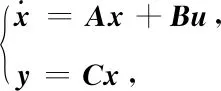
(9)
式中:u為解耦后舵系統的輸入信號,若沒有解耦控制器,則u=δc;
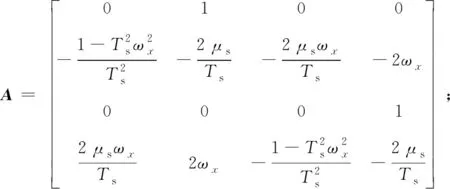
1.2 舵系統的耦合特性分析
為了便于分析舵系統的耦合特性,對式(6)進行拉普拉斯變換,得到準彈體系下舵機傳遞函數矩陣為
(10)
式中:
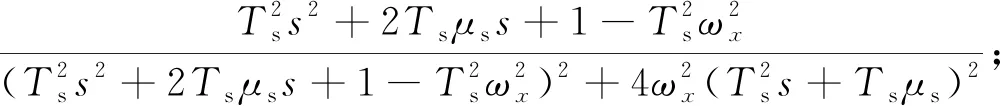
由傳遞函數矩陣可以發現,當彈體的滾轉速度為0時,即彈體不滾轉時非對角元素為0,此時不存在耦合。彈體滾轉使得舵系統的階次由二次變為四次,增加了系統的復雜性,且此時舵系統的頻帶與彈體滾轉速度相關。
為分析轉速對耦合效應的影響,使用Matlab軟件對舵系統模型進行仿真,舵機參數如表1所示。

表1 舵機參數取值
分別給定俯仰舵指令信號為單位階躍信號和頻率為2 Hz,幅值為1的正弦信號,繪制出轉速分別為3,5,10 r/s時的偏航舵響應信號曲線如圖2,3所示。
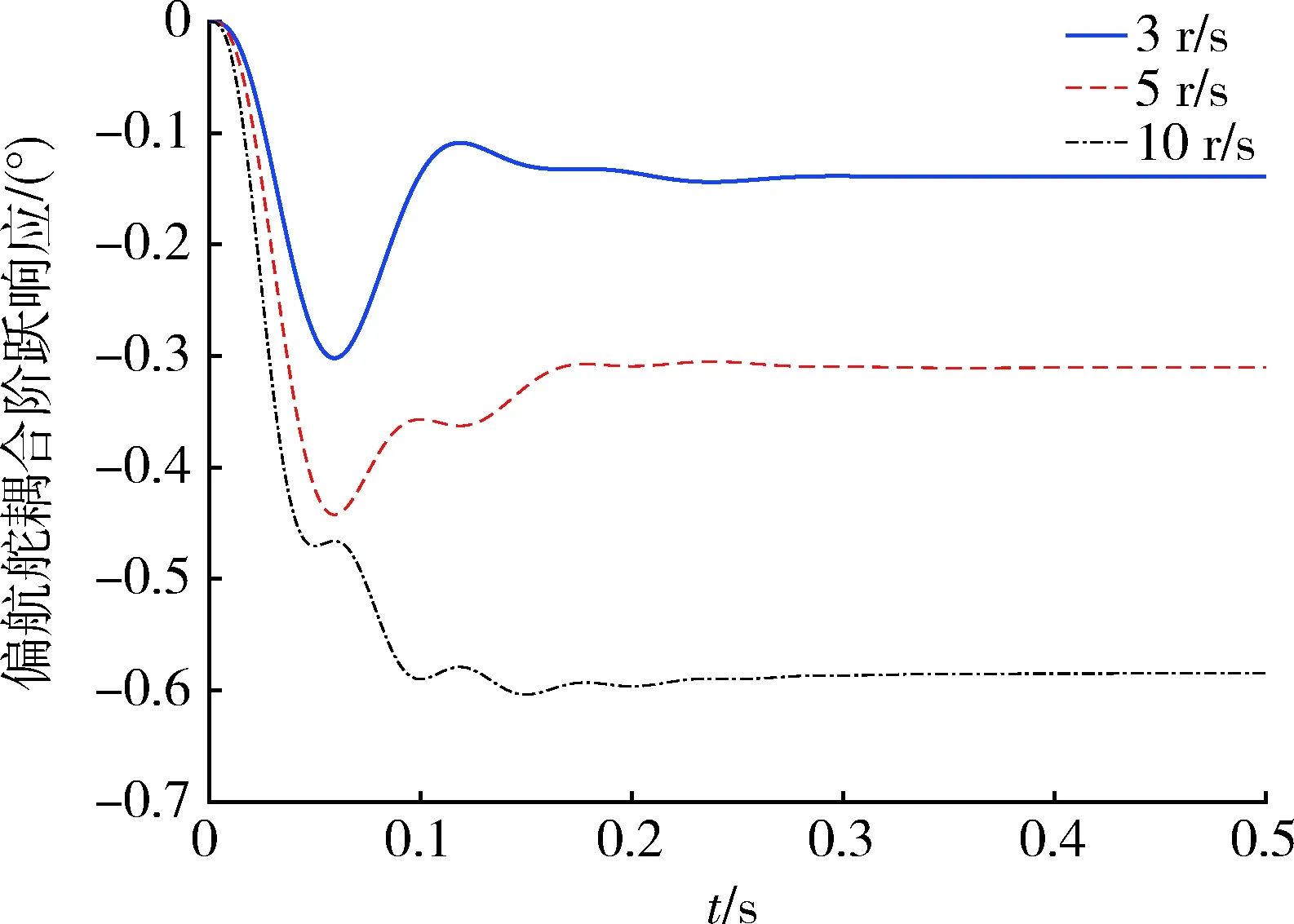
圖2 偏航舵耦合階躍響應
由圖2可得出,轉速越大,控制耦合越嚴重。對本舵機參數而言,轉速3 r/s時穩態耦合量約為15%,轉速5 r/s時穩態耦合量約為32%,轉速10 r/s時穩態耦合量約為60%。

圖3 偏航舵耦合正弦響應
由圖3也能看出轉速越大,耦合程度越大,并且舵系統延遲時間也越長。
綜合以上分析可以得出,控制耦合的程度與彈體滾轉速度呈正相關,且耦合越劇烈,舵系統延時越長。
2 滑模變結構解耦控制器
為改善轉速和參數變化下傳統解耦方法效果差的問題,采用滑模變結構理論設計解耦控制器,其解耦控制結構圖如圖4。
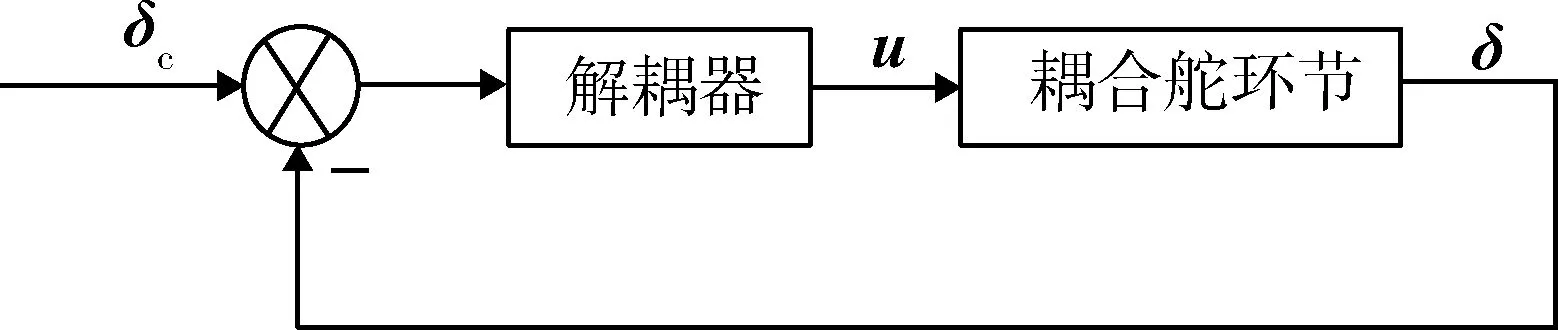
圖4 解耦回路圖
以δc=(δzc,δyc)T為舵指令信號,δ=(δz,δy)T為舵輸出信號。令e1,e2為跟蹤誤差,則e1=δzc-δz,e2=δyc-δy,故解耦控制的目標即使得e1=e2=0。令e=(e1,e2)T,取滑模面函數為
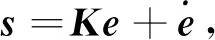
(11)
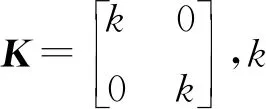
對式(11)求導,可得
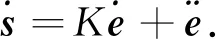
(12)
采用指數趨近律,為減少抖振趨近律中采用飽和函數,飽和函數表達式如下:
(13)
式中:Δ為正數。
設計趨近律如下:
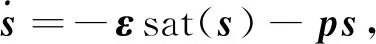
(14)
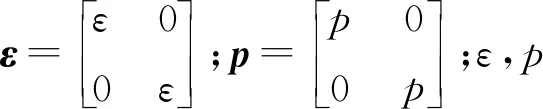
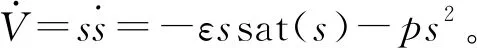
(15)
由式(9)可推得:
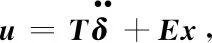
(16)
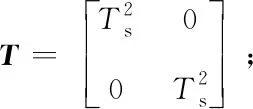
將式(15)與式(16)聯立,可得到設計的滑模控制律為
(17)
3 分數階滑模解耦控制器
滑模控制器雖然具有很多優點,但也存在固有的抖振問題,這不利于工程實際應用。使用分數階微積分算子代替滑模控制器設計中變化劇烈的整數階導數項,有利于減小滑模控制的抖振,因此使用分數階微積分理論對滑模控制器進行優化。
3.1 分數階算子的近似方法
目前,盡管一些學者對分數階微積分控制器做了相關研究[8-11],分數階理論在數學上還是較難直接實現的,無法求得其精確值,主要還是采用有限的整數階微積分近似逼近。Outstaloup A提出了Outstaloup遞歸濾波器的有理化近似法[12],該方法率先提供了一種分數階算子的實現途徑,為其他方法的產生奠定了理論基礎。因整數階微分的幅相特性隨頻率變化,因此在近似逼近時要選定一個頻段。假定濾波頻帶為(ωb,ωh),則可以構造Outstaloup濾波器為
(18)
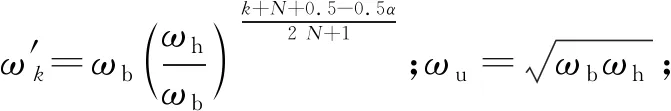
由于該方法的近似效果一般,因此也有其他學者提出了逼近方法,其中東北大學薛定宇教授等人在Outstaloup濾波器的基礎上提出了改進的Outstaloup濾波器法[13]。令
(19)
式中:α為分數階次,0<α<1;b>0;d>0。
對L(s)進行一階Taylor展開,整理可得
(20)
本文采用改進型Outstaloup濾波器來近似分數階算子。
3.2 分數階滑模解耦控制器
取滑模面函數為
s=Ke+Dαe,
(21)
式中:Dα為分數階微分算子,表示求α次導數,0<α<1。對式(21)求導,得
(22)
按照式(14)設計趨近律,并進行類似于前述的推導過程,可得出控制律為
D1-α(εsat(s)+ps)).
(23)
4 仿真校驗
4.1 仿真過程及參數
設導彈自旋轉速為3 r/s,舵機參數如表1所示。需要說明的是,表1中舵機參數的選取不能隨意設置,因為旋轉導彈彈體固有頻率fn、自旋頻率fx和舵系統帶寬fb之間應滿足以下關系[14]:
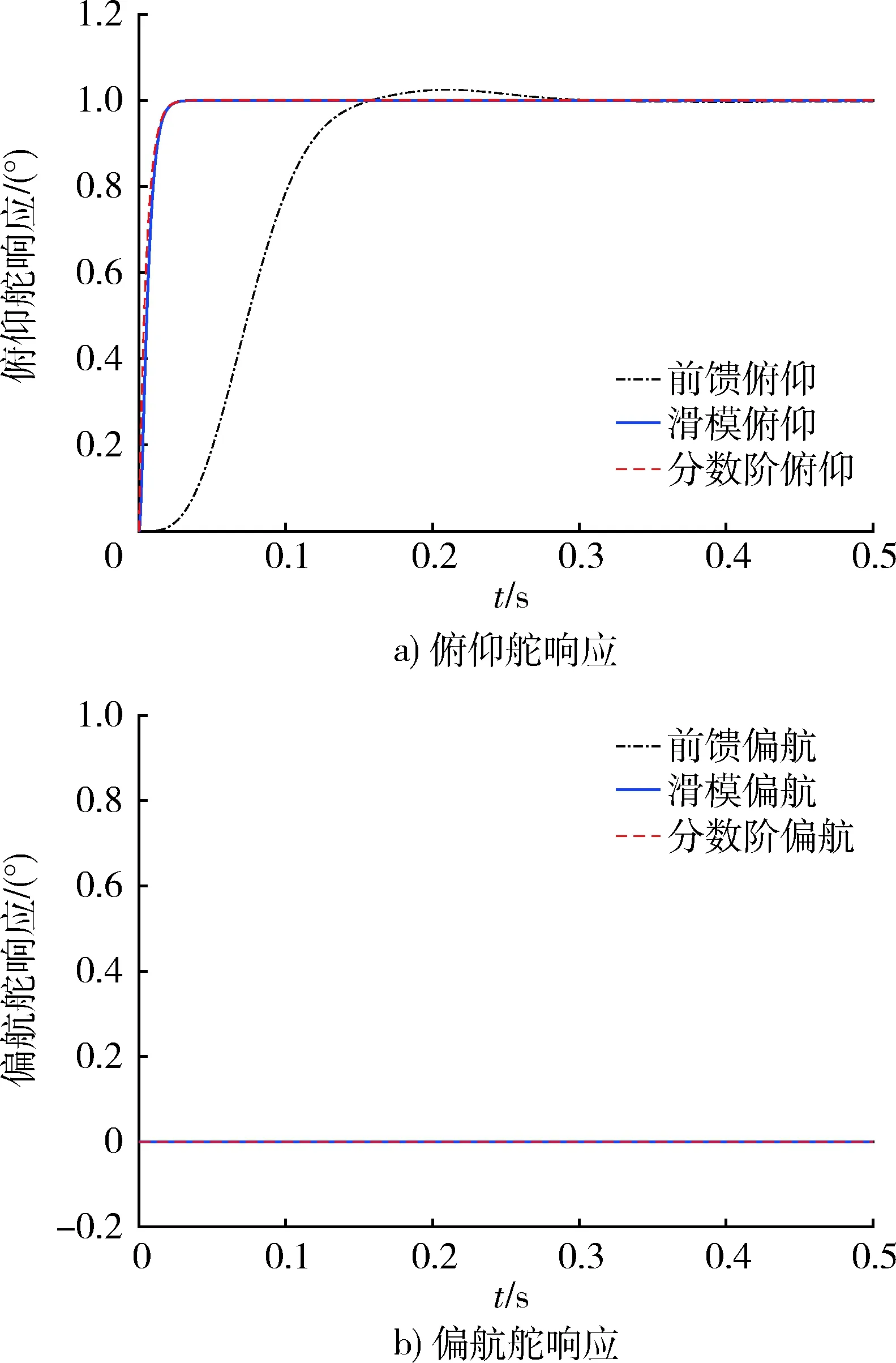
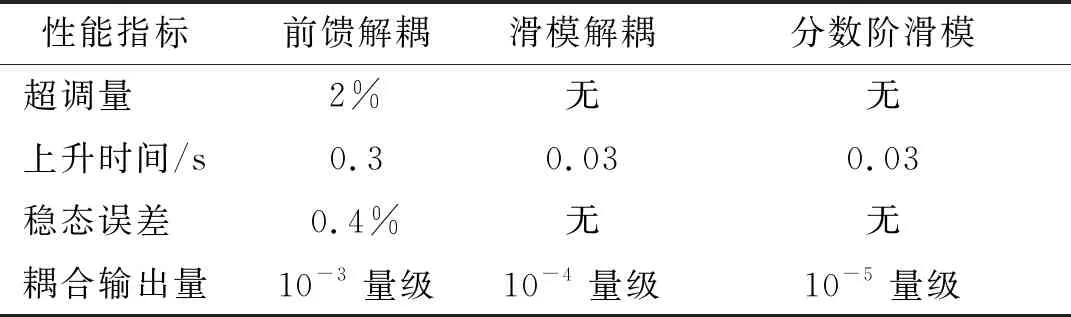
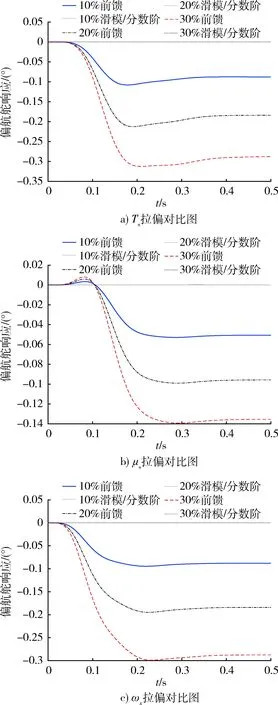
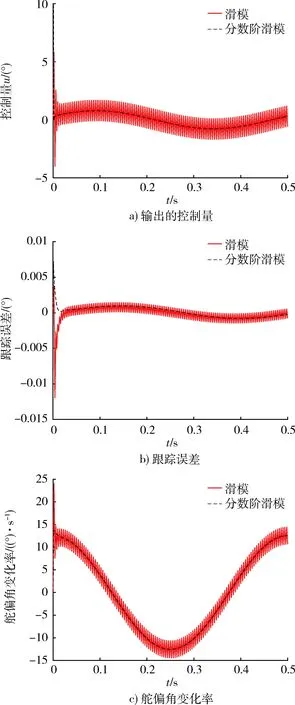
1.8fn (24) 否則會引起系統共振,導致災難性后果。因fx=3 Hz,取fb=8 Hz,則ωb≈50.880 8 rad。 根據二階系統帶寬計算公式[15]: (25) 取阻尼系數μs=0.5,可推出ωs≈40,故Ts=1/ωs=0.025。 按照式(17)的設計思路搭建模型進行仿真,滑模解耦控制器各參數取值如表2所示。 表2 滑模解耦參數取值 按照式(23)的設計思路搭建模型進行仿真,分數階滑模解耦控制器各參數取值如表3所示。 表3 分數階滑模解耦參數取值 將俯仰舵指令信號設為單位階躍信號,偏航舵指令置0,將前饋解耦方法、滑模解耦方法、分數階滑模解耦方法3種方法舵輸出信號的仿真曲線繪制如圖5,并將圖5的定量分析結果繪制如表4。 圖5 標準參數值下3種解耦方法響應對比 表4 圖5結果對比 由圖5和表4可知,滑模解耦和分數階滑模解耦能夠消除響應的超調量和穩態誤差,響應速度僅為0.03 s,其解耦精度比傳統前饋解耦更高。 將俯仰舵指令信號設為單位階躍信號,偏航舵指令置0。為驗證滑模解耦控制器對參數攝動的魯棒性,分別將舵機的時間常數、阻尼系數和彈體轉速拉偏10%,20%和30%,將前述3種方法的偏航舵耦合輸出信號的仿真曲線繪制如圖6,定量結果如表5。 圖6 參數拉偏下3種解耦方法偏航舵耦合對比 由圖6和表5可知,前饋解耦方法對參數變化無魯棒性,滑模解耦能夠抑制30%的參數偏差所引起的不利影響。還可發現Ts和ωx的變化對前饋解耦的效果影響較大,而μs的變化對前饋解耦的效果影響較小。 表5 圖6參數拉偏下耦合輸出量對比 圖7 兩種滑模方法的結果對比 由圖7可知,采用傳統滑模方法,穩態控制量抖振幅值為1左右,舵偏角變化率抖振幅值為2左右,這些抖振均不利于舵系統安全穩定工作。采用分數階滑模解耦能夠消除控制量和舵偏角變化率的抖振,以保護舵系統,且能夠減小跟蹤誤差,提高跟蹤精度。 本文針對旋轉彈箭雙通道舵系統的解耦問題,為解決傳統頻域補償方法需要求逆和對參數攝動魯棒性差的問題,設計了滑模解耦控制器,并且為抑制滑模方法的抖振,引入了分數階微積分理論,設計了分數階滑模解耦控制器。仿真結果表明,所設計的解耦控制器能夠滿足舵機系統的解耦要求,且能夠解決傳統解耦方法存在的問題,具備一定的工程應用價值。

4.2 仿真結果及分析
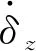

5 結束語

