教練機飛行性能指標論證方法研究

蔣盼盼，劉 卓

（航空工業洪都，江西 南昌，330024）

0 引言

教練機作為飛行員訓練的主要裝備，很少直接參加空戰或擔負空中打擊任務，其焦點是將飛行學員快速培養成技能嫻熟的飛行員，因此其飛行性能指標（下文簡稱“性能指標”）論證方法與戰斗機的相比，既有相似性又存在顯著不同。現代教練機是系統配套、體系化發展的[1]，飛行員過渡到更高學習階段需要經歷一段過渡轉換時間[2]，如果該階段與前一階段飛機性能銜接合理、過渡光滑，飛行員狀態轉換時間會明顯縮短，訓練效率會更高。這也意味著，教練機性能指標論證除了需考慮使命任務要求、經濟性要求、未來較長時間內的前瞻性和可擴展性要求外，還需著重考慮教練機在訓練體系中的銜接性要求[3]，以期實現技能“正遷移”和高效訓練。

教練機作為一種訓練裝備，其相對目標機（本文的目標機指教練機向上銜接的機型，如基礎教練機的目標機為高級教練機，高級教練機的目標機為戰斗機等）來說擔當從屬作用，而目標機的發展演化和更新換代，本身也具有特有趨勢，因此教練機性能指標論證不能針對單機平臺進行定性描述，而應將教練機特性與目標機特性關聯起來，尋找一種系統性量化方法，為確定科學、合理的教練機性能指標提供決策依據。目前雖有公開的文獻針對通用飛機/戰斗機的性能指標進行論證，但尚未有針對教練機性能指標論證方法的研究，如代桂成等[4]參考國內外多個超輕型飛機適航標準，提出了超輕型飛機性能要求。楊華保[5]基于原準機數據的修正采用重量分析方法對戰斗機的性能指標進行了分析論證。黃俊等[6]以訓練效能為目標函數對高級教練機的性能指標進行了優化。以上相關研究雖為論證教練機性能指標提供了借鑒和參考，但其或側重于單機平臺，或側重于類比，或側重于性能指標的優化，未介紹關注銜接性的性能指標從無到有的論證過程。基于此，本文提出了一種系統性定量分析教練機性能指標的方法——關聯預測法，其綜合考慮了以下三個方面：一是教練機之間的體系定位和配套能力，二是與作戰飛機的銜接性，三是未來較長時間內的前瞻性和可擴展性。該方法以最優化準則為核心，能夠合理論證滿足當前和未來需求的初步教練機性能指標，為后續教練機性能指標的進一步優化和確定提供可靠的初始數據。

1 關聯預測法理論分析

關聯預測法的研究對象不再是單機平臺，而是相互之間有關聯的“飛機對”。方法的本質是關注教練機與目標機間的協調性，以及這兩類飛機特性之間的定量聯系。通過歷史時段教練機與目標機的特性聯系總結并檢查規律，再根據選定的預測階段目標機特性值，將規律延伸至未來，獲得教練機性能指標預測值。

1.1 數學模型

為了系統性分析教練機與目標機特性之間的聯系，首先需確定教練機與目標機“飛機對”集合和規范化的權重系數矢量。“飛機對”可理解成為了使用目標機，而利用該教練機系統培訓飛行員的教練機和目標機。每一“對”都對應有自己的權重系數，且與教練機的使用數量、服務期成比例。該方法的核心是確定教練機性能指標矢量的零次最佳一致逼近，可用如下形式描述：

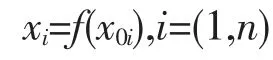
其中：xi——預測的未來時段教練機與目標機對于特性i的關聯系數均值；

x0i——歷史時段教練機與目標機對于特性i的關聯系數均值；

n——教練機特性集合中的特性個數。

根據上式可以得出：

1）從形式上說，該方法在某種意義上是教練機發展所要求的；

2）從方法上說，該方法是目標預測優勢和搜索方法的要素結合；

3）從時間上說，該方法所預測的結果應該是短-中期（5～15年）的，因為預測結果的可信時間期限應該不短于研制教練機過程的時間周期（平均5年），且不超過目標飛機更新換代周期（10～15年）。

1.2 方法設計步驟

關聯預測法主要由四部分內容構成：原始數據庫的建立，相關性檢查，構建關聯系數及趨勢，預測飛行性能值。

1.2.1 原始數據庫的建立

1）確定要預測的教練機性能矢量構成

選定要研究的教練機性能參數，也就是矢量={x1i},i=1,2,L,n（n為性能參數總個數），該集合可能受以下幾個方面的支配：必須準備估算教練機訓練效能用的初始數據；對性能參數的計算方法研究的充分程度；歷史數據可查性等。

2）形成教練機和目標機及其“飛機對”的客觀歷史數列

選定教練機{X1i}，i=1,2,L,N1，它與一定的目標機{X2i},i=1,2,L,N2有關，其中N1，N2表示歷史時段教練機總數和目標機總數，X1i、X2i表示歷史時段教練機型號和目標機型號。從中分出N對“飛機對”，將這些“飛機對”與特定時間聯系在一起，就構成了“飛機對”的客觀歷史數列。

基于以下兩點考慮，客觀歷史數列選擇前期50年：

（1）如前所述，預測是短-中期（5～15 年）的結果；

（2）為保證預測結果的精度和可靠性，歷史時段應比要預測的未來時段長好幾倍。為便于分析和構成后續的預測并檢查其正確性，以10年分段，并且將N對“飛機對”分成兩個數列——前4個10年的N0“對”為教練數列，最后一個 10年的Nk“對”為檢查數列。

3）構成“飛機對”的性能矢量數據庫

使用上一步選取出來的N對“飛機對”，以及它們協同使用的時間點，查找或計算n個性能值：{x1ij},{x2ij},{tij}，i=1，2，L，n，j=1，2，L，N， 其中x2ij為目標機性能矢量，tij為性能指標x1ij與x2ij協同使用的時間點。所有飛機的同類性能應按同一方法計算，否則由于計算誤差的差異，這些性能的未來預測趨勢可能逐漸失真。

1.2.2 相關性檢查

相關性檢查目的是理清“飛機對”的性能指標聯系。數據庫建立好之后，就可以定量估算教練機與目標機性能指標間的規律關系。一般情況下，教練機性能指標矢量與其成對的目標機性能指標矢量={x2i}，i=1，2，L，n的聯系，可表示為=M·其中M為關聯矩陣，由此可以得出，教練機的任意性能指標x1P，p=1，2，L，n與目標機特性集之間可認為是線性關系：

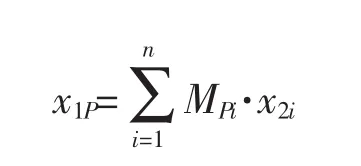
教練機和目標機性能存在線性關系的假設，可以通過相關性檢查進行檢驗。基于相關分析法，分析歷史時段中每個10年段相同性能指標下教練機與目標機間的相關性系數，并與對應于選定的置信概率的相關系數門檻值相比較。相關解析結果分析表明，教練機和目標機同樣性能指標間，大多數情況下可發現顯著的相關性，即第一次逼近時，矩陣M集中在對角線上，因此可認為教練機的特性與目標機的對應性能指標成正比。

1.2.3 構建關聯系數和趨勢

1）形成關聯系數數組

將性能指標的絕對值轉化成它們的比值，即關聯系數kij=x1ij/x2ij，i=1，2，L，n，j=1，2，L，N。 在大多數情況下，相對于飛機性能與時間之間的關系，關聯系數與時間的關系更穩定和單調一些。

2）淘汰非典型“飛機對”的關聯系數

針對各性能指標，分析每個10年段出現的關聯系數相對均值的正態最大偏差值τi,i=1,2,L,n，并與選定置信概率下的偏差門檻值τT進行比較，淘汰滿足τi≥τT的“飛機對”，使預測有更充分的依據。

3）構成關聯系數趨勢

去掉淘汰掉的關聯系數值，構成“飛機對”性能指標關聯系數的動態數列。利用篩選后的教練數列構建線性趨勢，Ki=aiT+bi，i=1，2，L，n， 其中時間T取各 10年段的平均年份進行計算，Ki表示在T時刻由趨勢確定的對于特性i的關聯系數值，ai，bi分別表示線性比例系數和常數分量。

由于計算的性能值有誤差，也就是說關聯系數的計算有誤差，而“飛機對”協同使用的時間也不能認為是準確的，所以不能使用常用的最小二乘法計算ai、bi，i=1，2，L，n。不同構建方法的分析結果表明，此時采用 wald 回歸法計算ai，bi，i=1，2，L，n最為合適。

4）檢查趨勢形式選定的可靠性

使用wald檢驗法檢驗趨勢選定的可靠性，具體公式如下：

其中，Nl——第l（l=1,2,3,4）個10年段內的“飛機對”數量；Tl——第l個10年段的平均年份；kij——第l個10年段中關于特性i的第j個關聯系數；F0是給定置信概率下的F分布值。

如果上式的檢查結果否定，就返回上一步，重新選定一種線性趨勢，并計算ai、bi,i=1，2，L，n。

5）檢查趨勢的預測性能

1.2.4 預測教練機性能指標矢量

基于戰術技術任務書或通過科學預測的方法選定未來目標機性能指標矢量={x2Yi}，i=1,2,L,n，再根據預測的關聯系數值KYi=aiTY+bi,i=1,2,L,n，獲得零次逼近的預測階段教練機性能指標矢量={x2Yi×KYi},i=1,2,L,n。

通過關聯系數得到的零次逼近的教練機性能指標矢量，著重考慮了教練機在訓練體系中的銜接性要求，不僅反映了教練機解決傳統問題的能力，也反映了現有教練機在訓練效能方面已實施的方法和措施。但是，關聯預測法的分析結果具有綜合性特點，其無法考慮更特殊情況，特別是對形成教練機性能矢量非常關鍵的那些因素，如飛行員訓練大綱的特點，不同國家和不同代飛機的差別很大；還有教練機戰技任務書中包含的特殊要求（如成本限制或某些系統選定限制）。因此，根據先進定位的原則，后續需對零次逼近的教練機性能指標矢量作進一步優化和最終確定。

2 算例分析

考慮到飛行性能參數以及“飛機對”客觀歷史數據眾多，為更快速、有效的運用該方法，本文在Matlab平臺上對該方法進行算例數值計算。以研究2015年左右的配裝渦槳發動機的基礎教練機為例，相應的目標機選定為某型高級教練機。

根據新型基礎教練機的需求定位、使用特點及可能得到的用于構建基礎教練機和目標機 “飛機對”集合的統計數據，算例選取的未來基礎教練機主要特性包括失速速度(放襟)、實用升限、海平面最大爬升率等9個參數。圖1～圖2是2015年左右失速速度（放襟）和海平面最大爬升率關聯系數的計算結果，KI-KV為回顧歷史時段的關聯系數均值。圖1中所顯示的失速速度(放襟)關聯系數值增大，主要是由于目標機大迎角飛行能力增強，左邊界能力顯著提高。圖2中所顯示的海平面最大爬升率關聯系數值減小，主要是由于目標機機動性能增強及發動機可選性更大，計算結果與實際情況相符。

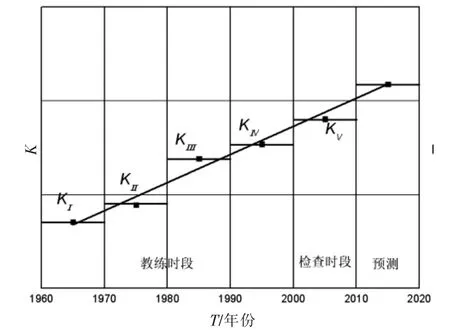
圖1 失速速度(放襟)關聯系數隨時間變化趨勢

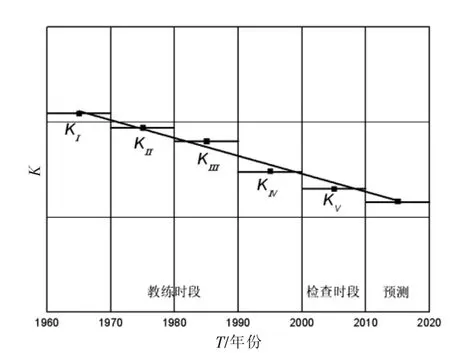
圖2 海平面最大爬升率關聯系數隨時間變化趨勢

為了進一步驗證預測結果的合理性，統計了國外同時期同類渦槳基礎教練機的飛行性能參數，獲得各性能參數參考區間[7]，如表1所示。

從表1可知，預測的失速速度(放襟)、海平面最大爬升率性能指標與同時期同類型的教練機基本相當，可以認為該預測結果相對準確，進一步檢查了預測方法的合理可信性。

3 結論

通過對教練機性能指標論證特點的分析，建立了一種系統性量化分析未來教練機性能指標的方法，并進行了算例計算，得到了以下結果：

1）該方法以最優化準則為核心，充分考慮了教練機性能指標在訓練體系內的銜接性特點以及未來較長時間內的前瞻性和可擴展性。

2）該方法預測的性能指標科學、合理，可為性能指標后續進一步優化和最終確定提供可靠的初始數據。