基于PSO 算法的有限元仿真模型
張曉娜 常樂冉 吳煒 王一晴 山東科技大學
引言
標槍運動是我國一貫較為重視的一項運動,標槍競技的勝負裁決是根據投擲標槍的距離所給出的。本文主要采用粒子群算法(PSO)進行標槍投擲最佳距離的求解,通過迭代尋求全局最優解,較為精確地獲得標槍投擲的最佳距離以及相關角度、速度的關系。在了解標槍幾何形狀和尺寸參數的基礎上,構建標槍的有限元模型,同時借助計算機仿真獲得最優投擲距離和角度。
1 計算標槍投擲距離
在無風的前提下,排除標槍飛行中所受空氣影響,從運動學角度對標槍飛行軌跡進行分析。假設圖中投擲者出手高度為ho,初速度為vo,投槍角為透出器械,標槍沿一條曲線運動,該曲線經過與A 點同高的B 點并落于地面上的C 點。
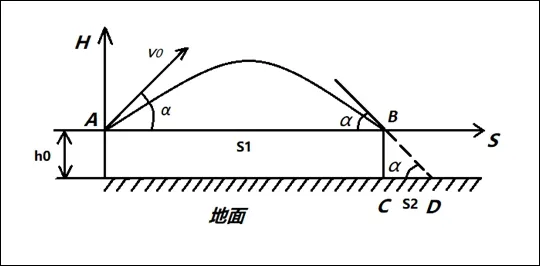
圖1.標槍投擲飛行軌跡
根據運動學可知,在不考慮空氣阻力的情況下,這條曲線近似為拋物線。根據拋物線軌跡來分析標槍的運動,把運動軌跡分為AB 段和CD 段,即S1 和S2。標槍由A 點投出,經過最高點而落到與A 點同高的B 點。根據運動學的斜拋運動可知,水平投擲距離為:

標槍由B 運動到D 的水平距離S2,可以近似的把曲線BC 看成是直線,其斜角近似等于出手角度,因此得:

所以,總的投擲距離為:
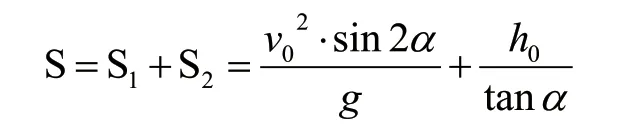
根據題目中給出的投擲出手速度為29.70m/s、出手角為36.6°、初始攻角為-0.9°,可以計算出投槍角a=35.7°,將以上數據帶入3-3式,即可得出標槍投擲距離約為70.24m。
2 PSO 模型建立
通過粒子群算法,根據鳥類尋食的仿生學,結合個體的最優解和群體的最優解不斷地迭代來尋找區域的最優解。位置限制[28,44],取初始種群N 為50,迭代次數為100,在28~44 內隨機生成一個50x1 的數據矩陣,每次搜尋都需要將當前的適應度和最優解同歷史的記錄值進行對比,如果超過歷史最優值,則更新個體和種群的歷史最優位置和最優解。
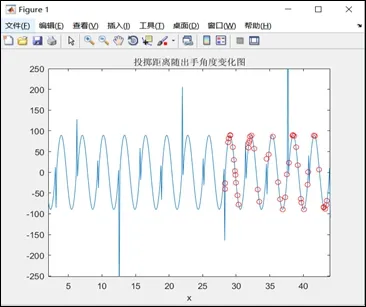
圖2.投擲距離變化圖
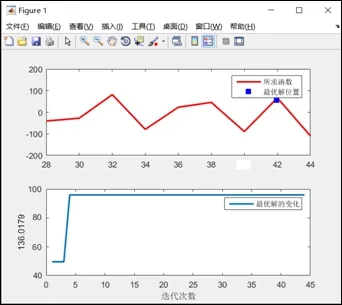
圖3.標槍投擲最佳距離
3 有限元模型的建立
首先根據已知的標槍尺寸確定標槍的幾何形狀,標槍的結構分為槍頭、槍身及把手。根據其物理模型對每部分的尺寸進行設置,并確定標槍質量、形心位置等,利用有限元法對幾何模型進行網格式劃分,創建標槍的有限元模型。

圖4.標槍的有限元模型和空氣包模型
在建立了標槍的有限元模型以后,在其周圍建立一個 2640 mm× 37mm×2mm 的長方體幾何模型;其次,對該空氣氣流場定義單元類型 (SolidElement)和材料屬性(Null),假設標槍為剛體,其材質設定為合金材料;再次,對其進行有限元網格的劃分。同樣,所有的單元也為四邊形單元,共劃分了195360 個單元,模型如圖所示。
計算機仿真
將標槍的有限元模型和空氣包模型建立完成以后,最后對這一系統模型進行第二次的參數設置。在參數設置的過程中,將對空氣采用Euler 單元,對標槍采用Lagrange 單元,它們之間的耦合采用*CONSTRAINED_LAGRANGE_IN_SOLID 命令來實現。
在對標槍一空氣包建立有限元模型以及對其賦予材料、單元屬性、邊界條件、初始條件以及風對標槍的作用力以后,使用ANSYS/LS-DYNA 求解器對其進行求解。
在本文的研究中,對標槍飛行的計算機模擬均是在考慮空氣阻力的情況下進行的。通過給定空氣的密度、粘性系數和狀態方程,利用流一固耦合的方法來模擬標槍在空氣內的運動情況。
由以下模擬結果可以看出,風對標槍的飛行遠度的影響比較顯著。在其它初始條件`定的情況下,隨著逆風風速的增大,標槍的飛行遠度呈現出減小的趨勢。但是,在同樣的逆風風速下,當初始條件中的出手角度不斷增大,標槍的飛行遠度又不斷增加,當出手角度增大到42 度時,它的飛行遠度又有所減小。由此也可說明,在空氣阻力的作用下,標槍的最佳出手角度并不是45 度。
標槍投擲最優解
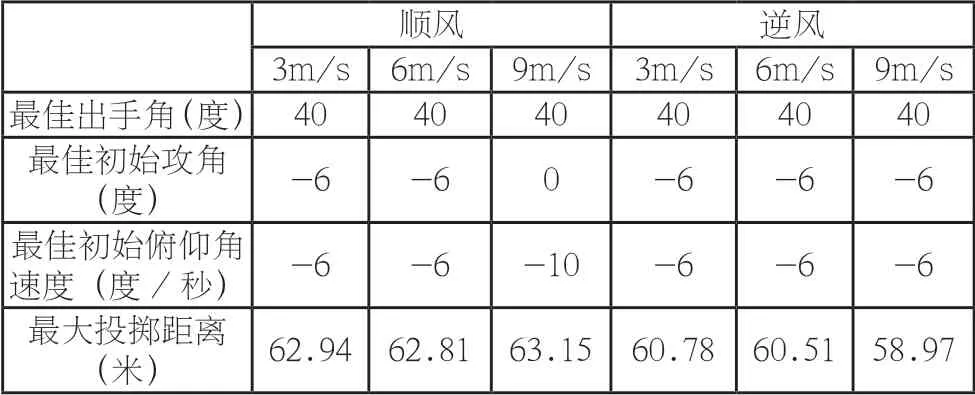
表1
4 標槍投擲規律的總結
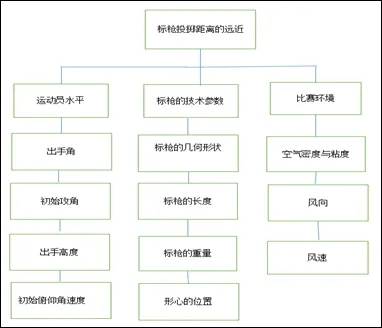
圖5. 標槍投擲影響因素

圖6.標槍初速度對投擲距離的影響
分析影響標槍投擲距離的相關因素,主要從運動員、標槍參數、比賽環境進行考慮,基于標槍投擲距離模型的構建,得出影響標槍飛行距離的因素具體有以下幾點:
(1)在其他初始條件不變的情況下,標槍飛行距離隨初速度vo增加而增加。圖中標槍的出手角度為44°,初始俯仰角速度,初始攻角均為零,可見標槍的初速度增加1m/s,標槍的飛行距離增加4-5m,當初速度繼續增加時,飛行距離有繼續增大的趨勢。
(2)在其他初始條件不變的情況下,標槍在出手角度為0°~44°的范圍內,隨著出手角度的增加,標槍的飛行距離基本上是不斷增加的。但是,從模擬結果上來看,當出手角度大于44°時,在空氣阻力的影響下,標槍的飛行距離會由最大開始下降,所以標槍的最佳出手角度大約在44°左右。

表2
表2.標槍的初始攻角與初始俯仰角組合對標槍飛行距離的影響
(3)在其他初始條件不變的情況下,且出手角度一定時,初始攻角和初始俯仰角速度的組合會影響標槍飛行距離,其中最佳組合為“,當初始條件偏離這一組合式,標槍飛行距離有所減小。
(4)在其他初始條件一定的情況下,初始攻角的變化對其飛行距離的影響并不顯著,但是,在問題三種所討論的初始攻角與出手角度的不同組合中,其中最佳組合為“”時,標槍的飛行距離最遠,達到91.72m,當初始攻角和出手角度的組合偏離這一組合時,飛行距離有所減小。
(5)風對標槍的飛行距離的影響較為顯著。根據第四問的計算結果進行分析,對于逆風而言,在其他初始條件一定的情況下,隨著逆風風速的增大,標槍的飛行距離呈現出減小的趨勢。但是,在同樣的逆風風速下,當初始條件中的出手角度不斷增大,標槍的飛行距離有不斷增大,當出手角度AO增大到44°時,它的飛行遠度有所減小。

