賦值Banach代數的錐b-度量空間中的公共不動點定理

(昭通學院 數學與統計學院，云南 昭通 657000)

1 預備知識

不動點理論已經越來越廣泛的應用于當今科學技術的發展中，由古典的Banach壓縮映像原理所產生的不動點理論已經不能滿足發展的需求了，于是出現了各種推廣，尤其是錐度量空間[1]，錐b-度量空間[2]等. 然而，文獻[3，4]發現錐度量空間與度量空間之間存在等價關系. 直到2013年，文獻[5]定義了賦值Banach代數的錐度量空間，并舉例證明了這種空間與度量空間是不等價的. 因此，有關這類空間不動點理論與應用是非常有價值的. 本文主要是在賦值Banach代數的錐b-度量空間中，探究兩個單值擴張映射的公共不動點定理，本文的結論推廣了文獻中的許多重要定理.

假設A為實Banach 代數，即A是具有乘法運算的實Banach空間，其運算具有如下性質， 對任意的x,y,z∈A,α∈R:(1)(xy)z=(yz)(2)x(y+z)=xy+xz以及(xy)z=xz+yz

(3)α(xy)=(αx)y(4)‖xy‖=‖x‖‖x‖[16].

本文總假設Banach代數A具有單位元 (即乘法單位元)e使得對?x∈A有xe=ex=x.元素x∈A稱為可逆的，如果存在一個元素(稱為它的一個逆元)y∈A使得xy=yx=e.x的逆元記為x-1，文[16].

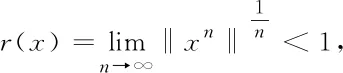
注1[16]若r(x)<1，則‖xn‖→0(n→∞).

定義1[5]設A為Banach代數，θ和e分別是E中零元和單位元，P是A的一個非空閉子集，R+為非負實數集. 若滿足(1){θ,e}∈P;(2)?a,β∈R+?aP+βP?P; (3)P2=PP?P; (4)P∩(-P)={θ},則P稱A是中的錐. 對于錐P?A，定義≤半序如下:即?x,y∈A,y-x∈P,則x≤y;x0，使得θ≤X≤Y?‖x‖≤K‖y‖，則稱錐P為A中正規錐，其中滿足條件的最小正數K稱為P的正規常數.

定義2[2,6]設X是一個非空集合，s≥1為給定的實數，若d:X×X→A映射滿足

(i)θ≤d(x,y)對一切x,y∈X.d(x,y)=θ當且僅當x=y;

(ii)d(x,y)=d(y,x)?x,y∈X;

(iii)d(x,y)≤s[d(x,z)+d(z,y)],?x,y,z∈X.

則d稱X是的一個錐b-度量. (X,d)稱為賦值Banach代數的錐b-度量空間.

定義3[2,6]設(X,d)為賦值Banach代數的錐b-度量空間，x∈X且{xn}n≥1是X中的一個序列，則

(i) 若對任意的c∈intP，存在正整數N，使得對所有的n,m>N，d(xn,xm)?c，則稱{xn}n≥1為Cauchy列;

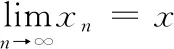
(iii) 若X中的每……