一種井眼軌跡不確定性方法的可視化研究與應用
龔大洪, 陳元鵬, 楊文娟, 楊金生, 王志玲, 張樹義, 馬鴻彥
(1中國石油集團渤海鉆探工程有限公司定向井技術服務分公司 2中國石油渤海鉆探工程技術研究院 3中國石油集團渤海鉆探工程有限公司第五鉆井工程分公司 )
在鉆井過程中井眼軌跡的延伸是一個動態的過程,如果想實時監控井眼軌跡并且對其有個更直觀的認識,則在實現井眼軌跡三維可視化的基礎上通過合理的誤差模型進一步實現三維井眼軌跡誤差橢球可視化對叢式井井眼防碰或救援定向井連通等具有很好的指導意義[1-7]。
目前,運用最為廣泛的井眼軌跡不確定性誤差描述模型有系統誤差模型和ISCWSA誤差模型。系統誤差模型為Wollf[8]和 Wardt于1981年提出的井眼軌跡不確定性分析模型 ,簡稱WdW模型,該模型只提出了六個誤差源,更適用于研究基于陀螺類測斜工具測量垂直井和中等斜度井時系統誤差引起的井眼位置不確定性,具有一定的局限性。ISCWSA誤差模型為井眼測量精度工業導向委員會通過的一種誤差模型,它以Williamson[9]于2000年提出的基于磁性儀器的誤差分析模型為基礎并且還在不斷的完善,該模型提供了井眼軌跡不確定性分析的數學框架,能綜合考慮系統誤差、隨機誤差和全局誤差,被廣泛應用到石油行業中。
一、 ISCWSA誤差模型及測量誤差源分析
1. ISCWSA模型
磁性測量工具測量的井眼軌跡受到很多誤差項的影響,這些誤差項可以歸集為幾個大的誤差源且這些誤差源是相互獨立的,ISCWSA模型假設誤差源在數理統計上服從正態分布,那么在磁性測量工具測量的井眼軌跡上的每個測點的誤差源確定該點的其中一個誤差。將誤差與井眼軌跡三維空間位置相結合,就能用向量把誤差表達出來。井眼軌跡上連續兩個測點的位置向量用計算位移來表示,定義磁性測量工具測量的井眼軌跡上第k-1個測點和第k個測點之間的位置增量為Δrk,則第l個測段的第k個測點上(觀察點以上的測點)由第i個誤差源引起的誤差為:
(1)
式中:ei,l,k—第i個誤差在第l個測段第k個測點NEV軸導致的位置矢量標準差;σi,l—第l組測量第i個誤差源的標準差;pk—第k個測點上的測量矢量,p=[DIA]T;?p/?εi—第i個誤差對測量矢量的影響(一個3×1向量),即誤差的權重函數;dr/dp—測量向量p對要求點井眼位置矢量(NEV軸)r的影響(一個3×3矩陣)。
屬于第L個測段的觀察點K處第i個誤差源引起的誤差為:
(2)
2. 測量誤差源分析
井眼誤差大致可以分為三種類型:系統誤差、隨機誤差和全局誤差。
2.1 系統誤差及其對應權重函數
在測量井眼軌跡的過程中系統誤差又可以再次劃分為已定系統誤差和未定系統誤差。已定系統誤差的方向、大小是已知的。未定系統誤差由于其方向未知,大小也未知,所以一般情況下只能計算范圍,故已定系統誤差可以進行修正,而未定系統誤差則不能進行修正。
2.1.1 MWD傳感器誤差權重函數
MWD共有12個傳感器誤差源,每個誤差源對應一個權重函數向量,可通過對井斜角、方位角求誤差源偏導數獲得。以X軸重力加速度計的偏移誤差和X軸重力加速度計的刻度誤差為例,通過偏微分求導,從而得到修正后的權重函數ABIX:
(3)
2.1.2 儀器不居中誤差權重函數
儀器不居中誤差可以細致的歸為底部鉆具組合垂曲誤差項和徑向不對稱誤差項兩類。底部鉆具組合垂曲只影響井斜角的測量,其大小與垂直于鉆具組合的重力分量成正比,底部鉆具組合垂曲誤差項的權重函數:
(4)
徑向不居中誤差項認為在X,Y軸上存在相互獨立且固定的徑向不對稱誤差,它們在高邊和側向方向上的分量分別導致井斜角誤差和方位角誤差為:
(5)
(6)
2.1.3 鉆具磁干擾誤差權重函數
磁方位角誤差項權重函數為:
(7)
軸向磁干擾誤差項權重函數為:
(8)
2.1.4 深度刻度系數誤差權重函數
刻度誤差權重函數為:
(9)
2.2 隨機誤差及其對應權重函數
隨機誤差通過多次測量估算平均值,這個平均值又稱為隨機誤差限。參考誤差權重函數為:
(10)
2.3 全局誤差及其權重函數
磁偏角固定數值誤差項權重函數:
(11)
磁偏角水平磁場強度(變值)誤差項權重函數為:
(12)
磁傾角誤差項權重函數為:
(13)
總磁場強度誤差項權重函數為:
(14)
拉伸類型誤差項權重函數為:
(15)
二、井眼軌跡不確定性誤差橢球的計算
在每個誤差項權重函數已經被建立的基礎上,就能夠用向量的形式將每個誤差項所產生的誤差表示出來,然后根據概率統計相關知識建立協方差矩陣并得出誤差橢球來表達井眼位置的不確定性。
將隨機誤差、系統誤差、全局誤差三種誤差類型相加,就能算出井眼軌跡上任何測點的總的位置不確定性的協方差矩陣為:
(16)
三、誤差橢球的三維可視化
用Python語言對ISCWSA誤差模型進行描述。根據以上推導公式,把ISCWSA誤差模型轉化為算法并實現在計算機上,井眼軌跡計算采用最小曲率法。整個程序采用模塊化面向對象編程模式,程序的靈活性和可重復利用性強,如圖1。
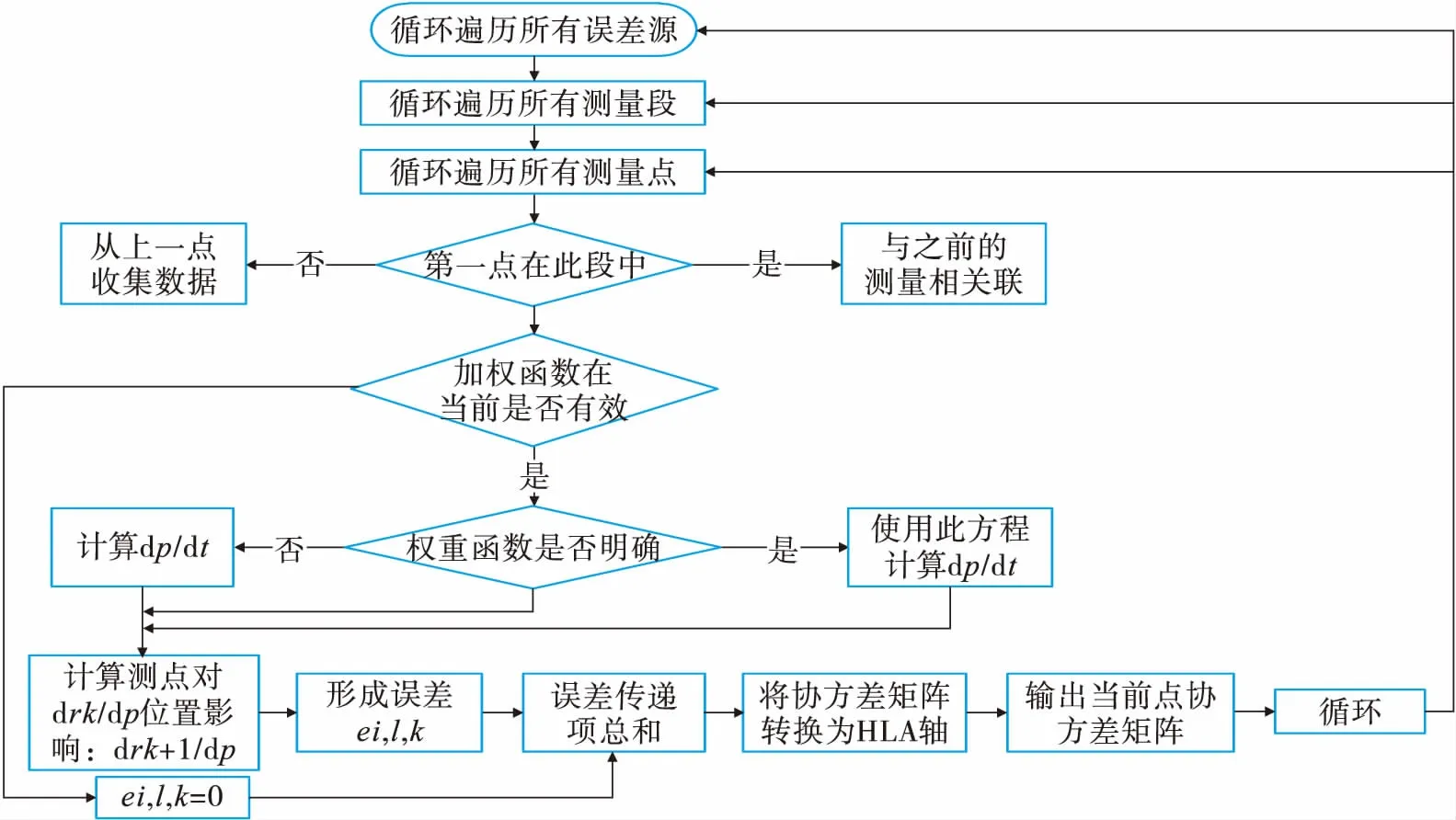
圖1 ISCWSA求井眼軌跡不確定性算法流程
由于誤差橢球半軸相對于井深來說太小,為了能直觀的在三維空間下顯示誤差橢球,在誤差橢球三維可視化的過程中一般需要把橢球半軸長度按照比例放大,放大比例可以根據實際情況而定。針對某一個點的和針對連續多個點的誤差橢球可視化圖形如圖2和圖3所示。

圖2 單點誤差橢球

圖3 連續誤差橢球
四、應用實例
目前,MWD隨鉆測量工具在鉆井中的普遍使用,基于ISCWSA模型的井眼軌跡不確定性誤差橢球計算和三維可視化對現場鉆井施工有著很好的指導作用。例如:為了防止正鉆井與鄰井相碰,鉆井人員可以通過觀察鉆頭所在位置的誤差范圍是否與鄰井交碰來調整鉆進方向;在打救援井時為了盡量讓其與事故井相碰,鉆井人員可以通過井眼軌跡控制來使誤差橢球中心靠近事故井,從而最大概率的使救援井與事故井相碰。
為驗證實現方法的可行性,選擇渤海某平臺上的兩口相鄰的井B1井和B2井來繪制誤差橢球,用來驗證三維誤差橢球可視化在防碰預測和井眼軌跡控制領域的指導意義,兩口井的井口間距為25 m,各種計算參數選取文獻[4]中提供的參數,井眼軌跡分段數據及相應誤差分析結果分別如表1和表2所示。
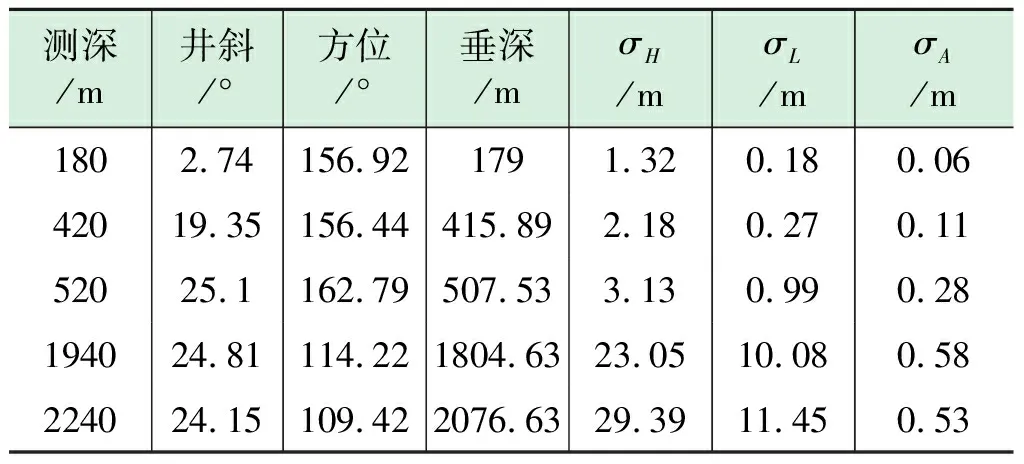
表1 B1井井眼軌跡分段數據及誤差分析結果

表2 B2井井眼軌跡分段數據及誤差分析結果
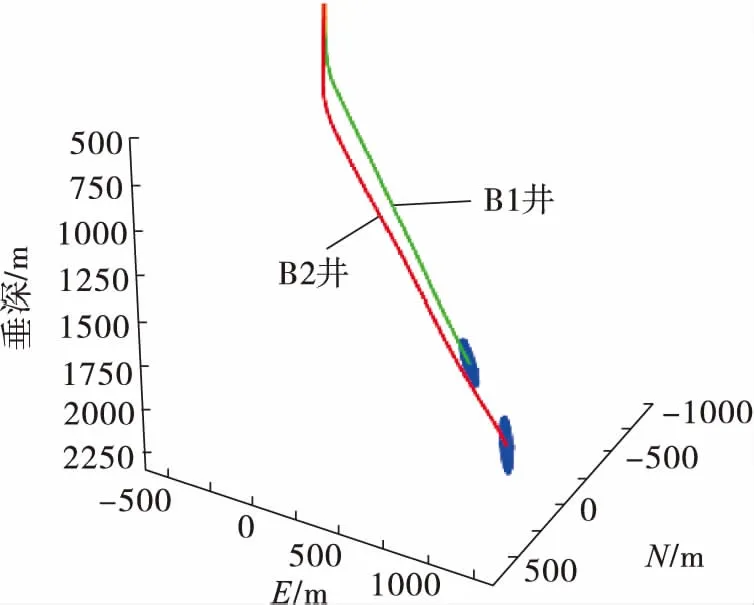
圖4 兩口井防碰預警或連通示例圖
如圖4所示,將B2井作為參考井,B1井在鉆井過程中,在約2 600 m處誤差橢球即將與B2井相碰,若B1井繼續按照原來的方向鉆進,則與B2井碰撞的概率增大,為防止兩井相碰,應及時調整B1井井斜或方位來調整其鉆進方向。
五、結束語
該研究用Python編程語言實現了井眼軌跡的三維可視化和基于ISCWSA法誤差橢球的計算,并展示了隨井深變化的參數信息,取得了良好的效果。在此基礎上,利用NumPy, SciPy, Matplotlib,和Axes 3D等函數庫實現了對三維空間井眼軌跡誤差橢球的可視化,可以直觀的顯示井眼軌跡上各個測點的誤差范圍,對叢式井井眼防碰或井眼軌跡控制領域起到了較好的參考和指導意義。

