Threshold Dynamics of Discrete HIV Virus Model with Therapy
MA Xia(馬霞),CAO Hui(曹慧)
( 1.Department of Science,Taiyuan Institute of Technology,Taiyuan 030008,China;2.College of Science,Shaanxi University of Science and Technology,Xi’an 710021,China)
Abstract:In the paper,we mainly investigate the permanence and the global stability of the discrete HIV model with therapy.By defining the basic reproduction number R0,we conclude the uninfected state P0 is globally stable when R0 < 1,therefore the virus will be extinct.However,the virus will be persistent when R0 > 1.we also obtain the infected state P?is globally stable when 1 < R0 < N by constructing Lyapunov function.The threshold dynamical behavior is in agreement with the continuous differential model.
Key words:Discrete HIV virus model; Basic reproduction number; Persistent; Globally asymptotically stability; Lyapunov function
1.Introduction
AIDS is a serious and deadly disease which is caused by human immunodeficiency virus.HIV-1 is a kind of virus that attacks body’s immune system,and it puts the most important T cells in the body’s immune system as a target,swallows and disrupts large number of T cells,which suppresses the immune system and has strong variability.It means that the virus can reduce the body’s resistance to various diseases.HIV has received widely attention because of its high fatality speed all over the world[1].HIV continues to spread at alarming rates in many places of the world.By the end of 2009,it was estimated that 740,000(560,000~920,000)people were living with HIV/AIDS (PLHIV)in China,of whom 105,000 (97,000~112,000)were living with AIDS.The introduction of HAART has improved the quality of life and morbidity and slowed down the disease progression of HIV-1 infected patients.The HAART treatment reduces the amount of virus in the body of a patient to a very low level,allowing the immune system to recover its strength[2?3].
The HIV dynamics model can describe the relationship between T cells and virus according to the characteristics of virus and its spread in the population.Many drugs are clinically used to control the epidemic spread of HIV.Perelson and Nelson[4?5]formulated a HIV model including HIV reverse transcriptase inhibitors to describe the spread of virus.As we know if virus particles in the blood and healthy CD4+T cells combined together,this will make the concentration of the virus particles decrease.Perelson and Nelson ignored the phenomenon.De Leenheer and Smith[6]supposed (1?η)βTVis the decreased concentration of the virus particles once it enters the target cell and constructed a virus model reflecting the interaction between healthy CD4+T cells and virus particles in the following form
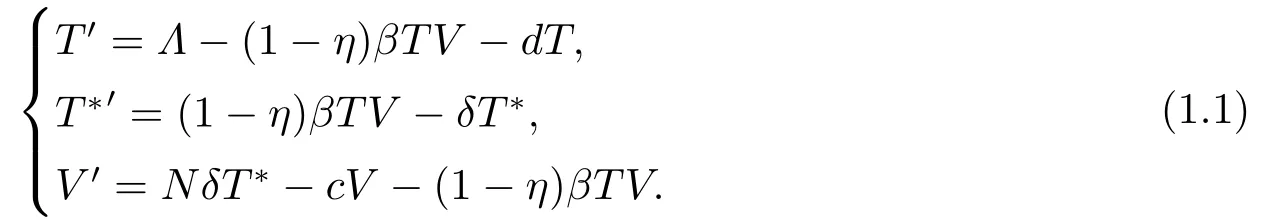
Here,T,T?represent the number of uninfected and infected CD4+T cells at timet,respectively.Vrepresents the concentration of virus particles at timet.All parametersΛ,d,β,δ,N,care given explicit epidemiological interpretations in[4?6].Here,Nis typically large,asN >1.Parameters 0< η <1 is the effectiveness of highly active antiretroviral therapy.Since the infection of virus particles,the death rate of infected CD4+T cells is lager than the uninfected CD4+T cells,namelyd ≤δ.De Leenheer and Smith[6]gave a comprehensive analysis to model(1.1),and proved that the uninfected equilibrium is globally stable and the virus is cleared ifR0<1,and the infected equilibrium is globally asymptotically stable ifR0>1 under certain conditions.
Though the continuous HIV-1 epidemic models have been discussed extensively[7].However,a discrete virus model may be better when we understand more realistic phenomenon for virus transmission and infection[8].Some discrete epidemic dynamical models have also been established to describe the HIV infection[9?14].Since different method of discretizing the continuous model leads to the different discrete model.On the basis of (1.1),we will discrete the above model by the implicit Euler method and analyze the dynamic behaviors,the corresponding discrete model is as follows
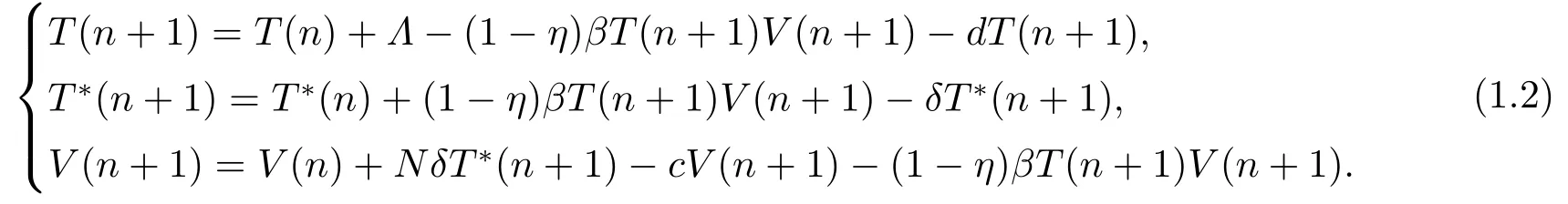
In the following section,we will prove some properties such as positivity and boundedness of the model.In Section 3 we study the extinction and the uniform persistence of virus.In Section 4 we obtain a sufficient condition of the global stability of the infected equilibrium.In Section 5 we make numerical simulations to demonstrate our theoretical result.In the last section,we give the discussion.
2.Boundedness and Positive Invariance
Theorem 2.1Every solution of (1.2)with nonnegative initial values is positive and ultimately bounded for all parametern>0.
ProofThe equations of (1.2)are equivalent to
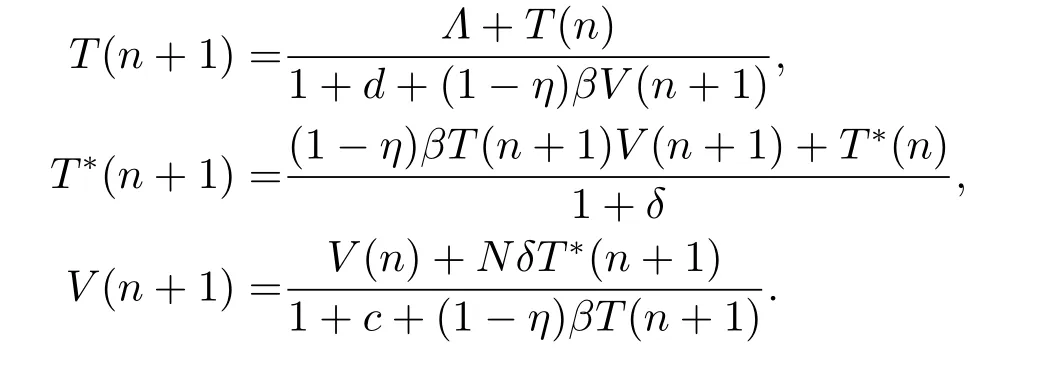
Hence,
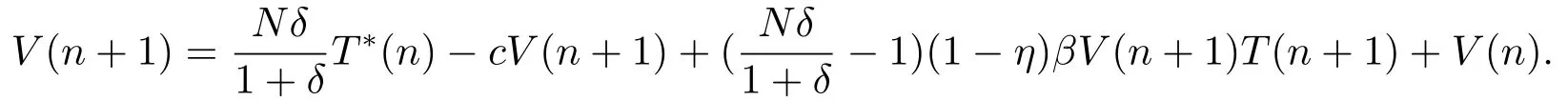
Therefore,we can obtain
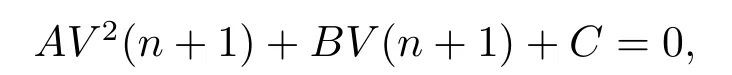
whereA=β(1+c)(1?η),B=(1+d)(1+c)?β(1?η)(V(n)+SinceT(0)>0,T?(0)>0,V(0)>0,we can getC <0 andA>0.Therefore,the quadratic equationAV2(n+1)+BV(n+1)+C=0 have only one positive rootV(1)>0.From the above equation,we haveT(1)>0,T?(1)>0.A similar argument impliesT(2)>0,T(2)>0,V(2)>0.So we can concludeT(n)>0,T?(n)>0,V(n)>0 for alln>0 by mathematical induction.
From the first equation of system (1.2),we have
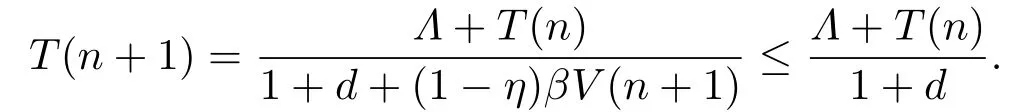
The equationT1(n+1)=has a unique equilibriumwhich is globally asymptotically stable,namelyThe comparison principle[15]implies thatT(n)≤T1(n)≤whenT(0)≤T1(0)≤Hence,
Furthermore,adding the first two equations of system (1.2),we obtainT(n+1)+T?(n+1)=T(n)+T?(n)+Λ?dT(n+1)?δT?(n+1)≤whereω=max {d,δ}.By the similar argument ,we can obtainSoT,T?are bounded.IfT?is bounded,we can obtain thatVis bounded.it follows that there existt >0,MT >0 andMV >0 such that≤Thus the solutions are positive and bounded.
3.Extinction and Permanence of Virus
We define a basic reproduction numberR0which represents the number of infected CD4+T cells produced by a single infected CD4+T cell in a healthy individual when all cells are almost the healthy cells.A single productively infected cell in an otherwise healthy individual with normal target cell level isT=The infected cell producesNvirions,each with life spanwhich will infecthealthy target cells,a viral particle enters a target cell which will lead to the decreased concentration of the virus particles.The basic reproduction number can be deduced toR0=by the idea of[16-17],which reflecting the loss of the original productively infected cell.Clearly,is an state of (1.2)and it exists for all feasible parameter values.The stability of the uninfected stateP0is given in the following theorem.
Theorem 3.1The uninfected stateP0of model (1.2)is globally stable ifR0<1,andP0lose its stability ifR0>1.
ProofFrom the model (1.2),we can have
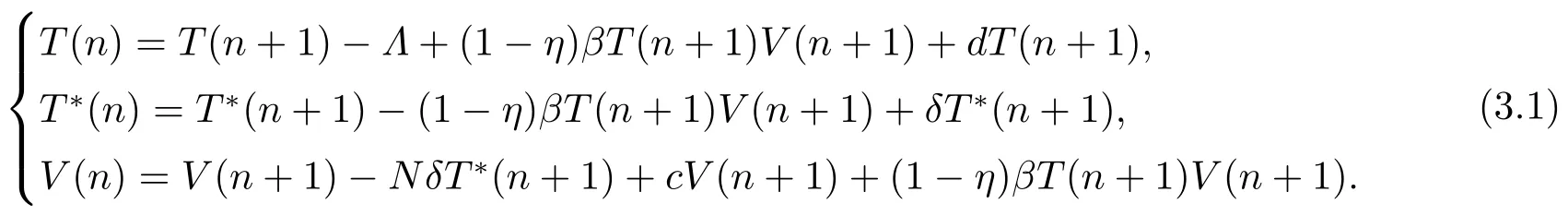
The linearized matrix of model (3.1)at the uninfected stateP0is
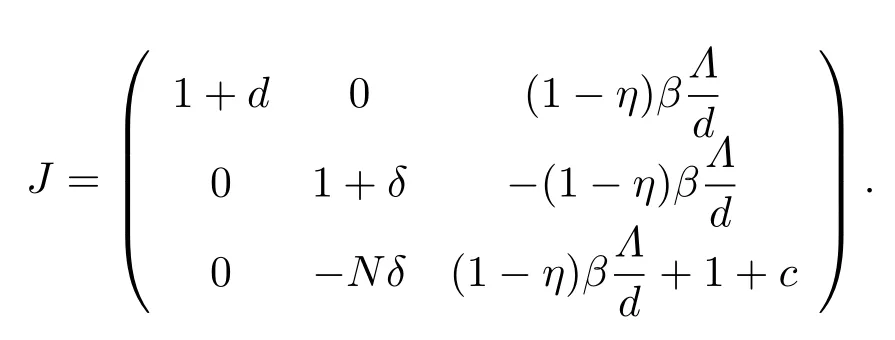
IfR0<1,the eigenvalues of matrixJare lager than 1 through straightforward calculations.Hence,the eigenvalues of matrixJ?1are less than 1.From the Jury criterion[15],we can conclude that the uninfected stateP0is locally stable ifR0<1.
Suppose Lyapunov functionW(n)=NT?(n)+V(n),we have
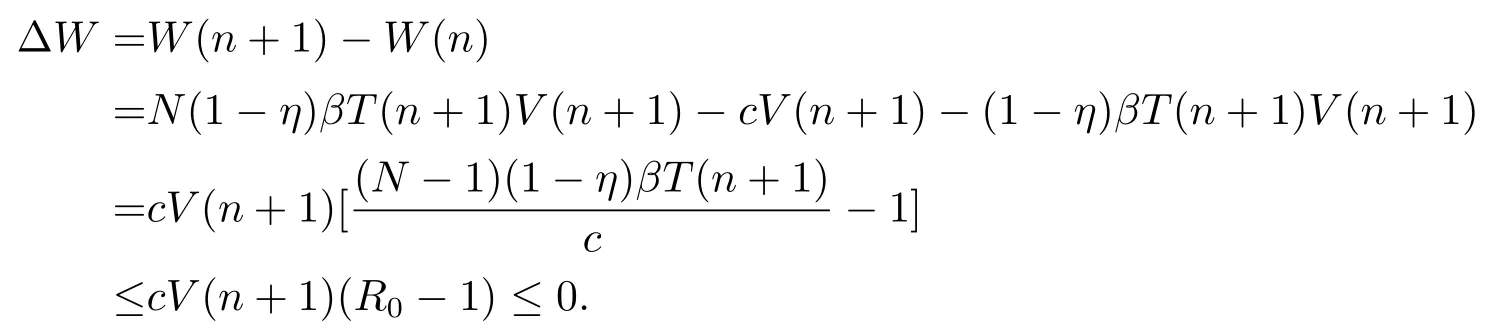
From the hypothesis ofR0<1,we have ?W ≤0.?W=0 if and only ifT?(n)=V(n)=0.The LaSalle’s invariance principle[15]implies thatP0is globally stable.Furthermore,the virus is extinct.IfR0>1,in addition toT?=V=0,whenTis approximate to,?W >0.Hence,apart fromT?=V=0,the solutions starting from the point near toP0are far fromP0.This implies thatP0is unstable whenR0>1.
Theorem 3.2IfR0>1 ,then the virus will keep persistent.
ProofSincethen we have
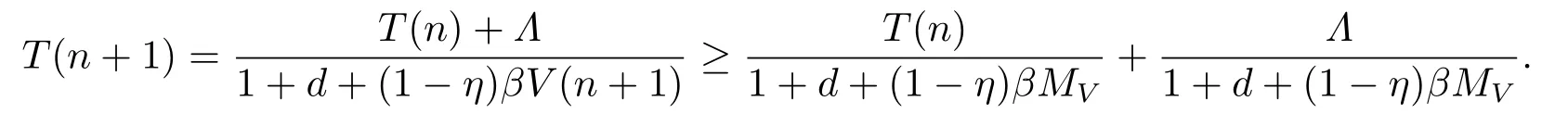
The comparison principle implies
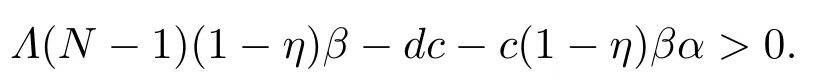
For enough small numberα,we can prove there doesn’t existT1∈N such thatV(n)≤αwhenn>T1.If the conclusion does not hold,from the first equation of (1.2),forn>T1,we have
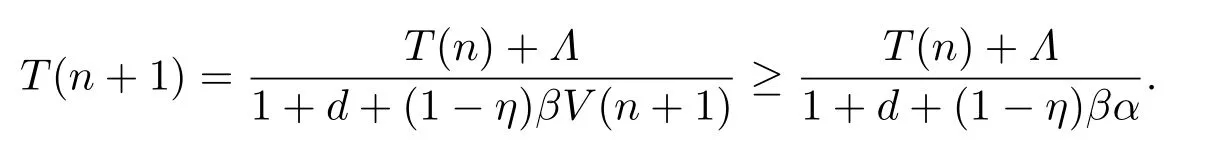
DefineM=Λ(N?1)(1?η)β?dc?c(1?η)βα.Therefore,for any smallε >0(ε
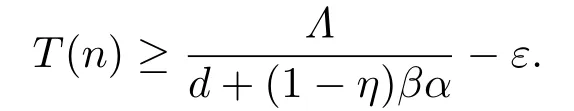
We construct Lynapunov function
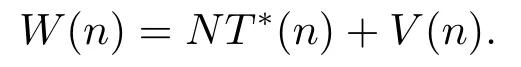
For anyn>T2,we have

Consequently,we haveW(n)→∞asn→∞.ButW(n)is bounded by upper boundedness ofT?(n)andV(n).This is a contradiction.Therefore,our conclusion is true.
Now we only need to investigate two following cases.IfV(n)≥αfor alln,similarly,we have
Otherwise,V(n)oscillates aroundαfor all parametern.We only need to prove there exists a positivemVsuch thatV(n)≥mVifnis enough large.
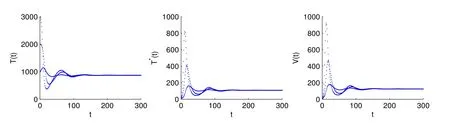
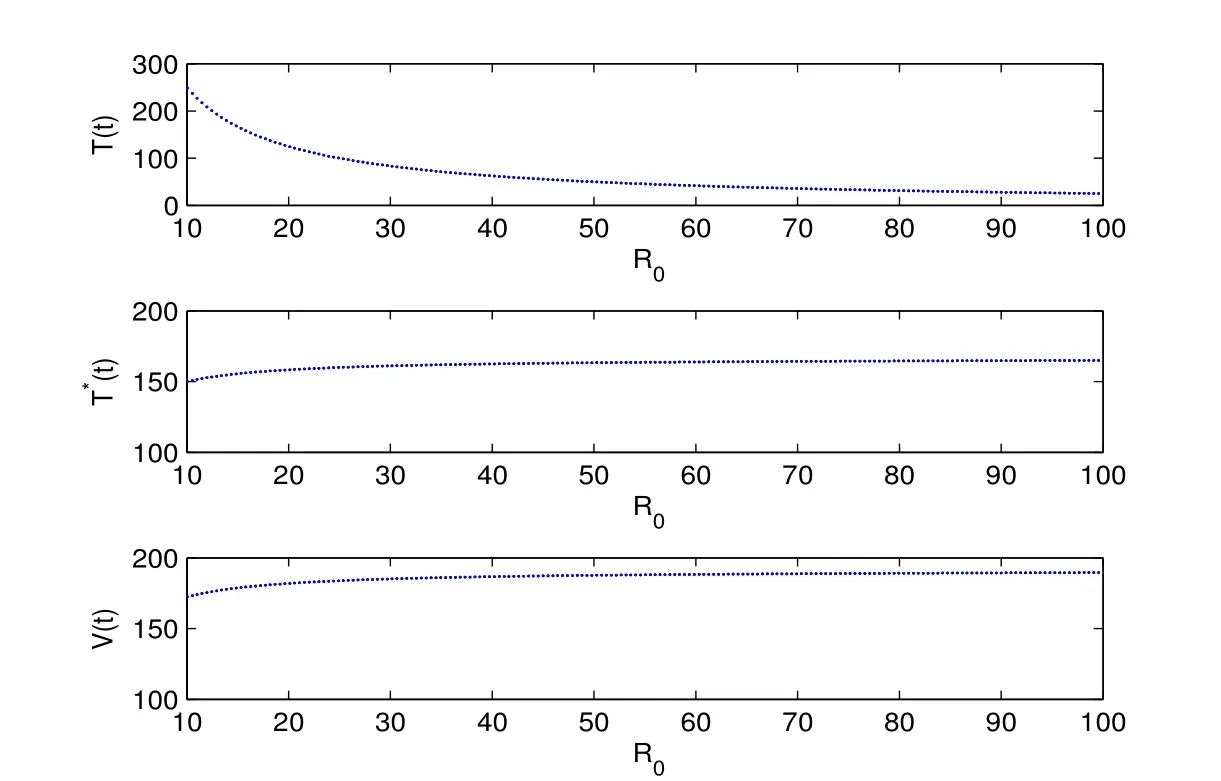
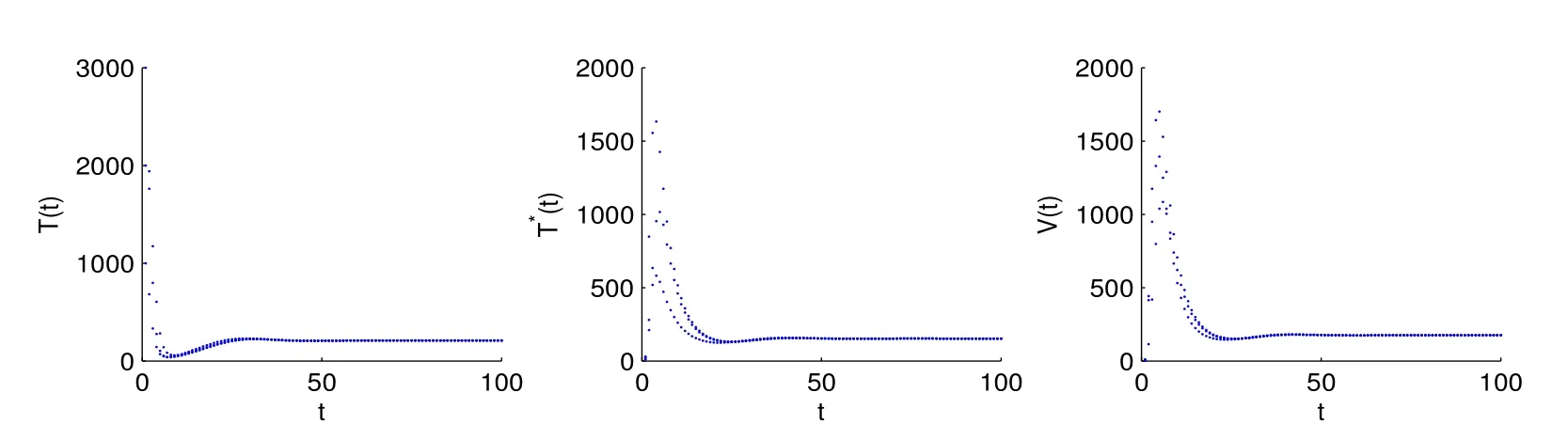
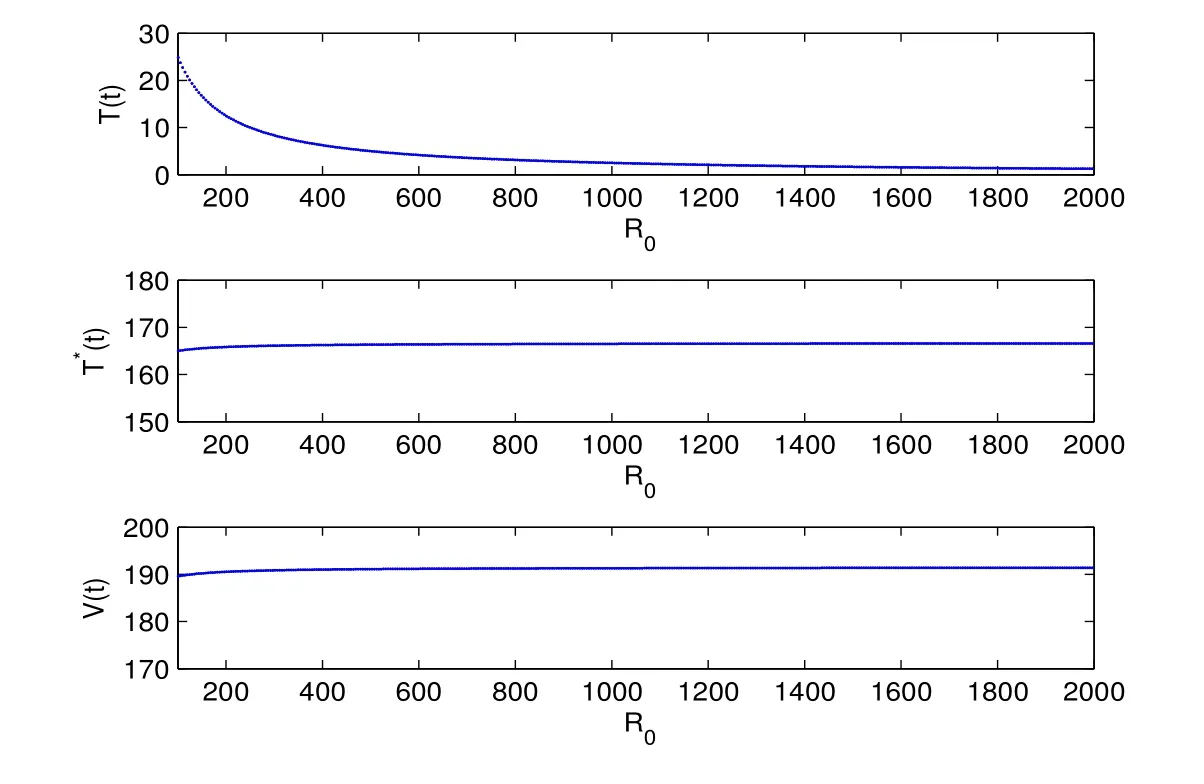
SinceV(n)oscillates aroundαfor alln,we can suppose there are two numbersT3,T4(T4>T3+1)sufficiently large such thatV(T3)≥αandV(T4)≥α,but for anyT3 andW(T3+1)≥Hence ?W(T3+1)>0,and IfT3+2=T4,we obtain IfT3+2 SinceW(n)≥forT3< n < T4still holds ifV(n)≥α,we can conclude that ifnis sufficiently large ,W(n)≥ From the second equation of (1.2),we have The comparison theory[15]impliesTherefore,the virus will keep persistent. By calculations,we can obtain (4.1)only have one infected state whenR0>1 with In the following theorem ,we construct an appropriate Lyapunov function to establish the global stability ofP?. Theorem 4.1Assume that 1 ProofTo the convenience,we introduce identity transformationHence,from (1.2)and (4.1),we can obtain We construct the Lyapunov function as whereF(x)=x?1?lnx.Whenx>0,F(x)≥0,that is,lnx ≤x?1.Then the difference ofW1along a solution of the model (1.2)is ?W1(n)=W1(n+1)?W1(n) From the equations (4.2),we can conclude A similar argument implies that Therefore, Since the arithmetic mean is greater than the geometric mean,2(n+1)?andare negative for all When 1 Hence,?W1≤0.?W1=0 if and only ifT(n+1)=that is, From the equations of the model(1.2),we can getV(n+1)=Using the relation of(Λ?(1+d)T(n+1)+T(n))=Λ?d=(1?η),we can deduce thatThe maximum invariant set is the singletonP?.The LaSalle’s invariance principle[15]implies that the infected stateP?is globally asymptotically stable.Further,virus of model will not eliminate. With parameter valuesΛ=50,β=0.0002,d=0.02,η=0.5 ,δ=0.3,N=10,c=2.35,thenR0=0.96<1,andP0=(2500,0,0).We choose three different initial values to do numerical simulation.The simulation results show that the virus will be eliminated(see Fig.5.1).We choose the similar parameter and make simulations to show the persistence of virus.Here we letβ=0.0006,then 1 Fig.5.1 When R0=0.96,the solutions curve of the model (1.2) Fig.5.2 When R0=2.8723,the solutions curve of the model (1.2) Fig.5.3 When 10 Fig.5.4 When R0=11.9681,the solution curve of the model (1.2) If we vary the value ofβ,whenβ ∈(0.0021,0.021),the straightforward calculation shows that 10 Fig.5.5 When 100 In this paper,we formulate and investigate a discrete HIV-1 virus model.Our results are as follows.We obtain the similar crucial valueR0=IfR0<1,the uninfected stateP0is globally stable,and virus is eliminate.IfR0>1,the system (1.2)is persistent.The infected stateP?is globally asymptotically stable when 1< R0< N.WhenR0> N,the simulation results indicate all solutions converge toP?and no oscillations occur. If we don’t consider that the healthy CD4+T cells and virus particles combined together into the infected CD4+T cells which make the concentration of the virus particles decrease,the threshold parameter yieldswhich is the basic reproduction numberR0calculated in [1-2].The authors concluded that ifR0<1,the only uninfected steady state is globally asymptotically stable,while ifR0>1,in addition to the uninfected equilibrium which is unstable,there is an infected equilibrium which is globally stable. To investigate effect of antiviral therapy,finding the partial derivative ofR0with respect toηgivesR0decreases with increasing treatment uptake,which means that antiviral therapy is beneficial to HIV infection control.Hence,we can decrease the value ofR0by improving the effectiveness of highly active antiretroviral therapy,and control the infection of virus.If the effectiveness of highly active antiretroviral therapy is periodic,the model will present periodic solutions and exhibit much more complicated dynamical behaviors,such as bifurcations and chaos.Our paper mainly focuses on the qualitative theory of equilibrium point and assumes that the parameters are constant.Hence,we do not consider these problems,but which will formulate our further work.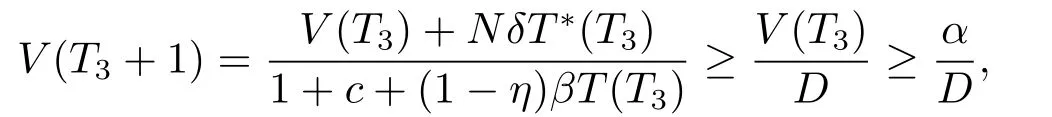
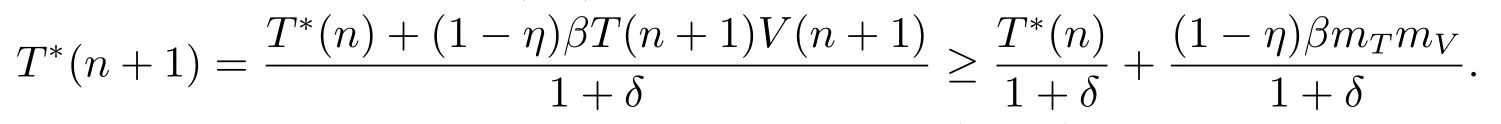
4.Stability of Infected State
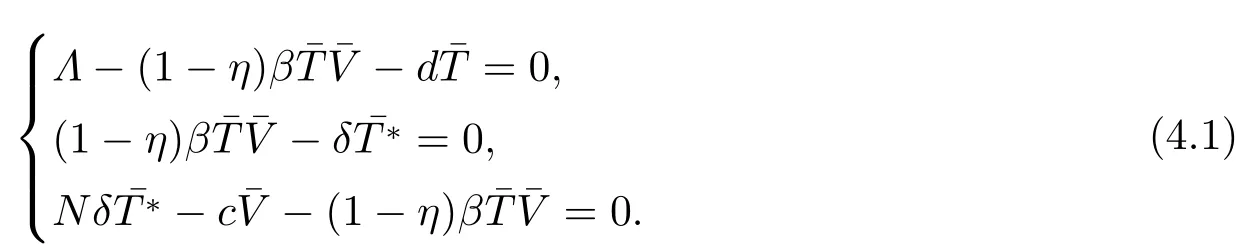
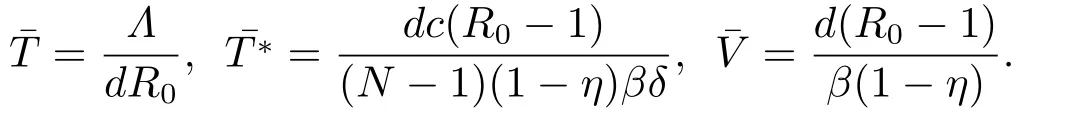
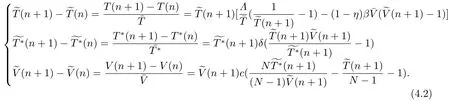
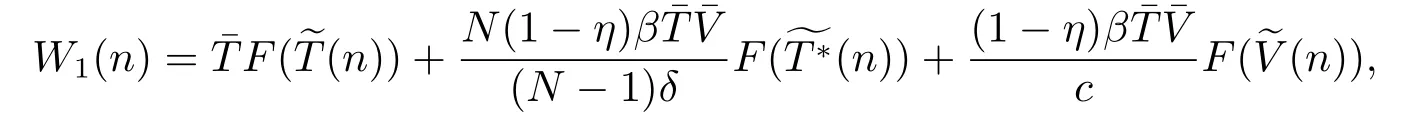
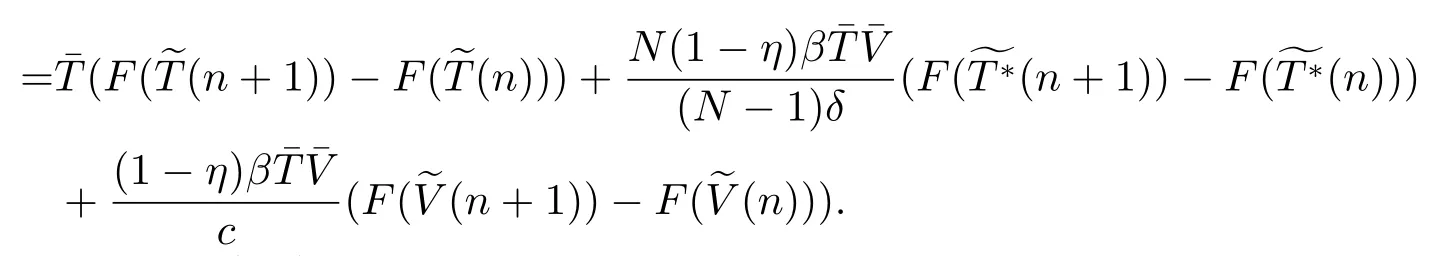


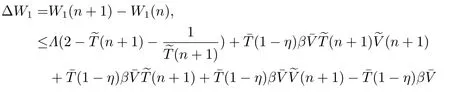
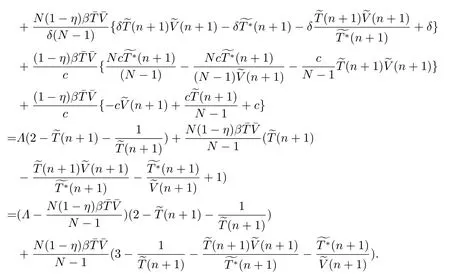
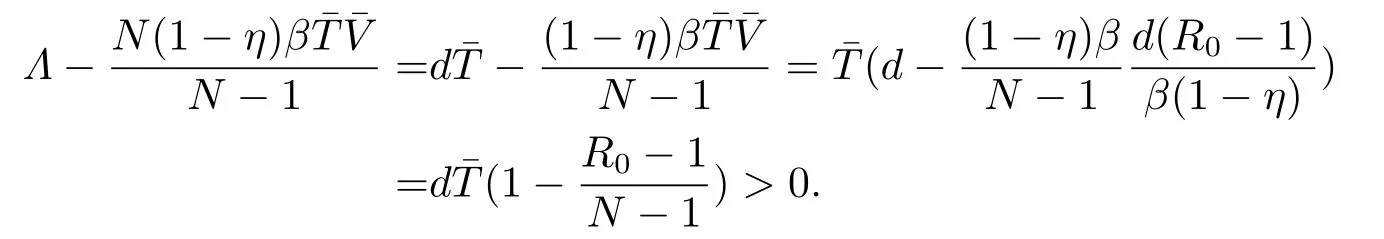
5.Simulation

6.Discussion

