基于乘波前體的2元TBCC變幾何進氣道一體化設計

俞宗漢，謝業平，黃國平，蒲永彬，李 乾，王瑞琳

（1.南京航空航天大學能源與動力學院，南京210016；2.中國航發沈陽發動機研究所，沈陽110015）

0 引言

隨著世界航天領域的軍事競爭日益激烈，對飛行器裝備的要求也不斷提高。結合各類發動機在不同飛行條件下具有的優勢，組合式動力推進系統（如TBCC、RBCC）的概念被提出，該動力系統能夠使飛行器實現從地面起飛到高速巡航的動力銜接[1]。其中，基于TBCC組合動力系統具有單位比沖大、經濟性好、可循環使用等特點，成為航空領域重點發展方向[2-6]。

變幾何進氣道的設計方法是實現TBCC寬馬赫數飛行的關鍵技術之一[7]。通過對進氣道前體的波系和通道內分流板角度的調整，實現飛行包線內各狀態下的最優氣動性能。與3維內轉式進氣道相比，2元進氣道的內部構型和調節機理簡單，其通道密封性更易保證，是實現變幾何進氣道設計的可靠途徑，受到國內外學者的重視。文獻[8-11]針對ATREX 2元進氣道，通過調節壓縮楔板來實現進氣流量和波系的調整，具有流動特征簡單、變幾何調節難度低的特點，但該進氣道第2級斜板的調節會對喉道面積產生明顯影響，從而限制了變幾何調節裕度；文獻[12-13]針對X-43B進氣道，通過增加調節自由度來提升其內流性能，使飛行器在馬赫數為4.0~7.0下具有較好的性能；文獻[14-15]針對內并聯式TBCC動力方案，通過調節TBCC內部的分流板改變在不同工作狀態下各通道的流量，完成在2.0~5.0倍聲速飛行條件下的模態轉換；文獻[16]提出1種2元內并聯式TBCC進氣道結構，在大部分工況下總體性能較好，并且流場質量和出口參數也表現良好；文獻[17]提出1種內并聯式TBCC方案，分析了變幾何泄流腔及其設計參數對進氣道內部流場特性的影響。綜合以上2元TBCC變幾何進氣道的研究可知，其內外流場以及內并聯TBCC的2個流道的流場具有高度耦合的特性，是TBCC飛發一體化設計需解決的主要問題之一。總偏轉角和進氣道外唇口角度是2元混壓式進氣道的2個關鍵參數。總偏轉角影響進氣道內外壓縮段的壓縮效率，從而影響進氣道的低馬赫數起動性能；而唇口角影響飛行器的整體力矩平衡和所受外部阻力。

本文基于1種推進系統綜合推阻性能分析方法，設計了1種2元混壓式TBCC進氣道，并對馬赫數為2.0~4.0的單通道性能進行計算分析；并對過渡模態下的雙通道模型進行氣動計算，分析了不同開度下的進氣道性能變化。

1 2元進氣道及其變幾何方案設計

1.1 進氣道氣動構型

2元混壓式TBCC進氣道外壓縮段由按等波強原理配置的3級斜激波組成。設計飛行高度為24 km，設計馬赫數為 4，其他馬赫數（Ma=3.5、3.0、2.5、2.0）的飛行條件根據等動載原則得到。結合基于多級錐導乘波體設計的前體型面，利用高速巡航飛行器綜合推阻分析方法（如圖1所示）[18]，得到最佳的2元進氣道幾何參數（總偏轉角為23°，唇口角度為10°），設計了2元混壓式進氣道的氣動構型，如圖2所示。

1.2 進氣道數值模擬

本文對設計的前體/進氣道氣動造型進行結構化網格劃分與邊界條件設置，如圖3所示。近壁面的y+=30，第1層網格約為0.1 mm，網格總數約為300萬。

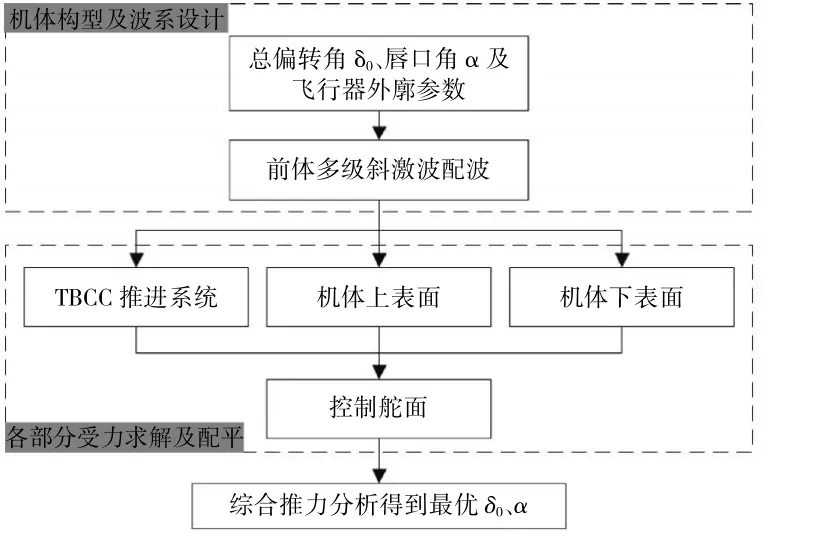
圖1 推進系統綜合推阻分析方法

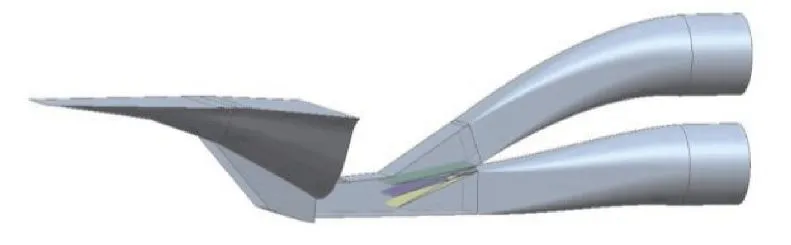
圖2 一體化2元TBCC變幾何進氣道完整造型

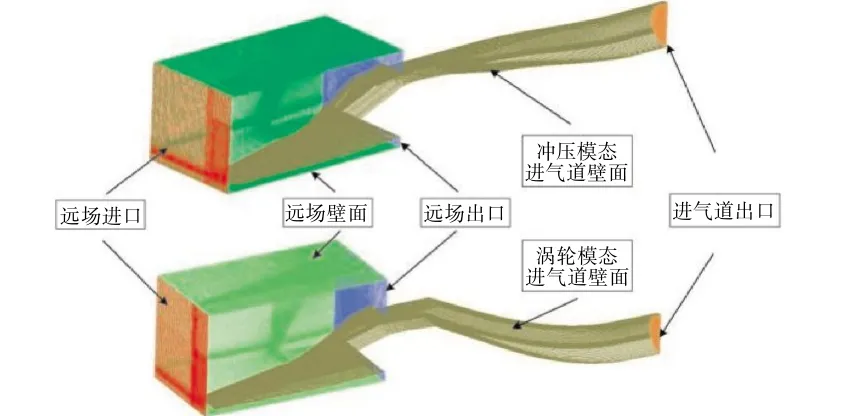
圖3 帶前體的2元TBCC進氣道網格拓撲結構

采用商業軟件CFX進行數值模擬。采用標準ke湍流模型、標準壁面函數，其校驗應用與文獻[19]中相同的造型。沿程壓力結果分析如圖4所示。從圖中可見，數值仿真結果與試驗結果吻合度較高，所以標準k-e湍流模型可以用于本文2元TBCC進氣道的模擬驗證。

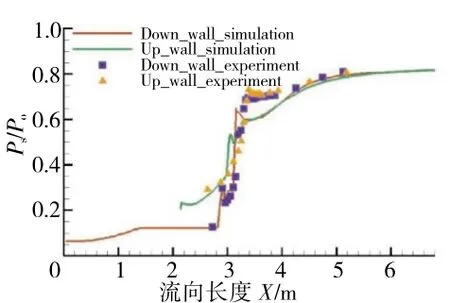
圖4 沿程壓力分布CFD結果與試驗結果的對比

2 進氣道模態轉換變幾何調節規律

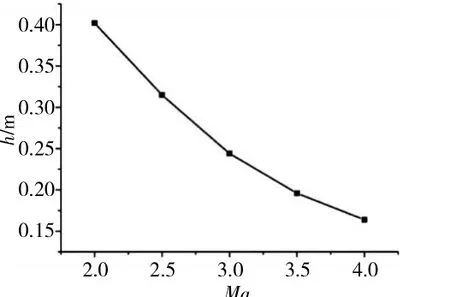
圖5 基于進氣道喉道高度h與馬赫數Ma的變幾何結構調節規律

進氣道喉道高度h隨飛行速度變化的調節規律如圖5所示。當飛行馬赫數低于轉級馬赫數時，TBCC處于渦噴工作模態，所有流量都流入渦輪通道；當飛行馬赫數高于轉級馬赫數時，TBCC處于過渡態模態，氣流分別流向渦輪流路和沖壓流路，通過調節分流板來改變2路的流量比，從而實現模態轉換。本文選擇的轉級馬赫數為2.5，即在馬赫數為0~2.5時，進氣道為渦輪工作模態；在馬赫數為2.5~4.0時，進氣道為沖壓工作模態；在馬赫數為2.5時，完成模態轉換。對應的變幾何機構包括轉動壓縮板、轉動伸縮板、弧形轉動板、圓弧滑動板和喉道水平板。當飛行狀態變化時，通過調節可調機構改變喉道面積，從而滿足飛行狀態的改變，確保進氣道具有最好的性能。

3 單通道性能分析

馬赫數為2.0~4.0時進氣道典型飛行狀態數值仿真結果如圖6所示。從圖中可見，在設計狀態馬赫數為4.0時，3道入射激波與設計相符，貼口狀態均較好，僅有少量溢流，流量捕獲性能較高。馬赫數為3.5、3.0時，來流速度減小，激波脫離唇口向外側移動，可見唇口的溢流隨馬赫數的降低而逐漸增加。當來流速度處于轉級馬赫數2.5時，2個通道同時工作，雖然溢流量比馬赫數為3.0時的增大，但是由于雙通道以及喉道的放大保證了進氣道的通流能力，所以溢流的增加比例小于沖壓工作模態時馬赫數減小的溢流變化比例。當馬赫數為2.0左右時，TBCC進入渦輪工作模態，流量捕獲能力相對降低，由于進氣道激波強度的減小，進氣道的總壓損失也相應減小。

圖6 各來流馬赫數下對稱面的速度及總壓恢復系數

進氣道的各項氣動性能隨馬赫數的分布如圖7所示。從圖中可見，在沖壓工作模態下，隨著飛行馬赫數的提高，進氣道入射激波的強度增加，進氣道唇口溢流量減小，所以流量系數增大，壓比增大，出口馬赫數降低，總壓損失增大。當進氣道來流馬赫數達到4.0時，其對應流量系數為0.92，此時沖壓通道出口馬赫數達到0.27時，可以滿足該通路的來流氣體進口速度要求，且在進氣道出口的平均總壓恢復系數為0.47。當馬赫數高于2.5時，進氣道為渦輪工作模態，最大流量系數可達0.65；由于進氣道入射激波的強度降低，所以相對于沖壓工作模態，渦輪通道出口截面的平均總壓恢復系數大于0.75。總之，數值模擬結果表明：在工作馬赫數為2.0～4.0時，變幾何進氣道均能成功起動，流量系數在0.60以上，進氣道總壓恢復系數為0.47～0.85，氣動性能良好。

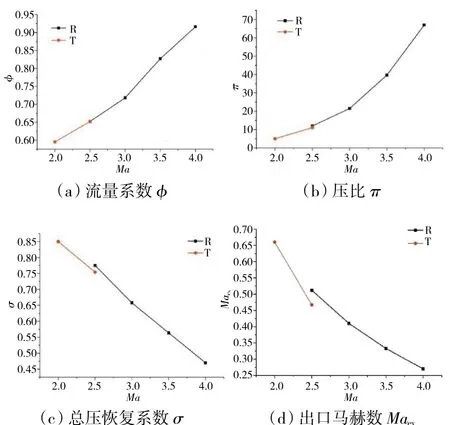
圖7 進氣道各性能隨馬赫數的分布

4 雙通道性能分析

對于過渡模態下的氣動分析，選擇3個不同的分流板位置，形成3個定幾何構型，并對雙通道模型進行結構性網格劃分（如圖8所示），對壁面網格加密，邊界層高度為0.1 mm，以保證y+≈30，網格總量為350萬。選用標準k-e湍流模型和標準壁面函數進行計算。

3個不同開度下通流狀態的流場結構如圖9所示。在開度為1時，渦輪通道流量約為沖壓通道流量的30%，分流段前氣流的最大速度為馬赫數1.6，經過分流段后，沖壓通道內氣流最大速度為馬赫數2.6，渦輪通道內氣流最大速度為馬赫數3.4；由于分流板的開度不會影響到分流段前的氣流流場分布，因此在開度2和開度3下，分流段前的氣流最大馬赫數約為1.6。此外，在開度2下，沖壓通道與渦輪通道的流量相當，2個通道擴張程度基本一致，因此2個通道內最高馬赫數約為2.7；在開度3下，沖壓通道流量僅為渦輪通道的35%，經過分流段加速后，沖壓通道內最大速度為馬赫數3.3，渦輪通道內最大速度為馬赫數2.3。

若分別在沖壓通道與渦輪通道出口處施加一定的反壓，使得2個通道內的結尾激波運動至分流板前緣位置處（如圖10所示），此時分流段前的氣流仍為超聲速，2個通道之間互不干涉，進氣道性能最佳。

圖9 來流Ma=2.5時不同開度下通流狀態流場結構

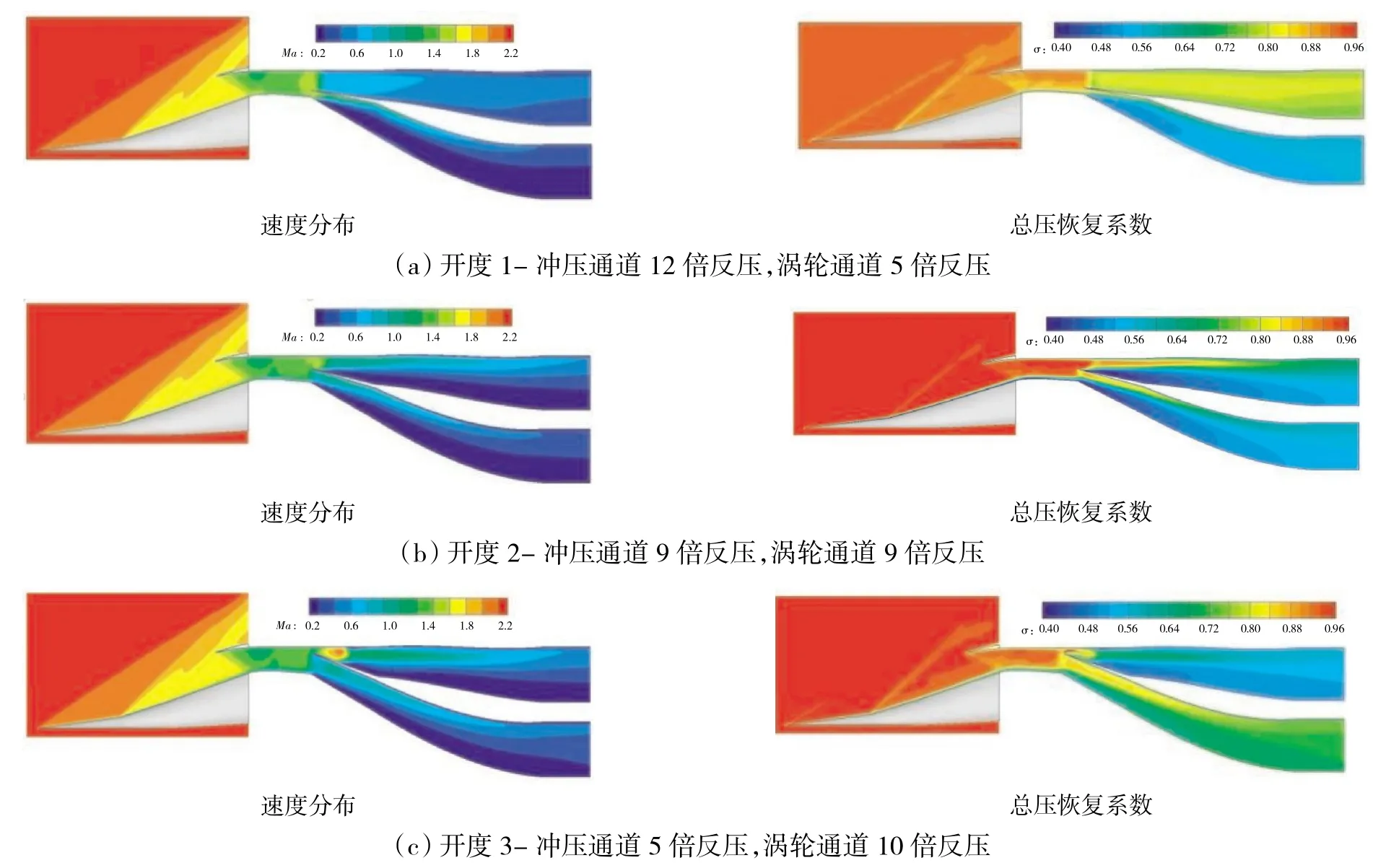
圖10 來流速度為Ma=2.5時不同開度下沖壓和渦輪通道的反壓特性

從圖中可見，在開度1下，當沖壓通道出口反壓為來流壓力的12倍，渦輪通道出口反壓為來流壓力的5倍時，2個通道內的結尾激波運動至分流板前緣，此時沖壓通道出口平均馬赫數為0.333，渦輪通道出口平均馬赫數為0.287；在開度2下，當雙通道出口壓力為來流壓力的9倍時達到此狀態，沖壓通道出口平均馬赫數為0.370，渦輪通道出口平均馬赫數為0.270；在開度3下，在沖壓通道出口施加5倍反壓，渦輪通道出口施加10倍反壓，結尾激波位于各自通道內，未進入擴張段，此時沖壓通道出口平均馬赫數為0.364，渦輪通道出口平均馬赫數為0.362。流量大的通道往往具有承受更大出口反壓的能力。

不同的分流板開度對應著不同的通道流量分配，將沖壓通道流量與渦輪通道流量的比值定義為流量比，得到了不同流量比下2個通道的流量系數與總壓恢復系數的變化規律，如圖11所示。一般情況下，流量較大的通道出口氣動性能參數優越，性能更好。總體上隨著沖壓通道流量的增加，從流量系數和總壓恢復系數來看，沖壓通道的氣動性能逐漸轉好，而渦輪通道的氣動性能逐漸變差。此外，當沖壓通道流量小于渦輪通道流量時，相較于流量比大于1的情況，沖壓通道的氣動性能對流量變化更為敏感。

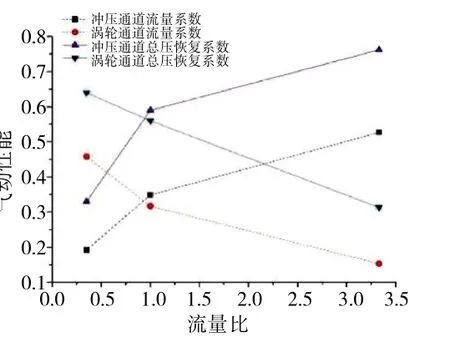
圖11 過渡模態（Ma=2.5）氣動性能隨流量比的變化規律

5 結論

本文設計了1種基于乘波前體的2元TBCC變幾何進氣道，并進行了相關工作狀態的數值模擬與分析計算，得到的主要結論如下：

（1）通過對飛行器受力及總壓損失的綜合推阻分析，得到在最小總壓損失前提下凈推力最大的2元進氣道關鍵參數：總偏轉角δ0=23°及唇口角度α=10°，設計了2元TBCC變幾何進氣道；

（2）對2元TBCC進氣道的數值模擬結果表明，在工作馬赫數為2.0～4.0時，變幾何進氣道均能成功起動，流量系數為0.60以上，進氣道的總壓恢復系數為0.47～0.85，氣動性能良好；

（3）在過渡模態下，針對不同的沖壓通道和渦輪通道的流量分配方案，對雙通道模型進行了計算，總結得到不同的流量分配對2元變幾何進氣道的氣動性能影響規律。

上述結論可有效地為TBCC變幾何方案應用于工程實際提供可靠的參考和依據。