基于數(shù)學(xué)曲線的高速鐵路線下工程沉降預(yù)測分析
包永鋼
(太原市勘察測繪研究院,山西 太原 030001)
1 引 言
為了滿足在高速行駛條件下的安全性,高鐵線路必須有高精度的幾何線性參數(shù),以達(dá)到高平順性。而高速鐵路由于自身調(diào)整能力的限制,對線下工程的沉降變形提出了嚴(yán)格要求。國內(nèi)外高速鐵路成功和失敗的經(jīng)驗教訓(xùn)都告訴我們:工后沉降的控制和預(yù)測是決定高速鐵路客運(yùn)專線建設(shè)成敗的關(guān)鍵因素之一,因為它不僅影響著行車的安全、速度、舒適及人們對高鐵的整體評價,影響高鐵使用性能和運(yùn)輸效益的發(fā)揮,同時也影響車輛的使用壽命,嚴(yán)重的可導(dǎo)致交通事故的發(fā)生。
我國現(xiàn)行各種高速鐵路設(shè)計規(guī)范也只對工后沉降及不均勻沉降的大小做了規(guī)定,還沒有一套比較完整而又實用的監(jiān)測和預(yù)測方法,這就要求我們基于理論,建立起一套適合我國實際的高鐵沉降監(jiān)測方案,進(jìn)而提出工后沉降預(yù)測方法,尋求基礎(chǔ)沉降隨時間的變化規(guī)律,分析影響基礎(chǔ)沉降的主要因素,從而提出減少工后沉降所能采取的工程措施[2]。
2 基于數(shù)學(xué)曲線的沉降預(yù)測模型
目前,關(guān)于沉降分析的數(shù)學(xué)曲線擬合法,是在太沙基等人創(chuàng)立的經(jīng)典土力學(xué)基礎(chǔ)上,引入許多簡化假定,將實測沉降的趨勢看成某種規(guī)律的變化,建立相應(yīng)的模型,采用數(shù)學(xué)方法計算出所需的參數(shù),得出沉降時間的關(guān)系再用于后期沉降預(yù)測[4,5]。基于數(shù)學(xué)曲線的沉降預(yù)測方法都以下式為基礎(chǔ):
St-S0=(S-S0)f(t-t0)
(1)
式中,St:t時刻的沉降量;S0:t0時刻的初始沉降量;S:最終沉降量;t-t0:相對時間;St-S0:t0時刻之后沉降增量;f(t-t0):待定函數(shù)式。在沉降預(yù)測中,S-St常稱為t時刻剩余沉降,或后期沉降。如t0取為完工時刻,St-S0稱為工后沉降量,S-S0稱為最終工后沉降量[4,5,7]。
高速鐵路沉降評估以《客運(yùn)專線鐵路無碴軌道鋪設(shè)條件評估技術(shù)指南》(以下簡稱指南)為技術(shù)依據(jù),指南中共提供了11種沉降評估方法,其中9種為數(shù)據(jù)曲線法,如雙曲線配合法、指數(shù)曲線法、固結(jié)對數(shù)配合法、生長曲線法、Asaoka法等[8,9,11]。各類曲線擬合方程及其優(yōu)缺點如表1所示。

常用的沉降曲線擬合方法 表1

續(xù)表1
注:St:時間t時刻的沉降值,S:最終沉降量,S0:初期沉降量,Sd:瞬時沉降量,t0:初始時間,a,b,c,α,β:曲線參數(shù)。
基于數(shù)學(xué)曲線擬合的沉降預(yù)測方法不能直接考慮荷載變化的影響,而且參數(shù)也沒有具體的物理意義,但求解方法較簡單直觀,應(yīng)用比較普遍。
3 工程實例分析
3.1 高速鐵路沉降特點
高速鐵路主體結(jié)構(gòu)可以是橋涵工程、路基工程等,不同的主體結(jié)構(gòu)施工工藝不同,為了對比每種預(yù)測方法的適用性和準(zhǔn)確性以及變形預(yù)測的效果,采用某高速鐵路一個區(qū)段的實際沉降觀測數(shù)據(jù)進(jìn)行分析。區(qū)段長度為 18 km,其中橋涵工程長 11.6 km,布設(shè)橋梁墩身觀測標(biāo)424個,路基工程長 6.4 km,布設(shè)觀測標(biāo)157個。
高速鐵路線下工程沉降的主要影響因素是地質(zhì)條件和施工工藝。選取區(qū)段中一個典型的路基測點(1 595測點)和一個墩身觀測點(1 174測點)的沉降數(shù)據(jù)作為分析對象。觀測數(shù)據(jù)嚴(yán)格按照作業(yè)規(guī)范觀測,數(shù)據(jù)觀測時間為2017年5月~2018年6月。
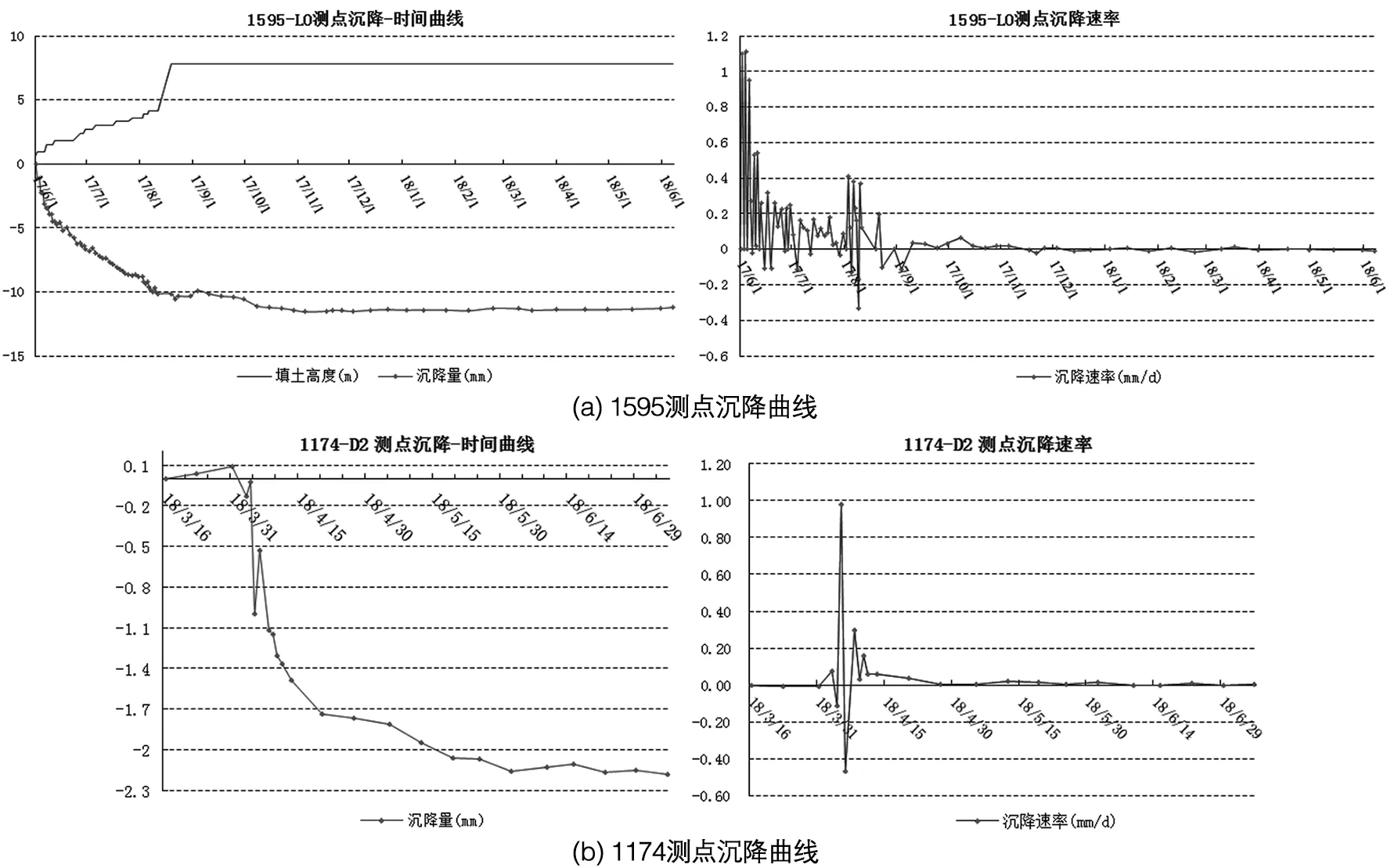
圖1 實測高速鐵路沉降數(shù)據(jù)的沉降曲線
從沉降曲線(如圖1所示)可以看出,路基沉降曲線較為平穩(wěn),在填筑初期的沉降速率波動比較大,后期趨于穩(wěn)定,而墩身沉降只是在架梁期間波動大,沉降曲線呈現(xiàn)明顯的“臺階”現(xiàn)象。這是由于不同的基底處理方法對沉降變形影響不同。在本工程中,路基全部采用CFG管樁處理方式,墩臺全部采用摩擦樁處理方式。沉降量與路基填土高度有密切聯(lián)系,主要沉降發(fā)生在填土過程中,填土高沉降量大,填土低沉降量就小。路基一開始填筑,便發(fā)生較大的瞬時沉降,隨著填土的加大,沉降量也越來越大;當(dāng)填土高度接近設(shè)計高度時,沉降曲線變緩,趨于穩(wěn)定。在兩次填土間隔,即填土?xí)和V校两禃永m(xù)一段時間。這表明沉降量與填土高度之間呈非線性的關(guān)系,其隨著填土高度的增大而增大,而且增加量呈現(xiàn)衰減的趨勢。沉降量與荷載之間有滯后的關(guān)系。
本工程中,路基和橋涵工程沉降絕大多數(shù)都符合此特點,統(tǒng)計發(fā)現(xiàn),絕大部分橋涵實測沉降量小于 5 mm,主要集中在 0 mm~3 mm之間,如表2所示,路基累計沉降量集中在 0 mm~20 mm之內(nèi),如表3所示。而且部分地段展開觀測作業(yè)的時間相對滯后,實測得到的總沉降量較真實值相對偏小。

橋涵累計沉降量統(tǒng)計 表2

路基累計沉降量統(tǒng)計 表3
3.2 不同結(jié)構(gòu)的沉降曲線擬合分析
(1)路基測點分別采用開始觀測到填筑結(jié)束后50天內(nèi)和100天內(nèi)的沉降監(jiān)測數(shù)據(jù);墩身測點分別采用開始觀測到架梁后35天內(nèi)和60天內(nèi)的沉降監(jiān)測數(shù)據(jù),用曲線擬合法預(yù)測。
按照指南規(guī)定,沉降曲線回歸的相關(guān)系數(shù)不得小于0.92[2],因此這里也以相關(guān)系數(shù)γ是否達(dá)到0.92作為評價預(yù)測方法適用性的標(biāo)準(zhǔn)。但為了分析相關(guān)系數(shù)γ的適用性,選取殘差平方和SSE(sum of squares for error)及均方根誤差RMSE(root mean squarederror),預(yù)測采用平均相對誤差絕對值MAPE(mean absolute percent error)作為對比指標(biāo)。這三個精度指標(biāo)的計算方法如下:
殘差平方和:
(2)
均方根誤差:
(3)
平均相對誤差絕對值:
(4)
(2)利用時間平方根法計算測點的近似最終沉降(分別為S(1595)=11.394 mm,S(1174)=2.146 mm),然后采用開始觀測到填筑結(jié)束后一定時期內(nèi)的沉降監(jiān)測數(shù)據(jù),分別采用雙曲線法、Asaoka法和Usher曲線三種較為常用的曲線擬合法對選取的兩個路基測點的觀測數(shù)據(jù)進(jìn)行擬合,并連續(xù)預(yù)測10期數(shù)據(jù);求出預(yù)測的MAPE,并求出最終沉降,與近似最終沉降比較分析,以此來分析各種預(yù)測方法的預(yù)測效果。墩身沉降用曲線擬合做類似的分析。
這三種方法的預(yù)測成果如表4、圖2所示。
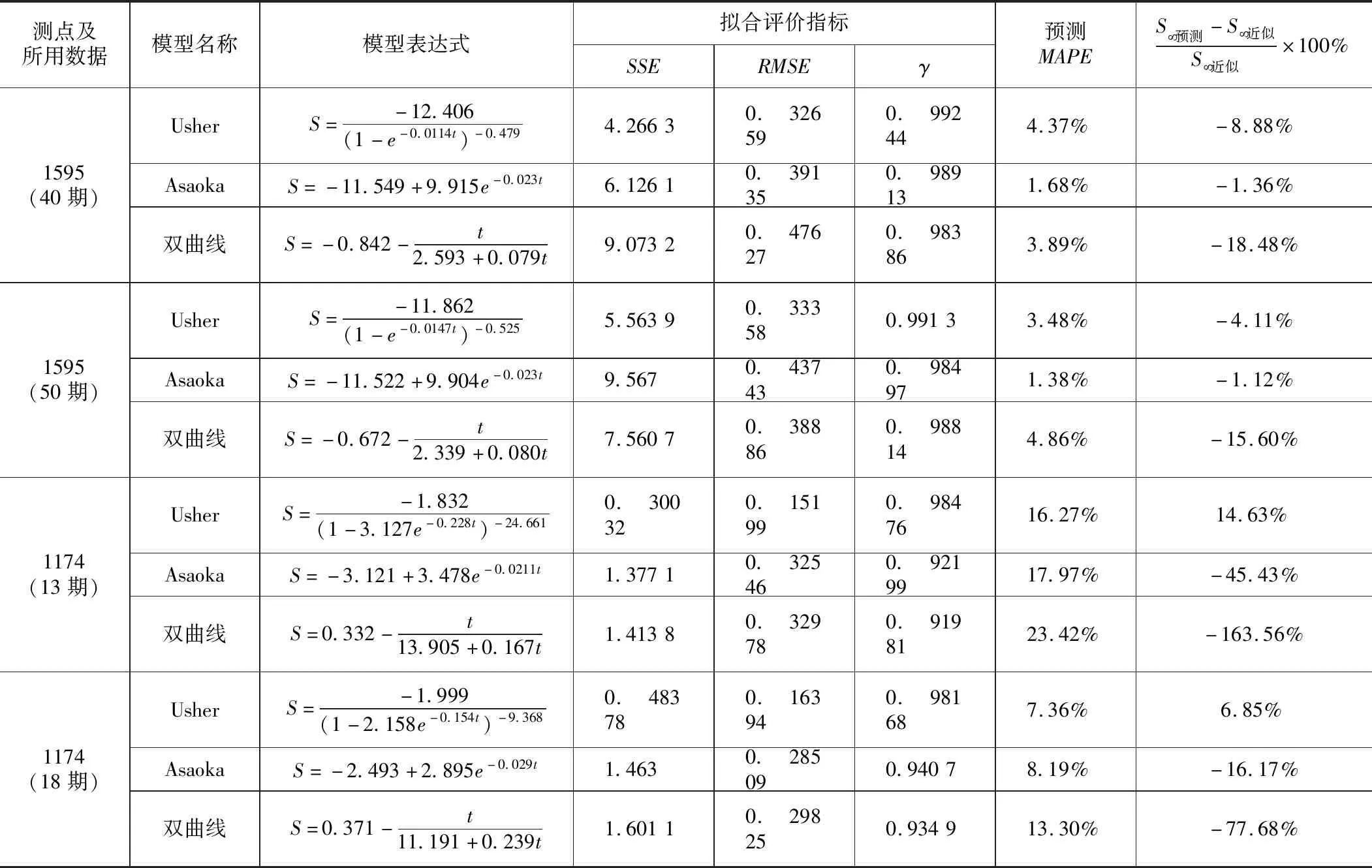
實測數(shù)據(jù)的曲線擬合分析結(jié)果 表4
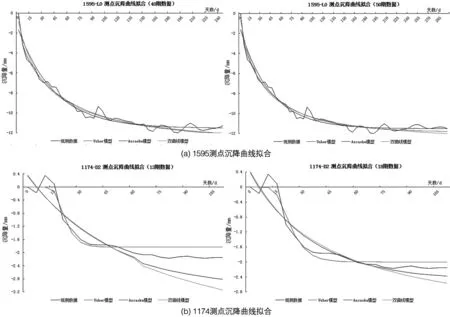
圖2 實測數(shù)據(jù)的沉降曲線擬合分析
3.3 分析結(jié)論
直觀上看曲線擬合預(yù)測路基沉降能夠達(dá)到很好的效果,但是對于墩身的預(yù)測顯得勉強(qiáng)。從表4的擬合評價指標(biāo)可以看出,3個指標(biāo)反映出來曲線的擬合效果是一致的,RMSE和SSE越小,γ越大,擬合效果越好。雖然采用這3種方法進(jìn)行曲線擬合的相關(guān)系數(shù)較高,基本均能達(dá)到0.92以上。但擬合所用數(shù)據(jù)量大小對殘差平方和與相關(guān)系數(shù)有較大的影響,數(shù)據(jù)越少,回歸相關(guān)系數(shù)明顯降低,當(dāng)時間段過短時,甚至導(dǎo)致相關(guān)系數(shù)低于0.92,比如1174測點用13期數(shù)據(jù)擬合,相關(guān)系數(shù)低于0.92;數(shù)據(jù)多時,殘差平方和明顯增大。但是,對比這3個統(tǒng)計指標(biāo),可以看出相關(guān)系數(shù)變化很小,不能反映擬合的優(yōu)劣。這是因為相關(guān)系數(shù)有個明顯的缺點:只能用來比較線性擬合曲線,不能用于評價非線性擬合曲線,它的高低只能反映預(yù)測值與真實值之間是否有良好的線性關(guān)系,并不能說明其值比較相近,在樣本容量n較小時,僅憑相關(guān)系數(shù)較大就判定變量之間有密切的線性關(guān)系是不妥當(dāng)?shù)摹R虼耍脷埐钇椒胶团c均方誤差最小選擇模型的曲線預(yù)測方法得到的沉降預(yù)測值,相比于相關(guān)系數(shù)能更好地評價擬合效果,不同曲線預(yù)測方法的殘差平方和指標(biāo)波動較大,評價得更直觀。
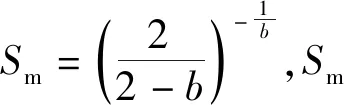
4 結(jié) 語
基于數(shù)學(xué)曲線方法進(jìn)行高速鐵路沉降預(yù)測參數(shù)求解簡單,擬合誤差較小,預(yù)測效果和數(shù)據(jù)量大小有關(guān),具有一定的實用性,能用于類似路基連續(xù)堆載的區(qū)段,在模型應(yīng)用中,用相關(guān)系數(shù)評價擬合和預(yù)測的效果優(yōu)劣是不明顯的,采用SSE和RMSE作為評價擬合效果是比較明顯,因此實際沉降預(yù)測中可以將三個指標(biāo)結(jié)合進(jìn)行評價。
數(shù)學(xué)曲線擬合方法對于墩身的擬合和預(yù)測效果明顯差于路基,這是由于墩身在架梁完成后沉降迅速趨于穩(wěn)定,不具有指數(shù)曲線趨勢。現(xiàn)行規(guī)范要求針對橋梁實測數(shù)據(jù)須開展曲線擬合回歸,但墩身沉降“臺階”特性決定了曲線擬合回歸效果不理想,甚至出現(xiàn)無法擬合預(yù)測的情況。《指南》中同時給出了灰色模型和神經(jīng)網(wǎng)絡(luò)預(yù)測模型,經(jīng)計算分析,如果采用灰色模型評價,由于灰色模型本身也具有指數(shù)曲線趨勢,采用神經(jīng)網(wǎng)絡(luò)預(yù)測,存在建模困難、求解的模型參數(shù)不具有普遍性的情況。在本工程實踐中針對橋梁墩身沉降提出了一種簡單實用、便于進(jìn)行編程計算的評估方法:
(1)架梁完工后觀測期不小于3個月,觀測頻次按照規(guī)范執(zhí)行,沉降曲線無異常波動且波動幅度在 3.0 mm之內(nèi)、沉降增量在 ±2.0 mm之內(nèi);
(2)最后4期觀測數(shù)據(jù)(且4期觀測時間不少于1個月)未出現(xiàn)連續(xù)下沉現(xiàn)象。
工程實踐中,用數(shù)學(xué)曲線進(jìn)行路基沉降預(yù)測,而用兩個準(zhǔn)則判別墩身沉降的穩(wěn)定性,即可確定是否能夠進(jìn)行后續(xù)的布板鋪軌等工作。

