促進深度思維的數學概念教學研究*

韓龍淑 劉凱 陳錦楠

摘? ?要? 深度學習是學科核心素養培育的基礎和關鍵，數學深度學習的實質重在深度思維。以典型數學概念為例，從創設疑難情境引發概念學習需求、數學概念的自然導入、數學概念的自然生成、數學概念的變式強化和遷移、數學概念結構網絡的構建、數學概念的拓展深化等方面解析促進學生深度思維的數學概念教學路徑，提出促進深度思維的數學概念教學啟示。

關鍵詞? 深度思維? 數學概念? 疑難情境? 自然生長

深度學習是核心素養培育與發展的基本途徑[1]，是學科核心素養落地生根的關鍵。而數學是思維為主的科學，數學教學的價值在于思維教學[2]，在于啟發學生學會數學思考，因此數學深度學習的實質重在深度思維。其中數學深度思維主要體現為數學思維的活躍度、數學思維的含量、數學思維的層次和數學思維的強度，旨在優化思維策略，完善數學思維品質，促進數學深層理解和變式遷移。

《義務教育數學課程標準（2011年版）》指出：數學知識的教學，要注重知識的“生長點”與“延伸點”[3]。研課中發現，學生若缺乏對數學概念產生的必要性和合理性的感悟，未引發學習新概念的情感需求和思維需求，則容易導致數學概念的機械學習或表層學習，因此基于促進深度思維進行數學概念的教學研究具有重要意義。

一、促進深度思維的數學概念教學路徑

學源于思，思源于疑。深度思維源于強烈的認知沖突、疑難困惑并生成問題。鑒于目前多數教師對“為什么教學新概念”缺乏足夠的認識，致使數學新概念產生的必要性和價值體現不夠，未能使學生感悟學習新概念的現實需要和數學自身發展的需要，從而不易形成認知和情感的內在學習需求。因此促進學生深度思維的數學概念教學首先需要研究“為什么學習此概念”，激活學習新概念的情感需求和認知需求（Why）;其次需要研究“學習數學概念的哪些內容”（What），挖掘數學概念的本質及生成過程等。要促進學生的深度思維，提升數學思維的活躍度、含量、層次和強度，數學概念應盡量以“概念形成”的方式進行學習，使學生經歷概念形成的過程。如表1所示。

1.創設疑難情境提出問題，引發學習新概念的情感需求和思維需求

深度思維源于情境中自然生成的疑難和困惑。通過創設疑難情境、營造知識缺口，引導學生在已有知識和經驗基礎上激活思維、產生困惑并發現提出問題，引發新概念產生的情感需求和思維需求。

無理數是中學數學核心概念，其發現在數學發展史上經歷了艱難曲折的過程，是初中數學教學的難點。課堂觀察發現：初中生只知道“無理數是無限不循環小數”，再問什么是無限？什么是不循環？學生往往模棱兩可，表現出對無理數概念本質認識的茫然。

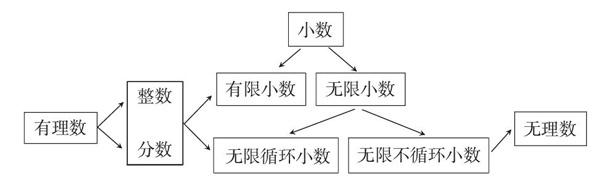
問題1：前面我們學習了有理數，有理數包括整數和分數，如果將下列整數或分數寫成小數形式，你有哪些發現？

遵循知識的發生發展過程和學生頭腦中與新知識有實質性聯系的適當觀念，啟發學生發現有理數可表示為有限小數或無限循環小數，并把有理數的小數表示作為新知識的生長點。

2.感悟數學概念產生的必要性和自然性，提升數學思維的層次和活躍度

以學生認知結構中與新概念有自然的、內在聯系的已有知識作為新概念的生長點，使新舊概念之間產生非人為和實質性聯系，感悟數學概念導入的自然性和必要性，從而提升數學思維的層次和活躍度。

問題2：是否存在無限不循環的小數呢？圓周率你能寫到多少位？教師借助PPT整屏幕展示圓周率的近似值：3.14159265358979323846264……，使學生直觀感知圓周率的精確值書寫不完，是無限且不循環的小數。

體驗無理數產生是數學自身邏輯發展的需要。

問題3：數學發展史上畢達哥拉斯學派的門徒西帕索斯發現邊長為1的正方形的對角線不能用整數或整數比表示。而邊長為1的正方形的對角線是腰為1的等腰直角三角形的斜邊，啟發學生自然思考腰為1的等腰直角三角形的斜邊長a。借助等腰直角三角形面積的兩種不同表征，邏輯推理得到[7]a2=2，斜邊的長是多少呢？1

學生感悟到有限小數和無限循環小數不夠用了，由于數學自身發展的需要自然會出現無限不循環小數，而不是人為造出的，感悟無限不循環小數存在的自然性和合理性。

無限和不循環理解起來有難度，學生不易建構無理數概念。通過邏輯推理而不是動手操作的拼補圖形，探索等腰直角三角形斜邊的長，提升了數學思維的層次和活躍度。

3.經歷概念抽象概括的自然形成過程，提升數學思維的含量和強度

要促進學生的深度思維，提升數學思維的含量和數學思維的強度，數學概念盡量以“概念形成”的方式進行學習，使學生經歷概念獲得的辨別-分化-抽象—概括—檢驗—表示等思維活動過程。

問題4：結合圓周率的值：3.14159265358979323846264……，a2=2時a的值，0.5050005000005...（相鄰兩個5之間0的個數逐漸加2），啟發學生對情境進行辨別和分化，自然抽象概括無理數是無限不循環的小數，或者不能表示成兩整數之比的數。

通過三個變式情境啟發學生結合有理數概念的經驗以及對無理數來源的認識，抽象概括無理數概念的本質，體現數學概念的自然形成過程。

4.通過正反例變式強化，促進數學概念的深層理解和拓展度

促進學生對數學概念的深層次理解，需要通過正反例的變式強化，變更數學概念的非本質屬性，突出數學概念的本質特征，并將所學概念靈活遷移到問題解決中，達到數學概念的深層理解和深度遷移。

①下面各數中哪些是有理數？哪些是無理數？

3.14，-■，0.■，0.1010001000001（相鄰兩個1之間0的個數逐漸加2），

②（1）假設面積為10的正方形的邊長為x，x是否為有理數？說說你的理由

（2）對x的值進行估計（答案精確到0.1），并用計算器或機驗證估算結果

（3）如果結果精確到0.01呢？

通過正反例變式強化無理數概念，理解無限不循環小數的本質，并鞏固用有理數估算無理數的方法，借助計算機進行檢驗，與現代信息技術深度融合。

5.構建數學概念網絡系統，體驗概念自然生長的思維主線和思維方法的關聯度

知識經過分類組織具有結構后，才易于理解、遷移和運用。梳理并提煉數學概念自然生長的思維主線和思維方法，通過概念之間的橫縱向關聯度，構建數學概念網絡系統，形成組織良好的概念網絡結構。

引導學生構建知識結構體系，建立新舊知識之間的縱橫聯系，促進對新概念的深度思維和深層理解，旨在形成組織良好的數學認知結構網絡。

6.認識數學概念的歷史發生過程，感悟數學的理性思維價值和延伸度

呈現數學發展史上無理數產生的艱難曲折歷程，并用反證法邏輯推理得到平方為2的數是無理數。通過體味數學新概念產生的歷史發生過程和思考方法，對數學概念進行深度加工和拓展深化，使學生感悟數學的理性思維等文化價值，提升數學思維的延伸度。

二、促進深度思維的數學概念教學啟示

1.讀懂并創造性運用教科書，把握數學概念的本質

一節自然生長且促進深度思維的數學概念課，關鍵在于深層理解概念并能遷移運用概念。教師在教學設計時，需要深層理解教科書，并對不同版本教科書內容進行精選和整合。

目前有兩個以上版本的初中數學教科書中，無理數概念的引入是把兩個邊長為1的小正方形“剪一剪，拼一拼”，得到一個大正方形，發現面積為2的正方形的邊長是無理數。雖然剪和拼也可以產生無理數，但是剪和拼的動手操作和直觀感知比較突兀，為什么要通過“剪和拼”得到一個大正方形呢？學生缺乏對無理數概念產生的抽象過程的體驗，降低了數學思維的抽象層次。通過啟發學生邏輯推理發現腰為1的等腰直角三角形斜邊長的平方為2，以此探索平方為2的數的本質特征。既提升了理性思維的層次和思維的強度，又有利于抽象無理數概念的本質，體現概念的生長到思維和智慧的生長。

2.盡可能使學生感悟數學新概念產生的必要性和自然性

通過現實需要的分析，讓學生感悟數學與現實及其他學科的聯系，產生概念學習的情感需求;通過數學自身發展需要的分析，使學生產生數學概念學習的思維需求。

深度思維重在使學生體驗到數學概念等的起源與發展是自然的，是已有數學概念不夠用了，是水到渠成和有人情味的，從而經歷概念產生過程中的火熱數學思考，在頭腦中展開高水平的數學思維活動，感悟數學概念產生的必要性、自然性和合理性。教學中需要教師創設疑難、困惑的“憤悱”情境，并運用啟發性提示語、合乎情理地引導學生探索數學概念的自然生成，從而使鮮活的數學概念在學生頭腦中自然而然地流淌出來。

3.課堂小結重在使學生構建數學概念圖，形成組織良好的認知結構網絡

課堂小結是數學概念教學的重要環節之一，旨在對所學概念進行梳理歸納、改造重組和系統提升。對強化數學概念、啟迪學生深度思維、形成數學概念網絡和促進數學遷移具有重要作用。概念教學中教師盡量，引導學生歸納概念的本質和研究方法等，并輔以文字、圖表等搭建數學概念網絡圖。網絡的節點越多，通道越豐富，概念理解越深刻，從而形成組織良好的數學概念認知結構網絡。以此促進數學深度思維，切實提升數學學科核心素養。

參考文獻

[1] 郭華.深度學習與課堂教學改進[J].基礎教育課程，2019（02）.

[2]卜以樓.生長數學：數學教學的理性回歸[J].中國數學教育，2017（09）.

[3] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[4] 曹才翰，章建躍.數學教育心理學（第3版）[M].北京：北京師范大學出版社，2017.

[5] 范芬瑞，韓龍淑.基于PCK視角的數學原理的教學設計—以勾股定理為例[J].天津師范大學學報：基礎教育版，2018，19（04）.

[6] 韓龍淑.數學教材分析中發展應用意識素養的雙向路徑[J].教學與管理，2018（02）.

[作者：韓龍淑（1965-），女，山西榆次人，太原師范學院數學系，教授，博士;劉凱（1995-），女，山西交城人，太原師范學院教育學院，碩士生;陳錦楠（1997-），女，天津人，太原師范學院教育學院，碩士生。]【責任編輯? 劉永慶】