關節鉸接雙面接觸摩擦對醫用機械臂影響分析
,
(蘭州理工大學機電工程學院,甘肅 蘭州 730050)
0 引言
醫用機械臂是放射治療系統中的主要組成部分之一,其作用是支撐患者進行擺位將靶區(腫瘤)置于束流照射范圍內[1-2]。關節主要由電機、RV減速器、連接法蘭等構成。其大臂、小臂的臂桿較長,重量較大且其運動平面與地面平行,因此在關節鉸接圓柱面及端面都會出現摩擦,造成大量能量損失。文獻[3]表明,機械臂關節上的驅動力矩(驅動力)大約有20%消耗在克服摩擦阻力上,關節摩擦不僅造成能量損耗還對機械臂的動力學特性產生影響。文獻[4]表明關節摩擦的存在對機械臂速度及加速度的影響明顯。文獻[5]得出關節摩擦存在時,機器人低速的運動性能會惡化且對作業精確度影響較大。
在此,以醫用機械臂為研究對象,基于庫侖摩擦模型,利用拉格朗日方程分別建立不包含摩擦和包含關節鉸接圓柱面及端面摩擦的動力學模型,并進行仿真分析這2處摩擦對關節輸出扭矩及機械臂末端位置軌跡的影響。
1 不考慮摩擦時三桿醫用機械臂動力學建模
醫用機械臂三維模型如圖1所示,對醫用機械臂做如下假設:每個桿和關節都是剛性體;每個關節都只有1個轉動的自由度。

圖1 醫用機械臂三維模型
由于拉格朗日法在分析多關節動力學特性上不涉及到約束力[6],所以采用拉格朗日法來建立動力學模型。保守系統的拉格朗日方程形式為[7]
(1)

L=T-V
(2)
T為系統總的動能;V為系統總的勢能。
將醫用機械臂簡化成如圖2 所示的三桿結構,并建立固定坐標系OXY及參考坐標系O1X1Y1Z1,O2X2Y2Z2,O3X3Y3Z3,如圖3所示。
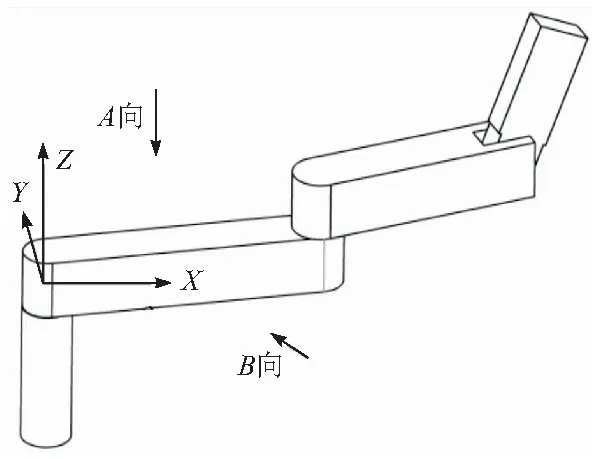
圖2 醫用機械臂簡化示意
各桿質心位置分別為m1,m2,m3;繞質心的轉動慣量為IC1,IC2,IC3;LC1,LC2,LC3為各關節軸中心到相對應桿質心的距離;L1,L2,L3為各關節中心垂直距離。根據圖3利用幾何法求得各桿質心坐標位置矢量。
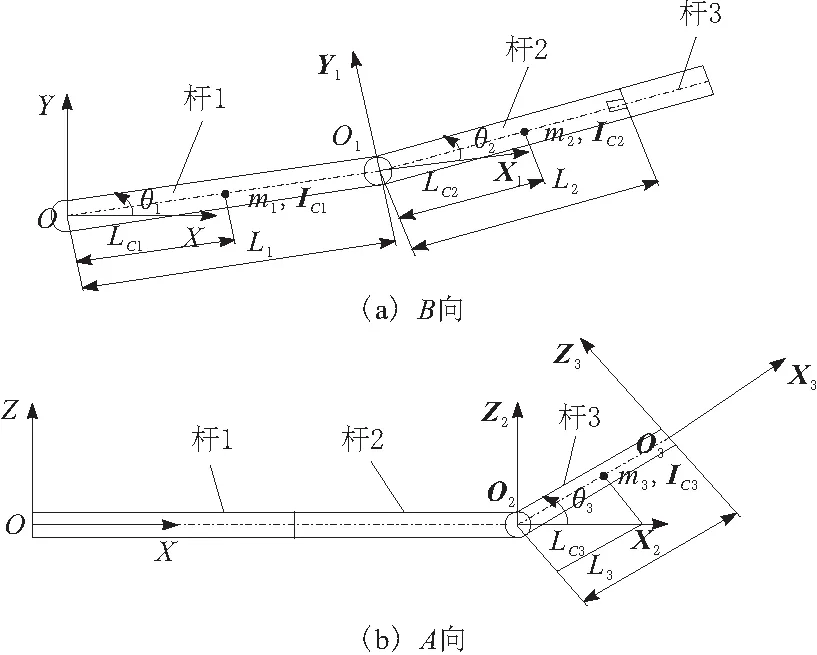
圖3 醫用機械臂坐標系
桿1質心坐標為
(3)
桿2質心坐標為
(4)
桿3質心坐標為
(5)
因為各桿繞定軸轉動可以表示為質心的平移運動和繞質心的旋轉運動2個運動的合成,所以系統總動能為
(6)
系統總勢能為
(7)


(8)

2 含摩擦的動力學建模
含摩擦的機械臂動力學模型基本形式為[8]
(9)

(10)
Tf1,Tf2,Tf3為各關節處總摩擦力矩,大小與所選的摩擦模型有關。本文選取庫倫摩擦模型[9]為
(11)

Tn=Fnr
(12)
Fn為法向接觸力;r為作用半徑。
2.1 法向接觸力求解
首先將三桿醫用機械臂各關節簡化成如圖4所示的接觸形式,并將鉸接圓柱面及端面描述成接觸面1和接觸面2。利用達朗伯定理對其進行動靜力學分析,分別如圖5和圖6所示。

圖4 鉸接簡化示意

圖5 B向醫用機械臂受力分析
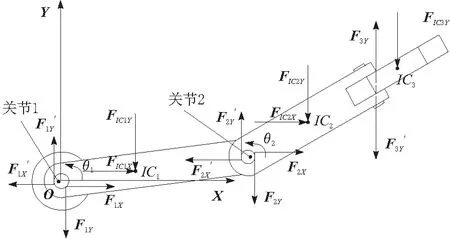
圖6 A向醫用機械臂受力分析

以桿1為研究對象:
(13)
以桿2為研究對象:
(14)
以桿3為研究對象:
(15)

(16)
(17)
(18)
現定義接觸系數α1和α2分別表示關節1和關節2的鉸接接觸面2的接觸程度,其值與關節的結構、剛度、臂桿長度、裝配精度等有關,且接觸面2實際接觸力與α1和α2成正比,則關節1和關節2鉸接接觸面2上接觸力為
(19)
2.2 摩擦力矩求解
桿2與桿3之間相對運動速度較慢,所以忽略關節3處摩擦以簡化問題的研究。庫倫摩擦模型下關節1和關節2與接觸面1上摩擦力引起摩擦力矩分別為:
(20)
(21)
u1,u2為關節1和關節2的兩觸面摩擦系數;r1和r2為作用半徑;Tf′1X,Tf′1Y,Tf′2X,Tf′2Y為關節1和關節2在X軸、Y軸上的接觸力作用下產生的摩擦力矩。接觸面2摩擦力產生摩擦力矩為:
(22)
(23)
Tf″1為關節1與接觸面2處的摩擦力矩;Tf″2為關節2與接觸面2處的摩擦力矩;R1為關節1與接觸面2的外徑;R2為關節2與接觸面2的外徑;u3為關節1與接觸面2的摩擦系數;u4為關節2與接觸面2的摩擦系數。
庫侖摩擦模型下各關節總摩擦力矩為
(24)
3 仿真分析
利用MATLAB對不含摩擦模型及含有庫倫摩擦模型的動力學方程下的關節1和關節2輸出扭矩進行仿真分析,表1為機械臂結構參數,表2為機械臂仿真運動參數。令R1=20 cm,R2=15 cm;r1=r2=10 cm。

表1 醫用機械臂主要參數
圖7和圖8為醫用機械臂在表2的運動參數下,不考慮摩擦及分別考慮接觸面1和接觸面2摩
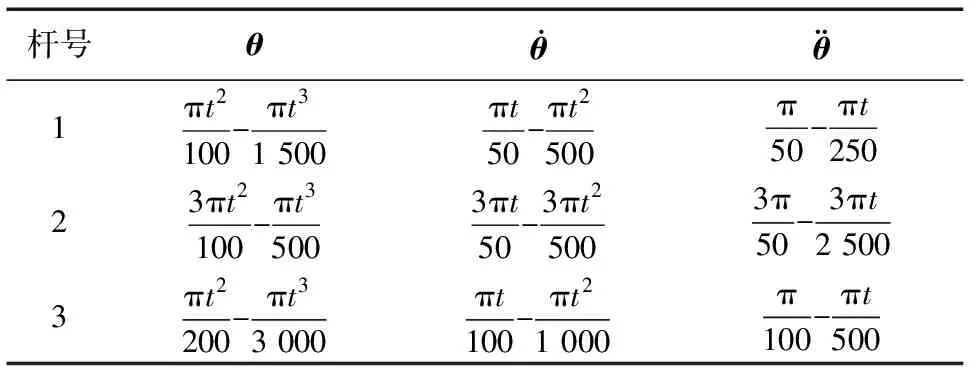
表2 醫用機械臂運動參數
擦時,關節1和關節2在1~10 s的輸出轉矩。由圖7和圖8可以看出:在相同摩擦系數下, 當接觸面系數α大于0.01時接觸面2對關節輸出扭矩的影響大于接觸面1,隨著α增大影響更加明顯,而接觸面1對輸出扭矩的影響隨著摩擦系數增大變化不明顯,與現實情況比較相符。
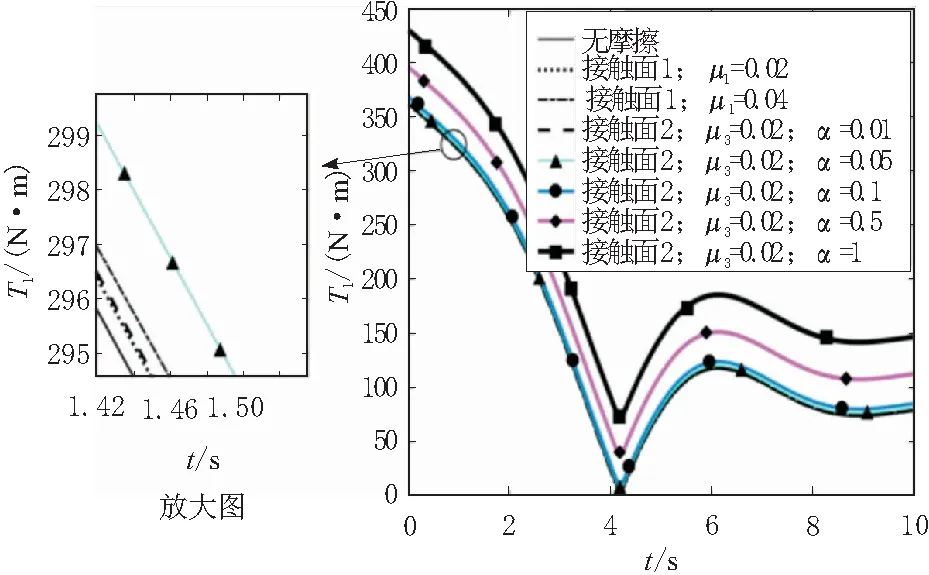
圖7 關節1輸出轉矩

圖8 關節2輸出轉矩
圖9~圖14為3個關節輸出扭矩分別為T1=300 N·m,T2=200 N·m,T3=10 N·m下不考慮摩擦及不同摩擦狀況下的末端位置仿真結果。圖9和圖10分別考慮關節1處接觸面1和接觸面2時機械臂末端軌跡,從圖9~圖10中看出,接觸面1對機械臂末端軌跡影響遠小于接觸面2,隨著接觸面系數增大影響越來越明顯,軌跡呈現不規則現象。圖11~圖14為考慮關節1的2個接觸面摩擦分別與關節2的2個接觸面摩擦耦合下的機械臂末端軌跡,可以看出當2個面都為接觸面1時軌跡變化最小。

圖9 關節1處接觸面1摩擦時機械臂末端軌跡

圖10 關節1處接觸面2摩擦時機械臂末端軌跡

圖11 關節1、關節2處接觸面1摩擦時機械臂末端軌跡

圖12 關節1處接觸面1及關節2接觸面2摩擦時機械臂末端軌跡

圖13 關節1處與接觸面2及關節2接觸面1摩擦時機械臂末端軌跡

圖14 關節1、關節2處接與觸面2摩擦時機械臂末端軌跡
4 結束語
以醫用機械臂為研究對象,基于拉格朗日方程并利用達朗伯定理建立了不包含摩擦及包含摩擦的2種動力學模型,同時引入接觸面系數α1和α2。通過仿真分析得出當關節鉸接的2個接觸面摩擦系數相同時,鉸接端面(接觸面2)的接觸面系數超過一定范圍時對關節輸出扭矩影響明顯大于鉸接圓柱面(接觸面1)影響,同時也會造成巨大的能量損失,因此在設計制造過程中可以通過提高關節剛度,減小桿的長度,提高裝配精度等方法減小關節鉸接端面的接觸程度。通過對機械臂末端軌跡仿真分析可知:鉸接端面對機械臂末端軌跡影響明顯大于鉸接圓柱面,因此在精度要求較高的情況下,對于與本文的醫用機械臂及結構相類似的機械臂,對其建模時應該著重分析關節鉸接端面的接觸程度且不可以忽略,以免造成巨大的能量損失及誤差。

