耦合Riccati方程數值迭代方法
, , ,
(湖南工業大學 理學院,湖南 株洲 412007)
1 研究背景
本文考慮一類耦合非對稱代數Riccati方程(coupled nonsymmetric algebraic Riccati equation,CNARE)

式中:Xi∈Rn×n為方程的解,i,j∈U={1,2,…,s},其中s是大于1的整數;
Ai∈Rm×m,Bi∈Rm×n,Ci∈Rn×m,Di∈Rm×n為方程的系數矩陣;
eij為非負常量,且滿足列和為1。
此類方程在粒子輸運理論[1-2]、控制理論[3]和馬爾可夫鏈[4-6]等領域中有著廣泛而深入的應用。在實際建模中,人們對此類方程感興趣的是其具有實際意義的最小非負解。特別地,當s=1時,耦合方程(1)還原成非對稱Riccati方程
Q(X)=XCX-XD-AX+B=0。
其最小非負解的存在性和相關數值求解方法已經得到了充分的研究[7]。
為了更好地研究更廣泛的耦合方程(1)的最小非負解的存在性和相關的數值迭代方法,本文將耦合方程(1)寫成如下統一形式:
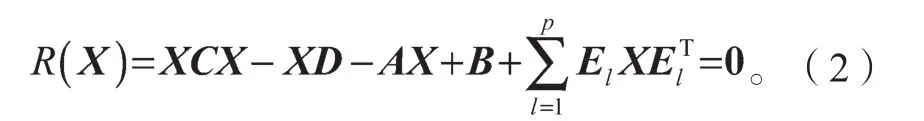
El為只有(i,j)塊和(j,i)塊分別為eijIn和ejiIn,其余塊都為0的矩陣,共有p=s(s-1)/2個。
2 定義與預備定理
對任何矩陣A和B,A>B(A≥B)表示矩陣A中所有元素大于(大于或等于)矩陣B中的所有元素,特別地若A≥0,則稱A為非負矩陣。
定義1[8-9]若矩陣A∈Rn×n的非對角元非正,則稱A為Z-矩陣。
任何Z-矩陣都可寫成sI-B,其中B≥0。
定義2[8-9]若s≥ρ(B),Z-矩陣A=sI-B(B≥0)稱為M-矩陣。特別地,若s=ρ(B),稱A為奇異的M-矩陣;若s>ρ(B),稱A為非奇異的M-矩陣,其中ρ(B)為B譜半徑。
定理1[10]對Z-矩陣A,下述命題等價:
1)A是非奇異的M-矩陣;
2)A是非奇異矩陣且滿足A-1≥0;
3)存在某一向量v>0使Av>0;
4)A的所有特征值都有正的實部。
定理2[10]設A∈Rn×n是一個M-矩陣,如果B∈Rn×n中的元素滿足關系bii≥aii,aij≤bij≤0,i≠j,1≤i,j≤n,則B也是一個M-矩陣。
本文假設耦合方程(2)滿足如下條件:

注1 由克羅內克積的性質可知,當且僅當A,D和E是Z-矩陣時IA+DTI-∑ElEl也是Z-矩陣。在不混淆的情況下,本文從此開始省略求和符號∑的上下標。
3 迭代方法
3.1 牛頓迭代
考慮對耦合方程(2)的牛頓迭代法。假設Rm×n是Banach空間,R是Riccati函數在空間Rm×n到自身的映射,則其Frechet導數為[12-13]


則求解耦合方程(2)等價于如下迭代格式:

對上述牛頓迭代格式有如下收斂性定理3。
定理3如果存在一個非負矩陣X使得方程(2)滿足R(X)≤0,且條件(3)成立,則對上述非負矩陣X,一定存在(2)的一個非負解S使得S≤X,特別地,S是方程(2)的最小非負解。此外,對于牛頓迭代格式(4),當X0=0時,序列{Xi}是適定的,并滿足

而且矩陣
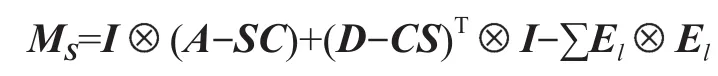
也是一個M-矩陣。
證明設X為任意一個非負矩陣,使得
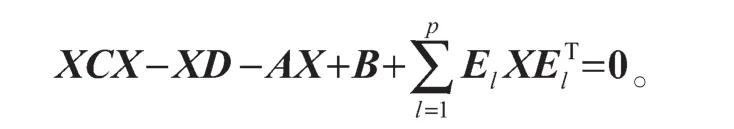
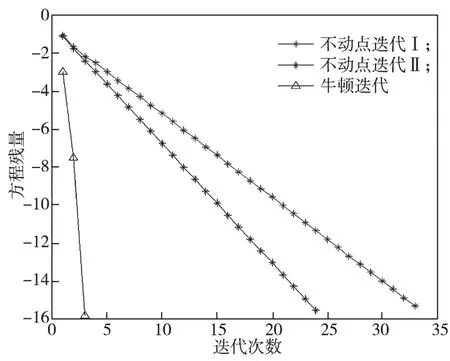
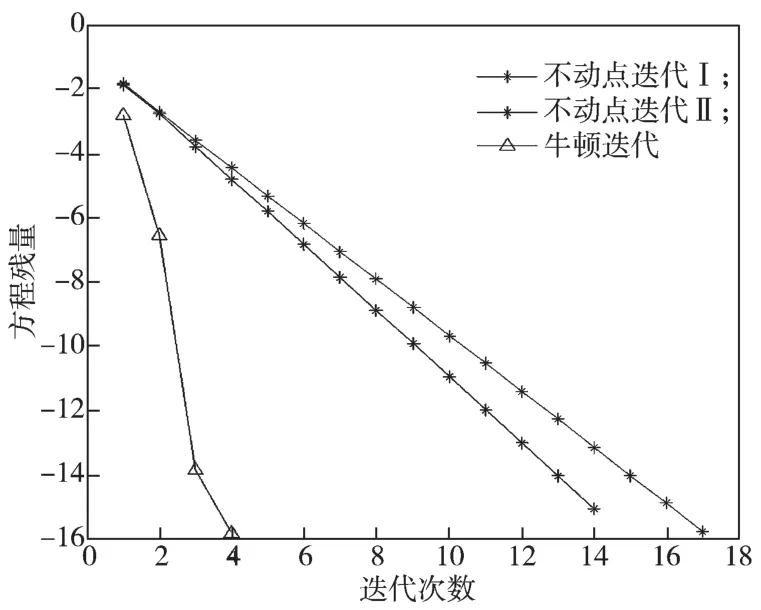
對于牛頓迭代式(4),用數學歸納法證明對所有的k滿足:Xk 是非奇異M-矩陣。 當X0=0時,有 即有 式中vec運算是將矩陣的列轉化成一個長矢量[14]。 設當k=i≥0時歸納假設成立。 由式(2)和式(4)得 (A-XiC)(Xi+1-X)+(Xi+1-X)(D-CXi)-∑El(Xi+1-X)El= B-XiCXi-AX+XiCX-XD+XCXi=-(Xi-X)C(Xi-X)。 因為Xi 另一方面,由式(4)得 由式(2)和式(6)可得 (A-Xi+1C)(Xi+1-X)+(Xi+1-X)(D-CXi+1)-∑El(Xi+1-X)El= -(Xi+1-Xi)C(Xi+1-Xi)-(Xi+1-X)C(Xi+1-X)<0。即有 因此由定理1中的命題3)可知, 是非奇異M-矩陣。 再次由式(4)和式(6)可得 因此有Xi+1 最后,假設對所有的i≥0,非奇異M-矩陣 注2 上述結果與文獻[13]中定理9.1.1有相似的性質。 將耦合方程(2)中系數矩陣A、D進行分解,寫成 A=A1-A2,D=D1-D2, 且滿足A2,D2≥0,A1,D1是Z-矩陣。則耦合方程(2)變為 其中線性算子 定理4如果對于非負矩陣X,R(X)≤0,則由不動點迭代式(8)給定初始迭代點X0=0,對任意的k≥1有 證明對不動點迭代式(8),采用數學歸納法證明 Xk 當k=0時,有 這個方程等價于 設當k=i≥0時歸納假設成立。 由式(7)和式(10)得 另一方面,由式(10)得 因此有Xi+1 本章通過數值實驗驗證牛頓迭代和不動點迭代的收斂理論,并比較兩種迭代方法的數值表現。計算采用Matlab 14a編程,其機器精度為2-53,約為2.2e-16。在不動點迭代法中,矩陣A1和D1分別為矩陣A和D的對角矩陣和下三角矩陣,記為不動點迭代I和不動點迭代II。當兩類算法方程殘量小于10-15時,終止算法。方程殘量的計算公式為 例1考慮一類耦合非對稱代數Riccati方程(1),其對應的系數矩陣為 解分別采用牛頓迭代和兩類不動點迭代方法編程求解上述問題。當所有算法終止后,將迭代次數和方程殘量列于表1中。 表1 例1中牛頓迭代與不動點迭代數值表現Table1 Numerical representation of Newton’s method and two fixed-point iterations in example 1 從表1可以看出,迭代終止時,牛頓法迭代次數比不動點迭代I和不動點迭代II少很多。迭代終止時,牛頓法迭代能獲得比不動點迭代I和不動點迭代II更小的方程殘量。對兩種不動點迭代而言,不動點迭代II的迭代次數比不動點迭代I少,其獲得的方程殘量也比不動點迭代I更小。實際上,不動點迭代I等價于Jacobi迭代,而不動點迭代II等價于Gauss-Seidel迭代。 圖1為3種迭代方法方程殘量的歷史圖。從圖中可以看出,牛頓迭代法是二次收斂,而兩種不動點迭代都是線性收斂,但不動點迭代II比不動點迭代I在每步都能獲得更小的方程殘量。 圖1 例1中牛頓迭代與不動點迭代方程殘量歷史圖Fig.1 Residual history diagram for Newton’s method and fixed-point iteration equation in example 1 例2考慮一類耦合非對稱代數Riccati方程(1),其對應的系數矩陣為 解與例1類似,分別采用牛頓迭代和兩類不動點迭代方法編程求解上述問題。當所有算法終止后,將迭代次數和方程殘量列于表2中。 表2 例2中牛頓迭代與不動點迭代數值表現Table2 Numerical representation of Newton’s method and two fixed-point iterations in example 2 從表2可以得出,當迭代終止時,牛頓法所需的迭代次數比不動點迭代要少得多,而且能獲得更小的方程殘量。 圖2為3種迭代方法方程殘量的歷史圖。從圖中可以看出牛頓法迭代是二次收斂的,而2種不動點迭代都是線性收斂。 圖2 例2中牛頓迭代與不動點迭代方程殘量歷史圖Fig.2 Residual history diagram for Newton’s method and fixed-point iteration equations in example 2 本文采用牛頓迭代法和不動點迭代法求解一類非對稱耦合的Riccati方程。在一定條件下證明了這兩種迭代方法單調收斂到具有實際意義的最小非負解,數值實驗驗證了提出方法的有效性。


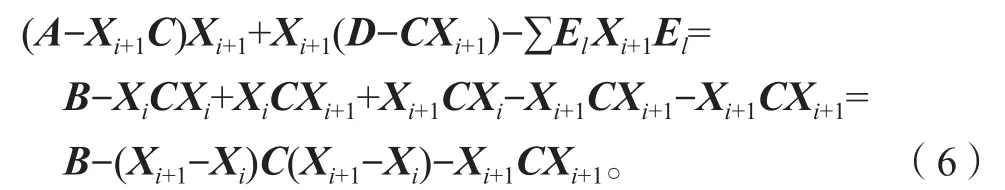
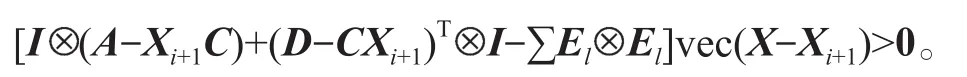
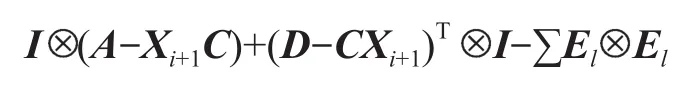


3.2 不動點迭代
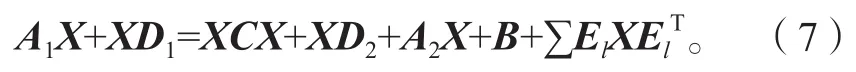
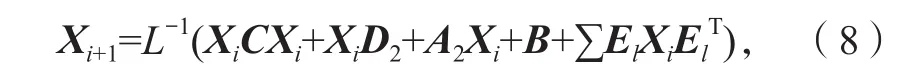
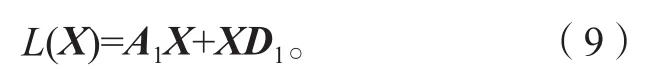
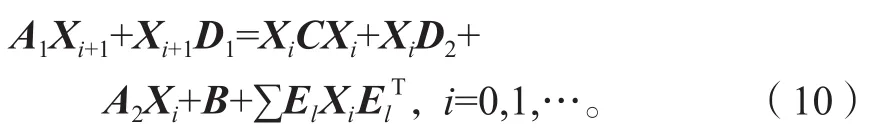




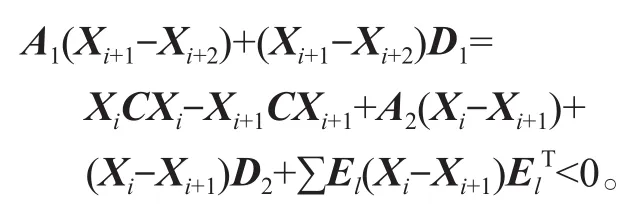
4 數值實驗





5 結語

