災變模型在馬尾松毛蟲幼蟲發生量預報中的應用

張書平， 余 燕， 畢守東， 周夏芝， 鄒運鼎， 張國慶， 張 楨， 方國飛， 宋玉雙

（1. 安徽農業大學 理學院， 安徽 合肥230036； 2. 安徽農業大學 林學與園林學院， 安徽 合肥230036；3. 安徽省潛山縣林業局， 安徽 潛山246300； 4. 國家林業和草原局 森林病蟲害防治總站， 遼寧 沈陽110034）

馬尾松毛蟲Dendrolimus punctatus分布于安徽、 河南、 四川、 貴州、 陜西、 云南、 江西、 江蘇、 湖南、 浙江、 福建、 廣東、 海南和廣西等， 主要危害馬尾松Pinus massoniana， 還危害黑松Pinus thunbergii， 火炬松Pinus taeda， 濕地松Pinus elliottii， 晚松Pinus rigidavar.serotina和海南松Pinus fenzeliana等松屬Pinus植物。 20 世紀中葉在中國森林害蟲中馬尾松毛蟲是發生最廣、 危害面積最大、 經常猖獗成災的害蟲。 在廣大丘陵地區蟲害此起彼伏， 為害時如同火燒， 造成了巨大的經濟效益和生態效益損失。該蟲不但影響林業生產， 還危害人身健康［1-4］， 人們的林事活動中接觸馬尾松毛蟲毒毛， 容易引發皮炎和關節腫痛。 進入21 世紀， 封山育林、 混交、 間作等措施優化了森林生態環境， 使馬尾松毛蟲的危害得到有效控制， 但該蟲具有強大的繁殖潛力， 遇到有利的生態環境極易爆發成災， 不能放松對它的監測。 馬尾松毛蟲1 a 發生2～4 代， 發生世代的多少隨不同地方而異。 在河南省信陽地區1 a 發生2 代為主， 在長江流域諸省1 a 發生2～3 代， 而在廣東、 廣西、 福建南部1 a 發生3～4 代， 海南1 a 發生4～5代［1］。 安徽潛山縣1 a 發生3 代， 即4-6 月上旬為越冬代， 6 月上旬至8 月中下旬為1 代， 8 月中下旬至12 月為2 代。 馬尾松毛蟲發生的預測預報是對其進行綜合防治的基本工作。 研究者［5-9］分別采用不同的預測方法預測馬尾松毛蟲的發生量、 蟲害等級、 發生類別、 發生空間格局， 為馬尾松毛蟲的綜合防治工作提供了有力支持。 由于各地氣象條件、 植被條件和地形地貌等不同， 馬尾松毛蟲的發生特點也不完全相同。 為了有效地防治馬尾松毛蟲， 本研究采用灰色理論中的災變預測法研究了安徽省潛山縣馬尾松毛蟲幼蟲越冬代、 1 代和2 代嚴重發生的年份， 以期為馬尾松毛蟲的綜合治理提供科學依據。

1 材料與方法

1.1 材料來源

馬尾松毛蟲資料來自國家林業和草原局森林病蟲中心測報點——安徽省潛山縣森林病蟲防治站， 時間跨度為1989-2016 年， 其中1998 年缺失。 采用踏查和詳查相結合的方法， 沿林班線、 林道、 公路、鐵路等線路調查， 目測發生范圍、 危害狀況， 發現蟲情或災情立即設臨時標準地， 采取平行線抽樣法抽取20 株標準株詳查。 幼蟲期調查， 1～2 齡幼蟲調查枯黃卷曲的枝數， 推算幼蟲數， 3 齡以上的幼蟲且3 m 以下的小樹直接調查合計樹冠上的幼蟲數， 大樹用“蟲糞粒推算法” 調查， 幼蟲越冬期間調查樹干基部樹皮縫中的幼蟲數推算全部蟲口。

1.2 災變預測的建模方法

灰色系統理論認為， 一切隨機量都是在一定范圍內、 一定時段上變化的灰色量及其灰色過程， 主張從事物內部研究其發展變化規律。 對于灰色量的處理， 不是去尋求它的統計規律和概率分布， 而是從無規律的原始數據中找出規律， 即對數據通過一定方式處理后再建立模型。 因為客觀系統無論怎樣復雜，它總是有關聯、 有序、 有整體功能的， 作為系統行為特征的數據， 總是蘊含著某種規律。

如果在x（0）中有新的數列n′＜n是符合災變定義的數列， 則對于上災變其中：i′為災變年序號，V′為災變年序號取值范圍。

為了便于辨認， 特記災變年序號i′為z（i′）或z（i）。 并作災變號映射記z的1 次累加生成數（accumulated generating operation，則災變預測的GM（1,1）模型有如下算式：其中：t為年份，a為發展灰數，u為內生控制灰數，為待估灰數， B 為累加矩陣， BT為轉置矩陣，yN為常數項向量。

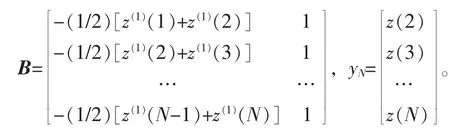
2 結果與分析

2.1 馬尾松毛蟲累計蟲口數

馬尾松毛蟲每年越冬代、 1 代幼蟲和2 代幼蟲的累計蟲口數見表1， 將其作為原始數據。

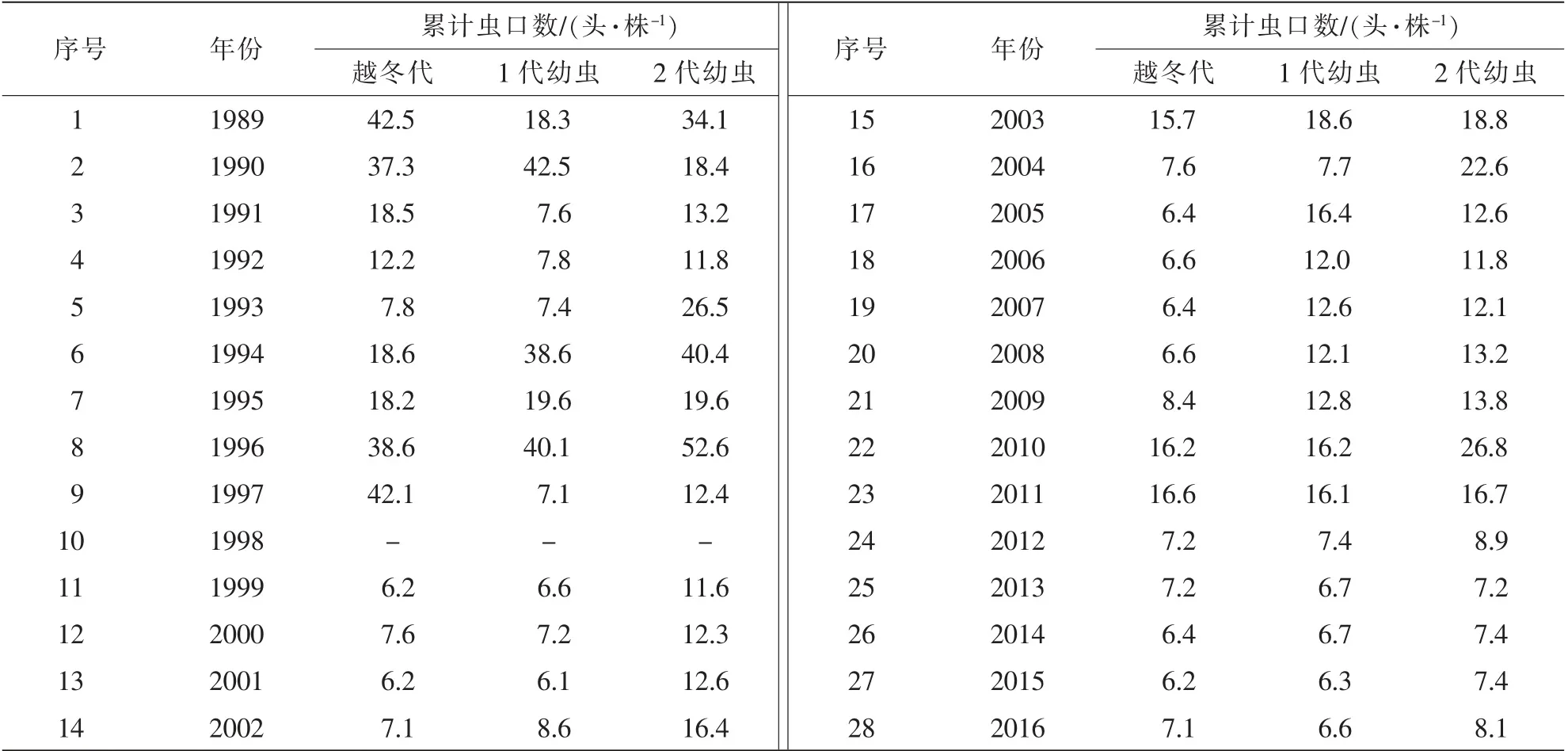
表1 馬尾松毛蟲越冬代、 1 代幼蟲和2 代幼蟲累計蟲口數Table 1 Accumulative population of D. punctatus during wintering, first and second generation larvae

2.2 馬尾松毛蟲越冬代災變預測

2.2.1 確定災變閾值 根據安徽省潛山縣森林病蟲害防治總站提供的1983-2016 年馬尾松毛蟲發生情況的資料， 馬尾松毛蟲越冬代蟲口數大于15 頭·株-1的年份為大發生年， 故以每株蟲口數15 頭為災變閾值。

2.2.2 對原始數列作有關映射 原始數列為x（0）={x（0）（1）， x（0）（2）， …， x（0）（28）}={42.5， 37.3， 18.5，12.2， 7.8， 18.6， 18.2， 38.6， 42.1， 6.2， 7.6， 6.2， 7.1， 15.7， 7.6， 6.4， 6.6， 6.4， 6.6， 8.4， 16.2，16.6， 7.2， 7.2， 6.4， 6.2， 7.1}。 對原始數列作災變映射， 按ξ≥15 得災變數列：

然后再作災變序號映射p，p{xξ（0）}={z}，pxξ（0）={z（1′），z（2′），z（3′），z（4′），z（5′），z（6′），z（7′），z（8′），z（9′），z（10′）}={1′， 2′， 3′， 4′， 5′， 6′， 7′， 8′， 9′， 10′}=z。

由于1′=1， 2′=2， 3′=3， 4′=6， 5′=7， 6′=8， 7′=9， 8′=15， 9′=22， 10′=23， 故得到災變日期集z={1， 2， 3， 6， 7， 8， 9， 15， 22， 23}即為建模時所需的原始數列。

2.2.3 建立灰色預測GM（1,1）模型 對災變年序集z 建立GM（1,1）模型， 按原始數列z= {1， 2， 3， 6，7， 8， 9， 15， 22， 23}作OAG（一次累加生成算子）得：

OAG{z（0）}=z（1）={z（1）（1）， z（1）（2）， z（1）（3）， z（1）（4）， z（1）（5）， z（1）（6）， z（1）（7）， z（1）（8）， z（1）（9）， z（1）（10）}={1， 3， 6， 12， 19， 27， 36， 51， 73， 96}。

按z（1）建模：由此得出馬尾松毛蟲越冬代蟲口數的GM（1,1）災變預測模型：

將根據馬尾松毛蟲越冬代蟲口數的GM（1,1）災變預測模型得到的擬合值、 誤差等列于表2。

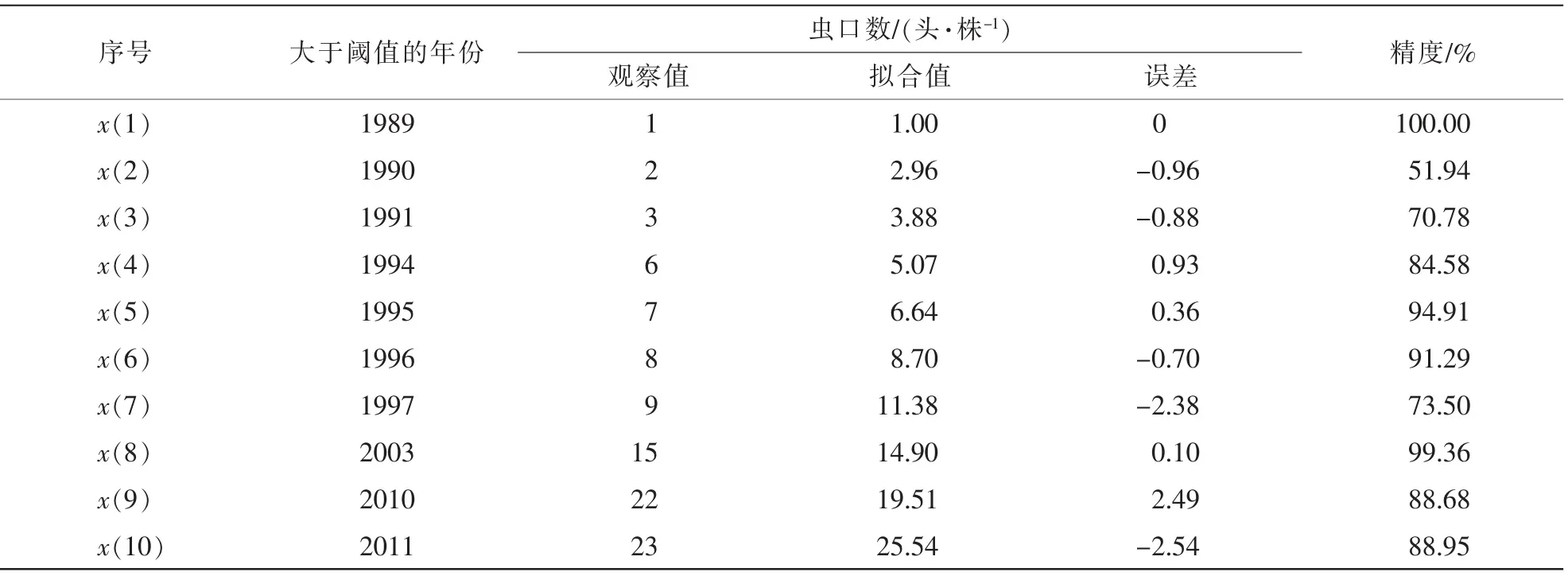
表2 馬尾松毛蟲越冬代蟲口數預測的擬合值與誤差Table 2 Fitting value and error of population prediction of D. punctatus in overwintering generation

對觀察值和擬合值間的差異進行t檢驗，t=0.101 7，df=18 時，t0.05=2.10，t＜t0.05， 差異不顯著， 平均誤差（2 個均數之差）只有觀察值均數的3.40%。 實際觀察值與通過GM（1,1）災變預測模型得到的擬合值之間誤差較小， 各災變年的平均精度為84.40%， 總體精度（觀察值的平均值減去誤差的平均值與觀察值的平均值之比） 為96.25%。 由此可以通過這個模型求得未來5 個時刻的預測值， 用所建災變預測模型z＾（1）（k+1）=9.580 75e0.26933k-8.580 75對未來馬尾松毛蟲越冬代災變年份進行預測z＾（0）（11）=z＾（1）（11）-z（1）（10）=33.434 8， 由原始序號得知， 原始序列最后一次災變是2011 年， z（0）（10）=23， 現預測下一次災變年的序號z＾（0）（11）=33.434 8， 即從2011 年馬尾松毛蟲越冬代災變年算起， 再過10 a 即2021 年為馬尾松毛蟲越冬代大發生年， 同理可預測之后年份z（t+1）=33.434 8，z（t+2）=43.769 1，z（t+3）=57.297 6，z（t+4）=75.007 5，z（t+5）=98.191 4。

2.3 馬尾松毛蟲1 代幼蟲災變預測

與上述馬尾松毛蟲越冬代蟲口數GM（1,1）災變預測模型相似， 由表1 根據閾值大于15 頭·株-1可以得到馬尾松毛蟲1 代幼蟲蟲口數GM（1,1）災變預測模型。

原始數列為x（0）={x（0）（1）， x（0）（2）， ...， x（0）（28）}={18.3， 42.5， 7.6， 7.8， 7.4， 38.6， 19.6， 40.1， 7.1，6.6， 7.2， 6.1， 8.6， 18.6， 7.7， 16.4， 12.0， 12.6， 12.1， 12.8， 16.2， 16.1， 7.4， 6.7， 6.7， 6.3， 6.6}。

對原始數列作災變映射， 按ξ≥15 得災變數列， 最終得到災變日期集={1， 2， 6， 7， 8， 15， 17，22， 23}即為建模時所需的原始數列。

作OAG得：OAG{z（0）}=z（1）={1， 3， 9， 16， 24， 39， 56， 78， 101}。

按z（1）建模：即a＾=-0.241 87，u=4.155 67，u/a=-17.181 8，z（0）（1）=1，由此得出馬尾松毛蟲1 代幼蟲蟲口數的GM（1,1）災變預測模型：

將根據馬尾松毛蟲1 代幼蟲蟲口數的GM（1,1）災變預測模型得到的擬合值、 誤差等列于表3。

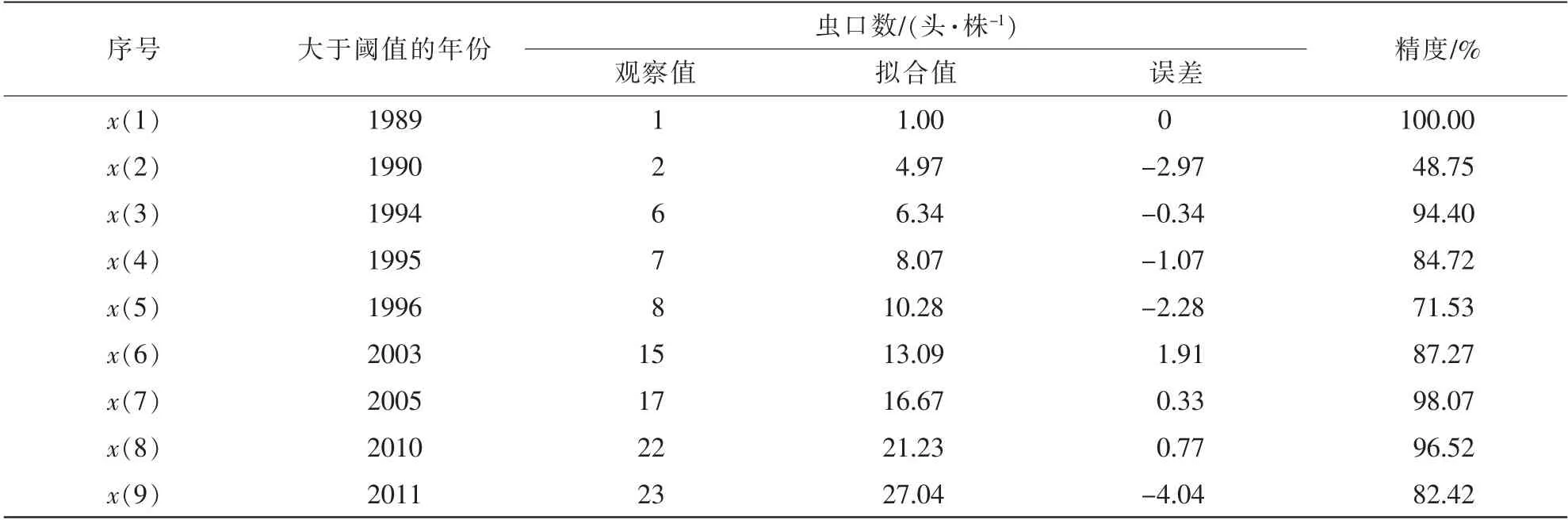
表3 馬尾松毛蟲1 代幼蟲蟲口數預測的擬合值與誤差Table 3 Fitting value and error of prediction of population number of first generation larvae of D. punctatus

對觀察值和擬合值的差異進行t檢驗，t=0.218 6，df=16 時，t0.05=2.12，t＜t0.05， 兩者差異不顯著， 平均誤差（2 個均數之差）只有觀察值均數的6.49%。 實際觀察值與通過GM（1,1）災變預測模型得到的擬合值之間誤差較小， 各災變年的精度平均為84.85%， 總體精度為92.34%。 由此可以通過這個模型求得未來5 個時刻的預測值， 用所建災變預測模型z＾（1）（k+1）=18.181 8e0.24187k-17.181 8 對未來馬尾松毛蟲一代幼蟲災變年份進行預測z＾（0）（10）=z＾（1）（10）-z（1）（9）=34.443 8， 由原始序號得知， 原始序列最后一次災變是2011年，z（0）（9）=23， 現預測下一次災變年的序號z＾（0）（10）=34.443 8， 即從2011 年馬尾松毛蟲1 代幼蟲災變年算起， 再過11 a 即2022 年為馬尾松毛蟲一代幼蟲大發生年， 同理可以預測之后年份z（t+1）=34.443 8，z（t+2）=43.868 4，z（t+3）=55.871 7，z（t+4）=71.159 5，z（t+5）=90.630 2。

2.4 馬尾松毛蟲2 代幼蟲災變預測

與馬尾松毛蟲越冬代和1 代幼蟲蟲口數GM（1,1）災變預測模型相似， 由表1 根據閾值大于15 頭·株-1可以得到馬尾松毛蟲2 代幼蟲蟲口數GM（1,1）災變預測模型。

原始數列為x（0）={x（0）（1）， x（0）（2）， ...， x（0）（28）}={34.1， 18.4， 13.2， 11.8， 26.5， 40.4， 19.6， 52.6，12.4， 11.6， 12.3， 12.6， 16.4， 18.8， 22.6， 12.6， 11.8， 12.1， 13.2， 13.8， 26.8， 16.7， 8.9， 7.2， 7.4，7.4， 8.1}。

對原始數列作災變映射， 按ξ≥15 得災變數列， 最終得到災變日期集z={1， 2， 5， 6， 7， 8， 14，15， 16， 22， 23}即為建模時所需的原始數列。

作OAG得：={1， 3， 8， 14， 21， 29， 43， 58， 74， 96， 119}。

按z（1）建模：即a＾=-0.197 58，u=3.778 40，u/a=-19.123 7，z（0）（1）=1， 由此得出馬尾松毛蟲2 代幼蟲蟲口數的GM（1,1）災變預測模型：

將根據馬尾松毛蟲2 代幼蟲蟲口數的GM（1,1）災變預測模型得到的擬合值、 誤差等列于表4。

對觀察值和擬合值的差異進行t檢驗，t=0.195 2，df=20 時，t0.05=2.09，t＜t0.05， 兩者差異不顯著， 平均誤差只占觀察值均數的5.4%。 實際觀察值與通過GM（1,1）災變預測模型得到的擬合值之間誤差較小，各災變年的精度平均為84.08%， 總體平均精度為94.09%。 由此可以通過這個模型求得未來5 個時刻的預測值， 用所建災變預測模型對未來馬尾松毛蟲2 代幼蟲災變年份進行預測z＾（0）（12）=z＾（1）（12）-z（1）（11）=31.704 2， 由原始序號得知， 最后一次災變是2011 年，z（0）（11）=23， 現預測下一次災變年的序號z＾（0）（12）=31.704 2， 即從2011 年馬尾松毛蟲2 代幼蟲災變年算起， 再過9 a 即2020 年為馬尾松毛蟲2 代幼蟲大發生年， 同理可預測之后年份z（t+1）=31.704 2，z（t+2）=38.629 8，z（t+3）=47.068 4，z（t+4）=57.350 3，z（t+5）=69.878 2。

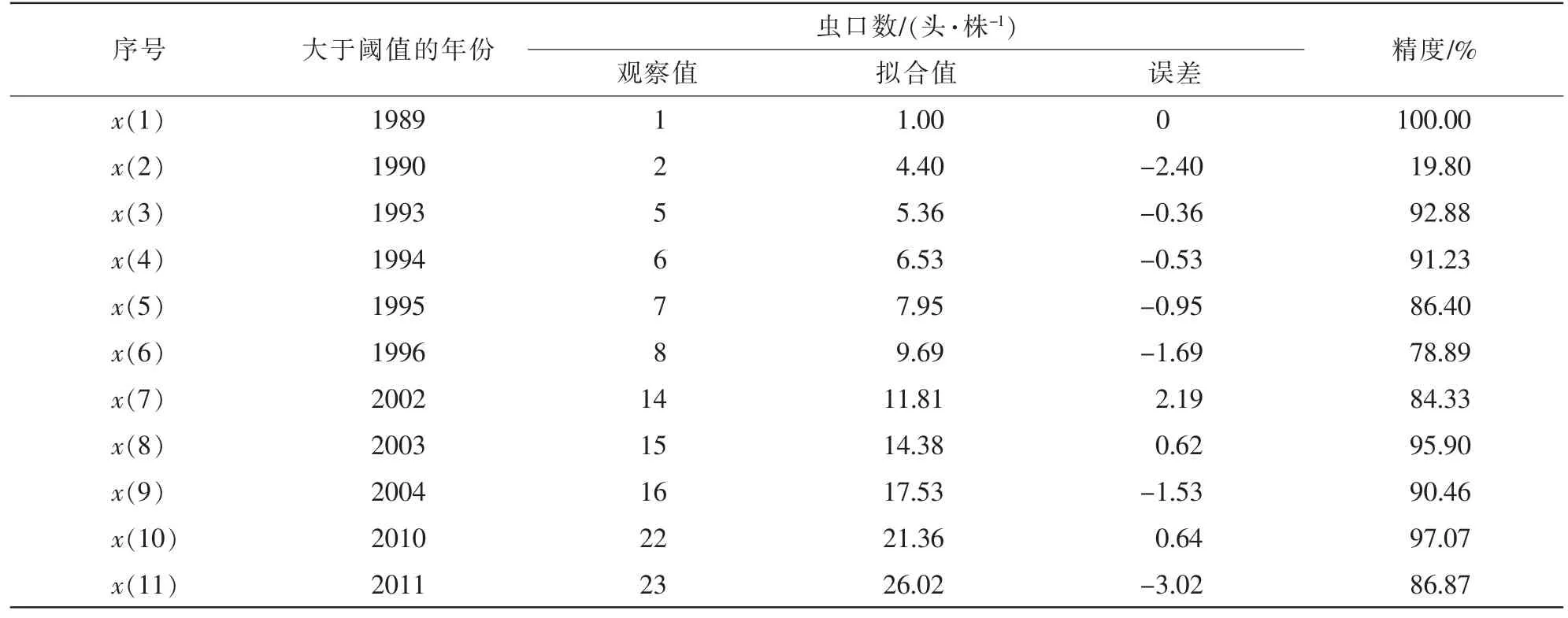
表4 馬尾松毛蟲2 代幼蟲蟲口數預測的擬合值與誤差Table 4 Fitting value and error of prediction of population number of second generation larvae of D. punctatus

3 小結與討論

利用灰色災變模型預測法對安徽省潛山縣1989-2016 年馬尾松毛蟲幼蟲越冬代、 1 代和2 代累計蟲口的災變進行預測， GM（1,1）災變預測模型分別是e0.24187k-17.181 8 和根據預測模型求得的已知年份的擬合值與觀察值進行t檢驗，t=0.101 7， 0.218 6 和0.195 2， 均小于t0.05， 差異均不顯著， 總體平均精度達96.25%、92.34%和94.09%， 各災變年精度平均值為84.40%、 84.85%和84.08%， 誤差極小。 說明災變預測法對馬尾松毛蟲幼蟲發生量災變的預測預報是一種較理想的預報方法。 從2011 年算起， 預測越冬代災變年為2021 年， 1 代災變年為2022 年， 2 代災變年為2020 年。

害蟲種群的消長， 其本質是害蟲種群與環境之間進行物質交換和能量傳遞的結果， 它既含有已知的信息， 又含有未知的或非確知的信息， 實際上是一個灰色系統。 灰色系統災變預測一般是指某種大于閾值的災害在哪一年份出現， 灰色系統災變預測已經運用到國民經濟各個方面的預測， 在植物保護方面也被大量利用。 在農業害蟲的預測上， 預測結果與實際情況吻合度很高［11-13］。 灰色系統災變預測結果在林業害蟲的預測上也有報道， 吳秋芳等［14］對河南省安陽縣楊樹Populus苗圃地下害蟲進行灰色災變預測，平均精度達90.40%。 宋丁權等［15］用灰色理論中的災變模型以及灰色區間模型對馬尾松毛蟲災級出現的年份進行了模擬、 預測和分析， 也取得了較好的效果。 與中國馬尾松毛蟲發生的其他省區相比， 安徽省馬尾松毛蟲發生的偶災區， 由于安徽省馬尾松林面積較大， 加之還有一定面積的濕地松和火炬松的純林和混交林， 為馬尾松毛蟲的猖獗提供了發生的基礎條件， 安徽省地處亞熱帶和溫帶的過渡帶， 溫、 濕、降雨等氣候條件均適宜于馬尾松毛蟲的發生， 馬尾松毛蟲發生的森林環境， 常災區絕大部分為海拔100～300 m 的丘陵地區， 偶災區為海拔300～500 m 的山區， 海拔500 m 以上的山區很少有馬尾松毛蟲發生， 安徽省為海拔400～800 m 的偶災區［1］。 馬尾松毛蟲在遇到適宜的發生條件， 極易爆發成災， 所以對馬尾松毛蟲猖獗成災的預報有著重要的意義。 本研究預測了安徽省潛山縣馬尾松毛蟲越冬代、 1 代和2代幼蟲發生的嚴重年份， 平均精度分別為96.25%、 92.34%和94.09%。 灰色災變模型預測法預測周期長， 預測結果精度高， 是較理想的預測方法。 對灰色災變模型的應用在原始序列數據中應有一定的時間長度， 這樣精度才能提高， 再者災變模型隨著時間的推移， 也需要不斷更新和修正。