基于機器學習算法的廣西桉樹適宜性研究

杜雨菲， 吳保國， 陳玉玲

（北京林業大學 信息學院， 北京100083）

桉樹Eucalyptus栽培是廣西林業生產發展中的優勢產業［1］。 作為短周期工業原料林首選的造林樹種之一， 桉樹效益高、 周期短， 但生長受立地條件影響較大， 規模栽培時需要進行適宜性研究。 樹種適宜性研究是當前開展適地適樹、 造林決策研究的熱點［2］。 王小明等［3］綜合了氣候、 土壤、 地形等環境因子建立Logistic 回歸模型用以確定香榧Torreya grandis‘Merrillii’ 適宜種植區域， 模型檢驗數據集的總正確率達到了69.8%。 KOO 等［4］基于環境因子， 建立物種分布模型和時間模擬模型研究云杉Picea rubens適生區， 模型驗證結果的曲線下面積（area under curve， AUC）達0.99。 胡秀等［5］基于溫度、 降雨及海拔等環境因子， 采用MaxEnt 模型軟件構建了檀香Sautalum album的適宜性預測模型， AUC 值為0.98。 高若楠等［6］選取立地因子， 利用隨機森林模型研究了杉木Cunninghamia lanceolata的適宜性， 模型泛化精度達89.5%。 PIRI-SAHRAGARD 等［7］利用隨機森林模型分別探討了環境因子與白梭梭Haloxylon persicum等5 種植物分布之間的關系， AUC 值總體在0.95 以上。 相較于傳統數學建模技術， 物種分布模型和機器學習模型在構建樹種適宜性評價模型時效果較好。 目前， 應用于樹種適宜性研究的機器學習分類算法層出不窮， 但通過對比分析多種不同的分類算法， 從而進行樹種適宜性評價的研究相對較少。 本研究以廣西桉樹為對象， 使用樸素貝葉斯（naive bayesian， NB）［8］、 支持向量機（support vector machine， SVM）［9］、隨機森林（random forest， RF）［10］等3 種機器學習分類算法， 探索立地因子與桉樹適宜性之間的關系， 開展樹種適宜性研究， 為桉樹適宜性研究提供新思路， 為科學造林提供支持。

1 材料與方法

1.1 研究區概況

研究區廣西國有高峰林場（22°49′～23°15′N， 108°08′～108°53′E）地處廣西壯族自治區南寧市， 屬低丘陵山地地帶， 平均海拔為200～500 m。 亞熱帶季風氣候， 年平均氣溫為20.8～21.9 ℃， 年均相對濕度80%以上。 海拔300 m 以下的土壤絕大部分為赤紅壤［11］。 地理位置、 氣候和土壤條件均十分優越， 有利于亞熱帶植物的規模化種植。

1.2 數據來源

數據來源于廣西高峰林場森林資源規劃設計調查數據中的桉樹小班數據， 包括立地因子、 林分平均年齡、 優勢木平均高。 立地因子包括地貌類型、 海拔、 坡向、 坡位、 坡度、 凋落物厚度、 腐殖質層厚度、 土層厚度、 石礫含量、 成土母質和土壤類型。 地貌類型有低山、 丘陵2 種， 坡向包括東、 南、 西、北、 東北、 東南、 西北、 西南、 無坡向， 坡位包括脊部、 上坡、 中坡、 下坡、 谷地、 平地， 成土母質包括砂巖、 第四紀紅土， 土壤類型包括赤紅壤、 黃壤、 紅壤。 整理數據， 剔除缺失嚴重記錄、 異常數據，得到桉樹小班數據1 883 個。

1.3 研究方法

1.3.1 樸素貝葉斯算法 樸素貝葉斯算法是一種基于概率論的機器學習分類算法［8］。 針對桉樹小班數據訓練集D， 類別集合為yj，y1代表適宜桉樹生長，y2代表不適宜桉樹生長，ai是待分類的小班， 有a1，a2， …，a11共11 個立地因子。 統計在各類別下各立地因子的條件概率估計值， 即估計第i個立地因子在第j個類別中出現的概率P（ai∣yj）， 根據特征獨立性假設以及貝葉斯定理， 桉樹適宜性分類結果（hnb）可用樸素貝葉斯分類器表示為：

1.3.2 支持向量機算法 支持向量機是一種二分類機器學習算法［12］。 在由立地因子構成的特征空間中尋找1 個分類超平面對桉樹小班數據訓練樣本進行歸類（適宜或不適宜）， 分類超平面遵循間隔最大化原則。 設有2 類線性可分的樣本集合（gi，hi），i=1， …，n；hi∈{+1， -1}； 線性判別函數表示為：

式（2）中： ω 為平面的法向量，b為截距。 通過最大化間隔， 得到最優分類面函數式（3）。 對線性不可分的數據， 也可以通過核函數將其映射到高維空間， 使得樣本線性可分。

式（3）中：a*i是不為零的樣本， 即支持向量，b*是分類闕值。

1.3.3 隨機森林算法 隨機森林是一種集成機器學習算法［13］。 采用Bootstrap 重抽樣法對桉樹小班數據訓練集D 進行n次抽樣， 得到D1、 D2、 …、 Dn共n個訓練子集； 各訓練子集分別訓練1 棵決策樹， 組成隨機森林。 在單棵樹的訓練過程中， 隨機選出部分立地因子用以確定決策樹的分割節點， 得到n種結果； 使用簡單投票法， 得到最多票數的類別或者類別之一為最終的桉樹適宜性評價模型， 輸出結果見式（4）。

式（4）中：H（x）為組合分類模型；hi（x）為單個決策樹分類模型；Y為輸出桉樹適宜性的變量；I（ ）為示性函數。

1.3.4 模型評價指標 混淆矩陣（confusion matrix）也稱誤差矩陣（error matrix）， 是評價模型分類效果的常用的指標［14］。 如表1 所示： 混淆矩陣的每一列代表了桉樹適宜性評價模型的預測類別， 每一行代表該小班真實的歸屬類別， 主對角線元素的總和為被正確分類的小班總數（N）。 模型的精度（A， 包括擬合精度和泛化精度）可用小班數與小班總數的比值來表示：

式（5）中：NTP為正類預測為正類的小班數；NTN為負類預測為負類的小班數。 分類誤差率（classification error rate）為該類別預測錯誤的小班數與該類別小班總數的比值， 包括模型對于桉樹生長適宜性的分類誤差率［式（6）］和不適宜性的分類誤差率［式（7）］。 精度、 生長適宜性的分類誤差率（ε1）和不適宜性的分類誤差率（ε2）通常作為衡量桉樹適宜性評價模型判定能力的指標［6］。

表1 混淆矩陣Table 1 Confusion matrix

式（6）和式（7）中：NFN為正類預測為負類的小班數；NFP為負類預測為正類的小班數。

2 結果與分析

2.1 模型實現

樹種適宜性評價標準最常用的是地位指數（site index， SI）［6］， 各小班地位指數可通過林分平均年齡和優勢木平均高得到［15］； 地位指數小于平均值的小班判定為不適宜桉樹生長， 大于或等于平均值的判定為適宜桉樹生長［6］。 本研究的1 883 個樣本數據中， 適宜桉樹生長的樣本有1 005 個， 不適宜的有878個， 樣本量存在一定的不平衡性。 利用機器學習算法解決分類問題時， 數據集不平衡會對模型效果造成影響， 因此需要進行平衡化處理。 在不損失原始樣本的前提下， 通過SMOTE 算法［16］對樣本構成做平衡化處理， 共得到樣本量3 512 個， 其中適宜桉樹生長的樣本1 756 個， 不適宜的1 756 個； 將實驗數據按70%和30%的比例分為訓練樣本和測試樣本， 分別用于模型的訓練和測試。

使用naiveBayes（ ）函數構建樸素貝葉斯模型、 svm（ ）函數構建支持向量機模型、 randomForest（ ）函數構建隨機森林模型。 3 種模型的輸入均為地貌類型、 海拔、 坡向、 坡位、 坡度、 凋落物厚度、 腐殖質層厚度、 土層厚度、 石礫含量、 成土母質， 土壤類型， 輸出均為桉樹生長適宜性。 利用模型評價指標對比不同模型， 取最優模型確定為桉樹適宜性評價模型并進行桉樹生長適宜性預測。 對給定立地因子的小班， 將立地因子輸入選取的模型， 輸出該小班適宜桉樹生長的概率， 判斷該小班是否適宜桉樹生長。 進行立地因子重要性評估， 分析立地因子對桉樹生長的影響， 得出適宜桉樹生長的立地條件。 桉樹適宜性預測模型構建流程如圖1 所示。

2.2 模型精度分析

多次訓練發現： 樸素貝葉斯、 支持向量機、 隨機森林算法構建的桉樹適宜性評價模型誤差變化均較穩定， 混淆矩陣（表2）擬合精度為63.18%、 69.73%和78.03%， 使用測試數據集對模型進行檢驗， 混淆矩陣泛化精度分別為64.33%、 67.93%和78.18%。 與樸素貝葉斯、 支持向量機算法相比， 隨機森林算法預測精度更高， 可作為桉樹適宜性評價的模型。

表2 3 種模型混淆矩陣Table 2 Partial correlation coefficient and its significance test

2.3 桉樹適宜性預測

利用隨機森林算法構建桉樹適宜性評價模型并對桉樹進行生長適宜性預測， 預測數據為廣西桉樹固定樣地數據， 各樣地的地位指數可通過查閱地位指數表得到［15］。 該數據中桉樹的地位指數的平均值為15.09， 將地位指數小于平均值的樣地判定為不適宜桉樹生長； 將地位指數大于或等于平均值的樣地判定為適宜桉樹生長。 隨機選取5 個樣本進行模型驗證， 將立地因子輸入模型， 輸出桉樹適宜性概率及適宜性判斷結果； 通過與地位指數的比對（表3）可知： 本研究使用隨機森林算法構建的桉樹適宜性評價模型在實際中是可以使用的。

圖1 模型構建流程圖Figure 1 Flowchart of model building

表3 隨機森林算法模型判斷結果Table 3 Predicted results of random forest models

2.4 立地因子重要性評估

利用隨機森林算法對立地因子進行重要性評估［10］。 對某個立地因子j隨機取值， 通過評估桉樹適宜性評價模型分類準確性下降的程度來評估j的重要性， 分類準確性下降程度越大， 說明j越為重要。 計算方法如公式（8）所示：

式（8）中：Ejr為j的值隨機后的袋外（out of bag， OOB）誤差，Er為j的值隨機前的OOB 誤差，NT為分類樹的數量。 標準化處理后得到的平均準確度降低程度（mean decrease accuracy， MDA）可用來描述立地因子j的重要性。

對分類樹節點作t分割， 計算使用立地因子j前與使用后基尼指數的減小值（DGj）， 對所有節點的DGj求和后再對所有分類樹NT取平均， 得到平均基尼指數降低程度（mean decrease Gini， MDG）。 MDG 越大， 立地因子j越重要。 基尼指數Gini（t）的計算方法如公式（9）所示。

式（9）中：p（i∣t）為類別i在節點t處的概率，k為分類結果數， 在本研究中取值為2。

使用varImpPlot（ ）函數對11 個立地因子進行重要性評估。 由表4 可知： 不同重要性評估方法對立地因子的排序結果基本一致； 立地因子的重要性排序由高到低依次為： 海拔、 土層厚度、 坡向、 坡度、石礫含量、 凋落物厚度、 坡位、 腐殖質層厚度、 土壤類型、 地貌類型、 成土母質。

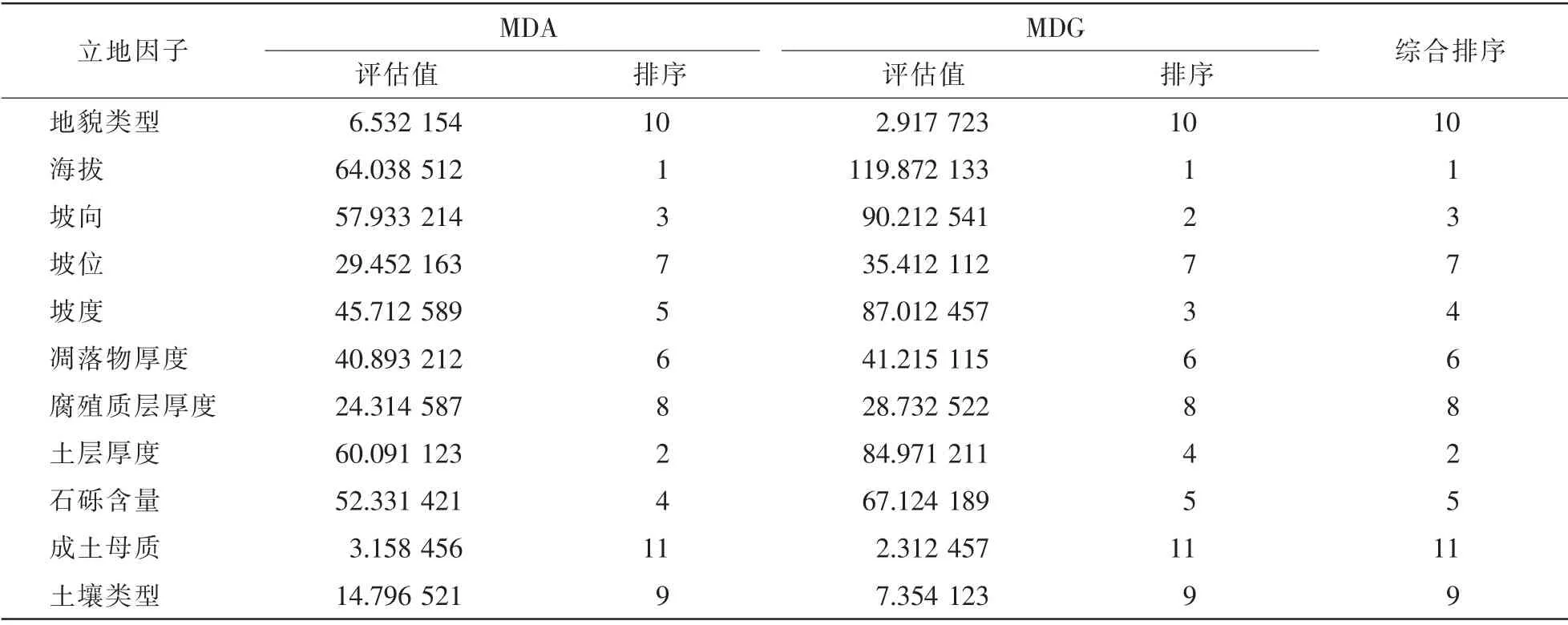
表4 立地因子重要性評估Table 4 Importance assessment of site factors

選取對桉樹生長影響最大的2 個立地因子（海拔和土層厚度）， 利用隨機森林算法進行單因素分析。由圖2 可知： 研究區海拔為200～350 m、 土層厚度為80～100 cm 的地區比較適合桉樹生長。

圖2 海拔、 土層厚度對桉樹生長的影響Figure 2 Effects of altitude and soil thickness on growth of Eucalyptus

3 結論與討論

基于樸素貝葉斯算法、 支持向量機算法、 隨機森林算法3 種算法構建的模型擬合精度分別為63.18%、 69.73%和78.03%， 泛化精度分別為64.33%、 67.93%和78.18%； 相較于樸素貝葉斯、 支持向量機算法， 隨機森林算法對缺失數據不敏感， 在訓練的過程中能檢測到特征與特征之間的互相影響， 模型泛化能力強， 具有更高的預測精度， 在本研究中分類效果最好。 缺少特征獨立性假設和立地因子數據是樸素貝葉斯算法分類效果差的原因； 而缺少通用的解決方案， 對缺失數據敏感， 受核函數的影響較大等導致了支持向量機算法分類效果欠理想。 本研究采用的多模型對比為以后其他樹種適宜性研究選取模型提供了參考。

海拔、 土層厚度、 坡向、 坡度等立地因子對桉樹生長影響較大， 地貌類型、 成土母質等則較小。 原因可能是海拔高度、 坡向、 坡度的改變造成空氣溫度、 空氣濕度、 太陽輻射等變化［6］， 從而影響桉樹生長； 土層厚度與土壤養分、 礦元素等密切相關［17］， 研究區的桉樹種植區域， 地貌類型和成土母質均比較單一， 因此對桉樹生長的影響并不明顯。 對海拔、 土層厚度等立地因子的單因素分析發現： 桉樹適宜生長地區多數海拔為200～350 m， 土層厚度為80～100 cm。 研究認為［18］： 海拔高度低于350 m， 桉樹徑生長隨海拔升高而增粗， 當海拔大于350 m， 環境熱量不足桉樹容易引發低溫凍害［19］。 土層厚度對桉樹的影響體現在土壤的營養狀況和給樹木生長提供的養分上［17］， 本研究發現土層越厚， 土壤營養條件越好，也越適宜桉樹生長。 總的來說， 不同的立地因子對桉樹生長的影響程度不同， 選擇桉樹種植區域時應客觀考慮各個立地因子的影響程度， 從而合理地調整立地條件的組合， 最大程度滿足桉樹生長。

基于機器學習算法構建的樹桉樹適宜性評價模型可以較好地對桉樹的適宜性做出預測， 為科學造林提供依據。 樹種適宜性分析不僅要將立地分為適宜該樹種生長以及不適宜該樹種生長， 還可以進一步對其進行細分， 從二分類問題轉變為多分類問題， 進一步研究機器學習算法在樹種適宜性分析中的應用。