觀三線 抓特點 辨八角
趙連杰
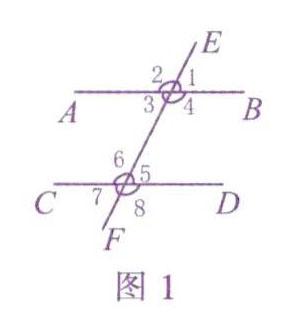

兩條直線被第三條直線所截.構成了八個角,我們習慣上稱之為“三線.八角”.
如圖l所示,其中沒有公共頂點的角可分為三類,即同位角、內錯角、同旁內角,它們是進一步學習平行線的判定和性質的重要基礎,是學好本章的關鍵所在.但因這三個概念近似,同學們辨別起來有很大困難,經常出現這樣那樣的錯誤.現對辨別這三個概念的步驟說明如下,希望對同學們有所啟示,
第一步:確定截線與被截線
辨別“三線八角”的關鍵是確定哪兩條直線被哪一條直線所截,為此首先要分清兩條直線和第三條直線,為了直觀簡便,可以將兩條直線稱為被截線,將第三條直線稱為截線,截線是被截兩條直線的橋梁.確定它們的方法為:待確定的兩個角分別有一條邊在同一條直線上,那么這條直線就是截線,兩個角另外兩條邊所在的兩條直線就是被截線,或者說,截線是同位角、內錯角或同旁內角中兩個角的一邊所在的公共直線,兩條被截線是同位角、內錯角或同旁內角中兩個角的另一條邊所在直線.
第二步:抓住每個概念的特征
1.同位角要抓住一個“同”字,即“位置相同”,其意思是兩個角都在截線的同旁和兩條被截線的同方向(同上或同下,同左或同右).
2.內錯角要抓住“內”字和“錯”字,即夾在兩條被截線之間和位于截線的兩旁,形同“Z”.
3.同旁內角要抓住“同”字和“內”字,即夾在兩條被截線之間和位于截線的同旁,形同“U”.
第三步:準確得出結論
結合圖形,根據第一步的方法確定截線和被截線后,根據第二步中各個概念的特點(主要就是看要判斷的角與前面確定的截線和被截線的位置關系),給出結論,對于比較復雜的圖形,要善于將圖形分解,即根據自己所思考的問題,抽出只與所考察的角有關的直線或線段,去掉那些與問題無關的直線或線段(也就是留下第一步確定的相關的兩條被截線和一條截線),從而得到正確的結論.
幾個應該特別注意的事項:
1.三類角反映的是角與角之間的位置關系而不是數量關系,因此,不論被截的兩條直線是否平行,都存在上述三類角.
2.對于比較復雜的圖形,可以用不同顏色的筆將所找到的截線和被截線描出來,然后再辨別是哪一類角.
3.注意與前邊學過的對頂角、鄰補角的區別,這三類角沒有公共頂點.
例l 如圖2所示.∠B和∠FAC是哪類角?∠B和∠C呢?
解析:8 ∠B的兩邊分別在直線AB,BC上,∠FAC的兩邊分別在直線AB,AC上,所以AB為截線,BC,AC為被截線,∠和∠FAC都在截線AB的同旁和被截的兩直線BC,AC的同方向(上方),由此便知∠B和∠FAC為同位角.
∠B的兩邊分別在直線AB,BC上,∠C的兩邊分別在直線BC,AC上,所以BC為截線,AB,AC為被截線,∠B和∠C都在截線BC的同旁和被截的兩直線AB,AC之間,由此便知∠B和∠C為同旁內角,
練一練
1.如圖3所示,下列說法錯誤的是(? ).
A.∠l與∠A是同旁內角
B.∠3與∠A是同位角
C. ∠2與∠3是同位角
D.∠3與∠B是內錯角
2.下列四個圖形中,∠1與∠2為同位角的是(? ).
參考答案:1.B 2.D

