基于量子粒子群算法的大型陣稀疏優化方法
郭玉霞 張艷艷 邢金鳳 袁曉壘
摘要:本文提出了一種基于量子粒子群算法(quantum particle swarm optimization,QPSO)的大型陣稀疏優化方法。該方法在約束主瓣寬度的條件下,以陣列的陣元位置和節點的相位中心為優化參量,以方向圖的峰值副瓣電平為優化目標,有效結合了QPSO算法,并將其應用于大型陣的稀疏優化。相對于傳統稀疏優化方法,本文所提方法不受更新速度和軌跡的約束,并提高了全局搜索能力、加快了收斂速度。仿真結果驗證了該方法的有效性。
關鍵詞:QPSO;陣元位置;相位中心;峰值副瓣電平;稀疏優化
中圖分類號:TJ文獻標識碼:ADOI:10.19452/j.issn1007-5453.2020.08.009
大型、超大型相控陣列由于具有高增益、指向性強等優點得到越來越廣泛的應用,但滿陣形式的大型相控陣列需要龐大的饋電網絡和發射、接收通道,導致其具有高成本、低實時性等缺點。對此,陣列天線稀疏布陣技術應運而生,該技術是指從線陣或面陣中去掉一些天線單元,通過優化稀疏布陣,可改善陣列天線的輻射特性,實現陣列天線的方向圖綜合,以最少的單元數達到技術指標(如波束寬度)要求,在技術指標和天線造價之間達到一種折中[1]。
在過去幾十年中,陣列天線稀疏布陣研究一直是一項重要且有意義的工作。目前,用于稀疏優化的算法主要有遺傳算法[2]、粒子群算法[3]和模擬退火算法[4]等,每種算法更替解粒子的方法不同,最終導致優化速度也不同。因此,一般選擇采用哪種優化算法,除了取決于該算法是否適合實際應用外,主要考慮的因素就是優化速度。
本文提出一種基于量子粒子群算法(quantum particle swarm optimization,QPSO)的大型陣稀疏優化方法。QPSO是Sun等從量子力學出發提出的一種新粒子群算法[5]。QPSO算法相對于粒子群算法(PSO)具有進化方程簡單、控制參數少、收斂速度快和運算簡單等優點,在測試函數和很多實際應用中都取得了優于PSO算法的效果。
1建立優化陣列模型
首先,定義本文優化時采用的參考坐標系如圖1所示,其中?和θ是方位角和俯仰角,本文之后的仿真試驗與理論分析均沿用圖1的坐標系。
1.1優化陣元位置
為論述基于QPSO算法的面陣稀疏優化陣元位置方法,本文以23行23列的八邊形面陣為例建立天線陣元位置模型,該八邊形陣列由23×23個天線陣元構成的矩形平面陣切掉4個角之后得到。頻率F0=15GHz、陣元間距取半波長,陣元數為373,如圖2所示。


3仿真試驗及性能分析
3.1試驗一
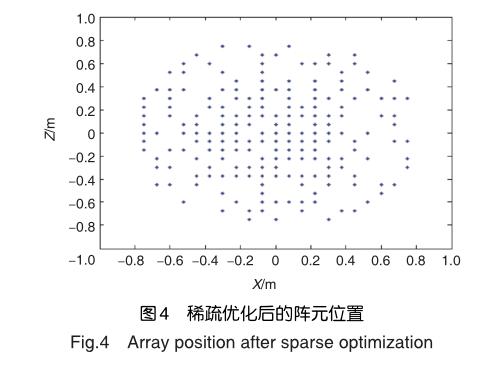
以373-面陣為稀疏優化模型,稀疏率設為sparse=0.52,設置QPSO算法的基本參數:迭代次數60,種群規模300。稀疏優化結果:(1)稀疏后所得陣元總數為194≈0.52×373,圖4是稀疏優化后373-面陣的陣元位置;(2)掃描范圍( -60°,60°),最大副瓣電平為-24.26dB,主瓣寬度7.6°,圖5、圖6是稀疏優化后的歸一化方向圖,與滿陣方向圖相比降低7dB;(3)圖7是QPSO算法應用于373-面陣稀疏優化后的收斂曲線。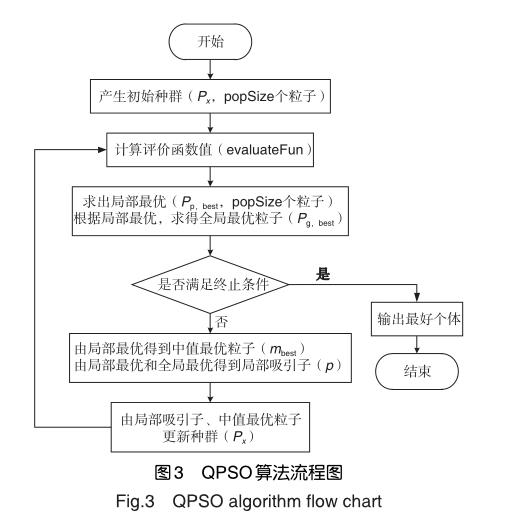

3.2試驗二
為進一步說明QPSO算法應用于平面陣稀疏優化的優勢,表1是在隨機選擇稀疏率條件下,稀疏優化后的陣列的歸一化方向圖的峰值副瓣電平PSLL值。從表中可以看出,稀疏率接近0.5時,副瓣電平接近最低。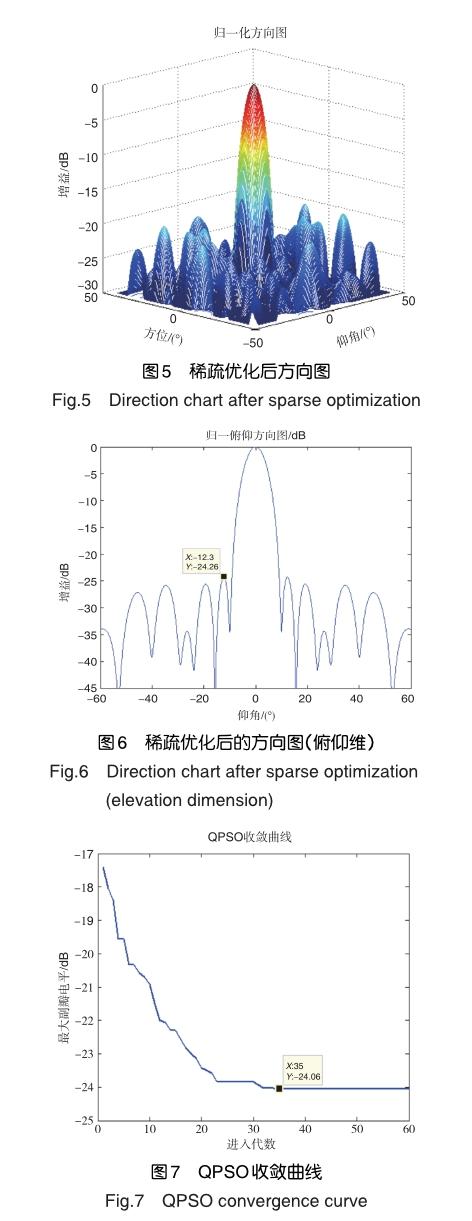
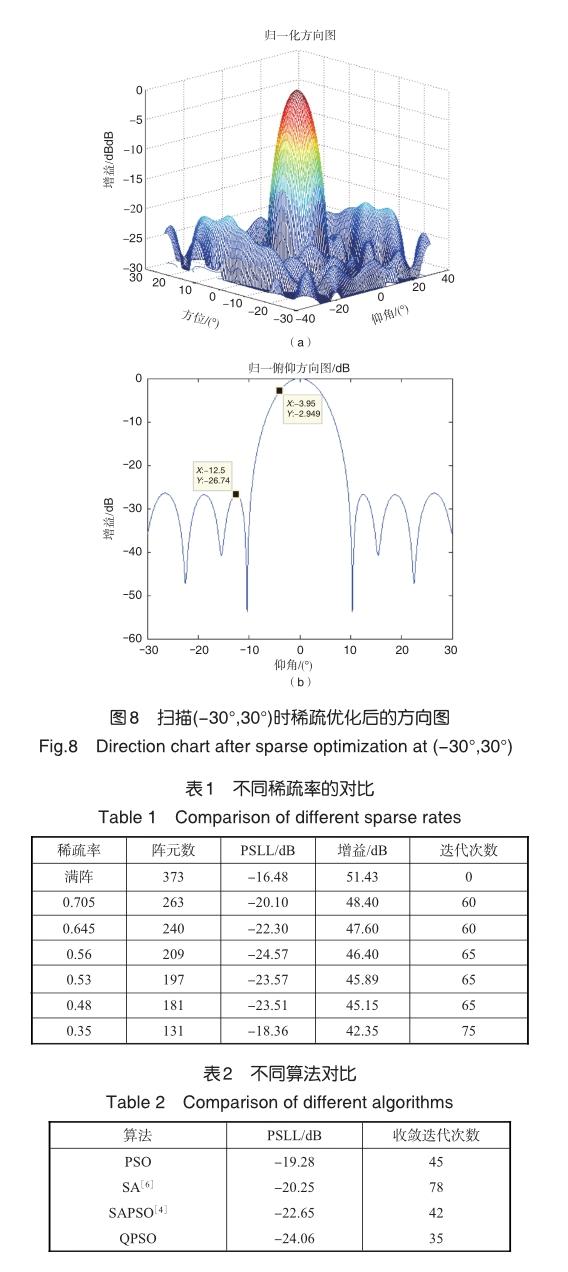
表2給出了不同算法應用于面陣優化的結果,對比而言,本文提出的基于QPSO算法稀疏優化面陣的方法相比于粒子群算法得到的稀疏陣的峰值旁瓣電平降低了4.78dB;與參考文獻[6]中采用模擬退火算法得到的稀疏陣的峰值旁瓣電平相比降低了3.81dB;與參考文獻[4]中采用模擬退火粒子群算法得到的稀疏陣的峰值旁瓣電平相比降低了1.41dB。從峰值旁瓣電平收斂迭代次數上看,相比于其他三種算法,QPSO算法在得到更低的峰值旁瓣電平的同時,收斂速度更快。
表3給出了相同情況下不同算法應用于373-面陣優化的結果,使用相同的設備分別用三種優化算法對373-面陣進行稀疏優化,掃描范圍一致。對比而言,本文的QPSO算法在增益損失不大的同時,峰值旁瓣電平更低,優化速度更快[13-15]。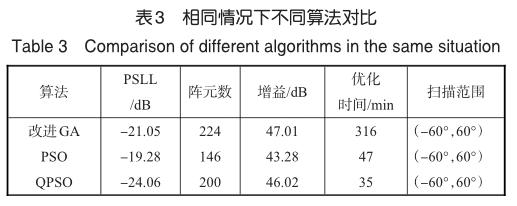
3.3試驗三
以上仿真均是確定稀疏率的情況下得到的結果,為了進一步說明QPSO算法的有效性,在不確定稀疏率的模式下稀疏優化373-面陣,圖9是13次QPSO算法后的收斂曲線疊加圖,并給出13次收斂曲線的平均曲線。
由收斂曲線疊加圖分析得,QPSO算法應用于373-面陣稀疏優化后,平均副瓣電平是-23.96dB,平均迭代次數52。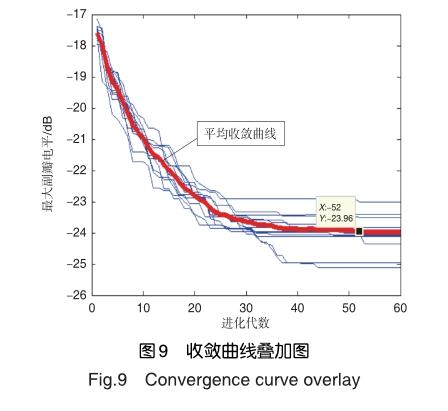
4結論
本文將QPSO算法應用于平面陣的稀疏優化陣元位置和稀疏優化節點相位中心問題。通過仿真試驗以及與已有文獻上的算例的比較,說明了QPSO算法應用于大型陣稀疏優化方法的優越性,并表明了QPSO算法應用于陣型優化的有效性。
參考文獻
[1]陳定,李建新.稀疏陣的最優化設計[J].微波學報, 2010(s2): 204-206. Chen Ding, Li Jianxin. The optimal design of the sparse array[J]. Journal of Microwaves, 2010(s2): 204-206.(in Chinese)
[2]孫晨偉.大型陣列的降維優化波束形成[D].西安:西安電子科技大學, 2013. Sun Chenwei. The dimension reduction of large arrays optimizes beam formation[D]. Xian:Xidian University, 2013.(in Chinese)
[3]Mandal D,Kar R,Ghoshal S P. Thinned concentric circular array antenna synthesis using particle swarm optimization with constriction factor and inertia weight approach[C]// Research and Development. IEEE,2011:194-198.
[4]王倩,王布宏,李龍軍,等.模擬退火粒子群算法的同心陣稀疏優化設計[J].空軍工程大學學報(自然科學版), 2015, 16(6):42-45. Wang Qian, Wang Buhong, Li Longjun, et al. Simulation of the annealingparticlegroupalgorithmsconcentricsparse optimization design[J]. Journal of Air Force Engineering University (Natural Science Edition), 2015, 16 (6): 42-45.(in Chinese)
[5]Sun J, Feng B, Xu W. Particle swarm optimization with particles having quantum behavior[C]// Congress on Evolutionary Computation, CEC2004. IEEE, 2004.
[6]廖先華,楊建紅,張立軍,等.基于模擬退火算法的平面稀疏陣優化[J].現代雷達, 2012, 34(10):57-59. Liao Xianhua, Yang Jianhong, Zhang Lijun, et al. Plane sparse array optimization based on simulating annealing algorithm [J]. Modern Radar, 2012, 34 (10): 57-59.(in Chinese)
[7]紀震.粒子群算法及應用[M].北京:科學出版社, 2009. Ji Zhen. Particle group algorithms and applications [M]. Beijing: Science Press, 2009.(in Chinese)
[8]劉鎧誠,何光宇,黃良毅,等.基于非對稱勢阱的量子粒子群算法及其應用[J].電網技術, 2016, 40(2):363-368. Liu Kaicheng, He Guangyu, Huang Liangyi, et al. Quantum particle group algorithm based on asymmetric potential trap and its application[J]. Power System Technology, 2016, 40 (2):363-368.(in Chinese)
[9]Yang S,Wang M,Jiao L. A quantum particle swarm optimization[C]//Proceeding of the 2004 IEEE Congress on Evolutionary Computation,2004.
[10]張凱,肖建華,耿修堂,等.基于漢明距離的DNA編碼約束研究[J].計算機工程與應用, 2008, 44(14):24-26. Zhang Kai, Xiao Jianhua, Geng Xiutang, et al. Research on DNA coding constraints based on Hanming distance[J]. Computer Engineering and Applications, 2008, 44 (14): 24-26.(in Chinese)
[11]張濤,史蘇怡,徐雪琴.基于二進制量子粒子群算法的含分布式電源配電網重構[J].電力系統保護與控制, 2016(4):22-28. Zhang Tao, Shi Suyi, Xu Xueqin. Refactoring of distributed power distribution networks based on binary quantum particle group algorithm[J]. Power System Protection and Control, 2016 (4): 22-28.(in Chinese)
[12]奚茂龍,孫俊,吳勇.一種二進制編碼的量子粒子群優化算法[J].控制與決策, 2010, 25(1):99-104. Xi Maolong, Sun Jun, Wu Yong. A binary-coded quantum particle group optimization algorithm[J]. Control and Decision, 2010, 25 (1): 99-104.(in Chinese)
[13]嚴韜,陳建文,鮑拯.基于改進遺傳算法的天波超視距雷達二維陣列稀疏優化設計[J].電子與信息學報, 2014, 36(12): 3014-3020. Yan Tao, Chen Jianwen, Bao Zheng. The sparse optimization design of the skywave super-view radar 2D array based on the improved genetic algorithm[J]. Journal of Electronics and Information Technology, 2014, 36 (12): 3014-3020.(in Chinese)
[14]樊會濤,閆俊.自主化:機載導彈重要的發展方向[J].航空兵器, 2019, 26(1): 1-10. Fan Huitao, Yan Jun. Autonomous:the important direction of development of airborne missiles[J]. Aero Weaponry, 2019, 26(1): 1-10.(in Chinese)
[15]王錚,韓寶玲.基于交互多模型的粒子濾波導引頭機動目標檢測技術研究[J].航空兵器, 2020, 27(1): 26-32. Wang Zheng, Han Baoling. Study on the detection technology of particle filter guide head maneuvering target based on interactive multi-model[J]. Aero Weaponry, 2020, 27 (1): 26-32.(in Chinese)(責任編輯陳東曉)
作者簡介
郭玉霞(1979-)女,碩士,研究員。主要研究方向:雷達導引信息處理技術。
Tel:13837993383
E-mail:ggyuxia@sina.com
Sparse Optimization Method for Large Arrays Based on Quantum Particle Swarm Optimization
Guo Yuxia1,2,*,Zhang Yanyan3,Xing Jinfeng3,Yuan Xiaolei1
1. China Aviation Missile Academy,Luoyang 471009,China
2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons,Luoyang 471009,China
3. Xidian University,Xian 710071,China
Abstract: In this paper, we propose a sparse optimization method for large arrays based on Quantum Particle Swarm Optimization (QPSO). Under the constraint of the main lobe width, this method takes the array element position and the node phase center as optimization parameters, and uses the peak side-lobe level of the pattern as the optimization target. It effectively combines the QPSO algorithm and will be applied for sparse optimization for large arrays. Compared with the traditional sparse optimization method, the method proposed in this paper is not restricted by the update speed and trajectory, and it improves the global search ability and accelerates the convergence speed. Simulation results verify the effectiveness of the method.
Key Words: QPSO; array position; phase center; peak side-lobe level; sparse optimization

