天津市設計暴雨雨型的演變

黃津輝，王 超，范澤華

(1.南開大學中加水與環境安全聯合研發中心，天津 300350；2.重慶交通大學河海學院，重慶 400074； 3.海綿金水(北京)工程設計院有限公司，北京 100089)

海綿城市概念的提出，改變了以往城市雨洪管理以峰值控制為主的設計理念，將城市雨洪管理從峰值管理轉向了徑流總量的管理和徑流過程的控制[1-2]。傳統的城市排水系統是根據設計暴雨的極值來設計的，而海綿城市的重要指標年徑流控制量和暴雨徑流的非點源污染控制，都是以特定時間段內“量”的管理為重點[3]。降雨的時程分布是降水量或者降雨強度在時間上的分配，表征的是降雨過程的變化，也稱作雨型。

早在20世紀40年代，蘇聯學者莫洛可夫等[4]就對雨型問題進行了研究，在分析了烏克蘭地區降水資料后，根據統計計算，劃分了7種模式雨型。1957年，Keifer等[5]根據降雨強度和歷時的關系提出了芝加哥雨型，該雨型對各種歷時的暴雨過程都適用。1980年，Yen等[6]提出了一種單峰型的三角形雨型，用于計算小流域排水區域的徑流。1967年，Huff[7]在研究美國伊里諾斯州的暴雨后，提出把降雨按雨峰出現位置劃分成4類，并利用無量綱累積過程來表示雨型。1975年，Pilgrim等[8]提出把雨峰設置在出現概率最大的時段上，然后將雨峰時段在總雨量中的比例取為各場降雨雨峰所占比例的均值，其他各時段的雨量比例也用相同的方法確定。我國對雨型的研究相對較少，2002年王家祁[9]提出“短推長”和“長包短”兩種雨型方法，這兩種方法在很大程度上避免了傳統以典型暴雨進行頻率放大作為設計雨型導致偶然性較大的不足。武晟[10]分析了王家祁雨型方法、三角形雨型和Pilgrim & Cordery雨型的適用性，指出相對于三角形雨型和Pilgrim & Cordery雨型，王家祁雨型更加符合當地實際情況。2011年范澤華[11]利用天津多年暴雨資料和Huff雨型方法給出了天津暴雨雨型的頻率分布特征。2018年李志元等[12]給出了多種暴雨雨型在降雨資料充分與否時的推薦方案。

雨型的差異不僅影響降雨的峰現時間，更影響降雨在研究流域中產生的徑流總量[13]，因此，對于工程設計的徑流計算，相應總雨量在降雨過程上的分配，不能簡單以一場典型降雨過程為標準，而應當基于當地大量的暴雨資料，在充分研究當地暴雨規律的基礎上，選擇具有統計規律的設計雨型。

在海綿城市建設的大趨勢下，對設計暴雨和設計雨型的研究要求逐漸提高，雖然目前已經有多種設計暴雨和設計雨型的方法，但關于設計暴雨和設計雨型在大型城市隨時間的演變規律的研究很少[14]。2013年黃津輝等[15]對天津市多種設計暴雨的方法進行了比較，發現現行的設計暴雨強度不同于根據1951—2004年暴雨數據推求的設計暴雨強度。2017年成丹等[16]利用同頻率法研究了宜昌市的設計暴雨雨型的演變特征，發現短歷時暴雨的峰值增加持續時間變長。由于防洪排澇水利工程設施等很多是百年工程的設計，設計暴雨和設計雨型等都是這些工程設計的標準[17]；對設計暴雨及雨型的不確定性和變化規律進行研究，在設計中就考慮降低風險的措施，對提高水利工程的韌性和長期性能具有重要意義[18-20]。

天津市位于京津冀都市經濟圈，是我國北方重要的經濟中心，總面積11 916.85 km2，城市建成區面積2 585 km2；截至2018年，總人口1 559.60萬人，是典型的超大城市。隨著城市快速發展，城市面積擴展迅速，這極大地改變了該地區的水文循環、水量平衡和能量平衡，城市開發的水文效應顯著。由于大城市人口密度大，公共和私人財產高度聚集，城市系統的脆弱性高，研究大型城市降雨統計規律，研究其設計暴雨和設計雨型，可為城市風險控制、城市規劃設計、城市建筑物和基礎設施建設等提供參考[21]。目前世界上對大城市暴雨雨型及雨型演變的研究不多，且不充分。天津市是位于北方沿海地區的大城市，對其雨型演變規律進行研究，有很強的典型性和借鑒意義，可為其他超大城市的建設和管理提供參考。

1 資料與方法

1.1 數據來源

本文所用暴雨資料來自天津市氣象局，為塘沽氣象站1951—2004年共54年的逐分鐘暴雨資料，是對天津市氣候監測站降水自記紙記錄進行信息化處理后得到的數據，每年選取前3場最大暴雨，共計162場暴雨資料。暴雨資料涵蓋年限長、樣本量大，降雨序列包含的暴雨極值代表全面，能夠較好地反映實際暴雨過程。

1.2 Huff雨型

1967年Huff[7]利用伊利諾斯州中東部的49個雨量站1955—1966年的降雨數據對降雨時程進行了分析，并根據降雨峰值出現在一場暴雨中時程區間的不同，將降雨時程分布劃分成4種降雨類型，降雨峰值出現在降雨歷時的第幾個四分之一時段，就稱為第幾四分之一雨型。研究表明，降雨峰值大多出現在前兩個四分之一區間內。1990年Huff[22]又利用伊利諾斯州其余12個雨量站和芝加哥地區的6個雨量站研究了點雨量和面雨量的時程分布，指出概率水平為50%的降雨過程最適合實際情況，峰現越早、峰值越高的暴雨時程分配對城市排水系統的壓力越大，風險越高。

1.2.1降雨場次劃分

本文根據天津市氣象局多年實測降雨分鐘記錄以及天津市的降雨特點，確定天津市的降雨時間間隔閾值P為12 h。如果降水量很小，則很難形成徑流，所以本文對用于推導雨型的場次雨量設置了閾值。參考中國氣象局對降雨強度等級劃分標準，設置場次降水量的閾值為2 mm。根據以上標準，對塘沽氣象站1951—2004年164次暴雨資料進行暴雨場次劃分，得到172場滿足標準的降雨，降雨歷時在3～50 h之間。

1.2.2Huff雨型推導方法

a. 總雨型。將172場降雨中的第n場的降水量記為Sn，xni表示第n場降雨中第i分鐘降水量；對第n場降雨按照降雨歷程進行十等分，每一段時間的降水量分別記為xn1、xn2、……、xn10。分別計算每一段時間內水量占總降水量的百分比，得到172場降雨每段降水量占總降水量的百分比；對每一段降水量百分比按照降序排列，然后按照經驗頻率計算排序后的頻率，分別提取10%、20%、……、90%對應的降水量占比。

b. 4類Huff雨型。根據降水量峰值出現時間在一場降雨歷時的位置，將降雨時程分布劃分為4種降雨類型(第一四分之一、第二四分之一、第三四分之一和第四四分之一雨型)。根據峰現時間把暴雨過程歸類后，重復總雨型的計算步驟即可得到不同類型的Huff雨型。

1.3 時段雨型計算

時段雨型的計算需要選取特定降雨歷時的降雨事件，根據總雨型的計算流程計算該降雨歷時下的雨型，即為某歷時的雨型。一般選用的時段雨型的降雨持續時間分別為1 h、3 h、6 h、12 h以及24 h。1 h 雨型是指根據降雨時間小于1h的降雨數據得到的雨型；3 h雨型是指根據降雨時間1～3 h的降雨數據得到的雨型；其他類推。時段雨型的計算方法參考總雨型的推導方式。

2 結果分析

2.1 天津市Huff雨型

根據Huff雨型推導方法，推求了天津市的Huff總雨型，如圖1所示。將降雨時間序列按雨峰出現位置的不同劃分成4類，對各類降雨進行歸類，進而得到各類雨型的平均無量綱累積過程。圖2為4種Huff雨型無量綱降雨時程分布累積曲線。由圖2可以看出，第一四分之一雨型和第二四分之一雨型差別較大，而第三四分之一雨型和第四四分之一雨型變化不明顯。概率水平為90%的曲線所表征暴雨的降雨時程分布雨峰相對其他頻率來講有滯后和平均化的趨勢，也是風險較小的時程分布形式。概率水平越小的暴雨過程，出現的概率越小，也越極端。從圖2可以看出，概率水平小的暴雨過程，其峰值出現的時間早，且峰值高，暴雨來的迅猛，所代表的暴雨雨型風險度大。從4種Huff雨型的各頻率降雨過程可以看出，概率水平為10%的降雨過程相對其他頻率的降雨過程累積降水量占比上升最快。

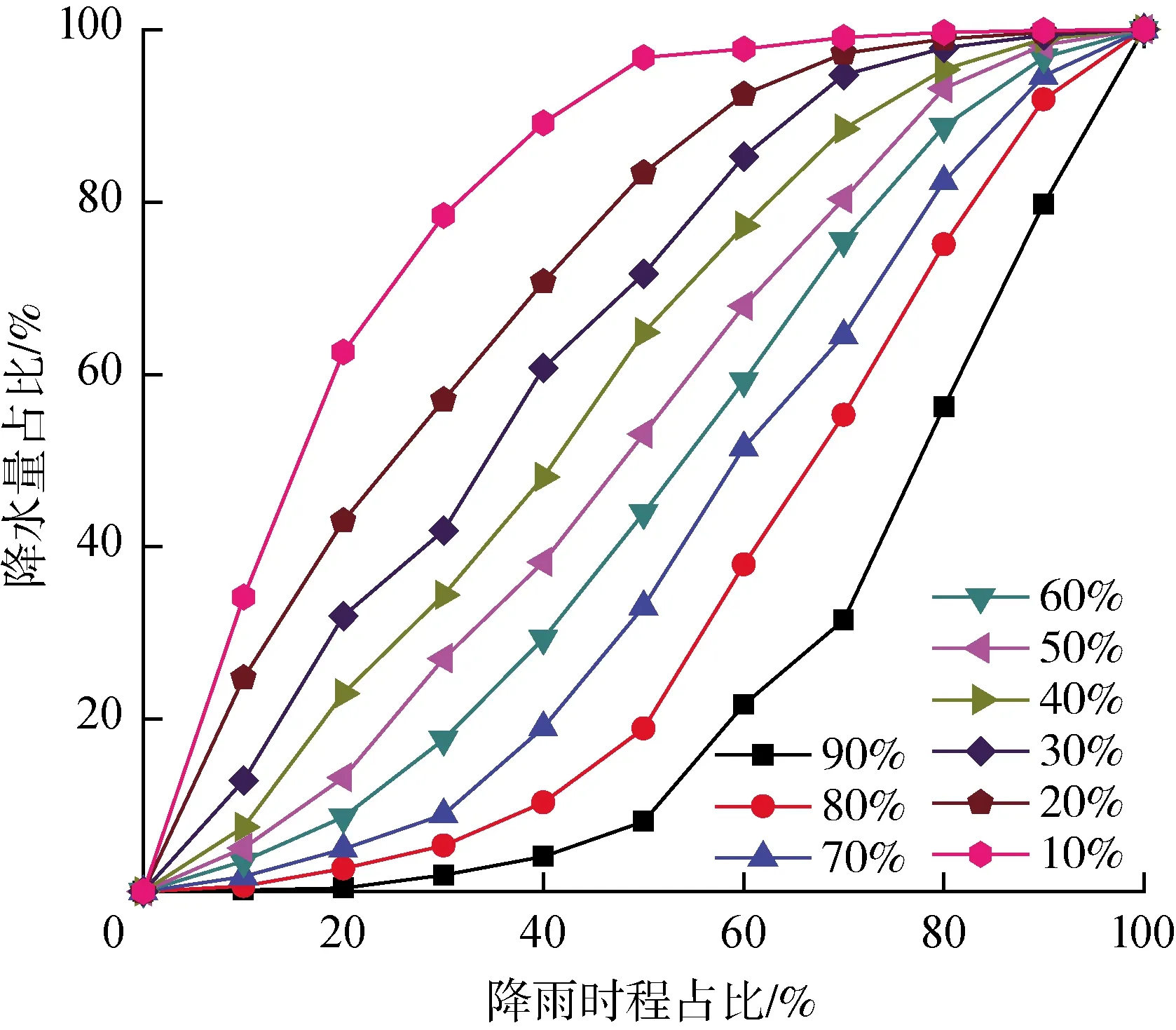
圖1 天津市Huff總雨型

(a) 第一四分之一雨型

(b) 第二四分之一雨型

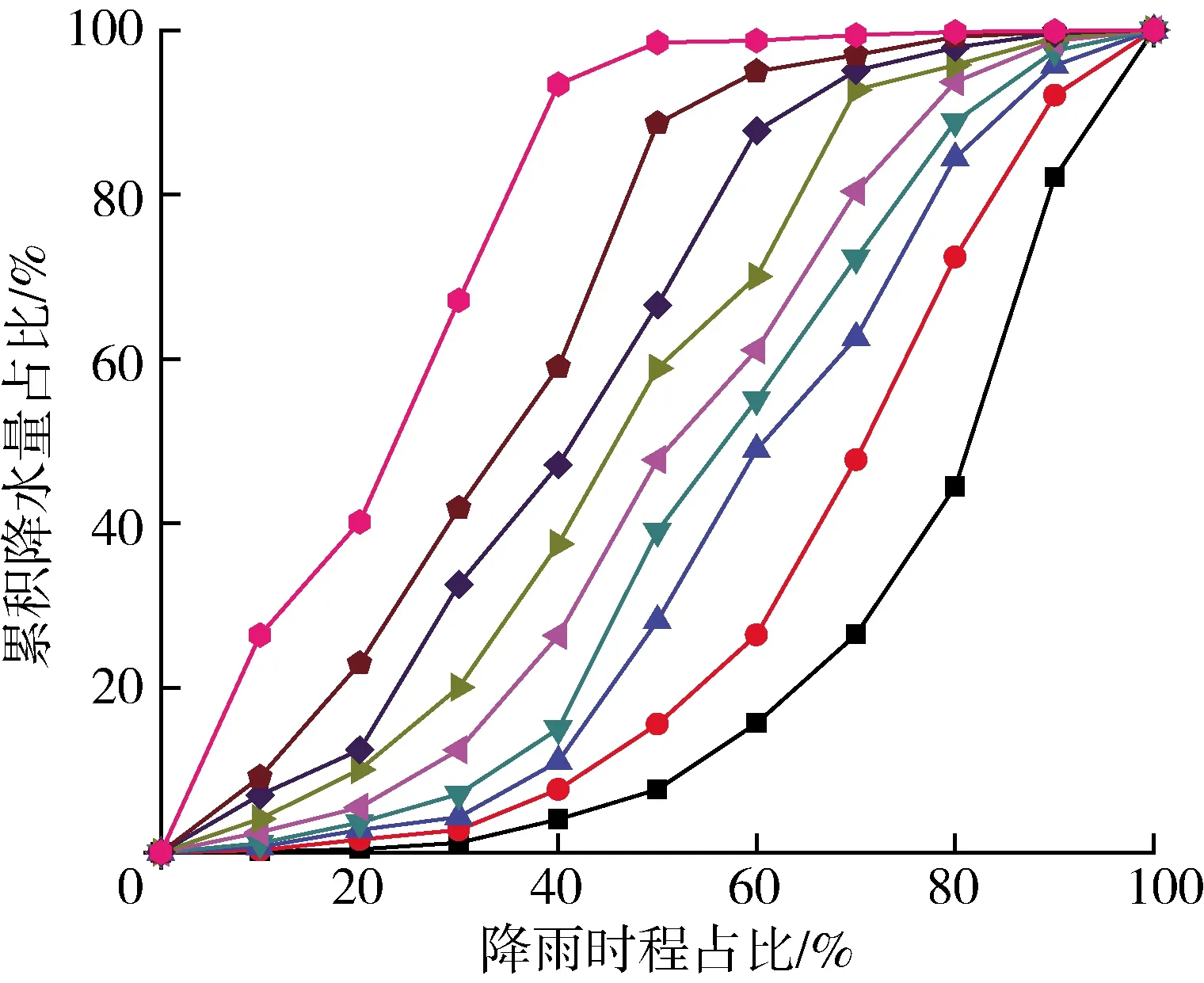
(c) 第三四分之一雨型

(d) 第四四分之一雨型

圖3是分別根據第一、第二、第三和第四四分之一雨型概率水平為50%的數據所繪制的無量綱累積降水量占比隨時程變化。從圖3可以看出，第一和第二四分之一雨型在降雨時程占比為50%時出現了交叉的現象。該現象表明，第一四分之一雨型的降水量分配在降雨時程的前期更為集中，而第二四分之一雨型在降雨時程的中后期其降水量比第一四分之一雨型的降水量要多。

圖3 第一、二、三、四四分之一雨型50%概率水平累積降水量占比

2.2 天津市時段Huff雨型

根據時段雨型的計算方法，分別計算了6 h、12 h、24 h的雨型，結果如圖4所示。從結果來看，概率水平為10%的累積降水量占比在降雨時程的前期升高最快，在降雨歷時的第一個四分之一時段內就達到了95%左右，說明概率水平為10%的降雨過程降水量主要集中在前期，而概率水平為90%的累積降水量占比增加速度最慢，累積降水量占比最晚到達100%。因此，相對而言，概率水平為10%的降雨過程對城市排水系統的壓力更大，更容易引起城市內澇。由于概率水平為10%的降雨過程峰現時間早，加之城市不透水面積大、降雨匯流速度快，使得雨峰有更大概率落在匯流時間內，或者使匯流時間內總降水量比其他頻率雨型的總降水量大，最終會導致更大的徑流量，增大城市排水系統的壓力，增加了城市內澇的風險。

2.3 天津市Huff雨型的年代際變化

為了直觀地分析比較天津市暴雨雨型的年代際變化，將天津市1951—2004年暴雨資料分為前 27年(1951—1977年)和后27年(1978—2004年)兩個時期，分別計算前后兩個時期的24 h雨型。對比前后兩個時期暴雨雨型的累積降水量占比后發現，除了概率水平為10%的24 h雨型變化不大，后27年雨型其他所有概率水平的24 h雨型前期降水量都增加，累積降水量占比隨降雨時程的增加速度更快。表1為各概率水平下前后兩個時期在第一個四分之一時段內的累積降水量占比，可以看到后27年在所有概率水平下第一個四分之一時段內的累積降水量占比都大于前27年。

(a) 6 h雨型

(b) 12 h雨型

(c) 24 h雨型

表2展示了天津市前后27年兩個時期概率水平為50%的6 h暴雨雨型降水量占比隨降雨時程分布情況。從表2可以看到，相對于前27年，后27年暴雨雨型發生了顯著的變化：首先，后27年暴雨雨型的雨峰出現在第40分鐘占總降水量的26.8%，而前27年暴雨雨型的雨峰則出現在第200分鐘占總降水量的15%，雨峰峰現時間大大提前；其次，在降雨歷時的前四分之一時段內前27年雨型的累積降水量占比為28.98%，而后27年雨型的累積降水量占比則達到了68.15%，說明降雨重心沿時程發生了顯著的提前；從表2可以看出前27年降雨資料獲得的雨型，其雨量分配比較均勻，而后27年雨型則呈現明顯的單峰型分布，降水量集中在降雨歷時的前期。總之，經過對比天津市前后兩個時期暴雨雨型的變化，發現后27年暴雨雨型在前期的降水量出現明顯增加，降雨峰值的出現時間明顯提前。天津市暴雨雨型的年代際變化說明，由于多種因素的影響，包括城市開發對水文效應的影響以及氣候變化的影響，暴雨的時程分布也在發生變化，因此在城市開發建設和海綿城市建設的推進工作中，應注意推求設計雨型所用暴雨資料的更新，方能獲得更符合當下特點的設計雨型。

表1 24 h雨型各概率水平下在第一個四分之一時段內累積降水量占比

表2 前后27年概率水平為50%的6 h暴雨雨型降水量占比隨降雨時程分布

2.4 雨型變化對徑流和年徑流總量控制率的影響

為了研究雨型發生變化情況下城市區域徑流量的響應情況，用總降水量為25.4 mm、不同時程分布的場次降雨來驗證同一個城市區域的產匯流情況。把2.3節中得到的天津市前后兩個時期概率水平為50%的6 h時段雨型作為兩個降雨方案，把兩種雨型的時程分布占比乘以一個固定的降水量(25.4 mm)生成兩種降雨時間序列方案(分別為前27年6 h設計暴雨雨型和后27年6 h設計暴雨雨型)。城市區域選擇天津濱海新區的一個面積為22.8 km2、不透水率為78.6%的成熟的開發區。圖5 是這個區域的SWMM模型，將區域分成了604個匯水分區，模擬了608個管道。在后27年6 h設計暴雨雨型下的徑流量峰值為42.01 m3/s，峰現時間為1:40，徑流總量為295.8×103m3。而在前27年6 h設計暴雨雨型下徑流峰值為42.91 m3/s，峰現時間為3:00，徑流總量為266.2×103m3。以上結果表明，在降水量相同的情況下，由于暴雨雨型的改變使雨峰提前，導致徑流的峰值相應提前了1 h 20 min,徑流總量也增加了。而暴雨徑流峰值的提前會縮短應對暴雨采取措施的時間，增加暴雨洪水的風險。

圖5 SWMM模型模擬的城市區域

3 結 論

a. 對天津市1951—2004年暴雨雨型的統計結果表明，天津市暴雨的大部分雨量集中在較短的時間內，且雨峰大多出現在第一個四分之一和第二個四分之一降雨時程內。

b. 相對于前27年，天津市后27年6 h雨型累積降水量占比增加更快，前期各概率水平下的累積降水量都要更高，前期降水量占比也更大，勢必增加城市徑流量，增大城市管網的壓力。

c. 天津市前后兩個時期的設計暴雨雨型發生了明顯的變化，受此影響，暴雨徑流過程的峰現時間提前，洪峰流量增長，徑流總量也相應增加。

d. 設計暴雨雨型不是一成不變的，天津市設計暴雨雨型發生了變化，使得雨峰前移、暴雨徑流峰值變大，城市管網排水壓力增大，從而增加了城市內澇的風險。因此，海綿城市規劃設計時應及時根據最新資料更新設計暴雨雨型，得到最符合當下情況的設計雨型，從而對海綿城市建設工作做出更有效的指導。