改進型格尼襟翼對不同實度的垂直軸風力機氣動性能的影響

朱海天，郝文星，李 春，丁勤衛

（上海理工大學 能源與動力工程學院，上海 200093）

近年來，垂直軸風力機（vertical axis wind turbine，VAWT）由于其造價低、運行噪聲小和適宜大型化等優勢成為了研究熱點［1-2］。然而，VAWT獲能效率較之水平軸風力機低［3-4］，因此亟待一種有效且價格低廉的裝置以改善VAWT 的氣動性能。

格尼襟翼（Gurney flap，GF）是一種安裝于翼型尾緣并垂直于弦線的平板。1978 年Liebeck［5］首次將GF 加裝于翼型，并驗證當GF 長度為1.25%c（c為弦長）時可極大地提升翼型氣動性能。隨后，經大量的相關實驗與數值模擬研究與分析可知，GF 具有增大升力和增強流動控制的效果［6-15］。隨著計算流體力學、實驗方法和主動流動控制的快速發展，GF 的作用機理和應用范圍得到了完善和擴大。Zhang 等［16］與Feng 等［17］將等離子激勵器與GF 相結合研究其流動控制效果。Lee［18-19］研究了具有孔陣的GF對翼型氣動性能的影響。Kinzel 等［20］研究了可擺動式GF 振蕩翼型的動態特性。Graham 等［21］通過實驗研究了GF 厚度對翼型氣動性能的影響。Cole 等［22］研究了不同翼型加裝GF 的增升效果。Ismail 等［23］與Shukla 等［24］將酒窩式翼型和GF 相結合以期增強GF 的流動控制效果。Xie 等［25］研究了GF對撲翼獲能效率的影響。

文獻[23-25]均對GF 應用于垂直軸風力機的發展做出了展望。因此，本文將GF 應用于垂直軸風力機并設計了一種改進型GF，通過數值模擬研究了兩種格尼襟翼對不同實度的垂直軸風力機氣動性能的影響，并基于對比研究驗證計算模型的可靠性，分析具有GF 的VAWT 的風能利用系數、力矩系數和載荷波動在不同尖速比和不同實度下的數據。

1 空氣動力學模型與網格模型

1.1 格尼襟翼模型及改型

半圓形凹槽是一種可在大攻角下通過反旋渦流抑制流動分離的被動流動控制技術［26］。本文將格尼襟翼與半圓形凹槽相結合以期提升VAWT的氣動性能。為書寫簡潔，下文中改進型GF 在圖中均稱為dimple-GF。圖1 為基于NACA0021翼型的兩種GF 物理模型，圖中：GF 高度hG、厚度LG分別為c的1.25%、0.04%；半圓形凹槽直徑Dd與hG相等；尾緣與GF 間距SGT為c的10%。

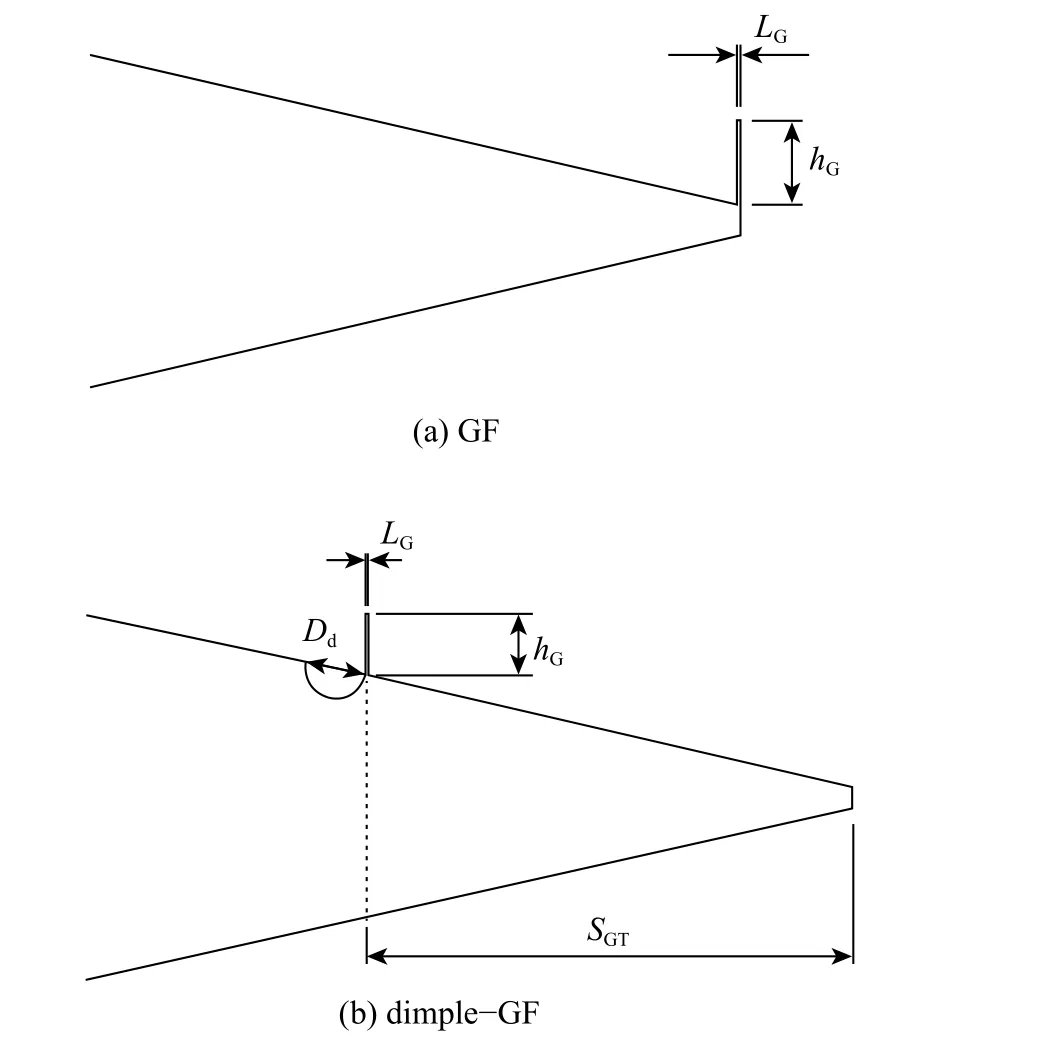
圖 1 GF、dimple-GF 物理模型Fig. 1 GF、dimple-GF physical model

圖2 為GF 翼型和改進型GF 翼型周圍的網格模型。第一層網格高度滿足第一層網格質心至壁面無量綱高度y+= 1，其網格最小正交質量分別為0.607 和0.528，網格最小畸變率分別為0.628和0.436。

1.2 垂直軸風力機模型

風能利用系數CP與 力矩系數Cm(θ)公式為

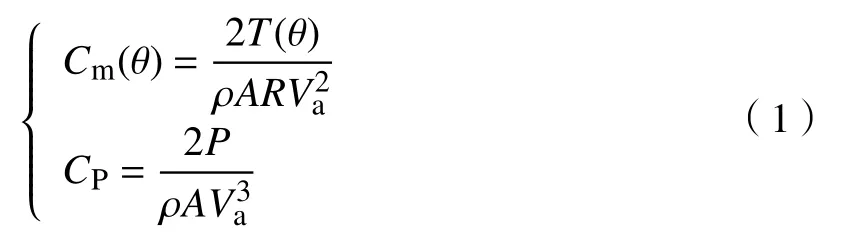
式中：T(θ)為 風力機在方位角 θ時所受的轉矩，N·m-1；P為輸出功率，W； ρ為空氣密度，kg·m-3；A為 掃 風 面 積，m2；Va為 誘 導 速 度，m·s-1；R為旋轉半徑，m。

實度 σ為設計參數，下文中風力機半徑保持不變。實度為0.175、0.250 對應葉片3（弦長分別為60.06 、85.80 mm），實度為0.333 對應葉片4（弦長與實度為0.250 對應葉片的一致），實度為0.416 對應葉片5，實度為0.500 對應葉片6。

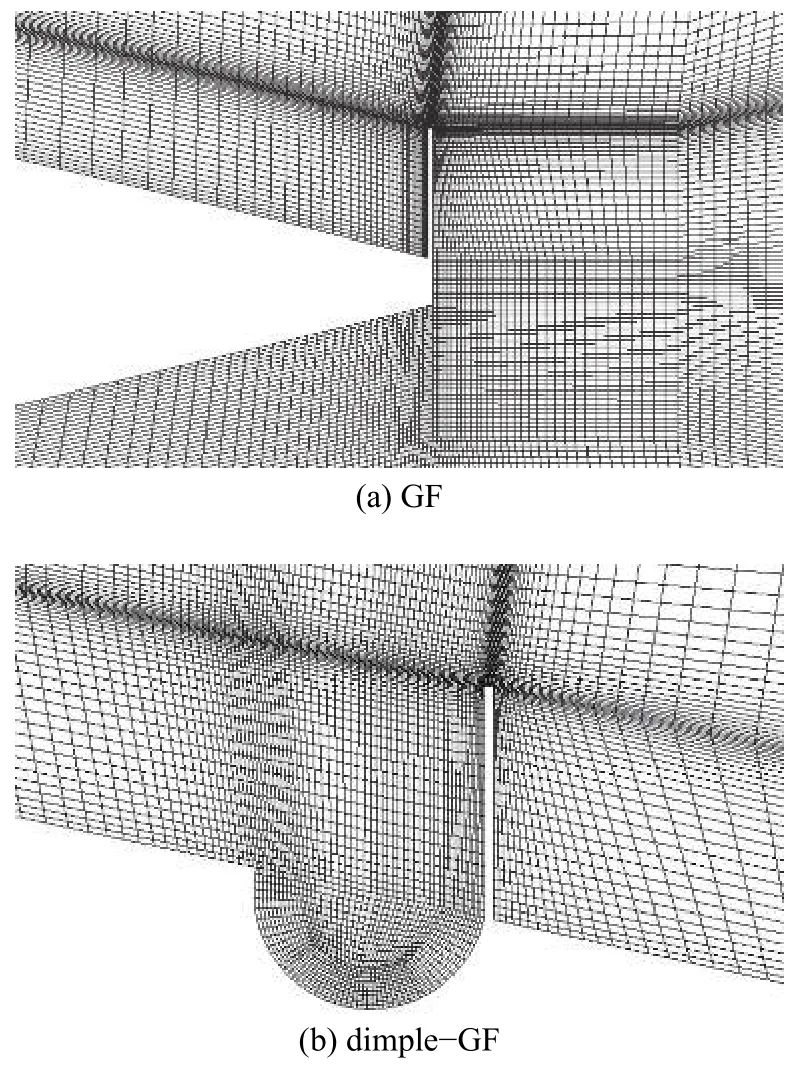
圖 2 GF、dimple-GF 網格模型Fig. 2 GF、dimple-GF mesh model

式中，N為葉片數。

尖速比λ 反映垂直軸風力機運行工況，即

式中： ω為角速度，rad·s-1；V∞為來流速度，m·s-1。

圖3、4 分別為VAWT 物理模型及拓撲結構，圖中W為相對速度。除Z2 區域外，其他區域（Z1、Z3）均為結構網格。原始VAWT、具有原始GF 的VAWT、具有改進型GF 的VAWT 的總網格數分別為509 222、619 394 和656 264。

圖 3 VAWT 物理模型Fig. 3 Physical model of VAWT

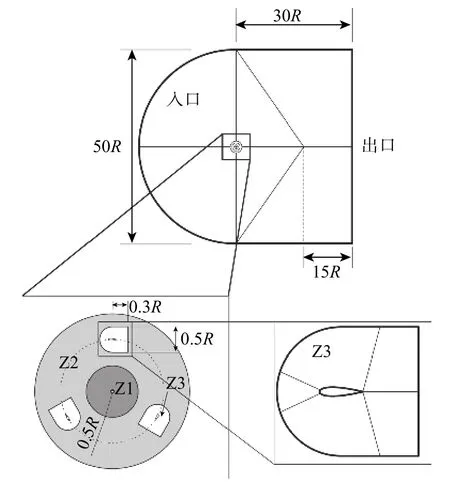
圖 4 VAWT 拓撲結構Fig. 4 Topological structure of VAWT

2 計算模型的可靠性驗證

2.1 數值算法及湍流模型

本文采用TSST 湍流模型。該湍流模型在捕捉層流至湍流的轉捩時具有較好的精度，且在垂直軸風力機周圍流場的數值計算中已廣泛使用［27-28］。本文算例中壁面y+均取1，并均基于弦長的雷諾數，網格尺寸變化比例為1.05～1.08。采用Simplec 算法并均采用二階迎風格式計算對流項，選用亞松弛因子以保證算法的收斂性。

2.2 邊界條件

入口邊界條件為速度入口，來流風速為9 m·s-1，入口湍流強度為3%，湍流黏性系數為1，空氣密度為1.225 kg·m-3，空氣動力黏度為1.789 4 ×10-5Pa·s，出口相對壓力為0 Pa。

2.3 計算模型可靠性驗證

本文選取展弦比為17 的SB-VAWT，通過獲得單位掃風面積的風能利用系數，確定原始SB-VAWT 的風能利用系數，并與實驗數據［29］進行對比。圖5 為計算模型可靠性對比，研 究Standardk-ε 、Realizablek-ε 、SSTk-ω和TSST 湍流模型的模擬值和實驗值的誤差，以驗證計算模型的可靠性。

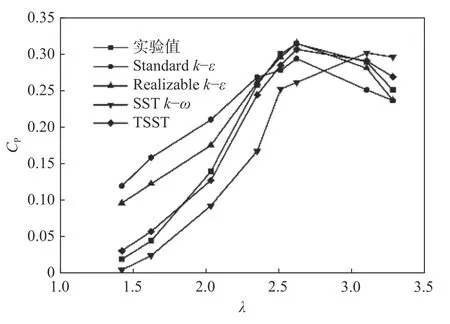
圖 5 計算模型可靠性對比Fig. 5 Comparative study on the reliability of the computational models

由圖5 中可知，TSST 湍流模型可較好地捕捉實驗值。相比其他假設流體為全湍的湍流模型，TSST 湍流模型可更精確地計算低尖速比下VAWT 的氣動性能。

本文采用網格收斂性索引（grid convergence index，GCI），建立基于具有改進型GF 垂直軸風力機的粗糙網格、中等精度網格和高精度網格模型，網格數分別為406 422、604 715 和901 254。圖6 為采用不同網格模型時葉片切向力隨方向角的變化。

由圖6 中可知，中等精度網格和高精度網格模型的計算結果接近，而粗糙網格葉片所受推力低于高精度網格，粗糙網格、中等精度網格和高精度網格對應的SB-VAWT 的風能利用系數分為0.303 1、0.307 4 和0.309 0，對應的網格收斂率為-2.438。若采用安全系數為1.25，以中等精度網格的計算結果作為中間變量，得到的高精度網格GCI 為8 .56×10-3，中等精度網格GCI 為3.18×10-3。可見，中等精度網格模型也具有較好的收斂性。

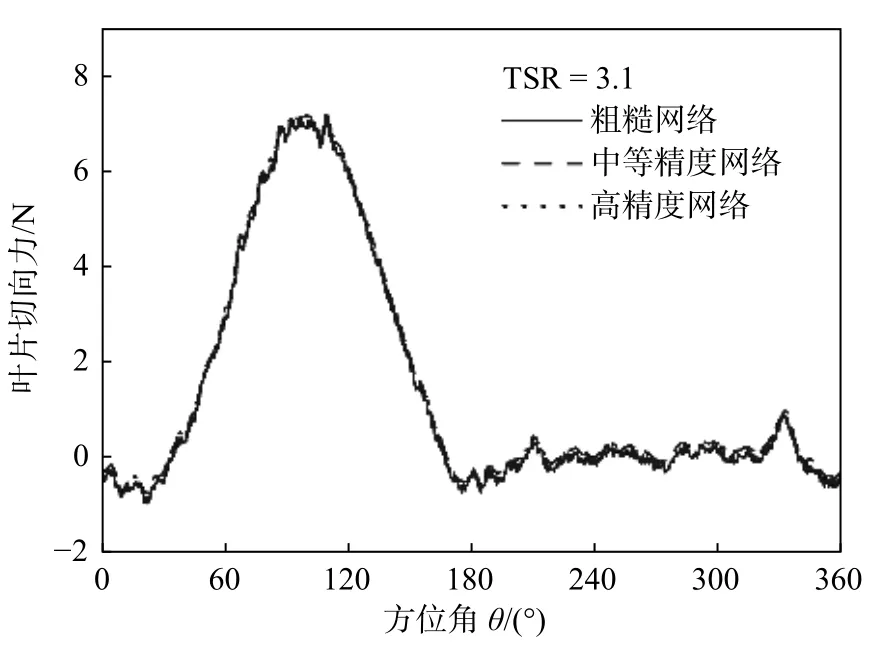
圖 6 在不同網格模型時葉片切向力隨方位角的變化Fig. 6 Variation of tangential force of a blade with azimuth angles for different mesh models

3 結果與分析

圖7 為具有兩種GF 的VAWT 氣動性能曲線，圖中Clean 為原始風力機。由圖7（a）～（e）中可發現，當尖速比為3.1、實度為0.250 時，原始格尼襟翼最大可提升10.92%的風能利用系數，改進型格尼襟翼最大可提升17.92%。在不同實度，改進型格尼襟翼在高尖速比時可較好地提升氣動性能，而原始格尼襟翼在低尖速比時可較好地提升氣動性能。

圖7（f）為VAWT 整機的力矩系數隨方位角變化的極曲線。由圖中可知，隨著實度的增加力矩系數曲線更趨近于類圓形，平均力矩系數越小，葉片平均受載均大于原始VAWT。

圖7（g）為力矩載荷波動隨尖速比的變化。由圖 7（g）中可知，當實度大于0.333 時，載荷波動大幅削弱。當尖速比增大時，波動程度趨于緩和。當尖速比減小時，由于葉片失速更為嚴重，故波動程度將更為劇烈。特別地，與實度為0.250 時相比，實度為0.175 時載荷波動情況較好，這是由于較小的葉片弦長承受更小的載荷且葉片間干擾削弱。

4 結 論

本文采用Fluent15.0 軟件進行數值模擬并分析得出GF 可大幅提升風力機氣動性能。主要結論為：

（1）GF 和改進型GF 均可大幅提升VAWT 的氣動性能，當尖速比為3.1、實度為0.25 時，原始GF 最大可提升10.92%的風能利用系數，改進型GF 最大可提升17.92%。改進型GF 更適用于高尖速比工況，而原始GF 適用于低尖速比工況。

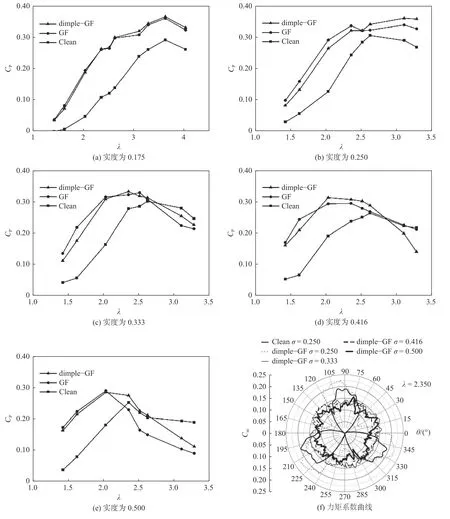
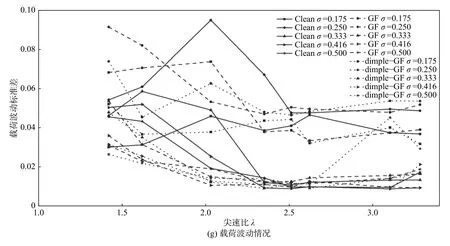
圖 7 具有GF 的VAWT 氣動性能Fig. 7 Aerodynamic performance of VAWT with GF

（2）隨著實度增大，由于葉片間干擾導致風能利用系數降低，但載荷波動情況得到改善。實度為0.416 時，載荷波動情況最優。

GF 與其他被動流動控制或主動流動控制相結合是格尼襟翼未來發展的重點。本文就原始GF 和改進型GF 在不同實度的垂直軸風力機中的應用展開了研究，為選擇較優的具有格尼襟翼的垂直軸風力機結構參數提供了參考。